Int. J. Communications, Network and System Sciences, 2009, 2, 827-835
doi:10.4236/ijcns.2009.29096 Published Online December 2009 (http://www.SciRP.org/journal/ijcns/).
827
Fuzzy Timed Agent Based Petri Nets for Modeling
Cooperative Multi-Robot Systems
Xingli HUANG, Hua XU, Peifa JIA
State Key Laboratory on Intelligent Technology and Systems, Tsinghua National Laboratory for
Information Science and Technology, Department of Computer Science and Technology,
Tsinghua University, Beijing, China
Received September 1, 2009; revised October 11, 2009; accepted November 20, 2009
Abstract
A cooperative multi-robot system (CMRS) modeling method called fuzzy timed agent based Petri nets
(FTAPN) is proposed in this paper, which has been extended from fuzzy timed object-oriented Petri net
(FTOPN). The proposed FTAPN can be used to model and illustrate both the structural and dynamic aspects
of CMRS, which is a typical multi-agent system (MAS). At the same time, supervised learning is supported
in FTAPN. As a special type of high-level object, agent is introduced into FTAPN, which is used as a com-
mon modeling object in its model. The proposed FTAPN can not only be used to model CMRS and represent
system aging effect, but also be refined into the object-oriented implementation easily. At the same time, it
can also be regarded as a conceptual and practical artificial intelligence (AI) tool for multi-agent systems
(MAS) into the mainstream practice of the software development.
Keywords: Petri nets, Multi Cooperative Robot Systems, Multi-Agent Systems
1. Introduction
As a kind of typical manufacturing equipment, coopera-
tive multi-robot systems (CMRS) have been widely used
in current industries [1]. The key solution for one CMRS
is to realize the cooperation, which is different from ge-
neric control systems. So, currently, the CMRS modeling,
analysis and refinement always meet with difficulties
related to the cooperation problem. As one of the typical
multi-agent systems (MAS) in distributed artificial intel-
ligence [2], CMRS can be regarded as one MAS. In or-
der to model MAS, some attempts to use object-oriented
methodology have been tried and some typical agent
objects have been proposed, such as active object, etc [3].
However, agent based object models still can not depict
the whole structure and dynamic aspects of MAS, such
as cooperation, learning, temporal constraints, etc [2].
On one hand, as one of the most proper and promised
realization technologies, object-oriented concurrent pro-
gramming (OOCP) methodology is always used to real-
ize MAS [3]. In OOCP realization, one special object
called active object is proposed [3], which can be used to
model generic agent architectures and behaviors with OO
methodology. Although OOCP can solve MAS realiza-
tion problem favorably, the modeling problem mentioned
above still exists.
On the other hand, as a kind of powerful formal de-
scription and analysis method for dynamic systems [4],
Petri net (PN) has become a bridge between practical
application and model theories [4]. Basic Petri nets lack
temporal knowledge description, so they have failed to
describe the temporal constraints in time critical or time
dependent systems. Then in the improved models of Petri
nets such as Timed (or Time) Petri nets (TPN) [5,6] etc
al, temporal knowledge has been introduced, which has
increased not only the modeling power but also the
model complexity [7]. On the other hand, when Petri nets
are used to analyze and model practical systems in dif-
ferent fields, models may be too complex to be analyzed.
These years, object-oriented concepts have been intro-
duced into Petri nets such as object Petri nets (OPN) [8],
VDM++ [9], Object-Z [10], etc al. are suggested. Among
the studies, the research on OPN has been focused on the
extending Petri net formalism to OPN such as HOONet
[11], OBJSA [12], COOPN/2 [13] and LOOPN++ [14],
which are suggested on the base of colored Petri Net
(CPN) [15]. Object-oriented Petri net (OPN) can model
various systems hierarchically and the models can be
analyzed even if they have not been completed. So the
complexity of OPN models can be simplified at the be-

X. L. HUANG ET AL. 828
ginning of modeling stage according to the analysis re-
quirements. Although the results of such studies have
shown promise, these nets do not fully support time
critical (time dependent) system modeling and analysis,
which may be complex, midsize or even small. When
time critical systems with any sizes are modeled, it re-
quires formal modeling and analysis method supporting
temporal description and object-oriented concepts. Then
for providing the ability of modeling time critical com-
plex systems, timed hierarchical object oriented Petri net
(TOPN) [16] is proposed on the base of HOONet [11]. It
supports temporal knowledge description and ob-
ject-oriented concepts. Modeling features in TOPN sup-
port describing and analyzing dynamic systems such as
MAS and CMRS. Recently, some attempts have been
conducted on modeling MAS by means of OPN [17].
Although Petri nets can be used to model and analyze
different systems, they failed to model learning ability
and the aging effects in dynamic systems. Recently,
fuzzy timed Petri net (FTPN) [18] has been presented to
solve these modeling problems. As a kind of reasoning
and learning ability, fuzzy reasoning in FTPN can be
considered as supporting autonomous judging or reason-
ing ability in MAS. In order to solve the reasoning ability
and other modeling problems in large-scale MAS, fuzzy
timed object-oriented Petri net (FTOPN) [19] is proposed
on the base of TOPN [16] and FTPN [18]. In FTOPN,
agent can be modeled as one FTOPN object with auto-
nomy, situatedness and sociality. However, in FTOPN
every agent should be modeled from common FTOPN
objects and it needs generic FTOPN agent objects on the
base of active objects.
This paper proposes a high level PN called fuzzy
timed agent based Petri net (FTAPN) on the base of
FTOPN [19]. As one of the typical active objects, AC-
TALK object is modeled by FTOPN and is introduced
into FTAPN, which is used as generic agent object in
FTAPN. The aim of FTAPN is to solve the agent or
CMRS modeling ability problem and construct a bridge
between MAS models and their implementations.
This paper is organized as the following. Section 2 re-
views the relative preliminary notations quickly and Sec-
tion 3 extends FTOPN to FTAPN on the base of AC-
TALK model. Section 4 discusses the learning which is
important for representing dynamic behaviors in CMRS.
Section 5 uses FTAPN to model one CMRS in the wafer
etching procedure of circuit industry and makes some
modeling analysis to demonstrate its benefits in model-
ing MAS. Finally, the conclusion and future work can be
found in Section 6.
2. Preliminary Notations
In this section, the basic concepts of ACTALK are firstly
reviewed, which is the relative concept in object-oriented
concurrent programming. Then, the definitions of TOPN
and FTOPN are introduced quickly, which are the basis
of the research work in this paper.
2.1. ACTALK
2.1.1. Active Objects [3]
Object-oriented concurrent programming (OOCP) is one
of the most appropriate and promising technologies for
implementing or realizing agent based systems or MAS.
Combining the agent concept and the object-oriented
paradigm leads to the notion of agent-oriented program-
ming [20]. The uniformity of objects’ communication
mechanisms provides facilities for implementing agent
communication, and the concept of encapsulating objects
or encapsulation support combining various agent gra-
nularities. Furthermore, the inheritance mechanism en-
ables knowledge specialization and factorization.
The concept of an active object has been presented,
which make it possible to integrate an object and activity
(namely a thread or process). It also provides some de-
gree of autonomy for objects in that it does not rely on
external resources for activation. Thus, it provides a
good basis for implementing agent based systems or
MAS. However, similar to common objects in ob-
ject-oriented systems, an active object’s behavior still
remains procedural and only reacts to message requests.
More generally, the main feature of agent-based systems
or MAS is autonomous. Agents should be able to com-
plete tasks autonomously. That’s to say, agents must be
able to perform numerous functions or activities without
external intervention over extended time periods. In or-
der to achieve autonomy, adding to an active object a
function that controls message reception and processing
by considering its internal state is one of the effective
realization methods [21,22].
On one hand, for modelling and realizing MAS, there
are two basic questions regarding how to build a bridge
between implementing and modelling MAS requirements
[23,24]. On the other hand, the facilities and techniques
OOCP provides [25]:
l How can a generic structure define an autonomous
agent’s main features?
l How do we accommodate the highly structured
OOCP model in this generic structure?
The active-object (or actor) concept has been intro-
duced to describe a set of entities that cooperate and
communicate through message passing. This concept
brings the benefits of object orientation (for example,
modularity and encapsulation) to distributed environ-
ments and provides object-oriented languages with some
of the characteristics of open systems [26]. Based on
these characteristics, various active object models have
been proposed [27], and to facilitate implementing ac-
tive-object systems, several frameworks have been pro-

X. L. HUANG ET AL. 829
posed. ACTALK is one example.
When ACTALK is used to model and realize the MAS,
there still exist the following shortcomings:
l Active object is not an autonomous agent. It only
manifests the procedural actions.
l Although active object can communicate, they do
not own the ability to reduce the decision to communi-
cate or order other active objects.
l If one active object has not received the information
from other active objects. It is still in none-active state.
In order to overcome the shortcomings mentioned
above, the concept of active object has been proposed
and a general agent framework [22,28]. A universal
agent architecture has also been proposed so as to fulfil
the modelling requirements of MAS [25], which can be
used to model and analyze MAS deeply. For either
agent-based systems or MAS, the method mostly is on
the base of active objects. So in this chapter, the concept
of active object is firstly reviewed quickly.
2.1.2. ACTALK [29]
One of the typical active objects is ACTALK. ACTALK
is a framework for implementing and computing various
active-object models into a single programming envi-
ronment based on Smalltalk, which is an object-oriented
programming language. ACTALK implements asyn-
chronism, a basic principle of active-object languages, by
queuing the received messages into a mailbox, thus dis-
sociating message reception from interpretation. In
ACTALK, an active object is composed of three com-
ponent classes (see Figure 1), which are instances of the
classes.
l Address encapsulates the active object’s mailbox. It
defines how to receive and queue messages for later in-
terpretation.
l Activity represents the active object’s internal ac-
tivity and provides autonomy to the actor. It has a
Smalltalk process and continuously removes messages
from the mailbox, and the behavior component interprets
the messages.
l ActiveObject represents the active object’s behav-
ior—that is, how individual messages are interpreted.
To build an active object with ACTALK, the algo-
rithm must describe its behavior as a standard Smalltalk
(OOCP) object. The active object using that behavior is
created by sending the message active to the behavior:
active
“Creates an active object with self as corresponding
behavior”
^self activity: self activityClass address: self address-
Class
The activityClass and addressClass methods represent
the default component classes for creating the activity
and address components (along the factory method de-
sign pattern). To configure the framework of ACTALK
means to define the components of its sub-classes. That’s
Figure 1. Components of an ACTALK active object.
to say, it allows users to define special active object mo-
dels. So ACTALK is the basis to model agent based sys-
tems or MAS.
2.2. Timed Object-Oriented Petri Net (TOPN)
Formally TOPN is a four-tuple (OIP, ION, DD, SI),
where (OIP, ION, DD) is an ordinary object Petri
net—“HOONet” [30] and SI associates a static (firing)
temporal interval SI: {o}→[a, b] with each object o,
where a and b are rationals in the range 0≤a≤b≤+∝,
with b≠+∝. The four parts in TOPN have different
function roles. Object identification place (OIP) is a
unique identifier of a class. Internal timed object net
(ION) is a net to depict the behaviors (methods) of a
class. Data dictionary (DD) declares the attributes of a
class in TOPN. And static time interval function (SI)
binds the temporal knowledge of a class in TOPN. There
are two kinds of places in TOPN. They are common
places (represented as circles with thin prim) and abstract
places (represented as circles with bold prim). Abstract
places are also associated with a static time interval. Be-
cause at this situation, abstract places represent not only
firing conditions, but also the objects with their own be-
haviors. So, abstract places (TABP) in TOPN also need
to be associated with time intervals. One problem to be
emphasized is that the tokens in abstract places need to
have two colors at least. Before the internal behaviors of
an abstract place object are fired, the color of tokens in it
is one color (represented as hollow token in this paper).
However, after fired, the color becomes the other one
Figure 2. The general structure of TOPN.

X. L. HUANG ET AL. 830
Figure 3. Places and transitions in TOPN.
(represented as liquid token in this paper). At this time,
for the following transitions, it is just actually enabled.
There are three kinds of transitions in TOPN. The timed
primitive transition (represented as rectangles with thin
prim) (TPIT), timed abstract transition (represented as
rectangles with bold prim) (TABT) and timed communi-
cation transition (represented as rectangles with double
thin prim) (TCOT).
Static time intervals change the behavior of TOPN just
similar to a time Petri net in the following way. If an
object o with SI(o) = [a, b] becomes enabled at time I0,
then the object o must be fired in the time interval [I0+a,
I0+b], unless it becomes disabled by the removal of to-
kens from some input place in the meantime. The static
earliest firing time of the object o is a; the static latest
firing time of o is b; the dynamic earliest firing time
(EFT) of t is I0+a; the dynamic latest firing time (LFT) of
t is I0+b; the dynamic firing interval of t is [I0+a, I0+b].
The state of TOPN (Extended States—“ES”) is a 3-
tuple, where ES = (M, I, path) consists of a marking M, a
firing interval vector I and an execution path. According
to the initial marking M0 and the firing rules mentioned
above, the following marking at any time can be calcu-
lated. The vector—“I” is composed of the temporal in-
tervals of enabled transitions and TABPs, which are to
be fired in the following states. The dimension of I
equals to the number of enabled transitions and TABPs
at the current state. The firing interval of every enabled
transition or TABP can be got according to the calcula-
tion formula of EFT and LFT in TOPN [16].
For enabling rules in TOPN, two different situations
exist. A transition t in TOPN is said to be enabled at the
current state (M, I, path), if each input place p of t con-
tains at least the number of solid tokens equal to the
weight of the directed arcs connecting p to t in the mark-
ing M. If the TABP object is marked with a hollow token,
it is enabled. At this time, its ION is enabled. After the
ION has been fired, the tokens in TABP are changed into
solid ones.
An object o is said to be fireable in state (M, I, path) if
it is enabled, and if it is legal to fire o next. This will be
true if and only if the EFT of o is less than or equal to the
LFT of all other enabled transitions. Of course, even with
strong time semantics, o’s being fireable in state (M, I,
path) does not necessarily mean that t will fire in the time
interval I.
2.3. Fuzzy Timed Object-Oriented Petri Net
(FTOPN)
Similar to FTPN [19], fuzzy set concepts are introduced
into TOPN [16]. Then FTOPN is proposed, which can
describe fuzzy timing effect in dynamic systems.
Definition 1: FTOPN is a six-tuple, FTOPN = (OIP,
ION, DD, SI, R, I) where
1) Suppose OIP = (oip, pid, M0, status), where oip, pid,
M0 and status are the same as those in HOONet [30] and
TOPN [16].
l oip is a variable for the unique name of a FTOPN.
l pid is a unique process identifier to distinguish mul-
tiple instances of a class, which contains return address.
l M0 is the function that gives initial token distribu-
tions of this specific value to OIP.
l status is a flag variable to specify the state of OIP.
2) ION is the internal net structure of FTOPN to be
defined in the following. It is a variant CPN that de-
scribes the changes in the values of attributes and the
behaviors of methods in FTOPN.
3) DD formally defines the variables, token types and
functions (methods) just like those in HOONet [30] and
TOPN [16].
4) SI is a static time interval binding function, SI:
{OIP}→Q*, where Q* is a set of time intervals.
5) R: {OIP} → r, where r is a specific threshold.
6) I is a function of the time v. It evaluates the result-
ing degree of the abstract object firing.
Definition 2: An internal object net structure of TOPN,
ION = (P, T, A, K, N, G, E, F, M0)
1) P and T are finite sets of places and transitions with
time restricting conditions attached respectively.
2) A is a finite set of arcs such that P∩T = P∩A =
T∩A = Φ.
3) K is a function mapping from P to a set of token
types declared in DD.
4) N, G, and E mean the functions of nodes, guards,
and arc expressions, respectively. The results of these
functions are the additional condition to restrict the firing
of transitions. So they are also called additional restrict-
ing conditions.
5) F is a special arc from any transitions to OIP, and
notated as a body frame of ION.
6) M
0
is a function giving an initial marking to any
place the same as those in HOONet [30] and TOPN [16].
Definition 3: A set of places in TOPN is defined as P

X. L. HUANG ET AL. 831
= PIP∪TABP, where
1) Primary place PIP is a three-tuple: PIP = (P, R, I),
where
l P is the set of common places similar to those in PN
[4,31].
2) Timed abstract place (TABP) is a six-tuple: TABP
= TABP(pn, refine state, action, SI, R, I), where
l pn is the identifier of the abstract timed place.
l refine state is a flag variable denoting whether this
abstract place has been refined or not.
l action is the static reaction imitating the internal
behavior of this abstract place.
l SI, R and I are the same as those in Definition 1.
Definition 4: A set of transitions in TOPN can be de-
fined as T = TPIT∪TABT∪TCOT, where
1) Timed primitive transition TPIT = TPIT (BAT, SI),
where
l BAT is the set of common transitions.
2) Timed abstract transition TABT = TABT (tn, refine
state, action, SI), where
l tn is the name of this TABT.
3) Timed communication transition TCOT = TCOT
(tn, target, comm type, action, SI).
l tn is the name of TCOT.
l target is a flag variable denoting whether the be-
havior of this TCOT has been modeled or not. If target =
“Yes”, it has been modeled. Otherwise, if target = “No”,
it has not been modeled yet.
l comm type is a flag variable denoting the commu-
nication type. If comm type = “SYNC”, then the com-
munication transition is synchronous one. Otherwise, if
comm type = “ASYN”, it is an asynchronous communi-
cation transition.
4) SI is the same as that in Definition 1.
5) Refine state and action are the same as those in De-
finition 3.
Similar to those in FTPN [19], the object t fires if the
foregoing objects come with a nonzero marking of the
tokens; the level of firing is inherently continuous. The
level of firing (z(v)) assuming values in the unit interval
is governed by the following expression:
)()))((()( 1vtswvxrTvz iii
n
iΙ
′
→= = (1)
where T (or t) denotes a t-norm while “s” stands for any
s-norm. “v” is the time instant immediately following v′.
More specifically, xi(v) denotes a level of marking of the
ith place. The weight w
i
is used to quantify an input
coming from the ith place. The threshold ri expresses an
extent to which the corresponding place’s marking con-
tributes to the firing of the transition. The implication
operator (→) expresses a requirement that a transition
fires if the level of tokens exceeds a specific threshold
(quantified here by ri).
Once the transition has been fired, the input places
involved in this firing modify their markings that is
governed by the expression
xi(v) = xi(v′)t(1−z(v)) (2)
(Note that the reduction in the level of marking de-
pends upon the intensity of the firing of the correspond-
ing transition, z(v).) Owing to the t-norm being used in
the above expression, the marking of the input place gets
lowered. The output place increases its level of tokens
following the expression:
y(v) = y(v′)sz(v) (3)
The s-norm is used to aggregate the level of firing of
the transition with the actual level of tokens at this output
place. This way of aggregation makes the marking of the
output place increase.
The FTOPN model directly generalizes the Boolean
case of TOPN and OPN. In other words, if xi(v) and wi
assume values in {0, 1} then the rules governing the be-
havior of the net are the same as those encountered in
TOPN.
3. Agent Objects and Fuzzy Timed Agent
Based Petri Nets
The active object concept [29] has been proposed to de-
scribe a set of entities that cooperate and communicate
through message passing. To facilitate implementing
active object systems, several frameworks have been
proposed. ACTALK is one of the typical examples.
ACTALK is a framework for implementing and com-
puting various active object models into one object-ori-
ented language realization. ACTALK implements asyn-
chronism, a basic principle of active object languages, by
queuing the received messages into a mailbox, thus dis-
sociating message reception from interpretation. In ACTALK,
Figure 4. The FTOPN model of ACTALK.

X. L. HUANG ET AL. 832
an active object is composed of three component classes:
address, activity and activeObject [29].
ACTALK model is the basis of constructing active
object models. However, active object model is the basis
of constructing multi-agent system model or agent-based
system model. So, as the modeling basis, ACTALK has
been extended to different kinds of high-level agent
models. Because of this, ACTALK is modeled in Fig.4
by FTOPN.
In Figure 4, OIP is the describer of the ACTALK
model and also represents as the communication address.
One communication transition is used to represent as the
behavior of message reception. According to the com-
munication requirements, it may be synchronous or
asynchronous. If the message has been received, it will
be stored in the corresponding mail box, which is one
“first in and first out queue”. If the message has been
received, the next transition will be enabled immediately.
So mail box is modeled as abstract place object in
FTAPN. If there are messages in the mail box, the fol-
lowing transition will be enabled and fired. After the
following responding activity completes, some active
behavior will be conducted according to the message.
Figure 4 has described the ACTALK model based on
FTOPN on the macroscopical level. The detailed defini-
tion or realization of the object “Activity” and “Behav-
ior” can be defined by FTOPN in its parent objects in the
lower level. The FTOPN model of ACTALK can be used
as the basic agent object to model agent based systems.
That is to say, if the agent based model—ACTALK
model is used in the usual FTOPN modeling procedure,
FTOPN has been extended to agent based modeling
methodology. So it is called fuzzy timed agent based
Petri net (FTAPN).
4. Learning in Fuzzy Timed Agent Based
Petri Nets
The parameters of FTAPN are always given beforehand.
In general, however, these parameters may not be avail-
able and need to be estimated just like those in FTPN
[19]. The estimation is conducted on the base of some
experimental data concerning marking of input and out-
put places. The marking of the places is provided as a
discrete time series. More specifically we consider that
the marking of the output place(s) is treated as a collec-
tion of target values to be followed during the training
process. As a matter of fact, the learning is carried out in
a supervised mode returning to these target data.
The connections of the FTOPN (namely weights w
i
and thresholds ri) as well as the time decay factors αi are
optimized (or trained) so that a given performance index
Q becomes minimized. The training data set consists of
(a) initial marking of the input places xi(0),… , xn(0) and
(b) target values—markings of the output place that are
given in a sequence of discrete time moments, that is
target(0), target(1),…, target(K).
In FTAPN, the performance index Q under discussion
assumes the form of Equation (4)
Q = ∑
=
−
K
k
kykett
1
2
))()(arg( (4)
where the summation is taken over all time instants (k =1,
2,… , K).
The crux of the training in FTOPN models follows the
general update formula in Equation (5) being applied to
the parameters:
param(iter+1) = param(iter) − γ∇paramQ (5)
where γ is a learning rate and ∇paramQ denotes a gradient
of the performance index taken with respect to all pa-
rameters of the net (here we use a notation param to
embrace all parameters in FTOPN to be trained).
In the training of FTOPN models, marking of the input
places is updated according to Equation (6):
)()0(
~kTxxiii = (6)
where T
i
(k) is the temporal decay. And T
i
(k) complies
with the form in Equation (7). In what follows, the tem-
poral decay is modeled by an exponential function,


>−−
=others
kkifkk
kT iii
i0
,))(exp(
)( α (7)
The level of firing of the place can be computed as
Equation (8):
~
1
((()))
n
iii
i
zTrxsw
=
=→ (8)
The successive level of tokens at the output place and
input places can be calculated as that in Equation (9):
y(k) = y(k−1)sz, xi(k) = xi(k−1)t(1−z) (9)
We assume that the initial marking of the output place
y(0) is equal to zero, y(0) = 0. The derivatives of the
weights wi are computed as the form in Equation (9):
2
(arg()())
()
2(arg()())
i
i
tetkyk
w
yk
tetkyk
w
∂−
∂
∂
=−−
∂
(10)
where i =1,2,…, n. Note that y(k+1) = y(k)sz(k).
5. A Modeling Example
5.1. A CMRS Model
In many typical integrated circuit manufacturing equip-
ments such as etching tools, PVD, PECVD etc al., usu-
ally there is an EFAM platform which is made up of
three Brooks Marathon Express (MX) [32] robots to
transfer wafers to be processed. Among these three robots,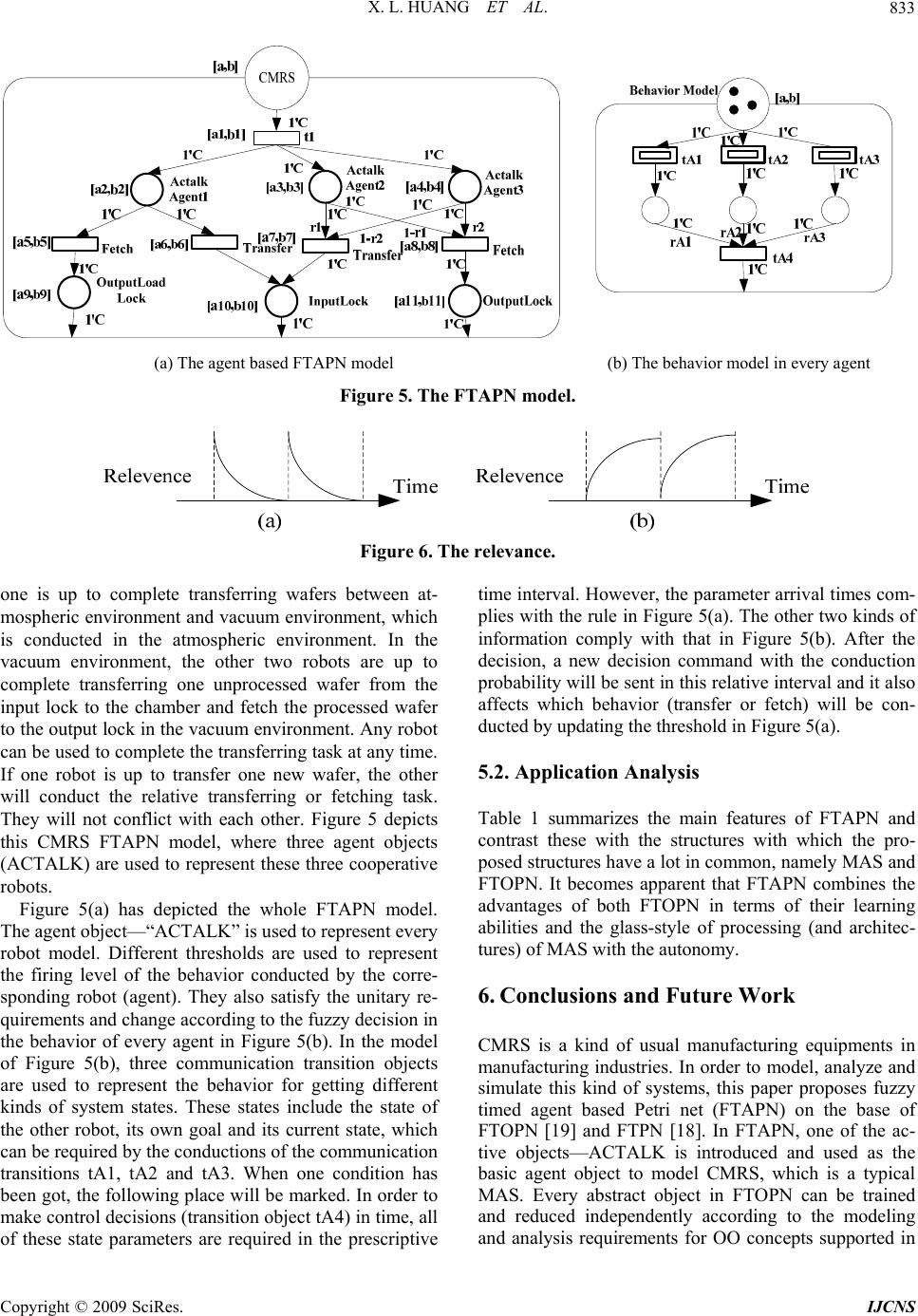

X. L. HUANG ET AL. 833
(a) The agent based FTAPN model (b) The behavior model in every agent
Figure 5. The FTAPN model.
Figure 6. The relevance.
one is up to complete transferring wafers between at-
mospheric environment and vacuum environment, which
is conducted in the atmospheric environment. In the
vacuum environment, the other two robots are up to
complete transferring one unprocessed wafer from the
input lock to the chamber and fetch the processed wafer
to the output lock in the vacuum environment. Any robot
can be used to complete the transferring task at any time.
If one robot is up to transfer one new wafer, the other
will conduct the relative transferring or fetching task.
They will not conflict with each other. Figure 5 depicts
this CMRS FTAPN model, where three agent objects
(ACTALK) are used to represent these three cooperative
robots.
Figure 5(a) has depicted the whole FTAPN model.
The agent object—“ACTALK” is used to represent every
robot model. Different thresholds are used to represent
the firing level of the behavior conducted by the corre-
sponding robot (agent). They also satisfy the unitary re-
quirements and change according to the fuzzy decision in
the behavior of every agent in Figure 5(b). In the model
of Figure 5(b), three communication transition objects
are used to represent the behavior for getting different
kinds of system states. These states include the state of
the other robot, its own goal and its current state, which
can be required by the conductions of the communication
transitions tA1, tA2 and tA3. When one condition has
been got, the following place will be marked. In order to
make control decisions (transition object tA4) in time, all
of these state parameters are required in the prescriptive
time interval. However, the parameter arrival times com-
plies with the rule in Figure 5(a). The other two kinds of
information comply with that in Figure 5(b). After the
decision, a new decision command with the conduction
probability will be sent in this relative interval and it also
affects which behavior (transfer or fetch) will be con-
ducted by updating the threshold in Figure 5(a).
5.2. Application Analysis
Table 1 summarizes the main features of FTAPN and
contrast these with the structures with which the pro-
posed structures have a lot in common, namely MAS and
FTOPN. It becomes apparent that FTAPN combines the
advantages of both FTOPN in terms of their learning
abilities and the glass-style of processing (and architec-
tures) of MAS with the autonomy.
6. Conclusions and Future Work
CMRS is a kind of usual manufacturing equipments in
manufacturing industries. In order to model, analyze and
simulate this kind of systems, this paper proposes fuzzy
timed agent based Petri net (FTAPN) on the base of
FTOPN [19] and FTPN [18]. In FTAPN, one of the ac-
tive objects—ACTALK is introduced and used as the
basic agent object to model CMRS, which is a typical
MAS. Every abstract object in FTOPN can be trained
and reduced independently according to the modeling
and analysis requirements for OO concepts supported in

X. L. HUANG ET AL. 834
Table 1. MAS, FTOPN and FTAPN: A comparative analysis.
Characteristics MAS FTOPN FTAPN
Learning Aspects
Significant dynamic learn-
ing abilities. Dynamic learn-
ing and decision abilities are
supported in every autono-
mous agent.
Significant learning abilities.
Distributed learning (training)
abilities are supported in dif-
ferent independent objects on
various system model levels.
Significant dynamic learning abilities.
Distributed dynamic learning and deci-
sion abilities are supported in every
autonomous agent.
Knowledge Repre-
sentation Aspects
Transparent knowledge re-
presentation (glass box proc-
essing style) the problem (its
specification) is mapped di-
rectly onto the topology of the
agent model. Additionally,
agents deliver an essential
feature of continuity required
to cope with dynamic changes
encountered in a vast array of
problems (including autono-
mous decision tasks)
Glass Box Style (Transpar-
ent Knowledge Representation)
and Black Box Processing is
supported at the same time. The
problem (its specification) is
mapped directly onto the to-
pology of FTOPN. Knowledge
representation granularity re-
configuration reacts on the
reduction of model size and
complexity.
Glass Box Processing Style and Black
Box Processing style are all supported.
The problem (its specification) is
mapped directly onto the topology of
FTAPN, which can not only represent
dynamic knowledge, but also deal with
dynamic changes with well-defined
semantics of agent objects, places, tran-
sitions, fuzzy and temporal knowledge.
FTOPN. The validity of this modeling method has been
used to model Brooks CMRS platform in etching tools.
The FTAPN can not only model complex MAS, but also
be refined into the object-oriented implementation easily.
It has provided a methodology to overcome the devel-
opment problems in agent-oriented software engineering.
At the same time, it can also be regarded as a conceptual
and practical artificial intelligence (AI) tool for integrat-
ing MAS into the mainstream practice of software de-
velopment.
State analysis needs to be studied in the future. An ex-
tended State Graph [16] has been proposed to analyze the
state change of TOPN models. With the temporal fuzzy
sets introduced into FTAPN, the certainty factor about
object firing (state changing) needs to be considered in
the state analysis.
7. Acknowledgement
This work is jointly supported by the National Nature
Science Foundation of China (Grant No: 60405011,
60575057, 60875073) and National Key Technology
R&D Program of China (Grant No: 2009- BAG12A08).
8. References
[1] Y. U. Cao, A. S. Fukunaga, A. B. Kahng, and F. Meng,
“Cooperative mobile robotics: Antecedents and direc-
tions,” Autonomous Robots, Vol. 4, pp. 7–27, 1997.
[2] N. R. Jennings, K. Sycara, and M. Wooldridge, “A road-
map of agent research and development,” Autonomous
Agents and Multi-Agent Systems, Vol. 1, pp. 7–38, 1998.
[3] Z. Guessoum and J. P. Briot, “From active objects to
autonomous agents,” IEEE Concurrency, Vol. 7, No. 3,
pp. 68–76, July–September 1999.
[4] T. Murata, “Petri nets and properties, analysis and appli-
cations,” Proceedings of IEEE, Vol. 77, pp. 541–580,
1989.
[5] Y. L. Yao, “A Petri net model for temporal knowledge
representation and reasoning,” IEEE Transactions on
Systems, Man and Cybernetics, Vol. 24, pp. 1374–1382,
1994.
[6] P. Merlin and D. Farber, “Recoverability of communica-
tion protocols—Implication of a theoretical study,” IEEE
Transactions on Communication, Vol. 24, pp. 1036–1043,
1976.
[7] J. Wang, Y. Deng, and M. Zhou, “Compositional time
Petri nets and reduction rules,” IEEE Transactions on
Systems, Man and Cybernetics (Part B), Vol. 30, pp.
562–572, 2000.
[8] R. Bastide, “Approaches in unifying Petri nets and the
object-oriented approach,” Proceeding of the Interna-
tional Workshop on Object-Oriented Programming and
Models of Concurrency, Turin, Italy, June, 1995, http://
eprints. kfupm.edu.sa/26256/.
[9] D. Harel and E. Gery, “Executable object modeling with
statechart,” Proceedings of the 18th International Con-
ference on Software Engineering, Germany, pp. 246–257,
March 1996.
[10] S. A. Schuman, “Formal object-oriented development,”
Springer, Berlin, 1997.
[11] J. E. Hong and D. H. Bae, “Software modeling and analy-
sis using a hierarchical object-oriented Petri net,” Infor-
mation Sciences, Vol.130, pp. 133–164, 2000.
[12] E. Battiston, F. D. Cindio, and G. Mauri, “OBJSA nets: A
class of high-level nets having objects as domains,”
APN’88, Lecture Notes in Computer Science, Vol. 340,
pp. 20–43, 1988.

X. L. HUANG ET AL. 835
[13] O. Biberstein and D. Buchs, “An object-oriented specifi-
cation language based on hierarchical algebraic Petri
nets,” Proceedings of the IS-CORE Workshop Amster-
dam, September 1994, http://citeseerx.ist.psu.edu/view-
doc/summary?doi=10.1.1.45.3092.
[14] C. Lakos and C. Keen, “LOOPN++: A new language for
object-oriented Petri nets,” Technical Report R94-4, Net-
working Research Group, University of Tasmania, Aus-
tralia, April 1994.
[15] K. Jensen, “Coloured Petri nets: Basic concepts, analysis
methods and practical use,” Springer, Berlin, 1992.
[16] H. Xu and P. F. Jia, “Timed hierarchical object-oriented
Petri net-part I: Basic concepts and reachability analysis,”
Lecture Notes in Artificial Intelligence (Proceedings of
RSKT2006), Vol. 4062, pp. 727–734, 2006.
[17] W. Chainbi, “Multi-agent systems: A Petri net with ob-
jects based approach,” Proceedings of IEEE/WIC/ACM
International Conference on Intelligent Agent Technol-
ogy, Beijing, pp. 429–432, 2004.
[18] W. Pedrycz and H. Camargo, “Fuzzy timed Petri nets,
fuzzy sets and systems,” Vol. 140, pp. 301–330, 2003.
[19] X. Hua and J. Peifa, “Fuzzy timed object-oriented Petri
net,” Artificial Intelligence Applications and Innovations
II-Proceedings of AIAI2005, Springer, pp. 155–166,
September 2005.
[20] Y. Shoham, “Agent-oriented programming,” Artificial In-
telligence, Vol. 60, No.1, pp. 139–159, 1993.
[21] J. P. Briot, “An experiment in classification and spe-
cialization of synchronization schemes,“ Lecture Notes in
Computer Science, No. 1107, pp. 227–249, 1996.
[22] T. Maruichi, M. Ichikawa, and M. Tokoro, “Decentralized
AI,” Modeling Autonomous Agents and Their Groups,
Elsevier Science, Amsterdam, pp. 215–134, 1990.
[23] C. Castelfranchi, “A point missed in multi-agent, DAI and
HCI,” Lecture Notes in Artificial Intelligence, No. 890,
pp. 49–62. 1995.
[24] L. Gasser, ”An overview of DAI, ” Distributed Artificial
Intelligence, N. A. Avouris and L. Gasser, eds., Kluwer
Academic, Boston, pp. 1–25, 1992.
[25] L. Gasser and J. P. Briot, ”Object-oriented concurrent
programming and distributed artificial intelligence,” Dis-
tributed Artificial Intelligence, N. A. Avouris and L.
Gasser, eds., Kluwer Academic, Boston, pp. 81–108,
1992.
[26] G. Agha and C. Hewitt, “Concurrent programming using
actors: Exploiting large scale parallelism,” Lecture Notes
in Computer Science, S. N. Maheshwari, ed., Springer-
Verlag, New York, No. 206, pp. 19–41, 1985.
[27] A. Yonezawa and M. Tokoro, “Object-oriented con-
current programming,” The MIT Press, Cambrige, Mass.,
1987.
[28] Y. Shoham, “Agent-oriented programming,” Artificial In-
telligence, Vol. 60, No.1, pp. 139–159, 1993.
[29] Z. Guessoum and J. P. Briot, “From active objects to
autonomous agents,” IEEE Concurrency, Vol. 7, No. 3,
pp. 67–76, 1999.
[30] J. E. Hong and D. H. Bae, ”Software modelling and
analysis using a hierarchical object-oriented Petri net,”
Information Sciences, Vol. 130, pp. 133–164, 2000.
[31] J. L. Peterson, “Petri net theory and the modeling of
systems,” Prentice-Hall, N.Y., USA, 1991.
[32] J. H. Lee and T. E. Lee, “SECAM: A supervisory equip-
ment control application model for integrated semi-
conductor manufacturing equipment, ” IEEE Robotics &
Automation Magazine, Vol. 11, No. 1, pp. 41 – 58, 2004..