A Mobile-Agent-Based Adaptive Data Fusion Algorithm for Multiple Signal Ensembles in Wireless Sensor Networks

doi:10.4236/wsn.2009.15055

Paper Menu >>

Journal Menu >>

Wireless Sensor Network, 2009, 1, 458-466

doi:10.4236/wsn.2009.15055 Published Online December 2009 (http://www.scirp.org/journal/wsn).

A Mobile-Agent-Based Adaptive Data Fusion Algorithm

for Multiple Signal Ensembles in

Wireless Sensor Networks

Tianjing WANG1, Zhen YANG2, Guoqing LIU1

College of Science, Nanjing University of Technology, Nanjing, China

2Institute of Signal and Information Processing, Nanjing University of Posts&Telecommunications, Nanjing, China

Email: tjingwang@126.com

Received June 8, 2009; revised August 17, 2009; accepted August 18, 2009

Abstract

Distributed Compressed Sensing (DCS) is an emerging field that exploits both intra- and inter-signal correla-

tion structures and enables new distributed coding algorithms for multiple signal ensembles in wireless sen-

sor networks. The DCS theory rests on the joint sparsity of a multi-signal ensemble. In this paper we propose

a new mobile-agent-based Adaptive Data Fusion (ADF) algorithm to determine the minimum number of

measurements each node required for perfectly joint reconstruction of multiple signal ensembles. We theo-

retically show that ADF provides the optimal strategy with as minimum total number of measurements as

possible and hence reduces communication cost and network load. Simulation results indicate that ADF en-

joys better performance than DCS and mobile-agent-based full data fusion algorithm including reconstruc-

tion performance and network energy efficiency.

Keywords: Wireless Sensor Networks, Mobile Agent, Compressed Sensing, Distributed Compressed Sensing,

Joint Sparsity, Joint Reconstruction

1. Introduction

Wireless Sensor Networks (WSN) are an emerging

technology that promises an ability to monitor the

physical world via spatially distributed networks of small

and inexpensive wireless sensor nodes that have the abil-

ity to self-organize into a well-connected network. The

communication tasks consume the limited power avail-

able at such sensor nodes and, therefore, in order to en-

sure their sustained operations, the power consumption

must be kept to minimum. Different from transmission

cost, the computational cost may be negligible for some

applications. For example, WSN monitoring field tem-

perature may use simple functions which essentially are

of insignificant cost. Consequently, a major challenge in

the design of WSN is developing schemes that extract

relevant information about the sensor data with the

minimum energy consumption, especially with transmis-

sion cost. In order to reduce transmission of sensor data,

a new framework for single signal sensing and compres-

sion has developed recently under the rubric of Com-

pressed Sensing (CS) [1–3]. The implications of CS are

promising for many applications, especially sensing sig-

nals that have a sparse representation in some basis [4–6].

Based on the intra-signal correlations (between samples

in each signal), CS can perfectly reconstruct a com-

pressible signal from remarkably few linear measure-

ments. In WSN, however, a large number of sensor

nodes presumably observe related phenomena and are

programmed to perform a variety of signals acquisition

tasks. These signals have high correlations and need to

be jointly processed, so the independently encoding and

decoding theory and practice of single signal in a CS

framework can not satisfy such applications. Fortunately,

the ensemble of signals that sensor nodes acquired can be

expected to possess some joint structure, or inter-signal

correlations (between samples across signals), in addition

to the intra-signal correlation of single signal. Most ex-

isting coding algorithms [7,8], however, exploit only

inter-signal correlations and not intra-signal correlations.

A new Distributed Compressed Sensing (DCS) theory

exploits both intra-signal and inter-signal correlation

structures of multiple signal ensembles [9–11]. In a typi-

cal DCS scenario, each individual node independently

encodes its signal by CS framework and then transmits

*Supported by the Young Teacher Academic Fund of Nanjing Univer-

sity of Technology

T. J. WANG ET AL.

459

the measurements to a distant Sink node (Sink) by multi-

ple skips. Under the right conditions, Sink can jointly

reconstruct multiple signal ensembles precisely. How-

ever, we note that the network traffic may be extremely

heavy in DCS, resulting in poor performance of the sys-

tem, when the number of sensor nodes is big and the

amount of sensing signals is large. Furthermore, nodes

can not know the suited minimum number of measure-

ments that they need to transmit to Sink under DCS

framework. In order to guarantee perfect reconstruction,

each node has to transmit enough measurements. This

means that DCS only utilizes the inter-signal correlations

in jointly decoding processes, but not in jointly encoding

processes.

In this paper, we design a mobile-agent-based Adap-

tive Data Fusion (ADF) algorithm for multiple signal

ensembles which is inspired by DCS. Instead of passing

large amounts of independently encoding measurements

by DCS in each individual node over the network, Mo-

bile Agent (MA) can fuse multiple signals from node to

node along a shortest path, based on Global Closest First

(GCF) heuristics algorithm [12]. According to the sparse

property of single signal and the joint sparsity of multiple

signal ensembles under the results of data fusion, each

node can determine the minimum number of measure-

ments needed to transmit to Sink and effectively reduces

the transmission cost. Extensive experiments in session 4

demonstrate that the energy efficiency and the recon-

struction performance of ADF are more excellent than

DSC and mobile-agent-based Full Data Fusion (FDF)

algorithm.

The organization of this paper is as follows. Section 2

overviews a joint sparsity model in DCS. Single signal

and multiple signals reconstruction methods are dis-

cussed respectively. Section 3 introduces our two mo-

bile-agent-based data fusion algorithms: Full Data Fu-

sion (FDF) and Adaptive Data Fusion (ADF). Detailed

theoretical analyses indicate that FDF and ADF are more

energy efficient than DCS, sufficiently utilizing intra-

signal and inter-signal correlation of multiple signal en-

sembles. Experiments in Section 4 confirm that ADF

indeed reduces large amounts of total transmission cost

and the number of total measurements compared to DCS

and FDF. Section 5 describes conclusions.

2. Distributed Compressed Sensing

2.1. Joint Sparsity Model

The recently introduced theory of DCS enables a new

distributed coding algorithm that exploits both intra- and

inter-signal correlation structures of multiple signals [9].

In this paper, we focus on a Joint Sparsity Models (JSM,

sparse common component +innovations), which can be

improved by mobile-agent-based data fusion. For exam-

ple, a practical situation well-modeled by the JSM is a

group of sensors {Sl

,…SJ

} measuring temperatures at a

number of outdoor locations throughout the day. The

temperature readings xl(l∈{1,2,…J}) have both tempo-

ral (intra-signal) and spatial (inter-signal) correlations.

Global factors, such as the sun and prevailing winds,

could have an effect that is both common to all sensors

and structured enough to permit sparse representation in

some basis. More local factors, such as shade, water, or

animals, could contribute localized innovations that are

also structured (and hence sparse in some basis). A simi-

lar scenario could be imagined for a network of sensors

recording light intensities, air pressure, or other phe-

nomena. All of these scenarios correspond to measuring

properties of physical processes that change smoothly in

time and in space and thus are highly correlated.

We adopt language and notation from [9]. Assume that

there exists a known basis

{|,1,,}

Rim

ψψΨ=∈=

which a signal

{(1),,()}({1,2,,})

lll

xxxmRlJ

=∈∈

can be sparsely represented as

=Ψ

, where

((1),,())

lll

mθθθ=

is a sparse coefficient vector and

||||

. Thus, a compressible multiple signal ensem-

ble 1

shares a common sparse component while

each single signal contains an innovation sparse compo-

nent. That is

lCl

θθθ

，

{1,2,,}

∈

(1)

with

,||||

CCCC

θθ

=Ψ=

and

ˆ ˆ

ˆ,||||

llll

θθ

=Ψ=

()

< (2)

where kc is a common sparse parameter of θc and kl is an

innovation sparse parameter of θl.

Thus, the signal xc is common to all of

({1,2,,})

xlJ

∈

and has sparse coefficient vector θc in

basis ψ, and the signal ˆ

({1,2,,})

xlJ

∈

is the unique

portions of xl and has sparse coefficient vector

in the

same basis. Denote that Ωc is a tight support set of the

nonzero values in θc and Ωl is a tight support set of the

nonzero values in

To make linear measurements, denote the measure-

ment matrix

()

lijnm

Φ=

({1,2,,})

∈

for the mul-

tisignal ensembles, where a second basis matrix Φl is inco-

herent with Ψ. Thus, a small number of noiseless measure-

ments

((1),

llll

yxy=Φ=

,())({1,2,,})

ynlJ

∈

contain sufficient information for approximate reconstru-

ction [1,2]. Mathematically, this can be reduced to a

standard linear algebra problem: we wish to find

T. J. WANG ET AL.

460

({1,2,,})

xlJ

∈

which explains the measurements

lllll

=Φ=ΦΨ

({1,2,,})

∈

2.2. Joint Reconstruction of Multiple Signal

Ensembles via

Optimization

To give ourselves a firm footing for analyses, we firstly

consider single signal reconstruction based on the CS

theory, mainly to exploit intra-signal structure at a single

node. CS encodes a workable approximation of the sin-

gle compressible signal

({1,2,,})

xlJ

∈

with l

sampling resources and signal reconstruction can be

achieved by Basis Pursuit (BP) [1,2] or Orthogonal

Matching Pursuit (OMP) [3]. OMP allows faster recon-

struction at the expense of more measurements.

Formally, BP needs to solve the following

optimi-

zation problem

(P1)

min||||

subject to

lllll

=Φ=ΦΨ

({1,2,,})

∈

(3)

The simulation results in [2] state that there exists meas-

urements n ≥ck (oversampling factor c ≥ 4) are required

to reconstruct

with high probability, using linear

programming methods e.g. interior point method and

simplex method. That is, an optimal reconstructed signal

=Ψ

can be achieved by an optimal sparse solution

of the problem (P1).

In addition to single signal encoding and decoding

methods, the jointly encoding and decoding methods of

multiple signal ensembles are considered in DCS. DCS

expects that 1)

()

ckk

({1,2,,})

∈

measurements

suffice to reconstruct x1, 2)

()

ckk

∑

measurements

suffice to reconstruct multiple signal ensembles x1,..., xJ,

for there exists

∑

nonzero elements in x1,..., xJ

Furthermore, the recovery problem can be formulated

using matrices and vectors as























Φ=





ΨΨ





Ψ=



ΨΨ



%MO(4)

In order to sufficiently utilize inter-signal correlation of

multiple signal ensembles, we assume that

Φ==Φ=Φ

and then

can be rewritten as

(,,)

diag

Φ=ΦΦ

. It is possible to let Sink previously

send the same random seed to all sensor nodes in the

interesting field and then the same pseudorandom matrix

Φ can be generated using simple algorithm with seed at

each node.

With sufficient sampling, DCS can reconstruct multi-

ple signal ensembles by solving the following

opti-

mization problem

(P2)

min||||

subject to y

=ΦΨ

(5)

Due to the optimal spare solution

of the problem

(P2), we can get the corresponding reconstructed multi-

signal ensembles

=Ψ

3. Mobile-Agent-Based Adaptive Data

Fusion Algorithm

The DCS theory proposes a framework for joint recon-

struction of compressible multi-signal ensembles. How-

ever, each single node independently encodes in DCS,

which does not sufficiently utilize the joint sparsity of

multi-signal ensembles. This operation makes each node

have to transmit a lot of measurements. In this session,

we focus on reducing measurements required to transmit

at each node by mobile-agent-based data fusion in WSN.

A WSN under a DCS framework, as shown in Figure

1, consists of three types of components: Sink, sensor

nodes and communication network. With energy restric-

tion, sensor nodes can not directly communicate with

Sink. For example, the encoding results of a node Sl+1 in

the interesting field are transmitted to Sink by multi skips

routing in Figure 1. Other nodes do the same works. In

Figure 1, we model a WSN as a graph G=(V,E), where

−

Figure 1. A WSN under DCS framework. Circles denote

sensor nodes. The communication distance between node

and node 1

({1,,1})

SlJ

∈−

and the communica-

tion distance between Sink and

is approximately as

by the shortest multiple skips routing. For being simple,

other links representing the communication links among

nodes and Sink are omitted. On the other hand, a route

{,,,,,}

SJS

SSSS

represents MA data fusion routing.

T. J. WANG ET AL.

461

{,,,}

VSSS

and E denotes an edge set represent-

ing the communication links between node-pairs or links

between Sink and nodes. In many applications, a distant

Sink

retrieves relevant interesting field information

from the sensor nodes. Let

({1,,})

dlL

∈

be the total

communication distance between Sink and a node

({1,,})

SlL

∈

by the shortest multiple skips routing.

For being simple, Sink is assumed to be far away from

the interesting field so that 1

SSLS

ddd

≈≈≈

and

({1,,1})

Sll

ddlL

∈−

, where

denotes the com-

munication distance between node-pairs

and

[13].

We next describe the communication architecture of

WSN in Figure 1 to motivate the formulation of two data

fusion algorithms for multiple signal ensembles. Assume

that a connected subgraph '''

(,)

GVEG

=⊆

is found,

where

contains Sink and encode nodes, i.e.,

{,,,}

VSSSV

=⊂

(,)

IHJL

, and

de-

notes a edge set representing all communication links in

. For a node

({1,,})

SlJ

∈

, its node weight

()

denotes the amount of data outgoing from

. An edge

({1,,1})

eElJ∈∈−

is denoted by

(,)

lll

eSS

The weight of edge

is equivalent to the weight of

i.e.,

()()

wewS

=. Two metrics,

()

and

()

, are

associated with each edge, describing the transmission

cost and fusion cost on the edge, respectively. In many

WSN applications, however, the fusion cost may be neg-

ligible. For being simple, we do not consider fusion cost

in this paper.

The unit cost of the link for transmitting data from S1

is abstracted as ,1

() r

lll

ced

βε

, where β and r are

tunable parameters based on the radio propagation [14].

Thus the transmission cost

()

()()()

lll

tecewe

(6)

Similarly, we approximately define

({1,,})

elJ

∈

the communication links between a node Sl and Sink by

the shortest multiple skips routing, and then the trans-

mission cost is approximately as

()()

SlSl

tece

()({1,,})

welJ

∈

, where

()

and

()

are the

unit transmission cost and the weight of

. Obviously,

we can get

()()

Sll

cece

, for

Sll

From above definitions, the total network energy con-

sumption in

'''

(,)

GVE

= with different computing

models can be calculated. We firstly consider total net-

work energy consumption of DCS. According to encod-

ing method of a single signal, we assume that individual

node

({1,,})

SlJ

∈

can gain a sparse coefficient vec-

tor

({1,,})

θ∈

by projecting a sensing signal

({1,,})

xlJ

∈

into a basis matrix

. This operation

may consume some computational energy, but it does not

affect the total network energy consumption and can be

omitted compared to transmission cost.

To conveniently explain the network energy consump-

tion, we assume that Cl

Ω∩Ω=∅

. Single signal recon-

struction, therefore, needs

measurements with nl=

c(kc+kl) in a CS framework, and then the total network

energy consumption of DCS can be calculated as follows

()()()()

DCSSlSlSCl

Ccewedckk

βε

==++

∑∑ (7)

where the number of measurements

()

lCl

nckk

di-

rectly denotes the weight

()

We consider the network energy consumption of two

mobile-agent-based data fusion algorithms. Generally

speaking, MA is a special kind of software with small

size, whose transmission cost can be omitted compared

to transmission cost of larger amount of sensing informa-

tion. We will not consider MA transmission cost. Sink

predetermined the MA routing 1

{,,,,,}

SJS

SSSS

by GCF. The detailed mobile-agent-based data fusion

process is presented as follows.

In initialize stage, MA migrates toS1and obtains meas-

urements y1 with

110

||||

=. Subsequently, it migrates

to S2 and finds θc

and

by contrasting sparse coef-

ficients θ1 and θ2. Thus, it can calculate the common

measurements yc corresponding to the common sparse

component θ1 of the signal ensembles. This means that

measurements y1 and y2 can be divided into

yyy

and

yyy

, where

and

correspond to the

sparse innovation component

and

. MA carrying

measurements

and

with 2

()(

weck

)

+ migrates to

. We then repeat above process

on remaining nodes along MA routing until MA returns

to Sink. Such process is a typical mobile-agent-based

data fusion process. In this paper, we term this process a

mobile-agent-based Full Data Fusion (FDF) algorithm

compared to the following adaptive data fusion process.

The total network energy consumption of FDF is shown

as follows

,11

()()()()

()()

FDFllSJSJ

llCl

SCJ

Ccewecewe

dckkk

βε

−

=++++

+++++

∑

∑L

(8)

We interest in comparing the total energy consumption

T. J. WANG ET AL.

462

of DCS and FDF. The total transmission cost can be cal-

culated as follows 1

()(1)()

DCSFDFSClll

CCdJckdck

βεβε

−

−=+−−+

∑

(()())

Jrr

SClll

dckdck

βεβε

−

=+−+

∑ (9)

Note that

Sll

and

, it is easy to get

DCSFDF

CC> (10)

As expected, the inequality (10) means that the total

transmission cost of DCS is much larger than FDF. By

analyzing FDF in detail, we find another challenge that

MA will carry more and more amount of data fusion

results along the MA routing. However, data fusion at a

node

({2,,})

∈

only needs the common meas-

urements

. If MA still carries all front innovation

measurements

−

, it is not in favor of saving

communication cost. This result brings a question

whether we can avoid transmitting an amount of the in-

novation measurements. In this regard, we establish the

following data fusion algorithm named mobile-agent-

based Adaptive Data Fusion (ADF) algorithm. Different

from in FDF, MA only carries the common measure-

ments

in ADF. Concretely, MA can calculate

({2,,})

∈

by contrasting

and

({2,,

l∈

})

, when it carrying

migrates to

({2,,})

∈

. This allows

({2,,})

∈

to be

divided into

lCl

yyy

in which the number of the

innovation measurement

is ˆ

nck

=. MA carrying

measurements

with ()

weck

= continuously mi-

grates to

. On the other hand, measurements

are

directly transmitted to Sink. We then repeat above proc-

ess on remaining nodes along the same MA routing as

FDF until MA returns to Sink. Then, the total network

energy consumption of ADF is expressed as follows

121

()()

(()())()()

ADFC

rrr

llCSlSCJ

Cdckk

dckdckdckk

βε

βεβεβε

−

=++

+++++++

∑(11)

We also attend to compare the total energy consumption

of FDF and ADF as follows

()0

FDFADFlll

CCdckβε

−

−=+>

∑ (12)

i.e.,

FDFADF

CC> (13)

From (10) and (13), it can be shown that

DCSFDFADF

CCC>> (14)

From (14), we can easily obtain the benefits of ADF.

Firstly, based on DCS, ADF also sufficiently utilizes

both temporal (intra-signal) and spatial (inter-signal)

correlations of multi-signal ensembles to analyze single

signal sparsity structure and multi-signal ensembles

jointly sparsity structure. These sparsity structures make

it possible to perform data fusion of multi-signal ensem-

bles. Second, the innovation measurements are allowed

to directly transmit to Sink, while MA only carries the

common measurements. It benefits reducing transmis-

sion cost. So we can say that ADF provides the optimal

strategy for minimizing total transmission measurements

and transmission cost compared to DCS and FDF.

According to the above discussion, we can reconstruct

multi-signal ensembles by solving the following

op-

timization problem

(P3)

min||||

subject to

=ΦΨ

(15)

where







, 1







, 1





Φ=





MLOM





Ψ=





MOM

We can obtain ****

(,,,)

xxxx

with an optimal

sparse solution ****

(,,,)

θθθθ

, where

=Ψ

and **

,({1,,})

xlJ

θ=Ψ∈

. Furthermore, multi-signal

ensembles can be reconstructed by

***

lCl

xxx

({1,,})

∈

The above results focus on theoretical analyses of sav-

ing transmission cost in ADF. On the other hand, we are

interested in comparing the joint reconstruction per-

formance of DCS, FDF and ADF. The following simula-

tion results are presented illustrating the better joint re-

construction performance of ADF.

4. Simulation

In our setup, sensor nodes are randomly distributed in a

region of a

5050

square. The distance between

Sink and the interesting field is

400

=. When con-

sidering transmission cost, we set

100//

pJbitm

β=,

and

100/

nJbit

ε= [12] in (6). Furthermore, we

consider a series of example multiple signal ensembles

that satisfy the conditions of joint sparsity

model. The signal components 1

,,,

xxx

are as-

sumed to be sparse in Discrete Cosine Transform (DCT)

matrix

with sparse parameters 1

,,,

kkk

, re-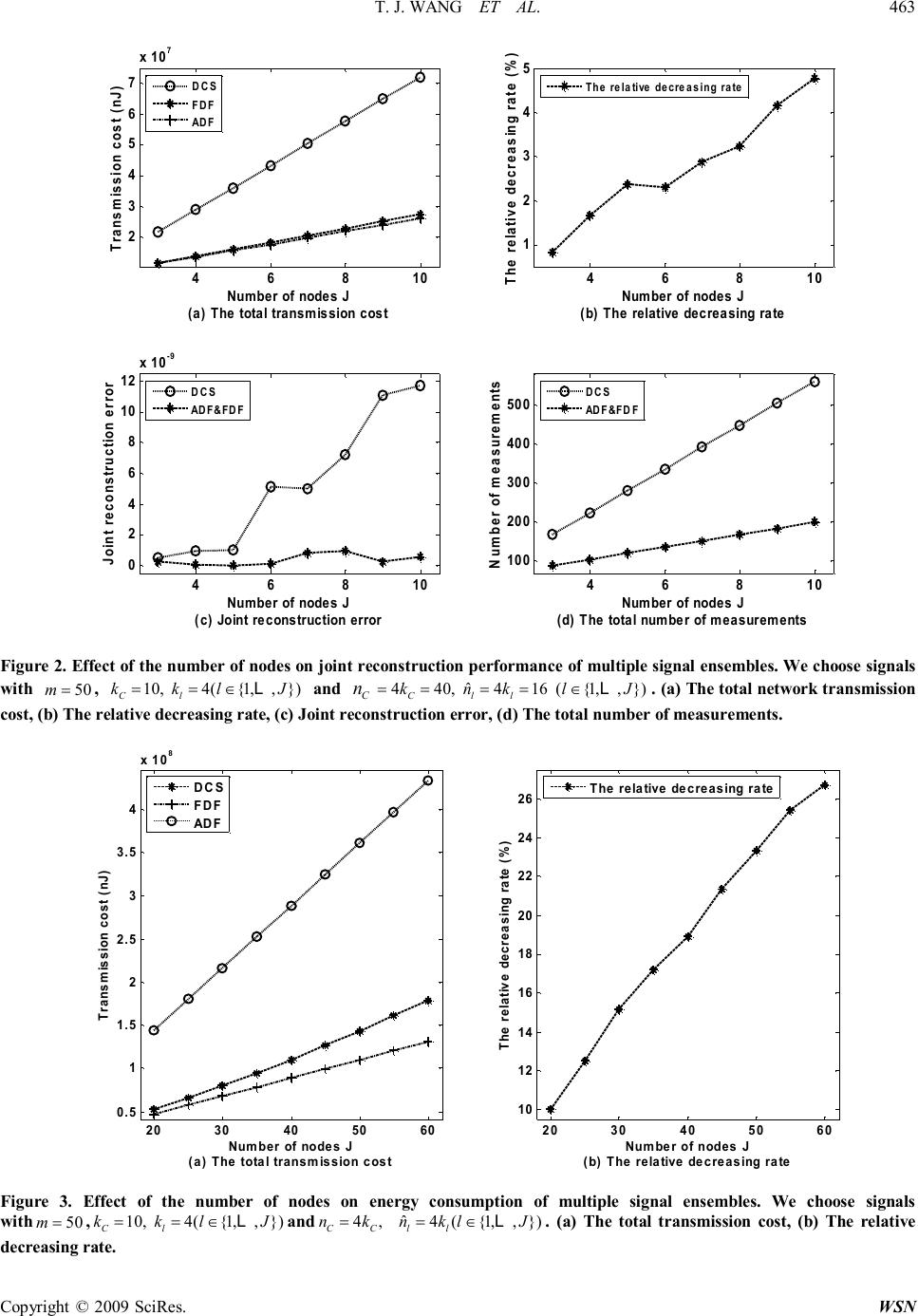

T. J. WANG ET AL.

463

46810

x 10

Number of nodes J

(a) The total transmission cost

Transmission cost (nJ)

468 10

Number of nodes J

(b) The relative decreasing rate

The relative decreasing rate (%)

468 10

12 x 10

-9

Number of nodes J

Joint reconstruction error

468 10

100

200

300

400

500

Number of nodes J

(d) The total number of measurements

Number of measurements

DCS

FDF

ADF

The relative decreasing rate

DCS

ADF&FDF

DCS

ADF&FDF

Figure 2. Effect of the number of nodes on joint reconstruction performance of multiple signal ensembles. We choose signals

with

10,

4({1,,})

klJ

=∈

and

440,

416

({1,,})

∈

. (a) The total network transmission

cost, (b) The relative decreasing rate, (c) Joint reconstruction error, (d) The total number of measurements.

20 3040 50 60

0.5

1.5

2.5

3.5

x 10

Number of nodes J

(a) The total transmission cost

Transmission cost (nJ)

20 3040 50 60

Number of nodes J

(b) The relative decreasing rate

The relative decreasing rate (%)

DCS

FDF

ADF

The relative decreasing rate

Figure 3. Effect of the number of nodes on energy consumption of multiple signal ensembles. We choose signals

with

10,

4({1,,})

klJ

=∈

and

4({1,,})

nklJ

=∈

. (a) The total transmission cost, (b) The relative

decreasing rate.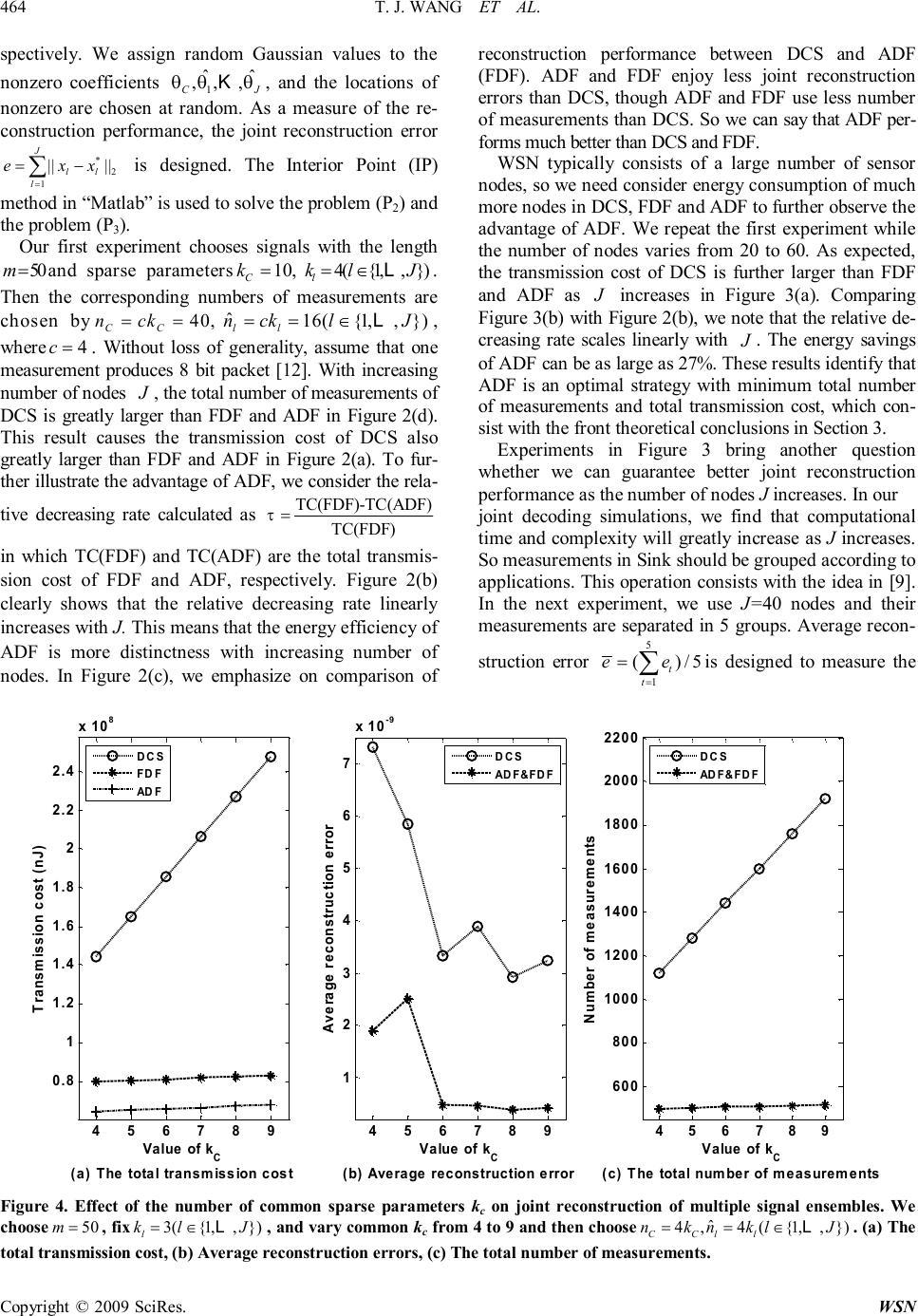

T. J. WANG ET AL.

464

spectively. We assign random Gaussian values to the

nonzero coefficients 1

,,,

θθθ

, and the locations of

nonzero are chosen at random. As a measure of the re-

construction performance, the joint reconstruction error

||||

exx

=−

∑ is designed. The Interior Point (IP)

method in “Matlab” is used to solve the problem (P2) and

the problem (P3).

Our first experiment chooses signals with the length

and sparse parameters

10,

4({1,,})

klJ

=∈

Then the corresponding numbers of measurements are

chosen by

40,

nck==ˆ

16({1,,})

ncklJ

==∈

where

. Without loss of generality, assume that one

measurement produces 8 bit packet [12]. With increasing

number of nodes

, the total number of measurements of

DCS is greatly larger than FDF and ADF in Figure 2(d).

This result causes the transmission cost of DCS also

greatly larger than FDF and ADF in Figure 2(a). To fur-

ther illustrate the advantage of ADF, we consider the rela-

tive decreasing rate calculated as

TC(FDF)-TC(ADF)

TC(FDF)

τ=

in which TC(FDF) and TC(ADF) are the total transmis-

sion cost of FDF and ADF, respectively. Figure 2(b)

clearly shows that the relative decreasing rate linearly

increases with J. This means that the energy efficiency of

ADF is more distinctness with increasing number of

nodes. In Figure 2(c), we emphasize on comparison of

reconstruction performance between DCS and ADF

(FDF). ADF and FDF enjoy less joint reconstruction

errors than DCS, though ADF and FDF use less number

of measurements than DCS. So we can say that ADF per-

forms much better than DCS and FDF.

WSN typically consists of a large number of sensor

nodes, so we need consider energy consumption of much

more nodes in DCS, FDF and ADF to further observe the

advantage of ADF. We repeat the first experiment while

the number of nodes varies from 20 to 60. As expected,

the transmission cost of DCS is further larger than FDF

and ADF as

increases in Figure 3(a). Comparing

Figure 3(b) with Figure 2(b), we note that the relative de-

creasing rate scales linearly with

. The energy savings

of ADF can be as large as 27%. These results identify that

ADF is an optimal strategy with minimum total number

of measurements and total transmission cost, which con-

sist with the front theoretical conclusions in Section 3.

Experiments in Figure 3 bring another question

whether we can guarantee better joint reconstruction

performance as the number of nodes J increases. In our

joint decoding simulations, we find that computational

time and complexity will greatly increase as J increases.

So measurements in Sink should be grouped according to

applications. This operation consists with the idea in [9].

In the next experiment, we use J=40 nodes and their

measurements are separated in 5 groups. Average recon-

struction error 5

()/5

∑

is designed to measure the

456789

0.8

1.2

1.4

1.6

1.8

2.2

2.4

x 10

Value of k

(a) The total transmission cost

Transmission cost (nJ)

DCS

FDF

ADF

456789

x 10

-9

Value of k

(b) Average reconstruction error

Average reconstruction error

DCS

ADF&FDF

4 567 8 9

600

800

1000

1200

1400

1600

1800

2000

2200

Value of k

Number of measurements

DCS

ADF&FDF

Figure 4. Effect of the number of common sparse parameters kc on joint reconstruction of multiple signal ensembles. We

choose

, fix

3({1,,})

klJ

=∈

, and vary common kc from 4 to 9 and then choose ˆ

4,4({1,,})

CCll

nknklJ

==∈

. (a) The

total transmission cost, (b) Average reconstruction errors, (c) The total number of measurements.

T. J. WANG ET AL.

465

2 4 6

0.5

1.5

2.5

3.5 x 10

Value of k

(a) The total transmission cost

Transmission cost (nJ)

24 6

0.5

1.5

2.5

3.5

x 10

-7

Value of k

(b) Average reconstruction error

Average reconstruction error

246

500

1000

1500

2000

2500

Value of k

Number of measurements

DCS

FDF

ADF

DCS

ADF&FDF

DCS

ADF&FDF

Figure 5. Effect of the number of innovation sparse parameters

on joint reconstruction of multiple signal ensembles. We

choose

, fix

and vary

({1,,})

klJ

∈

from 1 to 7, and then choose

4({1,,})

nklJ

=∈

. (a) The total

transmission cost, (b) Average reconstruction errors, (c) The total number of measurements.

reconstruction performance, where

(1,,5)

et=

is the

joint reconstruction error of every group. We perform

experiments with the length of signals

and in-

novation sparse parameters

({1,,})

∈

, while

the common sparse parameter kc varies from 4 to 9. The

obtained results in Figure 4 (a)-(c) show the similar con-

clusions in Figure 2 and Figure 3. The number of com-

mon sparse parameters kc greatly affects the total trans-

mission cost of DCS while not FDF and ADF, for DCS

need each node to transmit the common measurements

while FDF and ADF avoid this operation by data fusion.

This sufficiently reveals the advantage of mobile-agent-

based data fusion algorithms. Moreover, the average re-

construction error of DCS, FDF and ADF decrease bene-

fiting from the increasing number of measurements. This

means joint reconstruction performance can be improved

by increasing the total number of mea- surements.

The finally experiments focus on effect of the number

of innovation sparse parameters kl on joint reconstruction

of multiple signal ensembles. We repeat the front ex-

periments with the length of signals m=50 and the com-

mon sparse parameter kc=8, while the innovation sparse

parameter kl (l∈{1,…J}) varies from 1 to 7. As kl (l∈

{1,…J}) increasing, the total transmission cost and the

number of measurements of FDF and ADF fleetly in-

crease compared to Figure 4. Figure 5(a) and Figure 5(c)

reveal that the performance of data fusion is influenced

by the innovation sparse parameters kl, for kl represent

the differences among multi-signal ensembles. At the

expense of more measurements and energy cost, we can

obtain multi-signal ensembles with more details. At the

same time, we gain the better joint reconstruction per-

formance in Figure 5(b), for the total number of meas-

urements increases.

As can be seen, above experiments imply that ADF

sufficiently takes advantage of intra- and inter-signal

correlation of multi-signal ensembles by mobile-agent-

based data fusion. So ADF enjoys better performances

than DCS and FDF.

5. Conclusions

Distributed Compressed Sensing (DCS) extends the the-

ory and practice of Compressed Sensing (CS) to multi-

signal ensembles. A joint sparsity model for multi-signal

ensembles with both intra- and inter-signal correlation

captures the essence of real physical scenarios. This pa-

per provides a new mobile-agent-based Adaptive Data

Fusion (ADF) algorithm. ADF can greatly reduce the

total number of measurements for successful joint recon-

struction compared with DCS. Moreover, ADF can

greatly reduce transmission cost and network load. Ex-

tensive experiments demonstrate that it indeed leads to

T. J. WANG ET AL.

466

better performance than DCS and mobile-agent-based

Full Data Fusion (FDF).

6. References

[1] D. Donoho, “Compressed sensing,” IEEE Trans. on In-

formation Theory, Vol. 52, No. 4, pp. 1289–1306, April

2006.

[2] Y. Tsaig and D. Donoho, “Extensions of compressed

sensing,” Signal Processing, Vol. 86, No. 3, pp. 533–548,

March 2006.

[3] J. Tropp and A. Gilbert, “Signal recovery from random

measurements via orthogonal matching pursuit,” IEEE

Transactions on Information Theory, Vol. 53, No. 12, pp.

4655–4666, December 2007.

[4] Y. C. Kim, S. S. Narayanan, and K. S. Nayak, “Acceler-

ated three-dimensional upper airway MRI using com-

pressed sensing,” Magnetic Resonance in Medicine, Vol.

61, pp. 1434–1440, 2009.

[5] M. Mishali and Y. C. Eldar, “Blind multi-band signal

reconstruction: compressed sensing for analog signals,”

IEEE Transactions on Signal Processing, Vol. 57, No. 30,

pp. 993–1009, March 2009.

[6] M. F. Duarte, S. Sarvotham, D. Baron, and M. B. Wakin,

“Distributed compressed sensing of jointly sparse sig-

nals,” in 39th Asilomar Conference on Signals, Systems

and Computers, pp. 1537–1541, 2005.

[7] S. Pradhan and K. Ramchandran, “Distributed source

coding using syndromes (DISCUS): Design and con-

struction,” IEEE Trans. on Information Theory, Vol. 49,

pp. 626–643, 2003.

[8] Z. Xiong, A. Liveris, and S. Cheng, “Distributed source

coding for sensor networks,” IEEE Signal Processing

Magazine, Vol. 21, pp. 80–94, September 2004.

[9] D. Baron, M. B. Wakin, M. F. Duarte, S. Sarvotham, and

R. G. Baraniuk, “Distributed compressed sensing,” http://

www.dsp.ece.rice.edu/cs.

[10] J. Meng, H. Li, and Z. Han, “Sparse event detection in

wireless sensor networks using compressive sensing,”

The 43rd Annual Conference on Information Sciences

and Systems (CISS’09), Baltimore, MD, 2009.

[11] A. H. Phan, A. Cichocki, and K. S. Nguyen, “Simple and

efficient algorithm for distributed compressed sensing,”

IEEE Machine Learning for Signal Processing (MLSP’

08), pp. 61–66, October 2008.

[12] Q. Wu, N. S. V Rao, J. Barhen, S. S. Iyengar, V. K.

Vaishnavi, H. Qi, and K. Chakrabarty, “On computing

mobile agent routes for data fusion in distributed sensor

networks, ” IEEE Transactions on Knowledge and Data

Engineering, Vol. 16, No. 6, pp. 740–753, June 2004.

[13] W. Bajwa, J. Haupt, and A. Sayeed, “Compressive wire-

less sensing,” IPSN’06, Nashville, Tennessee, USA, pp.

19–21, 2006.

[14] H. Luo, J. Luo, Y. Liu, and S. K. Das, “Adaptive data

fusion for energy efficient routing in wireless sensor

networks,” IEEE Transactions on Computers, Vol. 55, No.

10, pp. 1286–1299, October 2006.