Paper Menu >>
Journal Menu >>
 Wireless Sensor Network, 2009, 1, 453-457 doi:10.4236/wsn.2009.15054 Published Online December 2009 (http://www.scirp.org/journal/wsn). Copyright © 2009 SciRes. WSN 453 Research on Blind Source Separation for Machine Vibrations Weiguo HUANG, Shuyou WU, Fangrang KONG, Qiang WU Department of Precision Machinery and Precision Instrumentation, University of Science and Technology of China, Hefei, China Email: wghuang@mail.ustc.edu.cn Received August 3, 2009; revised August 18, 2009; accepted August 20, 2009 Abstract Blind source separation is a signal processing method based on independent component analysis, its aim is to separate the source signals from a set of observations (output of sensors) by assuming the source signals in- dependently. This paper reviews the general concept of BSS firstly; especially the theory for convolutive mixtures, the model of convolutive mixture and two deconvolution structures, then adopts a BSS algorithm for convolutive mixtures based on residual cross-talking error threshold control criteria, the simulation test- ing points out good performance for simulated mixtures. Keywords: Blind Source Separation, Independent Component Analysis, Convolutive Mixtures, Machine Vibration, Residual Cross-Talking Error 1. Introduction Blind source separation (BSS) is a typical tool to recover source signals from several observations usually pro- vided by a set of sensors. Due to the lack of prior knowledge of the source signals, generally, this method considers an assumption of independence between the sources. It has been successfully used in many fields, such as biomedicine, telecommunications, speech proc- essing, underwater acoustics [1–3]. But BSS methods have seldom been used for monitoring or diagnosing the mechanical devices, in many cases the signals obtained by sensors consist of some useless signals, such as envi- ronment noise, other mechanical devices [4–6]. In these condition, using BSS as a preliminary step will reduce, even remove the useless signals, which can significantly improve the efficiency and accuracy of the condition monitor and fault diagnosis. At present, most of BSS works are related to the sepa- ration of linear mixtures of sources. However, the vibra- tion of mechanical devices is complex, and so is the propagation medium. The mechanical vibration signals are often convolutive mixtures [7]. Consequently, this paper mainly describes BSS for convolutive mixtures and its application to mechanical vibrations. 2. BSS 2.1. BSS Introduction Blind source separation is a signal processing technique by which unobserved signals, also called sources, are recovered from the observation of several mixtures. The term “Blind” includes two facts: both the source signals and the mixing structure are unknown. In the present research work, most are assuming the mutual independ- ence of the sources. This is the fundamental basis of BSS. For condition monitoring and fault diagnosis, the ob- served signals are usually the output of a set of sensors and linear combinations of the sources. Just as Figure 1 shows. Figure 1. Observed signals and sources.  W. G. HUANG ET AL. 454 In Figure 1, the S1, S2, S3,…Sq denote the sources and the x1, x2, x3,…xp denote the observations (output of sensors). When condition monitoring and fault diagnosing of me- chanical devices, the P observations (output of P sensors) are the linear combinations of the q sources. In this way, the i-th observation (output of the i-th sensors) is: 1 () () q iijji j x astn t (1) 1,2, 3,,ip where aij is the linear combination coefficients, ni(t) denotes the environment noise received by the i-th sen- sor. The noise may be considered as a source signal, in this way, the mathematical model of BSS could be shown as () () X tASt (2) where 12 ()[ (),(),,()] T p X txtxt xt 12 ()[ (),(),,()] T q Sts tstst denotes the p observed signals, which are the available data. A is the unknown p ×q mixing matrix, which denotes the unknown propa- gation. denotes the q source sig- nals, which include the noises. Here, generally, p ≥ q and denotes the transpose operator. []T Here, assuming the mixing matrix A is invertible and the sources Si(t) (i=1,2,…q) are statistically independent. The assumption of independence between the sources is physically plausible because they have different origins [8]. The kernel of BSS is to find a q *p separation matrix B and the recovered signals are ()()() ()St BXt BAStCSt (3) If matrix B could make the matrix C be an identity matrix, it could be concluded that the source signals have been separated perfectly. The general model of BSS could be shown as Figure 2. 2.2. Model of Convolutive Mixture [9] For condition monitoring and fault diagnosis, vibration analysis involves a convolutive mixture because of the propagation medium (structure of the system). The envi- ronment noise may be considered as a source signal. The general model of a convolutive mixture can be repre- sented as in the Figure 3 for two source signals and two observation signals (p=q=2) to be simplified. Moreover, if the sensors are located near the source signals, respectively, we could consider that the filters Figure 2. BSS general model. Figure 3. Two source signals and two observation signals model. A11 and A22 are equal to 1. In fact, it is significantly for condition monitoring and fault diagnosis that the sensors are as close as possible to the origins. In this way, we can get a simplified model: 11 122 22112 ()()* () ()* ()() x nsnAsn x nAsnsn (4) Using the Z transform 11122 22112 ()()() () ()() ()() XzSzA zSz XzAzSzSz (5) and the matrix formulation ()()() X zAzSz (6) where 12 21 1 () 1 A Az A (7) assuming that the filters of A(z) can be modeled by Lth-order causal transverse filters, so that the matrix are given by ()Az 1 0 () () L k ij ij k A zakz (8) Formulation (5) may be expanded in the time domain 1 11 122 0 1 22112 0 ()()() () ()() ()() L k L k x nsn aksnk x naksnks n (9) 2.3. Separation Principle and Criteria Theoretically, if the mixing matrix A is invertible, and the separation matrix B is the inverse matrix of the mix- ing matrix A, it could be reconstituted the source signals perfectly. But, in fact, the mixing matrix A is unknown; we could not obtain the separation matrix B by A di- rectly. In the case of the Figure 3, Herault [2] proposed a solution Copyright © 2009 SciRes. WSN  W. G. HUANG ET AL.455 Figure 4. Recursive structure for the BSS. Figure 5. Direct structure for the BSS. based on a recursive architecture, which can be general- ized in the case of convolutive mixtures modeled by FIR filters as Figure 4: Recursive structure. Also, it can be modeled by Figure 5: Direct structure. In the Z-domain, the relationship between recovered signals and observation signals is ~ 11 12 ~ 21 2 12 21 2 () 1() () 1 () () 1 1()() () Xz Bz Sz Bz Xz BzBz Sz (10) Therefore, the relationship between source signals and recovered signals is 112 2112121 212121 122 12 21 2 1()() ()()() () 1 ()() 1()()() 1()() () BzAzAz BzSz Sz A zBzBzAzSz BzBz Sz (11) For the Formulation (10), If 1212 () () B zAz and 21 21 () () B zAz, Then ()(), {1,2} ii Sz Szi (12) If 12 21 1 () () Bz Az and 21 12 1 () () Bz A z , then ()() (),{1,2} iij j SzAzSzi j (13) In the case of the Formulation (13), the filters Bij(z) are infinite impulse response, so only the case of the Formu- lation (12) is valid. In practice, the mixing filters Aij(z) are unknown, therefore, we must estimate them by a method, which could be a stochastic iteration by maxi- mizing the independence. (1, )(, )[(()) (())],{1,2},[0,] ijijn ij bnkbnkuEfsngsn kijkL (14) where bij (n,k) is the k-th coefficient of filter Bij at the n-th iteration, un is a positive adaptation gain, () f and () g are non-linear functions, such as3 () f xx and () g xx . 2.4. Performance Criteria The separation performances two aspects: Residual cross-talking error (RCTE), defined as 2 2 () (,) 10lg() ii ii i Es s RCTE ssEs (15) This could verify the quality of recovered signals, gen- erally, when its value is less than –20db, we can consider that the recovered signals are correct. For the computing speed, this paper adopts the rule based on RCTE threshold control criteria [10] Figure 6. Source signals. Figure 7. Observed signals. Copyright © 2009 SciRes. WSN 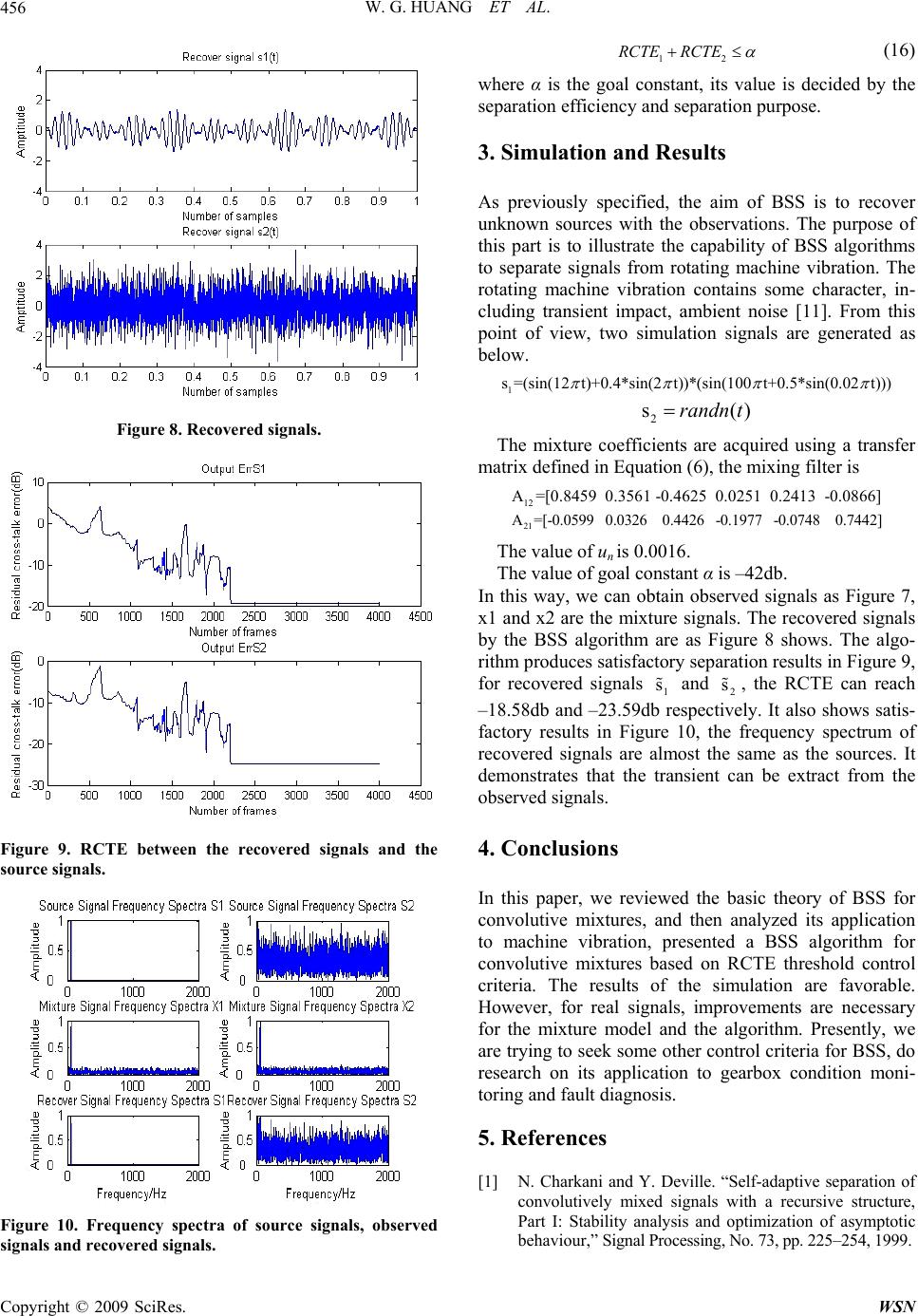 W. G. HUANG ET AL. 456 Figure 8. Recovered signals. Figure 9. RCTE between the recovered signals and the source signals. Figure 10. Frequency spectra of source signals, observed signals and recovered signals. 12 RCTE RCTE (16) where α is the goal constant, its value is decided by the separation efficiency and separation purpose. 3. Simulation and Results As previously specified, the aim of BSS is to recover unknown sources with the observations. The purpose of this part is to illustrate the capability of BSS algorithms to separate signals from rotating machine vibration. The rotating machine vibration contains some character, in- cluding transient impact, ambient noise [11]. From this point of view, two simulation signals are generated as below. 1 s=(sin(12 t)+0.4*sin(2 t))*(sin(100 t+0.5*sin(0.02 t))) 2 s()randn t The mixture coefficients are acquired using a transfer matrix defined in Equation (6), the mixing filter is 12 A=[0.8459 0.3561 -0.4625 0.0251 0.2413 -0.0866] 21 A=[-0.0599 0.0326 0.4426 -0.1977 -0.0748 0.7442] The value of un is 0.0016. The value of goal constant α is –42db. In this way, we can obtain observed signals as Figure 7, x1 and x2 are the mixture signals. The recovered signals by the BSS algorithm are as Figure 8 shows. The algo- rithm produces satisfactory separation results in Figure 9, for recovered signals and , the RCTE can reach –18.58db and –23.59db respectively. It also shows satis- factory results in Figure 10, the frequency spectrum of recovered signals are almost the same as the sources. It demonstrates that the transient can be extract from the observed signals. 1 s 2 s 4. Conclusions In this paper, we reviewed the basic theory of BSS for convolutive mixtures, and then analyzed its application to machine vibration, presented a BSS algorithm for convolutive mixtures based on RCTE threshold control criteria. The results of the simulation are favorable. However, for real signals, improvements are necessary for the mixture model and the algorithm. Presently, we are trying to seek some other control criteria for BSS, do research on its application to gearbox condition moni- toring and fault diagnosis. 5. References [1] N. Charkani and Y. Deville. “Self-adaptive separation of convolutively mixed signals with a recursive structure, Part I: Stability analysis and optimization of asymptotic behaviour,” Signal Processing, No. 73, pp. 225–254, 1999. Copyright © 2009 SciRes. WSN  W. G. HUANG ET AL. Copyright © 2009 SciRes. WSN 457 [2] C. Jutten and J. Herault, “Blind separation of sources, Part 1: An adaptive algorithm based on neuromimetic structure,” Signal Processing, No. 24, pp. 1–10, 1991. [3] M. Gaeta, F. Briolle, and P. Esparcieux, “Blind separa- tion of sources applied to convolutive mixtures in shallow water,” IEEE Signal Process, Workshop Higher Order Statistics Banff, Canada, pp. 340–343, July 1997. [4] N. Bouguerriou, M. Haritopoulos, C. Capdessus, and L. Allam, “Novel cycostationarity based blind source sepa- ration algorithm using second order statistical properties: Theory and application to the bearing defect diagnosis,” Mechanical Systems and Signal Processing, No. 19, pp. 1260–1281, 2005. [5] G. Gelle, M. Colas, and G. Delaunay, “Blind sources separation applied to rotating machines monitoring by acoustical and vibrations analysis,” Mechanical Systems and Signal Processing, Vol. 14, No. 3, pp. 427–442, 2000. [6] G. Gelle and M. Colas, “Blind sources separation: A tool for rotating machine monitoring by vibrations analysis,” Journal of Sound and Vibration, Vol. 248, No. 5, pp. 865– 885, 2001. [7] J. Antoni, “Blind separation of vibration components: Principles and demonstrations,” Mechanical Systems and Signal Processing, No. 19, pp. 1166–1180, 2005. [8] Y. J. Shen and S. P. Yang, “A new Blind-Source-Separa- tion method and its application to fault diagnosis of rolling bearing,” International Journal of Nonlinear Sciences and Numerical Simulation, Vol. 7, No. 3, pp. 245–250, 2006. [9] H. L. Nguyen Thi and C. Jutten, “Blind source separation for convolutive mixtures,” Signal Processing, No. 45, pp. 209–229, 1995. [10] W. Huang, S. Wu, F. Kong, Q. Wu, and P. Li, “Blind source separation for convolutive mixtures and its appli- cation to machine vibrations,” International Conference on Measuring Technology and Mechatronics Automation, Vol. 1, pp. 598–601, 2009. [11] Q. He, Z. Feng, and F. Kong, “Detection of signal tran- sients using independent component analysis and its appli- cation in gearbox condition monitoring,” Mechanical Sys- tems and Signal Processing, No. 21, pp. 2056–2071, 2007. |

