Control strategy optimization using dynamic programming method for synergic electric system on hybrid electric vehicle

doi:10.4236/ns.2009.13030

Paper Menu >>

Journal Menu >>

Vol.1, No.3, 222-228 (2009)

doi:10.4236/ns.2009.13030

SciRes

Natural Science

Control strategy optimization using dynamic

programming method for synergic electric system on

hybrid electric vehicle

Yuan-Bin Yu, Qing-Nian Wang, Hai-Tao Min, Peng-Yu Wang, Chun-Guang Hao

The State Key Laboratory of Automobile Dynamic Simulation, JiLin University, Changchun, China

Received 23 August 2009; revised 27 September 2009; accepted 22 October 2009.

ABSTRACT

Dynamic Programming (DP) algorithm is used

to find the optimal trajectories under Beijing

cycle for the power management of synergic

electric system (SES) which is composed of

battery and super capacitor. Feasible rules are

derived from analyzing the optimal trajectories,

and it has the highest contribution to Hybrid

Electric Vehicle (HEV). The methods of how to

get the best performance is also educed. Using

the new Rule-based power management strat-

egy adopted from the optimal results, it is easy

to demonstrate the effectiveness of the new

strategy in further improvement of the fuel

economy by the synergic hybrid system.

Keywords: Dynamic Programming; Control

Strategy; Optimization; Synergic Electric System;

HEV

1. INTRODUCTION

Hybrid Electric Vehicle (HEV) could improve fuel

economy and exhaust emission using the electric system

to adjust the load of engine and could make it work in

high efficiency. But this depends on the performance of

the electric system on board. Because of the low power

density of battery, it’s hard to be competent for this pur-

pose. When it was combined with super capacitor to

form a new electric system which was called the Syner-

gic Electric System (SES), could exert both merits,

which is energy and power density [1,2].

Rule-based or fuzzy logic control strategy was used to

supervise the power flow between the two parts at pre-

sent [3,4]. For every state of the SES, each control will

come to a new state，at the same time, we can get a loss

of energy. With regard to a given cycle of motor power

requirement, how to get the best control rate has been

put to us which can achieve the optimal performance of

the system. Dynamic Programming is a numerical

methodology developed for solving sequential or multi-

stage decision problems just like the SES. The algorithm

searches for optimal decisions at discrete points in a time

sequence. It has been shown to be a powerful tool for

optimal control in various application areas [4,5,6,7].

The dissertation proposed the dynamic programming

algorithm from optimum control theory which solve the

problem of overall control rate for SES in the whole

cycle and try to answer the question like what can SES

do on energy-saving.

2. BRIEF INTRODUCTION OF SES

CONFIGURATION AND RULE-BASED

CONTROL ALGORITHM

A hybrid city bus was chosen as a researching flat, and

the SES was made up of 280 Nickel-Hydrogen batteries

units (1.2V\15Ah each) and 120 super capacitors (2.5V

\2000F each). A Buck/ Boost DC/DC power converter

whose Peak / rated power were 60/30kw was used in this

system to coordinate the voltage of battery and capacitor,

and to control the current of capacitor actively. Figure 1

was the layout of SES in this research.

Control objective of SES was as follow: ensure the vehi-

cle’s dynamic as the premise and give full play to the

super capacitor’s “push and pull” role; decrease large

current’s impact; extent battery’s service life; regenerate

braking energy as much as possible to improve fuel

Figure 1. Topology of Buck/Boost DC/DC Converter.

Y. B. Yu et al. / Natural Science 1 (2009) 222-228

223

economy. The principle of the rule-based control strat-

egy is: During the operation, battery provides the aver-

age power requirement; capacitor will give a comple-

ment. The control rule was as follow:

1) if Pm<0, and super capacity was not over charged,

then Pbat=0；

2) or if Pm <Pbat_max, and super capacity was not over

discharged, then Pbat=Pfilter、Pscap=Pm-Pfilter；

3) otherwise Pbat=Pm；

4) when super capacity run out of energy, charge the

capacitor from battery, Pbat =Pchg+Pbat.

The variables’ meanings above are: Pm——the power

required from motor, Pbat ——batteries’ power needed

from motor, Pscap ——capacitor’s power requirement,

Pfilter——filtering power, which is calculated by For-

mula (1).

filter LP

PPHPe







 





load

Pe e













(1)

In the formula: Pload——road resistance; HLP——filter

function; τ、τ’——engine and battery’s low-pass filter

time constant; t——acceleration time; Pm——motor

power required; Pchg——charge power from battery

when capacitor’s state of charge (CSOC) is low. It is the

function of battery’s state of charge (SOC) and is equal

to Pbat_max*（SOC-SOCmin）/ (SOCmax-SOCmin).

The capacitor’s electrical-quantity shortage is deter-

mined by the demand. When the actual voltage of ca-

pacitor is lower than the ideal voltage, it is calculated out

according to vehicle speed as Formula (2). The disserta-

tion provides that the ideal voltage limit is in a reverse

proportion with vehicle speed. The object of setting this

value is to develop a goal of electrical-quantity for ca-

pacitor, which could ensure that it could preserve

enough energy for acceleration when vehicle speed is in

the formula: Vscap——capacitor’s actual voltage of low

and regenerate enough braking energy capacity. When

vehicle speed is high. The speed requirement of the ve-

hicle, the current of single battery, current of SES’s bat-

tery and capacitor according to rule-based control strat-

egy are shown in Figure 2.

max max

scap car









(2)

In the formula: capacitor; max

cap

V——capacitor’s

maximum voltage; vcar——actual vehicle speed;

max

car

——maximum vehicle speed; k——capacitor’s energy

utilization rate in cycle, in value equivalent to 0.75；

Figure 2. Simulation results under Beijing cycle.

3. BRIEF INTRODUCTION OF DYNAMIC

PROGRAMMING CONTROL

ALGORITHM

Dynamic programming is a kind of math method solving

the optimal problem in process of multi-stage decision.

It is proposed and established in the Fifties of 20th Cen-

tury by American mathematicians (Bellman) who claim

the famous Optimum Theory and transmit the process of

multi-decision into a serious of single-stage issue. Multi-

stage problem is a kind of activities which could be di-

vided into several interrelated stages. Each stage needs a

decision. The decision not only decides the benefit of

this stage but also the initial state of next stage. A se-

quence of decisions would be created after every stage’s

decision has been made. The multi-stage decision prob-

lem is to get a control strategy that can optimize the sum

of every stage’s benefit [3]. Dynamic programming al-

gorithm can fully utilize the limited resources which is

an important content of investment-determination. As

for multi-stage determination problem, dynamic pro-

gramming method could be used to make sure the sum

of benefit from every stage optimal [4].

4. DESCRIPTION OF PROBLEM OF

OPTIMIZATION CONTROL

ALGORITHM

The power requirement of motor at every moment is

fulfilled by battery and ultra capacitor. However, be-

cause of the difference between the resistance and the

efficiency of charge and discharge, every decision made

by system at every moment will create impact on the

whole control effect. For the power requirement of mo-

tor is consist of the power of battery and ultra capacitor

at any proportion. So relationship of the power of battery

and ultra capacitor is:

Y. B. Yu et al. / Natural Science 1 (2009) 222-228

224

at scap m

P +P=P （3）

Figure 3. Recursive of system’s state and control object.as

shown in Formula (6).

Every moment, the battery and ultra capacitor in the

SES have the corresponding SOC and CSOC which rep-

resent the state X of battery and ultra capacitor. When

the power flow through battery and ultra capacitor, it can

create an incentive to change the state of the two power

source, at the same time can create power loss J. Ac-

cording to the experiment result of component’s charac-

ter, the resistances of battery and ultra capacitor are

functions of SOC and CSOC and different system loss

would be created under different control rate U. Thus,

conclusions can be drawn that system’s power loss J, at

the same time J is the function of state object X and con-

trol rate U. Recursive equation of X and power loss

equation can be expressed by Formula (4).

G+G

= E((1)())E((1)

())

SOC KSOC KCSOC K

CSOC K









bat Scap

maxmax 

(5)

5. OBJECT OF THE OPTIMIZATION

x(k+1)=f(x(k),u(k))

J((),()

x(k),u(k)x(k),(1-u(k))(1-u(k))

Lxk uk

system

loss

bat ScapDC/DC

loss lossloss

=P （）+P()+P

If every control rate in the cycle is given properly, the

sum of power loss at every moment will decrease to the

minimum. Under the same cycle power requirement, it

can be seen as the best cycle power efficiency, the big-

gest regenerate of braking energy and the best perform-

ance of power. Consequently, optimal goal could be set

(4)

Under given driving cycle, the power requirement

from motor can be drawn, then the system’s loss on this

moment was only decided by the two parts’ state X and

the chosen control rate U. From this moment on, differ-

ent power requirement Pm and control rate U will create

different state X and confront with the problem of

choosing a new control rate till the end of the cycle. Be-

cause the initial condition of vehicle simulation has been

decided, the problem of optimum control rate on SES

can be attributed to: Free optimal control issues on cer-

tain initial condition x(0)=x, as shown in Figure 3.



minmin((),())

Lxk ukG













 (6)

6. CONSTRAINTS

In cycle, the charge and discharge power and the energy

of batteries and capacitors must subject to the limitation

of Formulas (7) and (8).

It is considered that the changes of battery’s state will

have a certain influence on the power loss effect. So,

when calculating the value of J, battery and capacitor’s

electrical-quantity state G should be fully considered.

Calculation of G showed in Formula (5).

PP()P

bat min max

()[0,]

min max

bat bat

EEtEt

batbat bat



 T

(7)

curre n t

current

To Workspace3

Table_W e

To Workspace2

Table_F C

To Workspace1

Table_SO C

Terminator

Power control

model of SES

Power

Bus

Input u1

u1_Theta_c

Buck /Boost

DC/DC

Rint model

of super capacitor

Scap

Rint model of

battery

B atte ry

Add

Figure 4. Solving model of synergic system.

Openly accessible at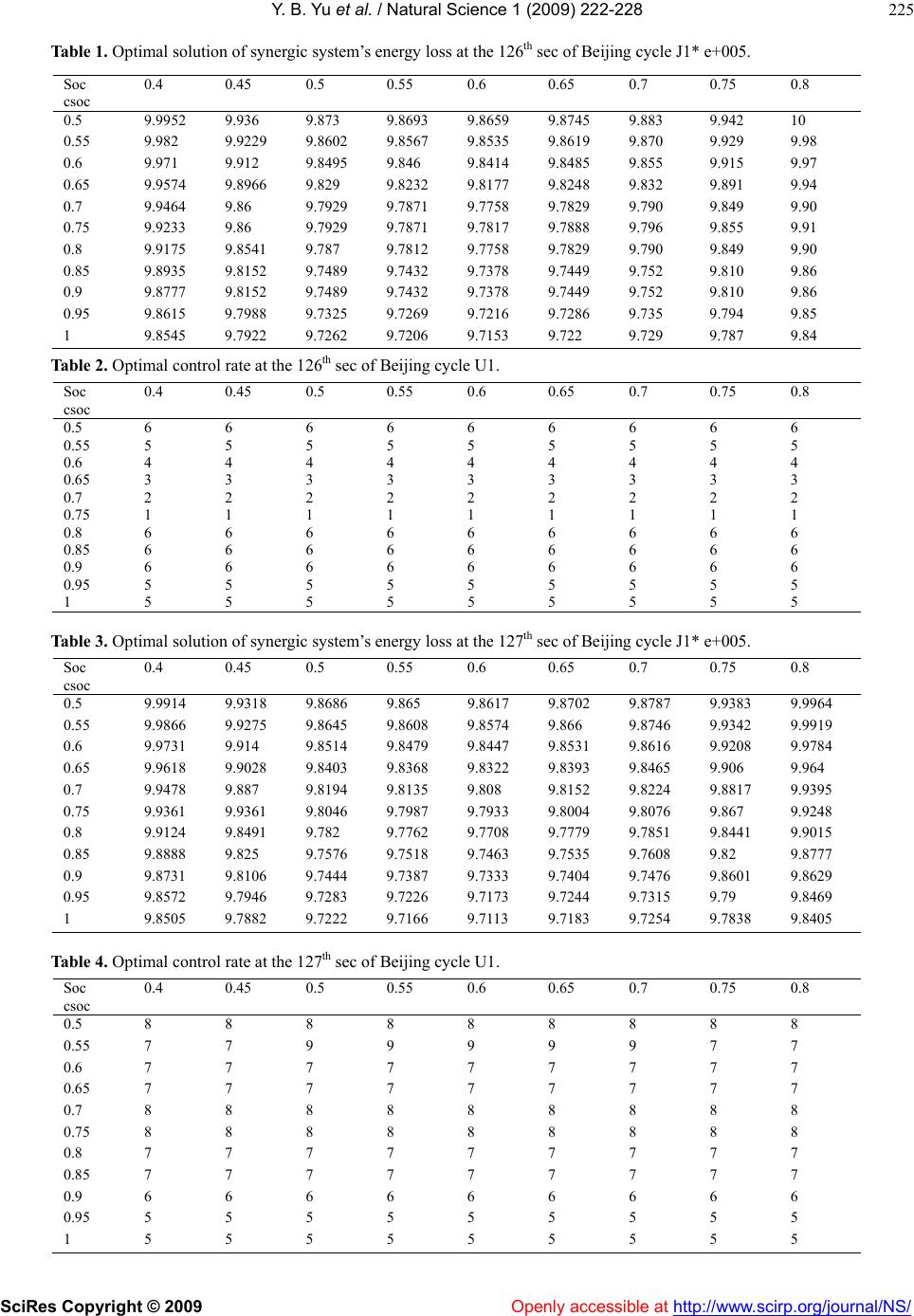

Y. B. Yu et al. / Natural Science 1 (2009) 222-228

225

Table 1. Optimal solution of synergic system’s energy loss at the 126th sec of Beijing cycle J1* e+005.

Table 2. Optimal control rate at the 126th sec of Beijing cycle U1.

Soc

csoc

0.4 0.45 0.5 0.55 0.6 0.65 0.7 0.75 0.8

0.5 6 6 6 6 6 6 6 6 6

0.55 5 5 5 5 5 5 5 5 5

0.6 4 4 4 4 4 4 4 4 4

0.65 3 3 3 3 3 3 3 3 3

0.7 2 2 2 2 2 2 2 2 2

0.75 1 1 1 1 1 1 1 1 1

0.8 6 6 6 6 6 6 6 6 6

0.85 6 6 6 6 6 6 6 6 6

0.9 6 6 6 6 6 6 6 6 6

0.95 5 5 5 5 5 5 5 5 5

1 5 5 5 5 5 5 5 5 5

Table 3. Optimal solution of synergic system’s energy loss at the 127th sec of Beijing cycle J1* e+005.

Soc

csoc

0.4 0.45 0.5 0.55 0.6 0.65 0.7 0.75 0.8

0.5 9.9914 9.9318 9.8686 9.865 9.8617 9.8702 9.8787 9.9383 9.9964

0.55 9.9866 9.9275 9.8645 9.8608 9.8574 9.866 9.8746 9.9342 9.9919

0.6 9.9731 9.914 9.8514 9.8479 9.8447 9.8531 9.8616 9.9208 9.9784

0.65 9.9618 9.9028 9.8403 9.8368 9.8322 9.8393 9.8465 9.906 9.964

0.7 9.9478 9.887 9.8194 9.8135 9.808 9.8152 9.8224 9.8817 9.9395

0.75 9.9361 9.9361 9.8046 9.7987 9.7933 9.8004 9.8076 9.867 9.9248

0.8 9.9124 9.8491 9.782 9.7762 9.7708 9.7779 9.7851 9.8441 9.9015

0.85 9.8888 9.825 9.7576 9.7518 9.7463 9.7535 9.7608 9.82 9.8777

0.9 9.8731 9.8106 9.7444 9.7387 9.7333 9.7404 9.7476 9.8601 9.8629

0.95 9.8572 9.7946 9.7283 9.7226 9.7173 9.7244 9.7315 9.79 9.8469

1 9.8505 9.7882 9.7222 9.7166 9.7113 9.7183 9.7254 9.7838 9.8405

Table 4. Optimal control rate at the 127th sec of Beijing cycle U1.

Soc

csoc

0.4 0.45 0.5 0.55 0.6 0.65 0.7 0.75 0.8

0.5 8 8 8 8 8 8 8 8 8

0.55 7 7 9 9 9 9 9 7 7

0.6 7 7 7 7 7 7 7 7 7

0.65 7 7 7 7 7 7 7 7 7

0.7 8 8 8 8 8 8 8 8 8

0.75 8 8 8 8 8 8 8 8 8

0.8 7 7 7 7 7 7 7 7 7

0.85 7 7 7 7 7 7 7 7 7

0.9 6 6 6 6 6 6 6 6 6

0.95 5 5 5 5 5 5 5 5 5

1 5 5 5 5 5 5 5 5 5

Soc

csoc

0.4 0.45 0.5 0.55 0.6 0.65 0.7 0.75

0.8

0.5 9.9952 9.936 9.873 9.8693 9.8659 9.8745 9.883 9.942 10

0.55 9.982 9.9229 9.8602 9.8567 9.8535 9.8619 9.870 9.929 9.98

0.6 9.971 9.912 9.8495 9.846 9.8414 9.8485 9.855 9.915 9.97

0.65 9.9574 9.8966 9.829 9.8232 9.8177 9.8248 9.832 9.891 9.94

0.7 9.9464 9.86 9.7929 9.7871 9.7758 9.7829 9.790 9.849 9.90

0.75 9.9233 9.86 9.7929 9.7871 9.7817 9.7888 9.796 9.855 9.91

0.8 9.9175 9.8541 9.787 9.7812 9.7758 9.7829 9.790 9.849 9.90

0.85 9.8935 9.8152 9.7489 9.7432 9.7378 9.7449 9.752 9.810 9.86

0.9 9.8777 9.8152 9.7489 9.7432 9.7378 9.7449 9.752 9.810 9.86

0.95 9.8615 9.7988 9.7325 9.7269 9.7216 9.7286 9.735 9.794 9.85

1 9.8545 9.7922 9.7262 9.7206 9.7153 9.722 9.729 9.787 9.84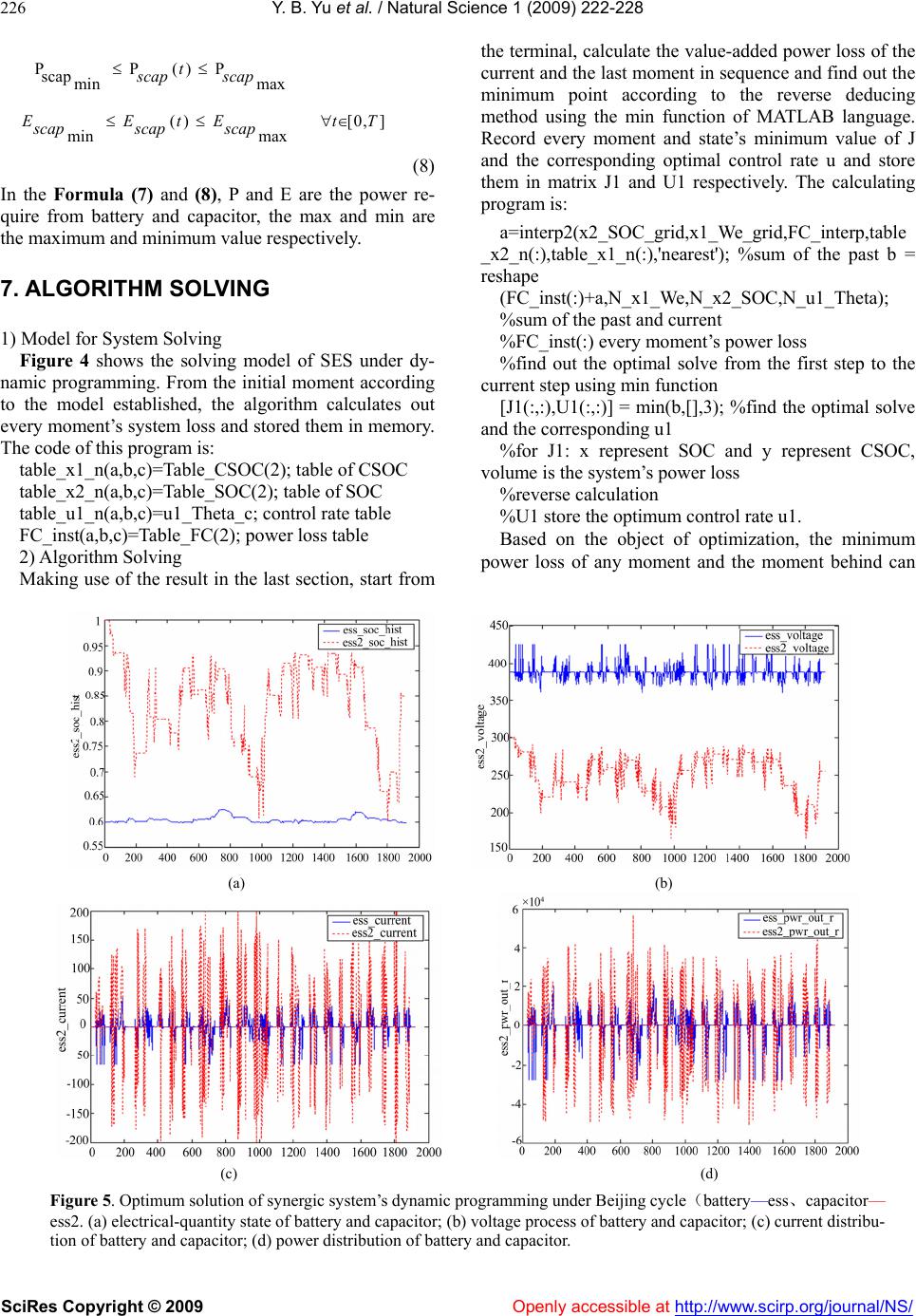

Y. B. Yu et al. / Natural Science 1 (2009) 222-228

226

PP()P

scap min max

()[0,]

min max

scap scap

EtE tT

scapscap scap



 

(8)

In the Formula (7) and (8), P and E are the power re-

quire from battery and capacitor, the max and min are

the maximum and minimum value respectively.

7. ALGORITHM SOLVING

1) Model for System Solving

Figure 4 shows the solving model of SES under dy-

namic programming. From the initial moment according

to the model established, the algorithm calculates out

every moment’s system loss and stored them in memory.

The code of this program is:

table_x1_n(a,b,c)=Table_CSOC(2); table of CSOC

table_x2_n(a,b,c)=Table_SOC(2); table of SOC

table_u1_n(a,b,c)=u1_Theta_c; control rate table

FC_inst(a,b,c)=Table_FC(2); power loss table

2) Algorithm Solving

Making use of the result in the last section, start from

the terminal, calculate the value-added power loss of the

current and the last moment in sequence and find out the

minimum point according to the reverse deducing

method using the min function of MATLAB language.

Record every moment and state’s minimum value of J

and the corresponding optimal control rate u and store

them in matrix J1 and U1 respectively. The calculating

program is:

a=interp2(x2_SOC_grid,x1_We_grid,FC_interp,table

_x2_n(:),table_x1_n(:),'nearest'); %sum of the past b =

reshape

(FC_inst(:)+a,N_x1_We,N_x2_SOC,N_u1_Theta);

%sum of the past and current

%FC_inst(:) every moment’s power loss

%find out the optimal solve from the first step to the

current step using min function

[J1(:,:),U1(:,:)] = min(b,[],3); %find the optimal solve

and the corresponding u1

%for J1: x represent SOC and y represent CSOC,

volume is the system’s power loss

%reverse calculation

%U1 store the optimum control rate u1.

Based on the object of optimization, the minimum

power loss of any moment and the moment behind can

(a) (b)

Figure 5. Optimum solution of synergic system’s dynamic programming under Beijing cycle（battery—ess、capacitor—

ess2. (a) electrical-quantity state of battery and capacitor; (b) voltage process of battery and capacitor; (c) current distribu-

tion of battery and capacitor; (d) power distribution of battery and capacitor.

Y. B. Yu et al. / Natural Science 1 (2009) 222-228

227

be calculated out under the reverse method and stored in

J1. At the same time, the optimum control rate is stored

in U1.Under Beijing cycle, the electrical power require-

ment of the 126th sec and the 127th sec is -16859w and

37467w. Table 1 to 4 list out the optimum solve J1 and

optimum control rate U1, and from which, the trend and

principle of controlling can be induced.

As is shown from the data, if the SOC and CSOC of

battery and super capacitor at some moment are known,

then the optimum solution J1 and optimum control rate

U1 can be checked up from tables above. After known

about the point’s power demand Pm and the optimum

control rate U1, the SOC and CSOC of battery and super

capacitor on the next moment can be calculated out

through every parts model, and then continue to look-up

tables to find out the optimum solution and optimum

control rate. Followed by analogy, on the situation when

the forward calculation mode. Connect every moment’s

optimal control rate, the optimum control rate of SES

under Beijing cycle can be drawn approximately. During

calculation, if the less interval of every component’s

state and control rate were used, the closer the result to

the synergic system’s optimal control rate.

In this way, under Beijing cycle, divide the battery’s

SOC from 0.4 to 0.8 into 9 parts. The interval of each

calculation point is 0.05. Divide the capacitor’s CSOC

from 0.5 to 1 into 11parts to ensure that the same inter-

val of calculation point is chose. After optimized calcu-

lation, the optimal control rate can be counted out shown

in Figure 5. Figure 5a illustrates the SOC of battery and

capacitor resulted from the optimized control under Bei-

jing cycle. Figure 5b shows the voltage process of bat-

tery and capacitor resulted from optimum control. Figure

(c&d) illustrate the current and power distribution re-

sulted from the optimum control rate at every moment

respectively.

3) Improved Rule-based Control Strategy

The result is based on cycle, so the Dynamic Pro-

gramming algorithm can be not directed applied to en-

gineering control. However, some enlightening can be

drawn used as the guidance of actual control algorithm

programming. For example, based on the result of pre-

vious section, the following four laws can be educed:

a).During power assisting, if the motor required a low

current, the battery would provide the power.

b).During power assisting, the capacitor should

provide more power when the motor is under high

power demand.

The two tips above are all induced by the low efficient

of DC/DC under low load.

c).If the capacitor is in high CSOC, and then it should

share a greater proportion of discharge. However, as the

CSOC drops, the discharge proportion of capacitor

would diminish responsively, while battery’s proportion

would increase gradually till the battery pack power the

motor alone.

d).When low-power braking, capacitor can recovery

all the vehicle braking energy; While, with the increase

of braking power, collaborative work mode of battery

and capacitor would be taken by the optimized control

algorithm to make the two both working on a high effi-

ciency and contribute to the balance of battery. Also the

proportion of discharge from capacitor would increase as

the braking power increase. This is different from the

rule of rule-based control strategy that energy firstly go

to the capacitor and it gives inspiration for the improve-

ment of control strategy.

Based on the analysis above, this section proposed a

modification on rule-based control strategy of SES when

motor power assisting and braking energy regeneration.

Details as follows:

(1) When power assisting, if Pm>0，and Pm<Pset ，

then Pbat=Pm;

(2) Otherwise, if Pm>Pset1，then Pscap=K1*Pm，but

Pbat=(1- K1) *Pm；in the formula: K1 is the function of

capacitor’s CSOC showed in table 5. Pset1=12.33kw.

(3) When braking: if P

m<0，and Pm>Pset2 ，

capacitor is not over recharged, then Pbat=0；otherwise

when Pm<Pset2，Pscap=K2*Pm, and Pbat=(1- K2) *Pm，K2

increases as Pm decreases.Pset2=8.7kw.

Figure 6 shows working process manipulate of SES’s

control rate, battery and capacitor resulted from the

simulation of rule-based control strategy, which is modi-

fied by applied optimal algorithm. Table 6 lists com-

parison of SES’s HEV simulation result under different

control algorithm. Conclusions can be drawn from the

various SES’s simulation results listed in the table, that

HEV vehicle have optimum fuel economy under control

of dynamic programming algorithm. Using the principle

of optimized DP algorithm, designer could know the

maximum energy-saving efficient contributed by SES

and also could compile optimal control algorithm of SES,

which can be used in actual engineering. Under this cir-

Table 5. Relationship between Ki and CSOC.

CSOC0.5 0.6 0.7 0.8 0.9 1.0

K1 0 0.2 0.4 0.6 0.8 1.0

Table 6. Simulation result comparison of synergic system.

Control strategyRule-based Dynamic

programming

Improved

rule-based

Fuel economy

（L/100km） 25.7 23.2 24.5

Fuel economy

improvement 1 ↑2.1% ↑1.6%

Power effi-

ciency 87% 93% 91%

Brake energy

recovery effi-

cient

8.34% 9.74% 9.35%

Y. B. Yu et al. / Natural Science 1 (2009) 222-228

228

Openly accessible at

(a)

(b)

Figure 6. Simulation result based on the optimized

rule-based control strategy under Beijing cycle; (a)

SOC,current and voltage of battery; (b) CSOC, current

and voltage of capacitor.

cumstance,capacitor can keep appropriate power state at

anytime and make vehicle fuel consumption a further

reduction. All the advantages above can prove the sig-

nificance improvement by dynamic programming opti-

mization algorithm

8. CONCLUSIONS

1) Dynamic programming algorithm had been applied to

SES to find out the optimum control rate using off-line

simulation.

2) Rule-based control algorithm was established based

on the optimum control rate. The simulation results

demonstrated that the method is practical and effective.

3) Based on the control rules of overall optimized al-

gorithm, the rule-based control strategy of the SES had

been improved and the control effect had also been

evaluated. The dissertation explicated the best perform-

ance and most efficient control method of SES which

could make the best contribution to vehicle energy-saving.

4) The overall optimized principle was suitable for the

programming and optimizing of control algorithm for

HEV vehicle with multi-energy power source.

REFERENCES

[1] T. Markel, M. Zolot, K. B. Wipke, and A. A. Pesaran,

(2003) Energy storage system requirement for hybrid

fuel cell vehicles. Advanced Automotive Battery Con-

ference, Nice, France, June. 10-13.

[2] A. C. Baisden and A. Emadi, (2004) ADVISOR-based

model of a battery and an ultra capacitor energy source

for hybrid vehicles. IEEE Transactions on Vehicular

Technology, 53(1).

[3] Y. B. Yu and Q. N. Wang, (2005) The redevelopment of

synergy electric power HEV simulation software based

on advisor. Jilin Daxue Xuebao (Gongxueban) /Journal

of Jilin University (Engineering and Technology Edition),

35(4), 353-357.

[4] Y. B. Yu and W. H. Wang, (2007) The research on fuzzy

logic control strategy of synergic electric system of hy-

brid electric vehicle. SAE Internatioal, 07APAC-185.

[5] D. P. Bertsekas, (1995) Dynamic programming and op-

timal control, Athena Scientific.

[6] J. M. Kang, I. Kolmanovsky, and J. W. Grizzle, (1999)

Approximate dynamic programming solutions for lean

burn engine aftertreatment. proceedings of the IEEE

conference on decision and control, 2, Piscataway, NJ,

1703-1708.

[7] C. Lin, J. Kang, J. W. Grizzle, and H. Peng, (2001) En-

ergy management strategy for a parallel hybrid electric

truck. Proceedings of the 2001 American Control Con-

ference, Arlington, VA, 2878-2883.

[8] M. P. O’Keefe and T. Markel, (2006) Dynamic pro-

gramming applied to investigate energy management

strategies for a plug-in HEV. The 22nd International Bat-

tery, Hybrid and Fuel Cell Electric Vehicle Symposium

and Exhibition (EVS-22), Yokohama, Japan, October

23–28.

[9] L. V. P´erez and G. R. Bossio, (2006) Optimization of

power management in an hybrid electric vehicle using

dynamic programming. Mathematics and Computers in

Simulation, 73, 244–254.