Journal of Intelligent Learning Systems and Applications
Vol.5 No.4(2013), Article ID:40069,7 pages DOI:10.4236/jilsa.2013.54030
Preliminary Study on Selling Tickets in Reason for Last Trains on Beijing Rail Transit Network
![]()
1State Key Laboratory of Rail Traffic Control & Safety, Beijing Jiaotong University, Beijing, China; 2School of Traffic and Transportation, Beijing Jiaotong University, Beijing, China; 3Beijing Metro, Beijing, China.
Email: lmjia@bjtu.edu.cn, jialm@vip.sina.com
Copyright © 2013 Yang Wang et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received May 30th, 2013; revised June 30th, 2013; accepted July 7th, 2013
Keywords: Intelligent Transportation; Urban Rail Transport Network; Automatic Ticketing System; The Last Train; Transfer
ABSTRACT
With the increase of Beijing urban rail transport network, the structure of the road network is becoming more complex, and passengers have more travel options. Together with the complex paths and different timetables, taking the last train is becoming much more difficult and unsuccessful. To avoid losses, we propose feasible suggestions to the last train with reasonable selling tickets system.
1. Introduction
In the urban mass transit network [1], poor service time connections of the last trains, long transfer distance, inconvenient transfer and other factors [2] often lead to the embarrassing situations that passengers cannot arrive the destination after one or more transfer though they have tickets, because the needed lines have already stopped operations. This is not only a waste of time, but also an economic loss. With the development of the network and the complexity of the transferred path, the unsuccessful transfers are becoming increasingly common [2].
In accordance with the situation that the passengers with tickets cannot catch the last train in the urban mass transit network, this paper puts forward some suggestions on the reasonable ticketing of the last train, in order to ensure the accessible paths and humanized services.
2. Basic Conception
2.1. Transfer
Urban rail Transfer is referred to behaviors that passengers transfer between the lines or different transportation modes. It mainly contains three types: the Transfer between lines, Transfer between rail transit and public transportation, for instance bus, car and bicycle, etc. It refers in particular to the Transfer between lines.
2.2. Transfer Mode
Transfer mode is divided into 5 kinds: Cross Platform Transfer, Node Transfer, Hall Transfer, Channel Transfer, and Offsite Transfer, along with 5 kinds of corresponding basic forms: Parataxis, Determinant, Cross, Type T and Type L [3].
Table 1 shows the examples of representative stations and lines those are of different Transfer modes in Beijing Metro.
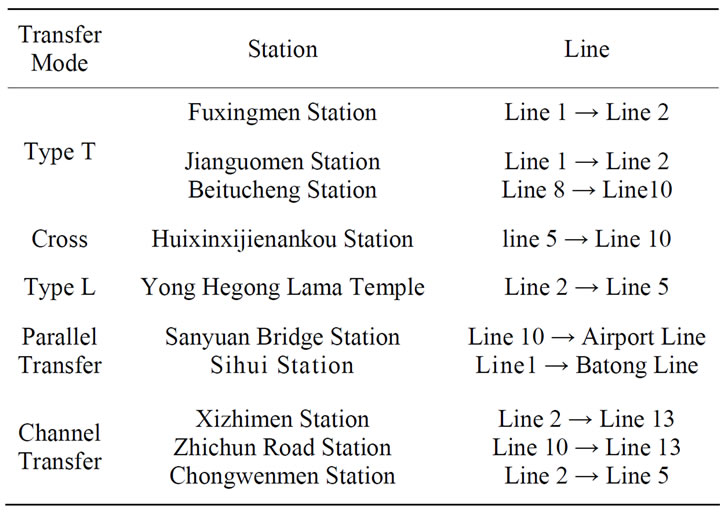
Table 1. Examples of the transfer station types and lines in Beijing railways.
3. Facility
At present, the subway platforms are often connected with transfer channels, station halls and other platforms by stairs. Each platform is connected by two or more stairs. The layouts of the stairs contain two-terminal, centralized and distributed.
Different Transfer modes lead to different Transfer facilities, as showed in the Table 2.
Actually, the station always adopts multi-Transfer modes, not single one type.
4. Model
4.1. Last Train Model
4.1.1. Network Topology Model
After analytical investigations of the network and distribution characteristics of the stations and lines, a network of urban rail transport is proposed that the station can be regarded as a node, the sections between two stations as an edge and the running time in sections as the weight, in this way the network topology can be described as 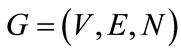 [4]. Accessibility principle of last train is: if passengers can Transfer successfully at one Transfer station of lines, this path can be thought as OD accessibility; if the last between two Transfer stations is accessible, passengers can reach any station within this section from the Transfer station.
[4]. Accessibility principle of last train is: if passengers can Transfer successfully at one Transfer station of lines, this path can be thought as OD accessibility; if the last between two Transfer stations is accessible, passengers can reach any station within this section from the Transfer station.
The Figure 1 shows the simplified network topology model 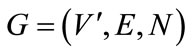 .
.  stands for the key stations: both Transfer station and initial/terminal station
stands for the key stations: both Transfer station and initial/terminal station 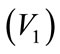 , Transfer station
, Transfer station 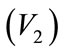 , initial station and terminal
, initial station and terminal  . The node is defined by three-digit number, the first number is the level of the node, and the other two are the node number in this level.
. The node is defined by three-digit number, the first number is the level of the node, and the other two are the node number in this level.
According to the figure 1, 0 - 1 matrix is set up, the connected relations between two nodes are showed as follows.
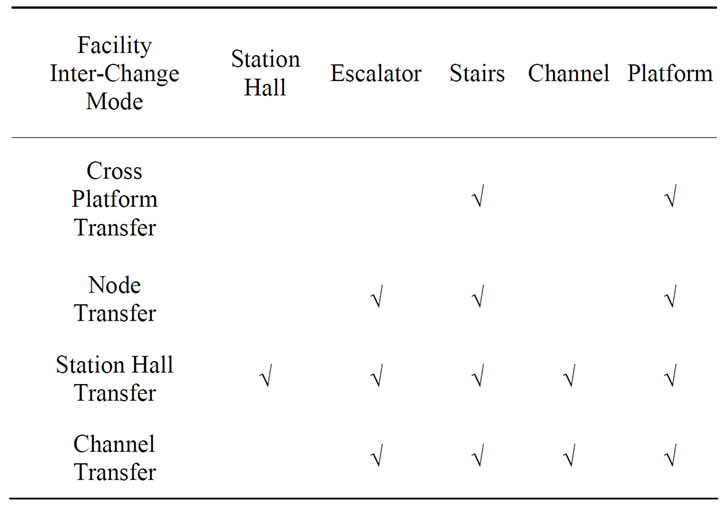
Table 2. Different transfer modes and facilities.
 (1)
(1)
As space is limited, Figure 2 shows 0 - 1 matrix of partial network.
According to the relations of nodes, the reachable set between two nodes can be easily searched, as well as the weigh matrix between nodes. Thus, we can make a comparison between the lengths of each path, and search for the shortest path and the next shortest path. The selected path may not be the optimal Transfer plan, waiting time and other factors need to be deeply synthesized, otherwise the destination may not be reached.
4.2. Transfer Time Model
When calculating passengers’ walking time of the Transfer path, the Transfer time is needed to be considered apart from the last train’s time of the initial station and Transfer station.
4.2.1. Travel Process
Figure 3 shows the travel process, it contains getting in station, buying tickets, security checks, ticket checking, waiting, and getting on trains. Ticketing is not necessary, as passengers with IC cards can go through the security checks directly. For the same station, the walking time of passengers get in the station differs in different entrances.
4.2.2. Walking Time
The waiting time of passengers 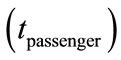 starts from buying tickets, it contains time of buying tickets
starts from buying tickets, it contains time of buying tickets  , security checks
, security checks  , tickets checking
, tickets checking  and waiting
and waiting 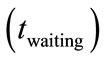 . During the whole process, the walking time those passengers go through the facilities
. During the whole process, the walking time those passengers go through the facilities  like escalator
like escalator  , stairs
, stairs 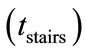 , channel
, channel  and platform
and platform  . So, the formula of walking time is
. So, the formula of walking time is
 (2)
(2)
The  is given by
is given by
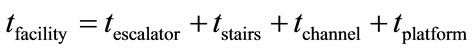 (3)
(3)
As walking speed differs in different people, the additional time is introduced for the sake of making the connections of last trains more rational and more reliable.
 (4)
(4)
1) Walking timing on escalators
 (5)
(5)
where a is the number of the escalators, n is the total of all escalators. ta is the walking time on ath escalator, La is
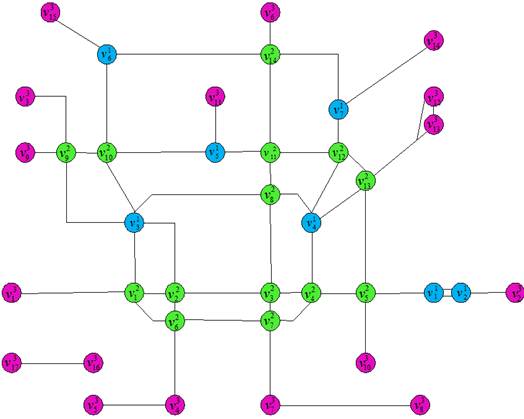
Figure 1. the topology structure chart of the simplify model.

Figure 2. the 0 - 1 matrix of partial network.

Figure 3. Passenger travel flowchart.
the length of ath escalator, and va is the ath escalator speed, the value is 0.65 m/s.
2) Walking timing on stairs
 (6)
(6)
where b is the number of the upward escalators, n is the total of all upward escalators. tb is the walking time on bth stairs, Lb is the length of each stairs, and vb is the walking speed on the bth stairs. c is the number of the downward escalators.
3) Walking timing in channels
 (7)
(7)
where d is the number of the channels, n is the total of all channels. td is the walking time in bth channel, Ld is the length of bth channel, and vd is the passengers’ walking speeds in bth channel.
4) Walking timing on platform
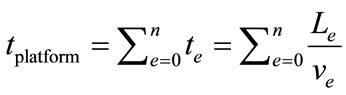 (8)
(8)
where e is the number of the platforms, n is the total of all platforms. te is the walking time on bth platform, Le is the length of bth platform, and ve is the passengers’ walking speeds on bth platform.
5. Reasonable Ticket-Selling Algorithm of Last Train
5.1. Rule
5.1.1. Non-Transfer Path
The judgment is whether the last train of this path can be reached in the initial station.
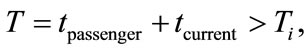
T value is the sum of the walking time and current time.
5.1.2. Transfer Path
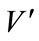 is the set of key Transfer stations,
is the set of key Transfer stations, 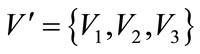 .
. 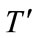 is the set of departure time of key Transfer stations,
is the set of departure time of key Transfer stations,  . T is the set of the time of passengers arriving on the platform,
. T is the set of the time of passengers arriving on the platform, 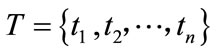 . T contains Transfer time. When
. T contains Transfer time. When 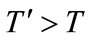 , the passengers can Transfer successfully.
, the passengers can Transfer successfully.
5.1.3. Path with Loop Line
The table below is the last train timetable [5] of Beijing Subway Line 2.
As shown in Table 3, there are two kinds of last train. The first kind is that the train runs the whole line, and the second is the local train.
1) Outer-Ring Train Last train runs the direction from Xizhimen (22:14) to Jishuitan (22:55). And after one whole trip back to Xizhimen (22:59), the train goes into the yard.
2) Inner-Ring Train Last train runs the direction from Jishuitan (21:55) to Xizhimen (22:41). And after one whole trip back to Xizhimen (22:45), the train goes into the yard.
So we should presume several kinds of situation: A is the starting station (Xizhimen) of Line 2, S and T is passenger’s origin and destination respectively. Thus fol
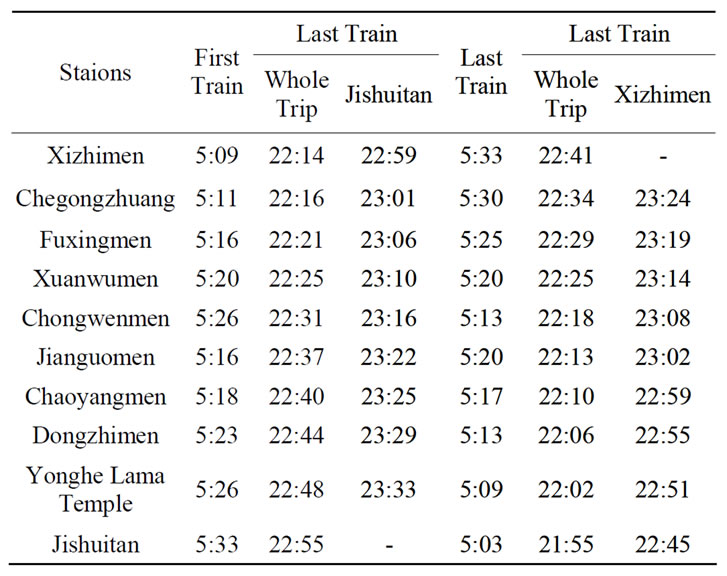
Table 3. Partial timetable of last train of line 2 in Beijing subway.
lowing are the three cases:
1) S and T on the loop line a) The path does not contain Xizhimen or Jishuitan, with no Transfer. Passengers only need to catch the last train in time.
b) When the path contains Xizhimen or Jishuitan, passengers need to determine which direction he/she should take, which depends on whether the train goes back to yard or not.
2) S or T on the loop line In this situation, passengers need to transfer at a certain Transfer station of the loop line.
a) When the path does not contain Xizhimen or Jishuitan, passengers only need to make sure of the last train timetable of the Transfer station.
b) When the path contains Xizhimen or Jishuitan, passengers only need to determine which direction he/she should take, which depends on the train and the Transfer station timetable.
3) Neither of S and T on the loop line In this situation, passengers need to transfer at Transfer station A and B of the loop line.
a) When the path does not contain Xizhimen or Jishuitan, passengers only need to make sure of the last train timetable of A and B.
b) When the path contains Xizhimen or Jishuitan, passengers should get on the train at Station A when the train he/she takes will complete the whole trip, then get off at Station B, and continue to take another line.
5.2. Selection Method of Optimal Path
According to the Dijkstra algorithm [6,7], the research emphasis is turned into a search for the shortest time of path, namely calculating the shortest Transfer path from a certain station to destination with short-path algorithm. The description method is described as follows:
1) First, gain the time weight 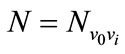 from initial station to each stations,
from initial station to each stations, 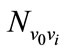 is running time between sections (v0, vi). If (v0, vi) is nonexistent, then set Noi for +∞, S is the set of terminals of shortest paths from station v0, the initial state is empty set. Then initial values of the shortest path from the initial station to all the other stations vi are
is running time between sections (v0, vi). If (v0, vi) is nonexistent, then set Noi for +∞, S is the set of terminals of shortest paths from station v0, the initial state is empty set. Then initial values of the shortest path from the initial station to all the other stations vi are

where v is the set of initial stations.

2) Choose station vj, then let

where vi comes from vi, to the terminal of the shortest path, and 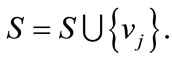
3) Modify lengths of the shortest reachable paths from the initial station to any stations in the set V - S. If
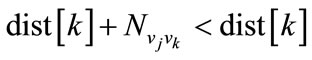
then
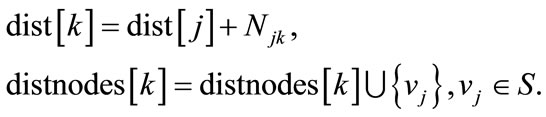
4) Repeat step 2 and step 3, (n - 1) times. Then, shortest path from v0 to other stations is gained.
6. Process Flow and Interface of System
To realize the function, the following systems are needed: AFC, TCC and GATE. These three systems don’t link to each other at present. That means, they are in the information isolation. The system designed in the paper can connect the 3 systems in order to share information. The remaining time after passengers take the last trains successfully can be judged according to the last train operation plan and adjustment plan controlled by TCC. When the remaining time reaches a specified value (slack time, lest the passengers are affected by other passengers and personal differences), TVMs stop ticketing and passengers who have gone through security can’t get into the stations. By this way, passengers can avoid unnecessary economic loss and a waste of time.
Process flow of the system is shown in Figure 4. Figure 5 shows the system function interface.
If the destination cannot be reached, passengers cannot purchase tickets, AFC will remind passengers that the destination is unreachable and suggest them to go to the adjacent stations. Thus this can avoid the unreachable situations and provide more options for travelers.
Apart from the AFC, the GATEs display the stop signal when passengers with IC cards, remind the passengers cannot get in the stations.
7. Conclusions
We proposed the preliminary idea of the reasonable ticketing of last train due to the lack of this function type in Beijing Metro. Combined with the network and timetable of last trains, the application scheme is carried out and Beijing Metro last train Transfer inquiry system is preliminarily designed.
This idea is beneficial to settle the reasonable ticketing of last train, promote the operation benefit and service level of urban rail transit, and reduce or avoid the situations that destinations are unreachable and passengers cannot get in the stations.
8. Acknowledgements
This work has been supported by China National Tech-
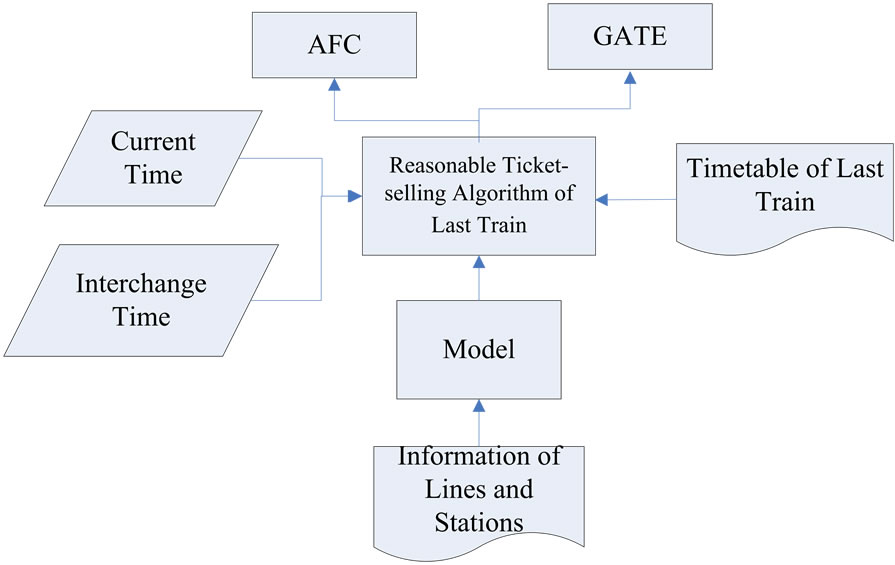
Figure 4. System flow chart.
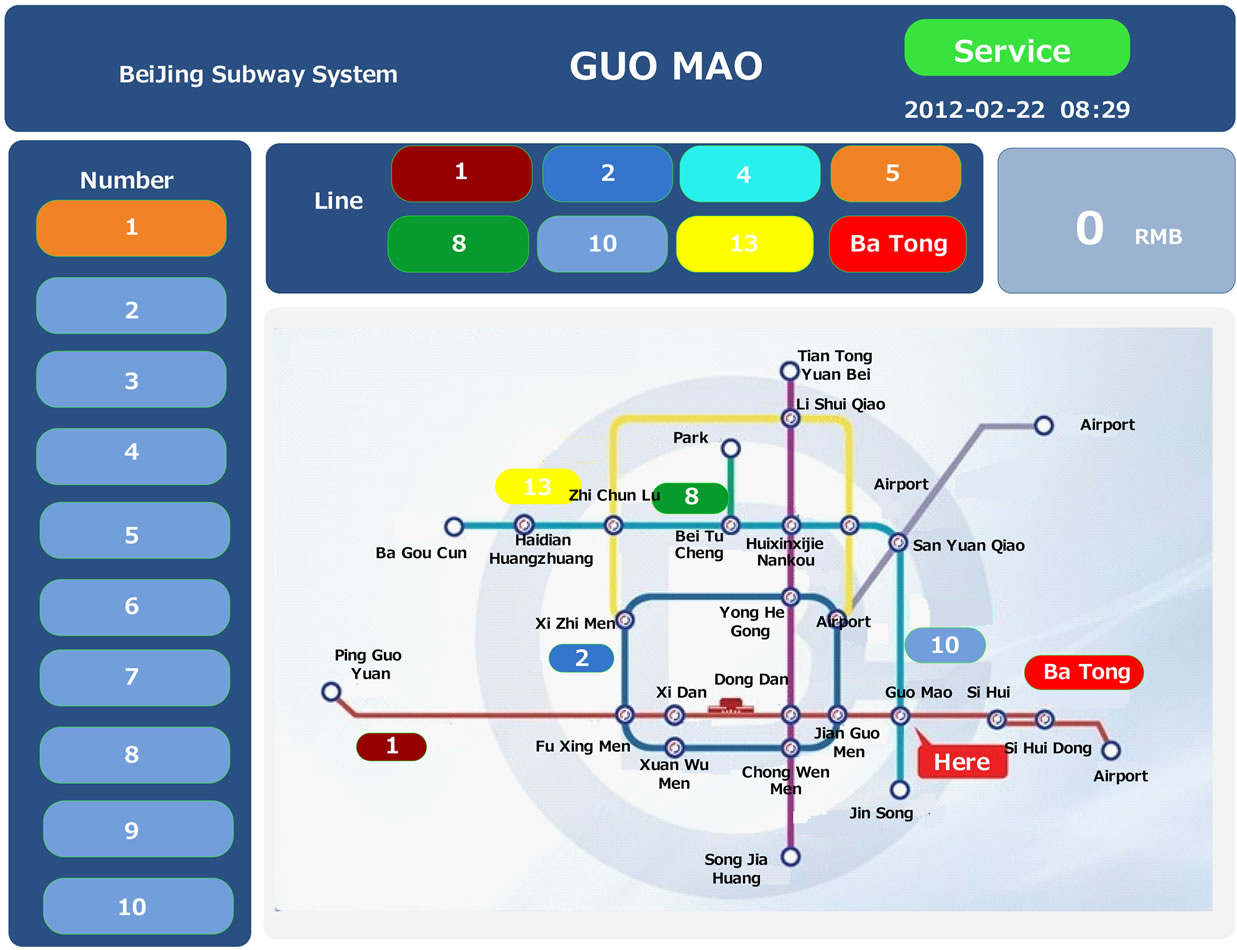
Figure 5. System function interface.
nique Supporting Plan Project (Grant: 2008BAG 11B01), National Natural Science Project (Grant: 61074150) and National Key Technology Research and Development Programs (2011BAG01B02).
REFERENCES
- Y. Yuan, “Design and Realization of Subway Terminal Monitoring Equipment System,” Nanjing University of Science and Technology, Nanjing, 2013.
- Y. B. Peng, “Study and Application of an Algorithm of Selling Tickets in Reason for Last Train on Rail Transit Network,” Donghua University, Shanghai, 2010.
- Code for Design of Metro (GB50157-2003).
- X. F. Wang, X. Li and G. R. Chen, “Complex Network Theory and Applications,” Tsinghua University Press, Beijing, 2006.
- http://www.bjsubway.com/e/action/ListInfo/?classid=39&ph=1&station=%C6%BB%B9%FB%D4%B0#
- F. X. Wang, “Dijkstra Algorithm in the Intelligent Public Transport Query System,” Wuhan Polytechnic University, Vol. 29, No. 2, 2010, pp. 59-62, 70.
- E. W. Dijkstra “A Note on Two Problems in Connexion with Graphs,” Numerische Mathematik, Vol. l, No. 1, 1959, pp. 269-271. http://dx.doi.org/10.1007/BF01386390

