Journal of Water Resource and Protection
Vol.08 No.03(2016), Article ID:65180,14 pages
10.4236/jwarp.2016.83033
Application of SWAT Model to the Olifants Basin: Calibration, Validation and Uncertainty Analysis
Charles Gyamfi1,2*, Julius Musyoka Ndambuki1, Ramadhan Wanjala Salim1
1Department of Civil Engineering, Tshwane University of Technology, Pretoria, South Africa
2School of Bio-Resources Engineering, Anglican University College of Technology, Nkoranza, Ghana

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 2 September 2015; accepted 27 March 2016; published 30 March 2016
ABSTRACT
The application of the Soil and Water Assessment Tool (SWAT) to the Olifants Basin in South Africa was the focus of our study with emphasis on calibration, validation and uncertainty analysis. The Basin was discretized into 23 sub-basins and 226 Hydrologic Response Units (HRUs) using 3 arc second (90 m × 90 m) pixel resolution SRTM DEM with stream gauge B7H015 as the Basin outlet. Observed stream flow data at B7H015 were used for model calibration (1988-2001) and validation (2002-2013) using the split sample approach. Relative global sensitivity analysis using SUFI-2 algorithm was used to determine sensitive parameters to stream flow for calibration of the model. Performance efficiency of the Olifants SWAT model was assessed using Nash-Sutcliffe (NSE), coefficient of determination (R2), Percent Bias (PBIAS) and Root Mean Square Error-Observation Standard deviation Ratio (RSR). Sensitivity analysis revealed in decreasing order of significance, runoff curve number (CN2), alpha bank factor (ALPHA_BNK), soil evaporation compensation factor (ESCO), soil available water capacity (SOIL_AWC, mm H2O/mm soil), groundwater delay (GW_ DELAY, days) and groundwater “revap” coefficient (GW_REVAP) to be the most sensitive parameters to stream flow. Analysis of the model during the calibration period gave the following statistics; NSE = 0.88; R2 = 0.89; PBIAS = −11.49%; RSR = 0.34. On the other hand, statistics during the validation period were NSE = 0.67; R2 = 0.79; PBIAS = −20.69%; RSR = 0.57. The observed statistics indicate the applicability of the SWAT model in simulating the hydrology of the Olifants Basin and therefore can be used as a Decision Support Tool (DST) by water managers and other relevant decisions making bodies to influence policy directions on the management of watershed processes especially water resources.
Keywords:
Calibration, Validation, Uncertainty Analysis, Olifants Basin, SWAT Model

1. Introduction
Like many other basins in the world [1] - [4] , the Olifants Basin in South Africa is faced with challenging watershed issues ranging from water quantity, quality and the influence of anthropogenic activities on available water resources [5] . These watershed problems have over the years increasingly gained global attention owing to the fact that water resources are professed to be the pivot for which developmental agenda and improvement in livelihoods can be achieved [6] . Others [7] [8] have suggested that for improvements in livelihood in terms of poverty reduction, livelihood empowerment and long term economic growth to be attained, then there would be the need to have access to freshwater that meets both quantity and quality demands. More importantly, also, is the fact that issues of water are now perceived to be of national and regional security risks [9] . As water resources diminish due to population growth, pollution and over exploitation, the competition for water will continually exacerbate which is seen as a potential source of conflict [10] - [12] . In line with meeting the water supply needs of man and the ecosystem, a new paradigm shift for water resources planning has therefore been suggested [13] [14] .
To effectively plan for water resources and mitigate against existing watershed problems calls for a clear understanding and insight into prevailing watershed processes in order to spearhead planning and implementation of appropriate control measures. One of such ways has been the application of tools such as hydrologic models, water quality models and geographic information systems which have proven versatile in the acquisition of knowledge in line with watershed processes [15] . However, the use of tools such as hydrologic models presents some difficulties due to the large number of parameters involved in the hydrologic modeling process coupled with measurement errors in model inputs [16] [17] . For a hydrologic model to be reliable in the planning processes it is required that resulting uncertainty in its application be curtailed within the barest allowable range through a reliable calibration and validation procedure. In view of this, we present in this work an outlook on the application of the Soil and Water Assessment Tool (SWAT) a semi distributed hydrologic model to simulate the stream flow of the Olifants Basin with emphasis on 1) identification of sensitive parameters to stream flow; 2) calibration and validation of the model for stream flow for the study basin; and 3) an assessment of model performance. The objects of the study were to test the applicability of the SWAT model to the Olifants Basin and to examine its potential as a decision support tool for water managers and policy makers.
The Soil and Water Assessment Tool (SWAT) is a physically based medium to large scale river basin model developed by the Agricultural Research Service of the United States Department of Agriculture (USDA-ARS) [18] . The basic operational unit of the SWAT model is the hydrologic response units (HRUs) which consist of an area of homogenous land use, topography and soil characteristics. The concept of HRUs is to cater for the diverse ways by which different land use and soil types impacts on hydrology of a watershed. Since its introduction, SWAT has been used in diverse applications ranging from water resources planning, investigation into hydrological processes, water quality modeling and climate change studies [19] - [22] . For details on the SWAT model one is referred to Neitsch et al. [23] .
2. Materials and Methods
2.1. Study Area
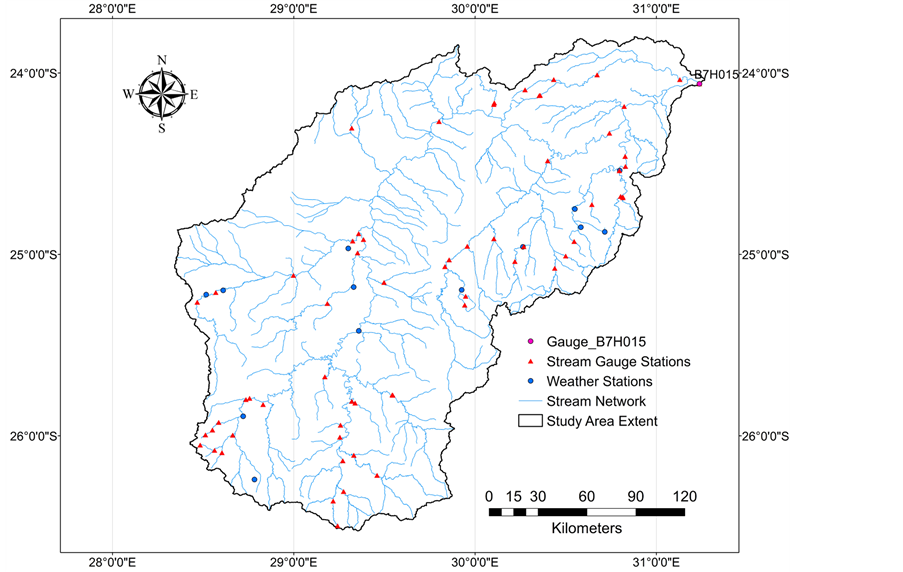
The Olifants Basin was used as the case study due to the socio-economic recognition of this basin to the South African economy but however reported to be water stressed calling for an effective action of water resources planning and management. The Olifants basin which is divided into two by an escarpment is located in the north-eastern part of South Africa (Figure 1). Geographically, it is bordered by latitudes 23.8˚S and 26.5˚S and longitudes 28.3˚E and 31.9˚E. It traverses three provinces in South Africa namely, Gauteng, Mpumalanga and Limpopo where it finally enters into Mozambique. The Olifant River with a main stem of approximately 770 km in length drains a total land surface area of 54,308 km2 [24] . The River originates from Trichardt to the east of Johannesburg in the province of Gauteng and then flows in the north-eastern direction through the provinces of Mpumalanga and Limpopo. The Olifant River crosses the Mozambique border and flows into the Massingire dam. The main tributaries of the Olifant are the Wilge, Moses, Elands and Ga-Selati rivers on the left bank and Klein Olifant, Steelpoort and Blyde rivers on the right bank [25] . On the right bank, steelpoort is the largest tributary draining an area of 7136 km2 compared to the Elands on the left bank with a drainage area of 6148 km2. Generally, the elevation of the basin ranges from 0 - 2400 meters above mean sea level (masl). Climatically, the
Figure 1. Location of the Olifants Basin.
basin is characterized by the movement of air masses that is known to be associated with Inter-Tropical Convergence Zone (ITCZ). In summer, temperatures range from a minimum of 18˚C to a maximum of 34˚C whereas in winter temperatures ranges from 5˚C to 26˚C [25] . Rainfall is seasonal in the basin, occurring during the months of October to April with appreciable spatio-temporal variability. The mean annual precipitation (MAP) is documented by Schulze et al. [26] to be 630 mm with peaks in January.
2.2. Scope of the Study
The scope of the study as inferred in this work refers to the section of the Olifants Basin upstream of the stream gauge station B7H015. This section of the basin drains a total area of 50,024 km2. The remaining section of 4, 200 km2 downstream of gauge B7H015 was not included in this study. As the focus of the study was on calibrating and validating the SWAT model, it was imperative therefore to select a reliable stream flow gauge station for calibration and validation purposes hence the selection of gauge B7H015 with considerable data from 1980-2013.
2.3. Data Sources
2.3.1. Hydro-Meteorological Data
From the Department of Water Affairs (DWA), South African Weather Service (SAWS) and the Climate Forecast System Reanalysis (CFSR) database, climatic variables inclusive of maximum and minimum temperature, rainfall, solar radiation, wind speed and humidity were acquired. These variables served as the atmospheric parameters used in driving the hydrologic simulation of the study watershed. Meteorological stations were selected if they satisfied the criterion of not having more than 10% missing data. Based on the set criteria and taking into cognizance the time span, 13 meteorological stations were finally selected for use (Figure 2). With the exception of meteorological station 04774946, all the other stations had varying degree of missing data which were patched prior to using in the hydrologic simulations. Stream flow gauge readings were also acquired from DWA for model calibration and validation.
2.3.2. Soil Data
Soil physico-chemical and hydrological properties were obtained from various FAO-UNESCO soil databases
Figure 2. Hydro-meteorological stations within the study area.
[27] [28] . The soil databases contains attributes for each soil polygon, namely, soil texture, Hydrological Soil Group (HSG), soil depth, rock fragments and organic carbon content and these databases are considered the single most comprehensive available resource with vast database on soil attributes for Africa and the world [29] .
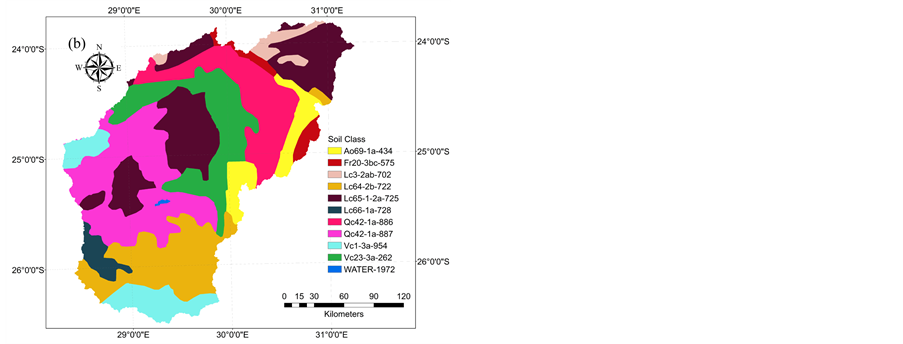
A subset of the soil map for the study area showed five major soil types. Presented in Table 1, are the major soil types with some selected physical and hydrological properties that were used in the study. All the attributes of the soils (soil texture, Hydrological Soil Group (HSG), soil depth, rock fragments and organic carbon content) were captured into a database using GIS which provided a link for usage in SWAT. The value fields that ensured the proper recall of gridded soil information were the serial number (SNUM) and the FAO soil code.
2.3.3. Land Use/Cover Data
Landsat 7 ETM/ETM + level 1 terrain corrected satellite images obtained from the Global Visualization Viewer (GloVIS) formed the basis for the execution of the land use and land cover classification component of the study. The images which are of spatial resolution 30 m, were obtained for Path/Row; 168/077, 169/077, 169/078, 170/077 and 170/078 for the period 2013. The images were classified into five-level 1 classes based on the land cover and land use classification system developed by Anderson et al. [30] for the interpretation of remote sensor data at various scales and resolutions.
2.4. Model Setup and Parameterization
Delineation of the study watershed (Figure 3) was done in Arc SWAT using the automatic watershed delineator with a 3 arc second (90 m × 90 m) pixel resolution SRTM DEM. The SRTM DEM version 4 which was released by the Consortium for Spatial Information of the Consultative Group of International Agricultural Research (CGIAR-CSI) was selected for use due to its significant improvements over previous versions. Watershed delineation was guided by the procedures used by Neitsch et al. [31] . Stream gauge B7H015 was selected to be the outlet point of the watershed. This gauge station is located on the main-stem of the Olifants River. The selection of this gauge station was informed by the availability of stream flow data that exist for this gauge and as result deemed to be appropriate for model calibration and validation. The area of the delineated watershed was cut short of previously defined Olifants Basin due to the gauge station that was used in defining the watershed outlet.
Table 1. Physical and hydrological properties of major soils in the Olifants Basin.
BD, bulk density; AWC, available water content, *Average for layer 1 and 2 of soil profile.
Figure 3. Discretization layout of the Olifants Basin using gauge B7H015.
The watershed was discretized into a total of 23 sub-basins with the smallest draining an area of 45 km2 and the largest an area of 6681 km2. Total drainage area of the delineated watershed was 50,024 km2 with the main stem of the Olifants traversing a distance of 626 km. A comparison of the delineated Olifants Basin used in this study to that already existing revealed a drainage area difference of approximately 4200 km2. This section of the Olifants located downstream of the delineated watershed was not considered in this study.
2.4.1. Slopes and HRU Definition
Slopes discretization of the Olifants watershed was guided by the classification used by FAO [32] . Based on this, the study watershed was classified to have three slope classes namely; level to gently undulating (<8%), rolling to hilly (8% - 30%) and steeply dissected to mountainous (>30%). The multiple slope classes approach was used to cater for the different slopes that exist within the area unlike using a single slope approach.
In defining the HRU, an overlay analysis of the land use, soils and slopes were carried out and a unique combination of a particular type of land use, soils and slopes were then grouped to form an HRU. The HRU relying on the distinct characteristics of land use, soils and slopes of the watershed forms the premise for the prediction of watershed processes. To account for complex watershed processes without undue attention for minor physiographic features, multiple HRUs with threshold definitions of 10%, 10%, 10% for land use, soils and slopes were used respectively. The implication of the threshold value is to eliminate in the generation of the HRUs all areas with coverage less than the stipulated HRU threshold. In doing so, the model simulates for watershed processes based on the substantive land use, soils and slopes within in the watershed.
2.4.2. Parameter Sensitivity Analysis
As watershed processes are influenced by a large number of parameters, sensitivity analysis was performed using the Sequential Uncertainty Fitting (SUFI-2) algorithm to identify the key parameters that affect stream flow for calibration. The global sensitivity analysis approach which considers the sensitivity of one parameter in relation to other parameters under consideration was used to determine the sensitive parameters in this study [33] . The t-stat which gives a measure of the sensitivity of a parameter and the p-value, the significance of the sensitivity of that parameter were used to rank the various parameters considered to influence stream flow. From other studies the listed parameters in Table 2 were discovered to be sensitive to stream flow [34] [35] . However, these parameters vary from one watershed to the other depending on prevailing geomorphologic characteristics and activities existing in a watershed and therefore cannot assume generalization status. In initializing the sensitivity analysis, the parameters listed in Table 2 were considered and the final parameters selected based on the t-stat and the p-value. Following sensitivity analysis, model calibration was done using the selected most sensitive parameters.
2.4.3. Model Calibration, Validation and Performance Evaluation
The complex processes occurring in watersheds coupled with the uncertainty inherent in hydrologic modeling parameters, inputs and measured data requires that hydrologic models be calibrated and validated to minimize predictive errors [35] . One of the most widely accepted algorithm; the Sequential Uncertainty Fitting (SUFI-2) which operates based on the Latin Hypercube sampling procedure was used to calibrate and validate the hydrologic setup [35] [36] . A split sample procedure using monthly stream flow data from stream gauge B7H015 for the period 1988-2001 and 2002-2013 were used for calibration and validation respectively. The first 8 years were used as warm up period to mitigate unknown initial conditions. As a result, the first 8 years were excluded from the analysis.
Table 2. Parameters considered in sensitivity analysis.
The SUFI-2 algorithm was operationalized within the SWAT calibration and Uncertainty Procedure (SWAT- CUP) environment. As suggested by Abbaspour et al. [36] several model simulations were executed with a minimum of 500 simulations in each run. Following each run, simulated results were compared with observed variables of interest and the performance of the model in simulating the observed variable judged against four objective functions. The choice of an objective function is dictated by the object of any particular study and hence there is no objective function that is universally applicable to all situations [37] . In this study however, efficiency measures including the Nash-Sutcliffe (NSE) [38] [Equation (1)], the coefficient of determination (R2) [8] [Equation (2)], percent bias (PBIAS) [39] [Equation (3)] and RMSE-observations standard deviation ratio (RSR) [39] [Equation (4)] were used to evaluate the performance of the model.
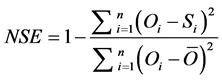 (1)
(1)
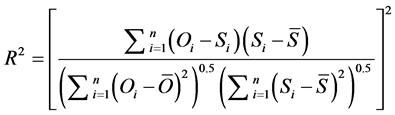 (2)
(2)
 (3)
(3)
 (4)
(4)
where;
Oi = observed variable, Si = simulated variable, 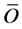 = mean of observed variable,
= mean of observed variable,  = mean of simulated variable, n = number of observations under consideration.
= mean of simulated variable, n = number of observations under consideration.
3. Results and Discussion
3.1. Characteristics of Discretized Watershed
Discretization of the Olifants watershed resulted in a total of 23 sub basins with 226 HRUs using land use, soil and slope thresholds of 10%, 10% and 10% respectively. Elevation ranges between 0 - 2328 m with a mean of 1220 m and a standard deviation of 378 m. Characteristics of the delineated watershed with respect to land use type, soils and slope is summarized in Figure 4 and Table 3. The land use characterization for 2013 based on the stated threshold values consisted mainly of range land (40.05%), agriculture (36.88%), residential (22.62%) and mixed forest (0.46%). Agriculture being the second largest land use type is in affirmation of the economic importance this area contributes towards the gross domestic product (GDP) of the South African economy. The distribution of soil types recorded chromic luvisols to be the most dominant soil with a total coverage of 38.81% of the watershed followed by cambic arenosols (33.03%) and chromic vertisols (21.21%). Orthic acrisols and rhodic ferralsols constituted a marginal proportion of 5.77% and 1.18% respectively. Slope classification following FAO slope classes indicated a larger proportion (76.57%) of the studied watershed having a level to gently undulating terrain within slope class <8%. Rolling to hilly terrain (slope class 8% - 30%) constituted 18.26% with the remaining 5.17% of the area being steeply dissected to mountainous (slope class >30%). Inference from the classified slopes generally portrays that the Olifants watershed has varying terrain with approximately 24% of the area having slopes greater than 8%. The steep slopes (>30%) are located in the region of the escarpment.
3.2. Initial Model Run Analysis
An initial model simulation was executed for the calibration period 1988-2001 and the result presented in Figure 5. The time series analysis of the observed flow (Figure 5(a)) suggests significant seasonal flow during the wet months of January to April and October to December. The trend observed is expected because during this
Figure 4. Watershed discretized parameters. (a) Land use, (b) Soils, (c) Slopes and (d) Digital elevation model.
Table 3. Characteristics of the modeled Olifants Basin.
*Statistics based on threshold values of 10%, 10% and 10% for land use, soils and slope respectively.
time periods the Olifants Basin experiences rainfall which translates into the increase in stream flow. The model simulations captured the trend in the observed stream flow; however, it overestimated the observed stream flow time series by over 70%.
Figure 5. Comparison of simulated to observed monthly discharge (a) discharge hydrograph for 1988-2001 and (b) scatter plots for 1988-2001 at the 95% confidence level.
Although generally, the observed and simulated flow peaked in January, some high peaked predictions were observed in the months of February 1991, 1996 and 2000. An analysis into the correlation between the simulated and observed discharge revealed a coefficient of determination (R2) of 0.47 (Figure 5(b)) and an NS value of −8.97. Judging the initial model run by the efficiency measures of R2 and NS it was concluded that the model needed to be calibrated to achieve better parameter estimation required for a better model simulation. Prior to model calibration, relative parameter sensitivity analysis using SUFI-2 algorithm in identifying the most influential parameters on stream flow was carried out.
3.3. Parameter Sensitivity Analysis Using SUFI-2 Algorithm
The results of the relative sensitivity analysis of parameters using SUFI-2 is as shown in Table 4. From the initial fourteen parameters used in the sensitivity analysis, six were found to be sensitive to stream flow based on the t-stat and p-value (p < 0.05). Sensitivity of a parameter is determined by the t-stat and how significant that parameter is to the sensitivity analysis is measured by the p-value. Therefore a parameter with larger t-stat and smaller p-value exhibited greater sensitivity on the variable (stream flow) under consideration. Based on this, SCS runoff curve number (CN2) was ranked as the most sensitive parameter on stream flow. Since this parameter is a function of land use, soil permeability and antecedent soil conditions, a change in land use will commensurate into a relative change in stream flow. Other sensitive parameters with relative sensitivity value ranges of 0.00 to 0.02 were the base flow alpha factor for bank storage (ALPHA_BNK), soil evaporation compensation factor (ESCO), soil available water capacity (SOIL_AWC, mm H2O/mm soil), groundwater delay (GW_ DELAY, days) and groundwater “revap” coefficient (GW_REVAP).
Although the following parameters; threshold depth of water in the shallow aquifer required for return flow to occur (GWQMN, mm H2O), deep aquifer percolation fraction (RCHRG_DP), soil depth (SOL_Z, mm), soil conductivity (SOL_K, mm/h), effective hydraulic conductivity in the main channel (CH_K2, mm/h), base flow alpha factor (ALPHA_BF, days) were included in the sensitivity analysis, it was detected that they were statistically insignificant (p > 0.05) and hence a change in their input resulted in no significant effect on stream flow. Findings on parameter sensitivity to stream flow in this study is consistent with other studies around the globe [8] [40] [41] . However, in other jurisdictions parameters such as threshold depth of water in the shallow aquifer required for return flow to occur (GWQMN, mm H2O), deep aquifer percolation fraction (RCHRG_DP), soil depth (SOL_Z, mm), soil conductivity (SOL_K, mm/h), effective hydraulic conductivity in the main channel (CH_K2, mm/h), base flow alpha factor (ALPHA_BF, days) were detected to be sensitive to stream flow. The variations observed in parameter sensitivity to stream flow can best be explained by the differences inherent in the geomorphological characteristics of the area under investigation.
3.4. Base Flow Separation Prior to Calibration
In order to assess the accuracy of model simulations with regards to base flow index (BFI) estimation, an approach of base flow separation was carried out using observed stream flow data. This provided the basis for
Table 4. Sensitivity ranking of parameters for modeling stream flow in the Olifants Basin.
1―most sensitive; 6―less sensitive.
acceptance of the simulated base flow index (BFI). The separation of stream flow into base flow and direct runoff components (Figure 6) using the Web-based Hydrograph Analysis Tool (WHAT) indicated substantial amount (67%) of the stream flow to be contributed by direct runoff. BFI from observed stream flow was estimated to be 0.33 which implies a proportion of 33% of stream flow is contributed by base flow. A comparison of the simulated BFI and that obtained using base flow separation from observed data revealed no much significant difference with simulated BFI of 0.24. A breakdown of base flow on yearly basis revealed 66.9% of the total base flow for the calibration period (1988-2001) to have occurred within the period 1997-2001. The earlier years of the calibration period (1988-1996) recorded less base flow of 33.1%.
3.5. Calibration and Validation of Model
The initial ranges and final calibrated sensitive parameters to stream flow are presented in Table 5. A plot of monthly simulated to monthly observed stream flow (Figure 7 and Figure 8) indicated a good agreement between the datasets with an NSE of 0.88 and R2 of 0.89 for the calibration period (1988-2001) and NSE of 0.67 and R2 of 0.78 for the validation period (2002-2013). The model captured well the monthly time series of stream flow as well as the trend during both calibration and validation periods.
Although, observed and simulated discharge matched well for calibration and validation periods there was an average magnitude overestimation of the observed discharge with PBIAS of −11.49% for the calibration period and −20.69% for the validation period. The observed and simulated mean annual flow (MAF) during the calibration period (1988-2001) was 1175 Mm3/a (37.27 m3/s) and 1310 Mm3/a (41.55 m3/s) respectively which represent an overestimation of the observed stream flow by 11.48%. For the validation period (2002-2013) the observed and simulated MAF were 1193 Mm3/a (37.82 m3/s) and 1440 Mm3/a (45.65 m3/s) respectively also indicating an overestimation of the observed by 20.69%. The cumulative simulated MAF of 2750 Mm3/a achieved in this study compares differently from the 2040 Mm3/a and 1992 Mm3/a recorded by the WSAM [24] and WR90 [42] studies respectively for the Basin. The difference may be attributed to the spatio-temporal change in rainfall occurring throughout the years. Considering the model performance statistics (Table 6) for both calibration and validation periods and on the criteria set out by Moriasi et al. [39] for assessing model performance, the set up model was rated “good” for the Olifants Basin. These measures of model performance indicate that the model captures well the observed stream flow.
However, a comparison of the measures of statistics for the calibration and validation period (Table 6) reveals a better performance of the model during the calibration period as compared to the validation period. This observation agrees with the studies of Moriasi et al. [39] in which model performance during the calibration period did well compared to the validation period.
4. Conclusions and Recommendation
Demonstrated in this study is the calibration, validation and uncertainty analysis for the Olifants Basin. The calibrated SWAT model indicated statistical reliability in simulating the stream flow of the Olifants Basin. However a comparison of the model during calibration and validation revealed a better simulation at the calibration stage than at the validation stage. This is to suggest that if data are available for other variables (i.e. sediment,
Figure 6. Monthly base flow separation for the calibration period 1988-2001.
Figure 7. Monthly discharge calibration for the period 1988-2001, (a) hydrograph analysis and (b) scatter plot at the 95% confidence level.
Figure 8. Monthly discharge validation for the period 2002-2013, (a) hydrograph analysis and (b) scatter plot at the 95% confidence level.
Table 5. Model calibrated parameter values.
*Average estimated for the basin.
Table 6. Monthly time step calibration and validation performance statistics.
water quality, etc.) the model can equally be calibrated to simulate those variables with good measures of statistics. With available and reliable data, the SWAT tool comes in handy as a decision support tool that can influence policy directions on watershed management processes and more especially on water resources.
Acknowledgements
Tshwane University of Technology is acknowledged for the financial support for the study. The authors express their gratitude to the Department of Water Affairs and the South African Weather Service for freely providing the data used for the study.
Cite this paper
Charles Gyamfi,Julius Musyoka Ndambuki,Ramadhan Wanjala Salim, (2016) Application of SWAT Model to the Olifants Basin: Calibration, Validation and Uncertainty Analysis. Journal of Water Resource and Protection,08,397-410. doi: 10.4236/jwarp.2016.83033
References
- 1. Betrie, G.D., Mohamed, Y.A., van Griensven, A. and Srinivasan, R. (2011) Sediment Management Modeling in the Blue Nile Basin Using SWAT Model. Hydrology and Earth System Sciences, 15, 807-818.
http://dx.doi.org/10.5194/hess-15-807-2011 - 2. Panhalkar, S.S. (2014) Hydrological Modeling Using SWAT Model and Geoinformatic Techniques. The Egyptian Journal of Remote Sensing and Space Sciences.
- 3. Singh, V., Bankar, N., Salunkhe, S.S., Bera, A.K. and Sharma, J.R. (2013) Hydrological Stream Flow Modeling on Tungabhadra Catchment: Parameterization and Uncertainty Analysis Using SWAT CUP. Current Science, 104, 1187-1199.
- 4. Adeogun, A.G., Sule, B.F. and Salami, A.W. (2015) Simulation of Sediment Yield at the Upstream Watershed of Jebba Lake in Nigeria Using SWAT Model. Malaysian Journal of Civil Engineering, 27, 25-40.
- 5. DWAF (2005) Olifant River Water Resources Development (ORWRP) Environmental Impact Assessment (12/12/20/ 553). Infrastucture Development.
- 6. Obuobie, E. and Bernd, D. (2008) Using SWAT to Evaluate Climate Change Impact on Water Resources in the White Volta River Basin. West Africa Conference on International Research on Food Security, Natural Resource Management and Rural Development, University of Hohenheim, Tropentag, 7-9 October 2008.
- 7. Merrey, D.J., Drechsel, P., Penning de Vries, F.W.T. and Sally, H. (2005) Integrating “Livelihoods” into Integrated Water Resources Management: Taking the Integration Paradigm to Its Logical Next Step for Developing Countries. Regional Environmental Change, 5, 197-204.
http://dx.doi.org/10.1007/s10113-004-0088-5 - 8. Setegn, S.G., Srinivasan, R. and Dargahi, B. (2008) Hydrological Modeling in the Lake Tana Basin, Ethiopia Using SWAT Model. The Open Hydrology Journal, 2, 49-62.
http://dx.doi.org/10.2174/1874378100802010049 - 9. Chou, S., Russ, B. and Anne, W. (1997) Water Scarcity in River Basins as a Security Problem. Woodrow Wilson International Centre for Scholars, Environmental change and Security Project, Washington DC, 96-105.
- 10. Xie, M. (2006) Integrated Water Resources Management (IWRM)—Introduction to Principles and Practices. World Bank Institute.
- 11. Carius, A., Dabelko, D.G. and Wolf, A.T. (2004) Water, Conflict and Cooperation, Policy Briefing Paper for United Nations and Global Security Initiative.
- 12. UNDP (2006) Summary Human Development Report. Beyond Scarcity: Power, Poverty and the Global Water Crisis.
- 13. Biswas, A.K. (2001) Management of International Waters: Opportunities and Constraints, in Sustainable Development of the Ganges-Brahmaputra-Meghna Basins. In: Biswas, A.K. and Uitto, J.I., Eds., United Nations University Press, Tokyo, 1-16.
- 14. Gleick, P.H. (2000) The Changing Water Paradigm: A Look at Twenty-First Century Water Resources Development. Water International, 25, 127-138.
http://dx.doi.org/10.1080/02508060008686804 - 15. Ullrich, A. and Volk, M. (2009) Application of the Soil and Water Assessment Tool (SWAT) to Predict the Impact of Alternative Management Practices on Water Quality and Quantity. Agricultural Water Management, 96, 1207-1217.
http://dx.doi.org/10.1016/j.agwat.2009.03.010 - 16. Schuol, J., Abbaspour, K.C., Srinivasan, R. and Yang, H. (2008) Estimation of Freshwater Availability in the West African Sub-Continent Using the SWAT Hydrologic Model. Journal of Hydrology, 352, 30-49.
http://dx.doi.org/10.1016/j.jhydrol.2007.12.025 - 17. Yang, J., Reichert, P. and Abbaspour, K.C. (2007) Bayesian Uncertainty Analysis in the Distributed Hydrologic Modeling: A Case Study in the Thur River Basin (Switzerland). Water Resources Research, 43, W10401.
http://dx.doi.org/10.1029/2006WR005497 - 18. Simic, Z., Milivojevic, N., Prodanovic, D., Milivojevic, V. and Perovic, N. (2009) SWAT-Based Runoff Modeling in Complex Catchment Areas—Theoretical Background and Numerical Procedures. Journal of the Serbian Society for Computational Mechanics, 3, 38-63.
- 19. Neitsch, S.L., Arnold, J.G., Kiniry, J.R. and Williams. J.R (2005) Soil and Water Assessment Tool Theoretical Documentation. Version 2005.
- 20. Arnold, J.G. and Fohrer, N. (2005) SWAT2000: Current Capabilities and Research Opportunities in Applied Watershed Modeling. Hydrological Processes, 19, 563-572.
http://dx.doi.org/10.1002/hyp.5611 - 21. Obuobie, E. and Diekkrüger, B. (2008) Using SWAT to Evaluate Climate Change Impact on Water Resources in the Olifant River Basin, West Africa. Conference on International Research on Food Security, Natural Resource Management and Rural Development, University of Hohenheim, Stuttgart, 7-9 October 2008.
- 22. Li, Z., Liu, W., Zhang, X. and Zheng, F. (2009) Impacts of Land Use Change and Climate Variability on Hydrology in an Agricultural Catchment on the Loess Plateau of China. Journal of Hydrology, 377, 35-42.
http://dx.doi.org/10.1016/j.jhydrol.2009.08.007 - 23. Neitsch, S.L., Arnold, J.G., Kiniry, J.R., Williams, J.R. and King, K.W. (2011) Soil and Water Assessment Tool Theoretical Documentation Version 2009. Grassland, Soil and Research Service, Temple.
- 24. Schultz, C.B. and Watson, M.D. (2002) WSAM: Water Situation Assessment Model Version 3: A Decision Support System for Reconnaissance Level Planning. Volume 1: Theoretical Guide. ARCUS-GIBB and DWAF, Republic of South Africa.
- 25. IWMI (2008) Baseline Report Olifants River Basin in South Africa: A Contribution to the Challenge Program Project 17 “Integrated Water Resource Management for Improved Rural Livelihoods: Managing Risk, Mitigating Drought and Improving Water Productivity in the Water Scarce Limpopo Basin”.
- 26. Schulze, R.E., Maharaj, M., Lynch, S.D., Howe, B.J. and Melvil-thomson, B. (1997) South African Atlas for Agrohydrology and Climatology. University of Natal, Pietermaritzburg.
- 27. FAO (2002) Major Soils of the World. Land and Water Digital Media Series. Food and Agricultural Organization of the United Nations. FAO, Rome.
- 28. FAO (2005) Digital Soil Map of the World and Derived Soil Properties of the World. Food and Agricultural Organization of the United Nations. FAO, Rome.
- 29. Batjes, N.H. (2002) ISRIC-WISE Global Data Set of Derived Soil Properties on a 0.5 by 0.5 Degree Grid (Version 2.0). Report 2002/03. International Soil Reference and Information Centre (ISRIC), Wageningen.
- 30. Anderson, J.R., Hardy, E.E., Roach, J.T. and Witmer, W.E. (1976) A Land Use and Land Cover Classification System for Use with Remote Sensing Data. USGS Professional Paper 964, 138-145.
- 31. Neitsch, S.L., Arnold, J.G., Kiniry, J.R., Srinivasan, R. and William, J.R. (2002) Soil and Water Assessment Tool User’s Manual. Version 2000.
- 32. FAO (2003) The Digital Soil Map of the World. Version 3.6.
- 33. Abbaspour, K.C. (2012) SWAT-CUP-2012.SWAT Calibration and Uncertainty program—A User Manual. Swiss Federal Institute of Aquatic Science and Technology, Dübendorf.
- 34. Faramarzi, M., Abbaspour, K.C., Schulin, R. and Yang, H. (2009) Modelling Blue and Green Water Resources Availability in Iran. Hydrological Processes, 23, 486-501.
http://dx.doi.org/10.1002/hyp.7160 - 35. Schuol, J., Abbaspour, K.C., Yang, H., Srinivasan, R. and Zehnder, A.J.B. (2008) Modeling Blue and Green Water Availability in Africa. Water Resources Research, 44, W07406.
http://dx.doi.org/10.1029/2007wr006609 - 36. Abbaspour, K.C., Yang, J., Maximov, I., Siber, R., Bogner, K., Mieleitner, J., Zobrist, J. and Srinivasan, R. (2007) Modelling Hydrology and Water Quality in the Pre-Alpine/Alpine Thur Watershed Using SWAT. Journal of Hydrology, 333, 413-430.
http://dx.doi.org/10.1016/j.jhydrol.2006.09.014 - 37. Abbaspour, K.C., Johnson, C.A. and van Genuchten, M.T. (2004) Estimating Uncertain Flow and Transport Parameters Using a Sequential Uncertainty Fitting Procedure. Vadose Zone Journal, 3, 1340-1352.
http://dx.doi.org/10.2136/vzj2004.1340 - 38. Coffey, A.E., Workman, S.R., Taraba, J.L. and Fogle, A.W. (2004) Statistical Procedures for Evaluating Daily and Monthly Hydrologic Model Predictions. Transaction of the American Society of Agriculture Engineers, 47, 59-68.
http://dx.doi.org/10.13031/2013.15870 - 39. Moriasi, D.N., Arnold, J.G., van Liew, M.W., Bingner, R.L., Harmel, R.D. and Veith, T.L. (2007) Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Transactions of the ASABE, 50, 885-900.
http://dx.doi.org/10.13031/2013.23153 - 40. Vaghefi, S.A., Mousavi, S.J., Abbaspour, K.C., Srinivasan, R. and Yang, H. (2013) Analyses of the Impact of Climate Change on Water Resources Components, Drought and Wheat Yield in a Semi-Arid Regions: Karkheh River Basin in Iran. Hydrological Processes, 28, 2018-2032.
http://dx.doi.org/10.1002/hyp.9747 - 41. Yang, H., Reichert, P., Abbaspour, K.C., Xia, J. and Yang, H. (2008) Comparing Uncertainty Analysis Techniques for SWAT Application to the Chaohe Basin in China. Journal of Hydrology, 358, 1-23.
http://dx.doi.org/10.1016/j.jhydrol.2008.05.012 - 42. Midgley, D.C., Pitman, W.V. and Middleton, B.J. (1994) Surface Water Resources of South Africa, Volumes I, II, III, IV, V and VI. Reports No’s. 298/1.1/94, 298/2.1/94, 298/3.1/94, 298/4.1/94, 298/5.1/94 and 298/6.1/94, Water Research Commission, Pretoria.
NOTES
*Corresponding author.