Journal of Water Resource and Protection
Vol.06 No.15(2014), Article ID:51827,25 pages
10.4236/jwarp.2014.615136
Kp pan evaporation and ETo monthly maps using information of 60 weather observatories included in the Climate Normals (1941-1970) from Mexico
Martín Mundo-Molina
Investigation Centre, Faculty of Engineer, Autonomous University of Chiapas, Tuxtla Gutiérrez, Mexico
Email: ic_ingenieros@yahoo.com.mx
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 21 September 2014; revised 18 October 2014; accepted 6 November 2014
ABSTRACT
The most precise equation in order to estimate the evapotranspiration (ET) of crops is the Penman- Monteith (PM). However, the PM equation needs specific data that, in the majority of Mexico’s irrigation districts, it is not available because there are few automated weather stations. For this reason, it is convenient to develop simple methods that allow to precise estimation of ET. A reliable way to estimate ET is by using the pan evaporation that, according to the revised literature, continues to be used nowadays. Investigators like to include its use in irrigation water management projects in various parts of the world. However, this method uses Kp from the FAO that is not calibrated in Mexico. The use of FAO Kp affects the precision of the results, since some variables like radiation, wind, temperature and relative humidity vary from place to place; therefore ET is under estimated or overestimated. This paper presents an original contribution across method to estimate “Kp pan evaporation and ETo monthly maps”, using information from 60 weather observatories included in The Climate Normals (1941-1970) from Mexico, based on the PM method and the class A pan evaporation. Once the Kp values were obtained from each weather observatory, the Kringing method was used. This way, by interpolating data of the triad “latitude, longitude and Kp” and “latitude, longitude and ET”, monthly normalized maps of Kp and ET were established for Mexico, except the upland areas (Sierra Madre Occidental and Sierra Madre Oriental), as well as other highland zones above 2700 meters over sea level, for the highest observatory is located in Toluca, State of Mexico (key 14-0039), at 2680 m over sea level.
Keywords:
reference evapotranspiration, pan evaporation, Kp pan evaporation

1. Introduction
Earth’s climate instability, local climate changes and the potential threat of anthropogenic climate change (one of the most discussed hypothesis nowadays), is generating abundant rainfalls and great runoffs in certain zones of the country (especially when extreme hydrometeorology events occur), and droughts in others locations. The anthropogenic climate change hypothesis presents unfavorable scenarios for the immediate future, especially for the northern part of Mexico where water is scarce. Mexico’s most important irrigation districts are located in the north, and it’s in the agricultural sector where most water is consumed, as irrigation districts use 80 of every 100 liters of water in the country with a very low efficiency (50% of water is wasted). It is precisely in this sector where water must be used effectively, by programming and properly estimating the water demand of crops.
One of the most important components of the hydrologic cycle is the evapotranspiration (ET), the estimation of which is essential in the fields of hydrology and irrigation engineering. In hydrology, the ET is needed for planning management of water resources in watersheds, and for the design of major engineering works. In irrigation engineering, the crop reference evapotranspiration is fundamental for the devising and water administration in irrigation systems. This depends on an adequate estimation of crop water requirements [1] -[3] , where ET plays an essential part. Date and frequency of irrigation also depend on the accuracy of the ET estimations, as well as equitable distribution of water in irrigation zones [4] . This planning is important in Mexico where irrigation strategies need to maximize production per unit of water used. It is crucial that farmers improve not only irrigation methods, but also the knowledge of when and how much to water crops.
2. Background
To calculate irrigation schedules it is necessary to estimate ET through some method. There are methods like the Penman-Monteith, the Hargreaves, the Radiation and the FAO 24 to estimate with certain precision such variable, yet if more accuracy is required direct measurement devices can be used, such as the energy balance method (Bowen relation), the eddy covariance method, the lysimeter method and the automated weather stations. In contrast, another and much simpler method to estimate ET is the class A pan evaporation (PE); this method is frequently used in Israel and Spain’s irrigation districts [5] .
Mexico is introducing automated weather stations, especially in the northern part of the country; however, few users have access to the technology or the economic resources to acquire this type of stations. For this reason, developing simple and economic alternatives that allow the calculus of the ET value with an adequate precision is mandatory, either for administrating water resources and designing hydraulic projects or, in the case of irrigation engineering, for the correct determination of the irrigation frequency schedule. The Penman-Mon- teith is one of the most reliable methods but it needs data that either is not available for the user or inexistent. A version of the PM equation [6] is the following:
 (1)
(1)
where:
ETo = Referenced crop evapotranspiration (mm・h−1)
Rn = Net radiation on crop’s surface (MJ・m−2・h−1)
G = Sensible heat flux from soil (MJ・m−2・h−1)
Cn = Numerator constant with changes reference type and calculation time step (Cn = 900, daily)
Cd = Denominator constant with changes reference type and calculation time step (Cd = 0.34, daily)
T2 = Hourly average air temperature at 2 m over the ground (˚C)
U2 = Hourly wind velocity at 2 m over ground (ms−1)
The values es and ea are calculated using the maximum and minimum temperature per hour. G value is estimated during the day with the following expression [6] :
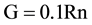 (2)
(2)
And during the night with:
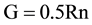 (3)
(3)
These equations were validated using grass as the referenced crop, with a height of 0.12 m and a surface resistance of rc = 70 sm−1 y α = 0.23 (albedo).
On the other hand a simple way to calculate ET is by the use of the evapotranspiration equation that relates ET with Ev through a pan evaporation coefficient (Kp). According to [7] - [11] , the PE is widely used in water management projects on many latitudes of the world, sometimes even with more assiduity than other, more precise methods; for example, in Israel, its use in agricultural holdings with drip irrigation is very common [5] . The PE is considered an adequate method to use at an ample range of locations, included humid zones [12] . This method estimates crop evapotranspiration using grass as reference. Grass evapotranspiration differs from the evaporation of the pan evaporation, depending on the characteristics of the site and climate conditions. Both relate through the Kp pan evaporation as it follows [7] :
 (4)
(4)
where:
ETo = evapotranspiration of the reference crop (mm)
Ev = evaporation of the class-A pan evaporimeter (mm)
According to [13] many field studies have been made to compare the PE against empiric methods. Several of these studies were revised by [14] and almost all of the reported estimations based on the PE method were consistent and close to the precision level obtained from methods catalogued as the best [13] . [15] compared the Penman-Monteith method with the FAO 24 method, including the PE, in 16 districts of Australia for a wide range of climatic conditions. His principal conclusions on the PE method were the next: a) a satisfactory correlation exists between the PE and the Penman-Monteith methods for the total evaporation of three days or more. However, the pan evaporation data is obsolete unless precise values of Kp are used, b) the Kp of PE depends on local conditions so it must be determined using the pan evaporation data and the ET data obtained by the Penman-Monteith equation or the radiation method. With this basic idea a methodology was developed to calculate normalized monthly Kp pan evaporation and monthly isocurves from PE and the Penman-Monteith equation [6] . With the final aim to minimize errors and estimate the Kp pan evaporation from PE in its range of values (between 0 and 1), the coefficients proposed by [16] were used as reference values and also the characteristics of its evaporimeter. On the other hand, pan evaporation depends on the exact placement of the pan relative to wind exposure. Pans surrounded by tall grass may evaporate 20 to 30 percent less than pans placed in a fallow area. Rainfall may occur during the irrigation season and may add water to the pan, or thirsty animals wandering in the area may drink from the pan, thus detracting from its usefulness. To avoid water loss to drinking animals (especially birds), pans are often covered by screens. This may reduce the evaporation rate by some 10 to 20 percent, thus requiring the use of a correction factor. The differences between Kp from arid zones and Kp from humid zones were also considered. The authors recommended reducing the values from Table 1, 20% less in desert or semi desert zones, especially in places with intense wind and 5% to 10% for places with moderate wind (for humid and cold zones the Kp value was not reduced). For dry places the Kp value was elevated between a 20% and 30%. For humid zones with moderate wind, Kp was elevated between a 5% and a 10%.
Kp pan evaporation and ET monthly estimation in Mexico
Sixty weather observatories were located and analyzed through the country. This information was obtained from The Climate Normals (1941-1970), elaborated by the now extinct Department of Agriculture and Hydraulic Resources [17] that contains normalized climate normals data from 1941 to 1970. These observatories have climate information that works for the Penman-Monteith method [13] , which was used to calculate ETo in each climate observatory (equation (1)). The observatories used for the ETo calculus were the following:
On the other hand, the monthly evaporation (Ev) values in each observatory were obtained (see Table 2), which were measured in the field over a 30 year period. Thus, when clearing ET from the equation (4), we have:
 (5)
(5)
Matched 1 and 5:
 (6)
(6)
Table 1. Kp coefficients proposed by FAO [16] .
where Fs is equal to equation (1). Thus, the standard monthly Kp values were estimated for each observatory with equation 6, as shown in Table 2. Results are presented in Table 3.
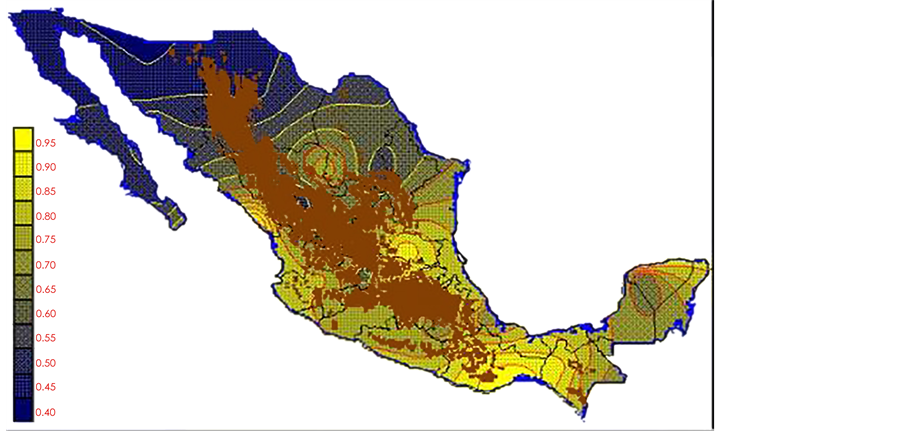
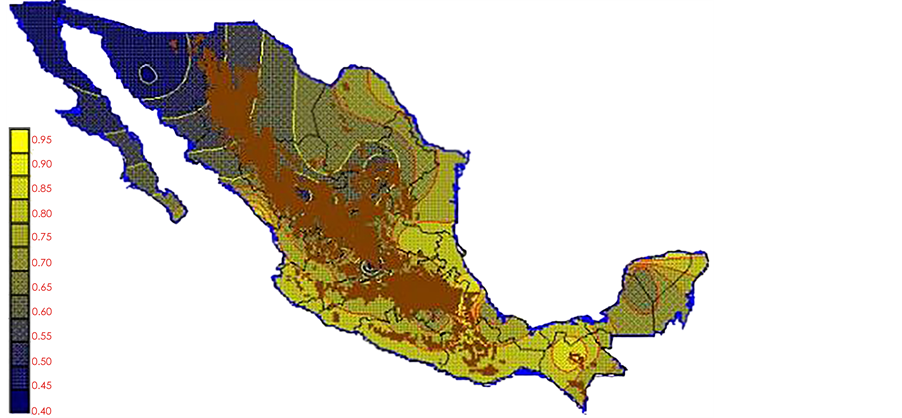
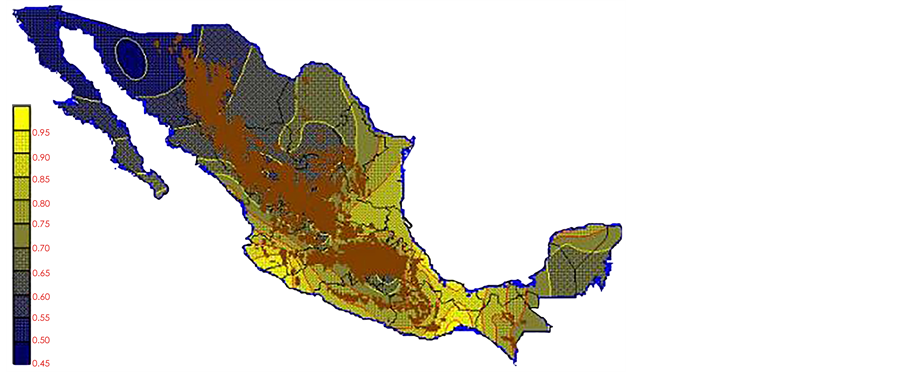
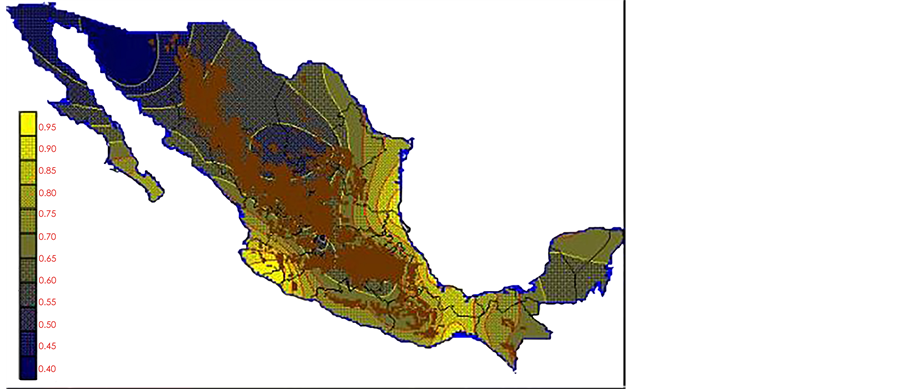
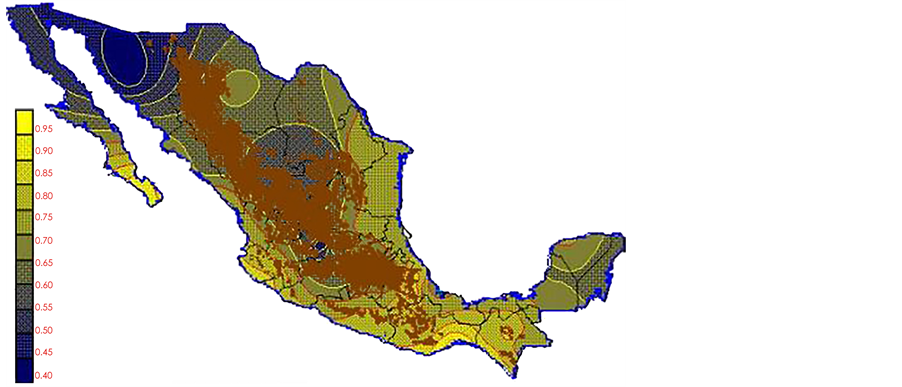
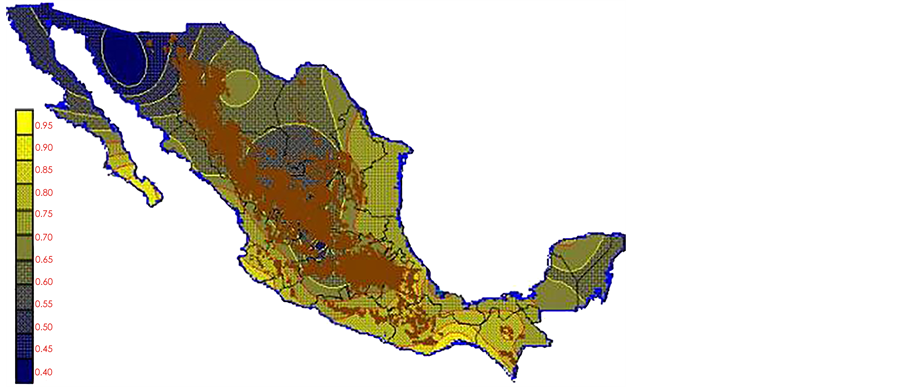
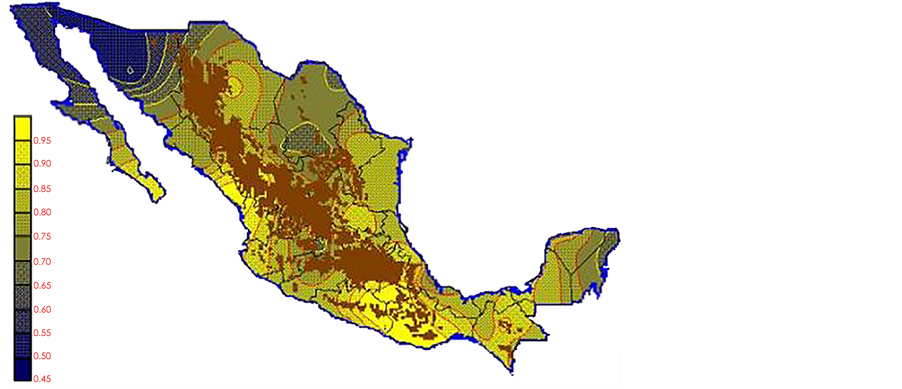
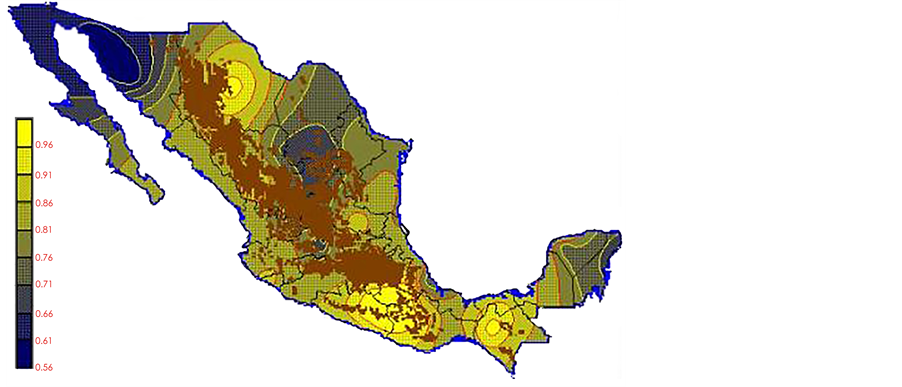
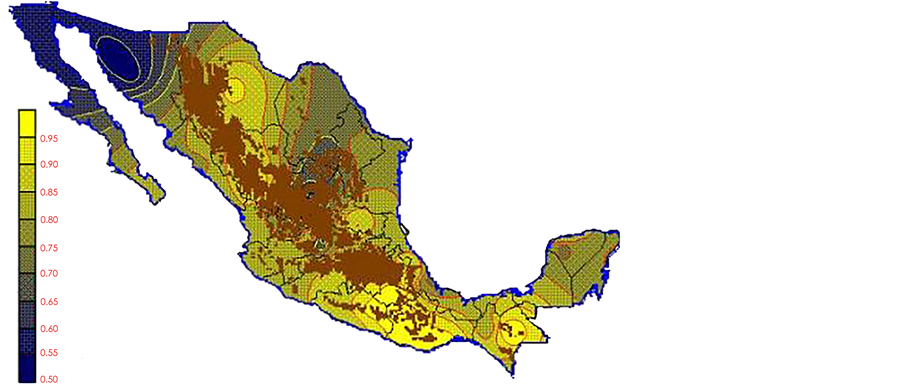
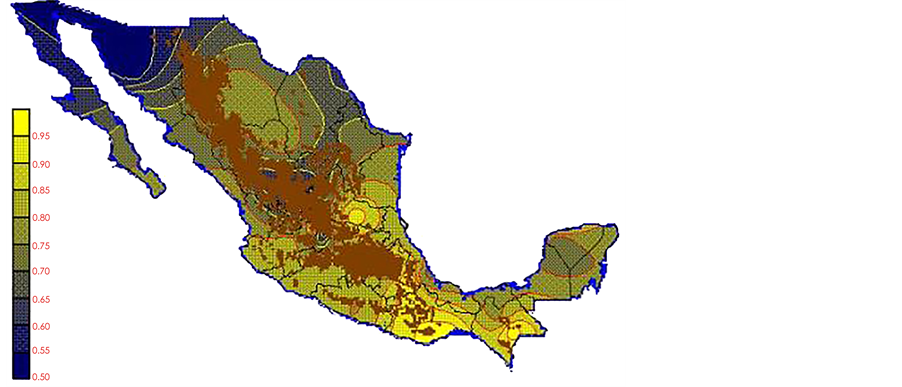
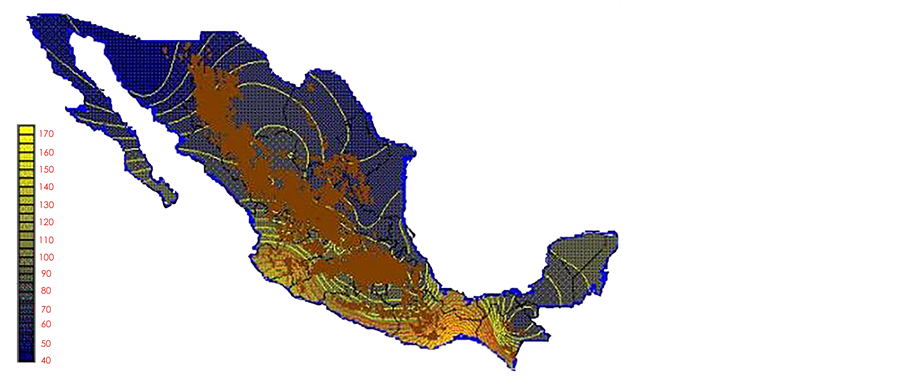
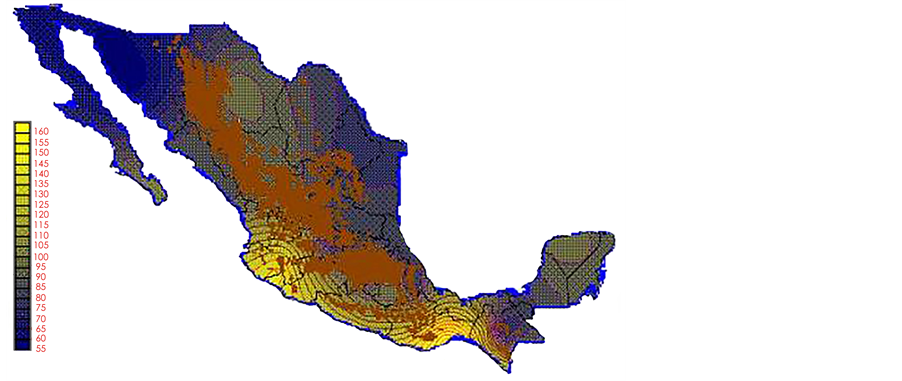
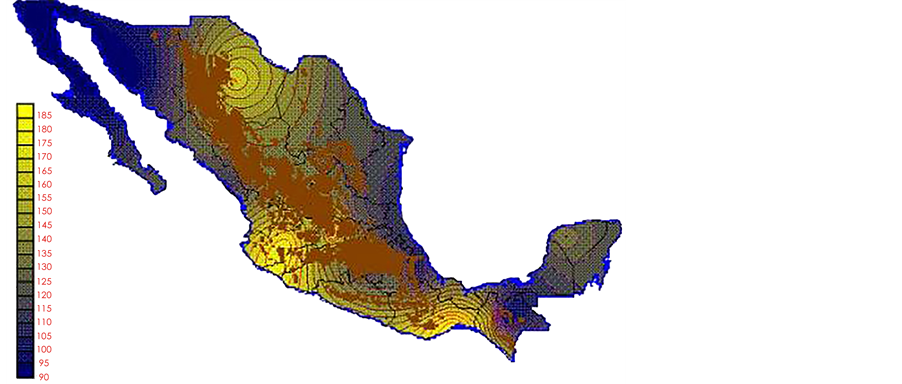
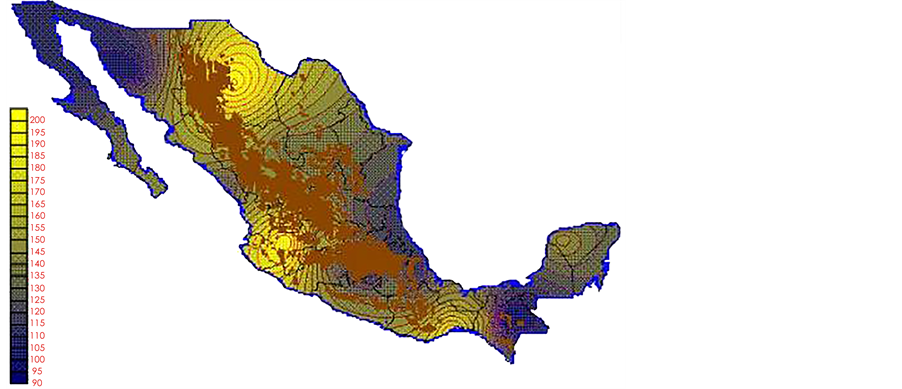
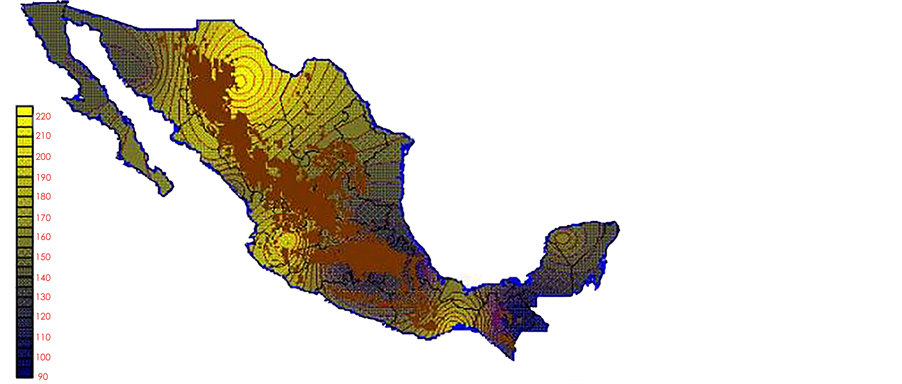
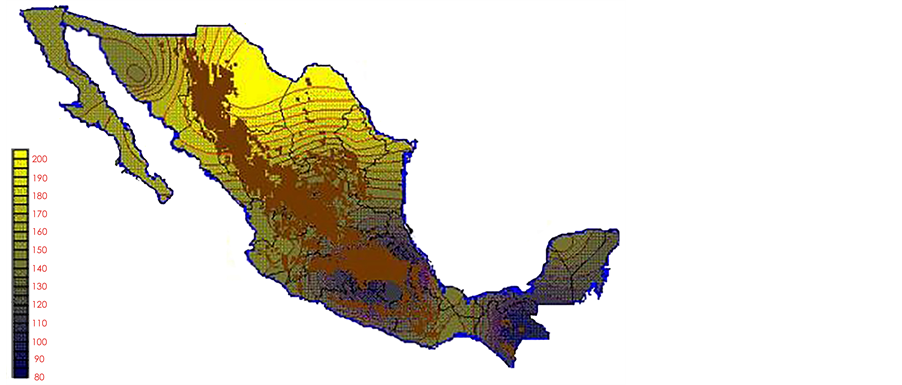
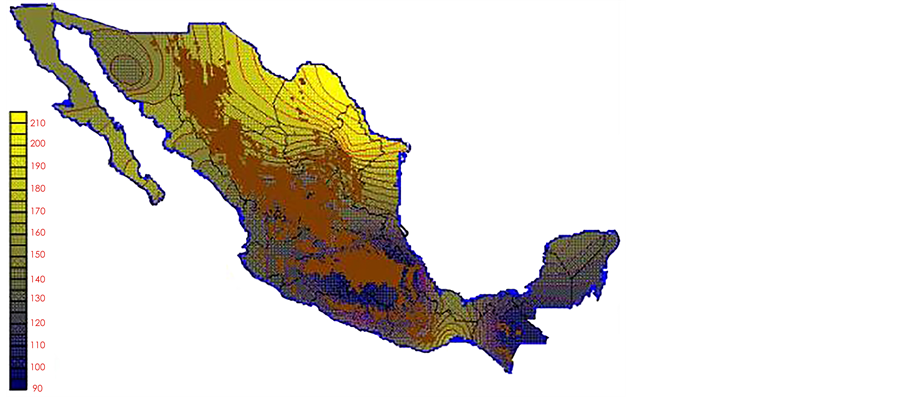
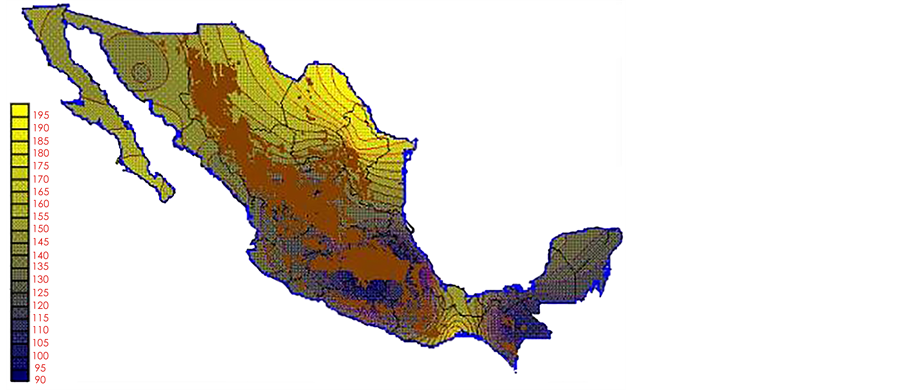
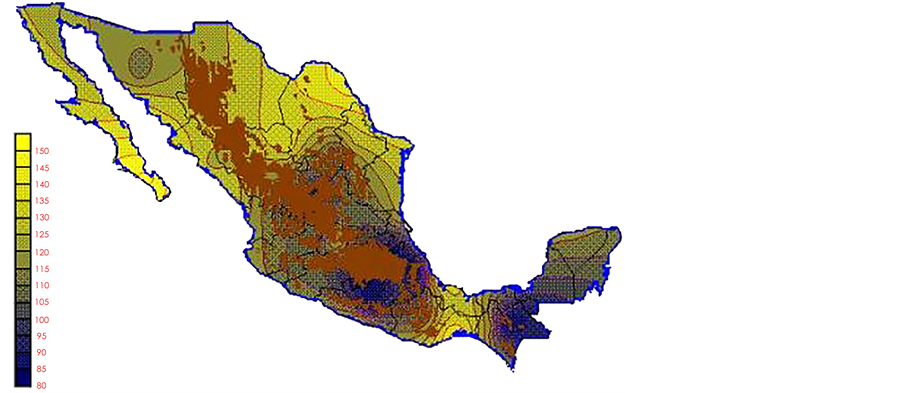
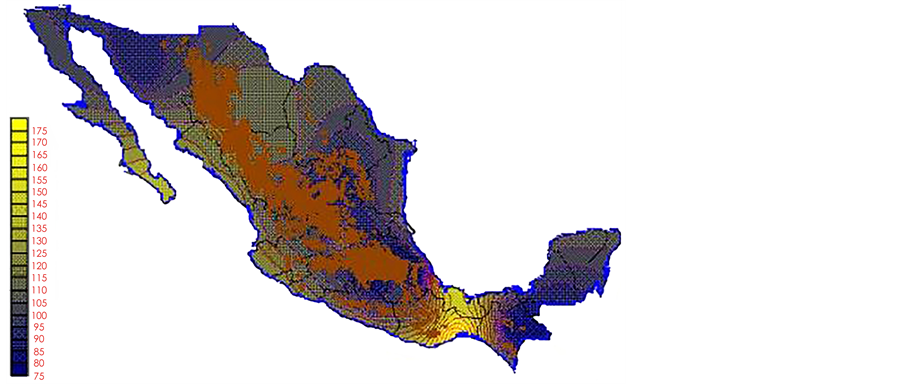
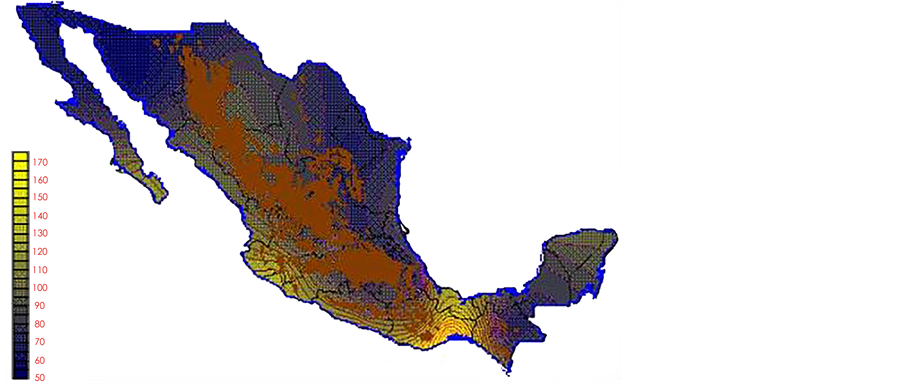
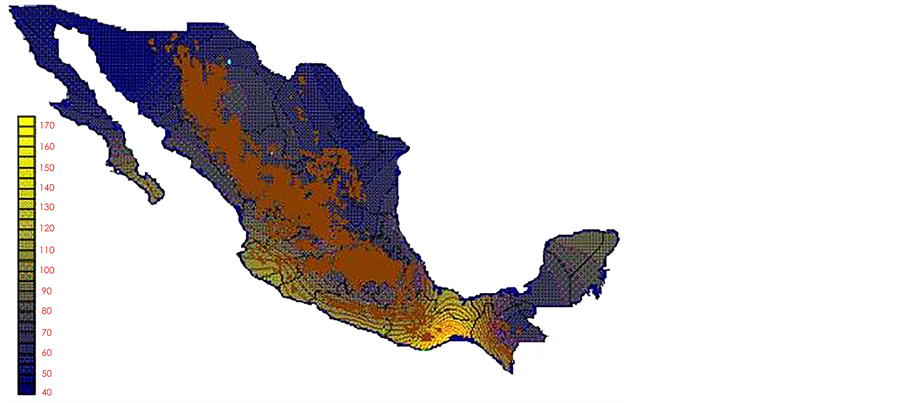
With the values from Table 3, isocurves and maps of Kp pan evaporation and ETo were elaborated and standardized for all the country, by interpolating the latitude, longitude, Kp and ET data respectively (as a triad of values) with a Kringing grid method. With this data, a rectangular calculation mesh (rows and columns) was established. The grid method produces a regulated arrangement of the Z (Kp or ET) values from the XYZ (latitude, longitude and Kp or ET) irregularly spaced. The terms “irregularly spaced” mean that the points do not follow a particular pattern over a map, e.g. in practice many “spaces” were left without any data, which the method (Kringing) estimates by taking as a reference the closest values, filling these spaces by interpolation. The Kringing method has a mean weighed interpolation algorithm and incorporates a linear variogram model. The variogram is used to determine the local vicinity of the observations when an interpolation is performed in each node of the grid. The illustrations Figures 1-12 show the Kp estimations for each month, normalized for Mexico.
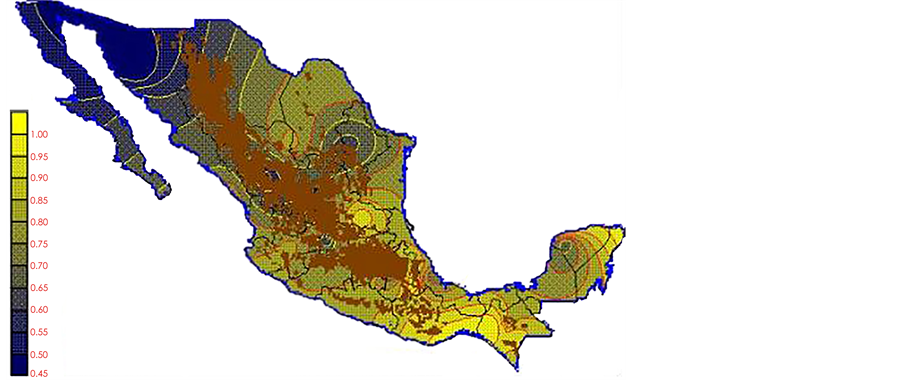
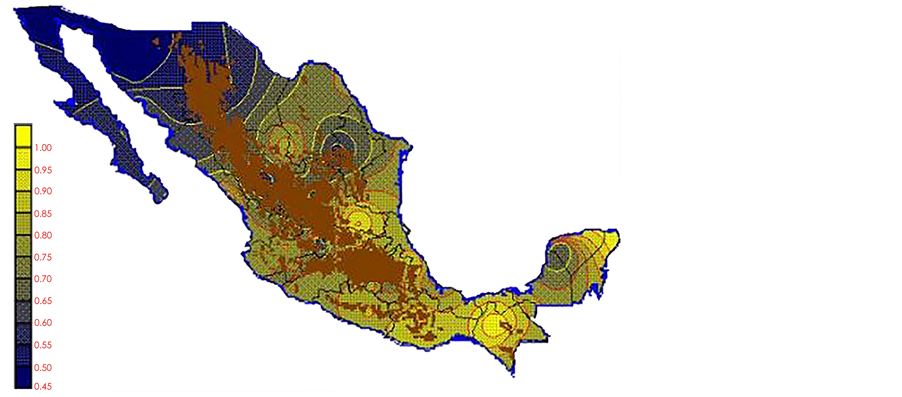
With clearing Fs from equation 6 and the Kp and ETo data from Table 2 and Table 3 respectively, the ETo monthly normalized data was obtained in all observatories of the country (see Table 4). Thus, when latitude, longitude and ET data was interpolated, the maps shown in illustrations Figures 13-24 were completed.
3. Discussion
With the proposed methodology in this paper, new monthly values for Kp pan evaporation were estimated for the 1941-1970 period of the climatological normals of the Mexican republic. The monthly Kp pan evaporation values have a national coverage. The use of Kp maps or the isolines make the PE not only a simple method but also an applicable one to any latitude of the country. However, it is important to take in consideration that: a) in places above 2700 m over sea level there are no climatological stations (Sierra Madre occidental, sierra Madre del Sur and mountains 2700 meters over sea level, which are represented on the maps with a brown color), and the Kp evaporation pan and ETo results may or may not be precise; therefore they must be used with caution,
Table 2. Climatic data.
Figure 1. January Kp.
Figure 2. February Kp.
Table 3. Kp coefficients for each observatory in the country.
Figure 3. March Kp.
Figure 4. April Kp.
Figure 5. May Kp.
Figure 6. June Kp.
Figure 7. July Kp.
Figure 8. August Kp.
Figure 9. September Kp.
Figure 10. October Kp.
Figure 11. November Kp.
Figure 12. December Kp.
Figure 13. ETo January.
Figure 14. ETo February.
Figure 15. ETo March.
Figure 16. ETo April.
Figure 17. ETo May.
Figure 18. ETo June.
Figure 19. ETo July.
Figure 20. ETo August.
Figure 21. ETo September.
Figure 22. ETo October.
Figure 23. ETo November.
Figure 24. ETo December.
b)The method only uses an average monthly data from 30 years climate normal to estimate ETo values because the monthly data were not available for each year, c)The method uses only 60 weather observatories located mainly in urban areas because in Mexico there are only 60 weather observatories, d) The interpolation method used data of weather observatories located from 3 meters over sea levels (Mazatlán Sinaloa) up 2680 meters over sea level (Toluca, Mexico), e) is important to note that if paper were results used to estimate Kp data for a given Ev, bread surrounding characteristics should be considered as indicated in the last paragraph of index 2.
On the other hand numerous studies suggest that measures must be taken when interpreting the results found with the PE method, because the location, the maintenance of the pan evaporimeter and the Kp estimation influence in the precision of the ET. For example, the size of the evaporimeter has important effects on the Kp factor in dry zones, when these are surrounded by dry and barren surfaces. In humid climates the size of the evaporimeter is less significant, however when it is placed in large crop areas, e.g. in grass crops, its size or may not be of importance [8] . Other aspect to have in consideration is the low values of Kp in dry and windy climates, compared to the ones obtained from humid places. Some of this assertions have been reported by [18] and [16] . In 1996 [19] published a study which explained that in dry climate, the Kp estimations could be altered under the following conditions: severe drought, strong winds and low radiation situations in some spring and autumn months; under these circumstances the Kp pan evaporation values can be reduced down to half of the normal value when placed in large grass areas. More recently, [20] reported that the Kp values for wheat decreased between a 20% and a 25% in dry and windy days in April. The normal value ranges oscillate between 0.90 and 0.95 for wheat crops (high stature crops). Apparently high stature crops cause certain aerodynamic conditions in pan evaporimeters that, in arid zones, affect less said factors. For dry and windy climates it is necessary to calibrate this methodology, as well as possessing data from several years to emit judgment on the obtained Kp pan evaporation values.
4. Conclusion
Estimating ET to determine calendars or water demand remains a main problem in the irrigation districts, even when there are a variety of direct and indirect methods. For example, an indirect and precise method like the Penman-Monteith needs data that in most cases are either not available for the user, or inexistent. The ET calculus through automated weather stations is a direct and precise method, but its elevated cost makes it difficult to use. Automated weather stations have a good precision to measure climatological parameters and calculate ET, though the cost is extremely high as well. There is a simple method to estimate ET using the class A pan evaporimeter (PE), which can perform ET estimations in a simple and economic way (the cost of the PE is 500 American dollars approximately), but if the right Kp pan evaporation values are not used, the accuracy of these estimations will not be satisfactory. This paper presents a method to estimate “Kp pan evaporation and ETo
Table 4. ET monthly estimation from all observervatories in the country.
monthly maps”, using information from 60 weather observatories included in The Climate Normals (1941-1970) from Mexico, based on the PM method and the class A pan evaporation. Once the Kp values were obtained from each weather observatory, the Kringing method was used. This way, by interpolating data of the triad “latitude, longitude and Kp” and “latitude, longitude and ET”, monthly normalized maps of Kp and ET were established for Mexico, except the upland areas (Sierra Madre Occidental and Sierra Madre Oriental), as well as other highland zones above 2700 meters over sea level, for the highest observatory is located in Toluca, State of Mexico (key 14-0039), at 2680 m over sea level. For their relevance in this paper is presented 12 ETo maps and 12 Kp maps.
References
- Michalopoulou, H. and Papaioannou, G. (1991) Reference Crop Evapotranspiration over Greece. Agricultural Water Management, 20, 209-221. http://dx.doi.org/10.1016/0378-3774(91)90018-E
- Hashmi, M.A. and García, L.A. (1998) Spatial and Temporal Errors in Estimating Regional Evapotranspiration. Journal of Irrigation and Drainage Engineering, 124, 108-114. http://dx.doi.org/10.1061/(ASCE)0733-9437(1998)124:2(108)
- Al-Ghobari, H.M. (2000) Estimation of Reference Evapotranspiration for Southern Region of Saudi Arabia. Irrigation Science, 19, 81-86. http://dx.doi.org/10.1007/s002710050004
- Omary, M. and Izuno, F.T. (1995) Evaluation of Sugarcane Evapotranspiration from Water Table Data in Everglades Agricultural Area. Agricultural Water Management, 27, 309-319. http://dx.doi.org/10.1016/0378-3774(95)01149-D
- Fereres, E. (2000) Personal Communication.
- Allen, R.G., Walter, I.A., Elliot, R., Mecham, B., Jensen, M.E., Itenfisu, D., Howell, T.A., Snyder, R., Brown, P., Eching, S., Spofford, T., Hattendorf, M., Cuenca, R.H., Wright, J.L. and Martin, D. (2000) Issues, Requirement and Challenges in Selecting and Specifying a Standardized ET Equation. Proceedings of the 4th Decennial National Irrigation Symposium of the ASAE, Phoenix, 14-16 November 2000, 201-208.
- Snyder, R.L. (1992) Equation for Evapotranspiration Pan to Evapotranspiration Conversions. Journal of Irrigation and Drainage Engineering, 118, 977-980.
- Jensen, M.E., Burman, R.D. and Allen, R.G. (1990) Evapotranspiration and Irrigation Water Requirements. ASCE Manuals and Reports on Engineering Practices No. 70, New York.
- Raghuwanshi, N.S. and Wallender, W.W. (1998) Converting from Pan Evaporation to Evapotranspiration. Journal of Irrigation and Drainage Engineering, 124, 275-277.
- Grismer, M.E. (2000) Long-Term Evapotranspiration from Coastal Avocado/Citrus Orchard. Journal of Irrigation and Drainage Engineering, 126, 1-7. http://dx.doi.org/10.1061/(ASCE)0733-9437(2000)126:1(1)
- Imtiyaz, M., Mgadla, N.P., Manase, S.K., Chendo, K. and Mothobi, E.O. (2000) Yield and Economic Return of Vegetable Crops under Variable Irrigation. Irrigation Science, 19, 87-93. http://dx.doi.org/10.1007/s002710050005
- Parmele, L.H. and Mcguiness, J.L. (1974) Comparisons of Measured and Estimated Daily Potential Evapotranspiration in a Humid Region. Journal of Hydrology, 22, 239-251. http://dx.doi.org/10.1016/0022-1694(74)90079-1 In: Amatya, D.M., Skaggs, R.W. and Gregory, J.D. (2000) Comparison of Methods for Estimating REF-ET. Journal of Irrigation and Drainage Engineering, 121, 427-435.
- Chin, D.A. and Zhao, S. (1995) Evaluation of Evapotranspiration-Pan Networks. Journal of Irrigation and Drainage Engineering, 121, 338-346. http://dx.doi.org/10.1061/(ASCE)0733-9437(1995)121:5(338)
- Singh, V.P. (1989) Volume 2: Hydrologic System. In: Raghuwanshi, N.S. and Wallender, W.W., Eds., Converting from Pan Evaporation to Evapotranspiration, Prentice-Hall, Englewood Cliffs, 275-277.
- Chiew, F.H.S., Kamaladasa, N.N., Malano, H.M. and Mcmahon, T.A. (1995) Penman-Monteith, FAO-24 Reference Crop Evapotranspiration and Class-A Pan Data in Australia. Agricultural Water Management, 28, 9-21. http://dx.doi.org/10.1016/0378-3774(95)01172-F
- Doorenbos, J. and Pruitt, W.O. (1977) Crop Water Requirements. FAO Irrigation and Drainage Papers, Rome.
- SARH (1998) Normales Climatológicas (1941-1970). Secretaría de Agricultura y Recursos Hidráulicos, México, D.F.
- Ramdas, L.A. (1957) Evaporation and Potential Evapotranspiration over the Indian Sub-Continent. The Indian Journal of Agricultural Sciences, 27, 137-149. In: Jensen, ME, Burman, RD, and Allen, R.G, (Eds.). (1990). Evapotranspiration and Irrigation Water Requirements. ASCE Manuals and Reports on Engineering Practices No. 70, New York.
- Pruit, W.O. (1966) Empirical Method of Estimating Evapotranspiration Using Primarily Evaporation Pans. Proceedings of the Conference on Evapotranspiration, Chicago, December, 57-61. In: Jensen, ME, Burman, RD, and Allen, RG. (Eds.), (1990). Evapotranspiration and Irrigation Water Requirements. ASCE Manuals and Reports on Engineering Practices No. 70, New York.
- Pruit, W.O. (1986) Traditional Methods Evapotranspiration Research Priorities for the Next Decade. American Society of Agricultural Engineers Paper No. 86-2629, 23 p. In: Jensen, ME, Burman, RD, and Allen, RG. (1990). Evapotranspiration and irrigation water requirements. ASCE manuals and reports on engineering practices No. 70, New York.