Journal of Water Resource and Protection
Vol.06 No.05(2014), Article ID:45308,11 pages
10.4236/jwarp.2014.65050
Application of Gamma Test and Neuro-Fuzzy Models in Uncertainty Analysis for Prediction of Pipeline Scouring Depth
Naser Niknia1*, Hossein Kardan Moghaddam2, S. M. Banaei3, Hassan Torabi Podeh4, Fereydoon Omidinasab5, Azam Arabi Yazdi6
1Department of Water Engineering, Lorestan University, Khoramabad, Iran
2Faculty Member of Birjand University of Technology, Birjand, Iran
3Faculty Member of Birjand University, Birjand, Iran
4Agriculture Faculty, Lorestan University, Khoramabad, Iran
5Structural Eng., Lorestan University, Khoramabad, Iran
6Agricultural Meteorology, Department of Water Engineering, Ferdowsi University of Mashad, Mashhad, Iran
Email: *naser.niknia@gmail.com, h.kardanmoghaddam@birjandut.ac.ir, smbanaie@birjand.ac.ir, torabi1976@gmail.com, omidinasab@gmail.com, azamarabi@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 28 January 2014; revised 26 February 2014; accepted 25 March 2014
ABSTRACT
The process involved in the local scour below pipelines is so complex as to make it difficult to establish a general empirical model to provide accurate estimation for scour. This paper describes the use of an adaptive neuro-fuzzy inference system (ANFIS) and a Gamma Test (GT) to estimate the submerged pipeline scour depth. The data sets of laboratory measurements were collected from published literature and used to train the network or evolve the program. The developed networks were validated by using the observations that were not involved in training. The performance of ANFIS was found to be more effective when compared with the results of regression equations and GT Network modelling in predicting the scour depth of pipelines.
Keywords:
Pipelines, Local Scour, Gamma Test, ANFIS

1. Introduction
Scour is a major cause for the failure of underwater pipeline. Interactions between the pipeline and its erodible bed under strong current and/or wave conditions may cause scouring around the pipelines. This process involves the complexities of both the three-dimensional flow pattern and the sediment movement. Scouring underneath the pipeline may expose a section of the pipe, causing it to become unsupported in the stream. If the free span of the pipe is long enough, the pipe may experience resonant flow-induced oscillations, leading to settlement and subsequently structural failure. Accurate estimate of the scour depth is important in the design of submarine pipelines [1] . The estimation of the scour characteristics of underwater pipelines continues to be a concern for hydraulic engineers.
A number of empirical formulas have been developed in the past to estimate equilibrium scour depth below pipeline, including [1] -[6] . A summary of these equations is shown in Table 1.
Predictive approaches such as artificial neural networks (ANNs) and adaptive neuro-fuzzy inference systems (ANFIS) have been recently shown to yield effective estimates of scour around hydraulic structures. ANNs have been reported to provide reasonably good solutions for hydraulic engineering problems, in cases of highly nonlinear and complex relationship among the input-output pairs in corresponding data.
The objective of this study is to develop a predictive model for scour depth, and in particular 1) to develop an ANFIS model with the aid of Gamma Test, 2) to evaluate the uncertainty inherent by using ANFIS and Gamma Test models for scour depth estimation in clear-water condition and (3) to compare the results obtained the ANFIS model with the empirical methods.
2. Local Scour below Underwater Pipelines
The variables influencing the equilibrium scour depth  below a pipeline in a steady flow over a bed of uniform, spherical and cohesion less sediment as shown in Figure 1 are: flow condition, sediment characteristics, and pipe geometry. The scour depth can be represented by the following general functional relationship:
below a pipeline in a steady flow over a bed of uniform, spherical and cohesion less sediment as shown in Figure 1 are: flow condition, sediment characteristics, and pipe geometry. The scour depth can be represented by the following general functional relationship:
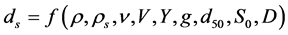 (1)
(1)
where 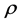 = fluid density,
= fluid density, 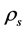 = sediment density, ν = fluid kinematic viscosity,
= sediment density, ν = fluid kinematic viscosity,  = Average velocity,
= Average velocity, 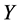 =
=
Table 1. Empirical formulae for estimate pipeline scour depth.
Figure 1. Local scour below pipeline in river crossing.
flow depth, 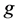 = gravitational acceleration,
= gravitational acceleration, 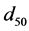 = particle mean diameter,
= particle mean diameter, 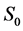 = slope of the energy line, D = diameter of the pipe, and
= slope of the energy line, D = diameter of the pipe, and  = equilibrium scour depth.
= equilibrium scour depth.
The nine independent variables in Equation (1) can be reduced to a set of six non-dimensional parameters. The Buckingham theorem applied to Equation (1), selecting  ,
,  and D as repeating variables, leads to:
and D as repeating variables, leads to:
 (2)
(2)
where  = dimensionless Shields parameter related to sediment transport;
= dimensionless Shields parameter related to sediment transport; 


Reynolds number is considered negligible under a fully turbulent flow over a rough bed ([7] [8] ). The data were collected from a number of references namely [6] [9] . The whole collected data consists of 215 data set. Table 2 shows the range of variation of collected data and its parameters.
3. Development of ANFIS
During the last two decades, researchers have noticed that the use of soft computing techniques as an alternative to conventional statistical methods based on controlled laboratory or field data has provided significantly better results. Neural network (NN) and ANFIS are the most widely used branches of soft computing in hydraulic engineering. Within the larger field of hydraulics, a few researchers have dealt with the scour around and downstream of hydraulic structures using NN [10] [11] . This study presents ANFIS and Gamma Test (GT) as an alternative tool in the prediction of scour below pipeline scour.
Therefore, the present study is based on a new soft computing technique, combined neural and fuzzy networks.
3.1. Neuro-Fuzzy System
The most important characteristics of these methods are the ability to implement human knowledge by tongue labels and fuzzy rules, nonlinearity of these systems and their adaptability [12] . It utilizes human expertise. In fuzzy systems, relationships are represented explicitly in the form of the if-then rules. In neural networks, the relations are not explicitly given, but are encoded in the designated networks and parameters. Neuro-fuzzy systems combine semantic transparency of rule-based fuzzy systems with the learning capability of neural networks. Depending on the structure of the if-then rules, two main types of fuzzy models are distinguished as mamdani (or linguistic) and Takagi-Sugeno models. The mamdani model is typically used in knowledge-based (expert) systems while the Takagi-Sugeno model is used in data-driven systems.
Table 2. Data variation.
Based on the above statements, combining of fuzzy systems, which work on logical rules, with artificial neural networks, which extract knowledge from numerical information, we can develop models that simultaneously use numerical formation and tongue statements to model any phenomenon. This combined method of artificial neural network and fuzzy systems is named the adaptive neuro-fuzzy inference system ([13] -[16] ). A fuzzy system is one based on logical rules of if-then statements. The most common type of fuzzy systems is the Sugeno fuzzy system in which fuzzy rules are stored in a rule base station. The rules in this system are

where A1 , A2 and ××× An are the fuzzy sets. In this system, if the section of the rule is a fuzzy value and the result section of the rule is a real function of the input values and usually is a linear statement such as: [17] . ANFIS network architecture is shown in Figure 2.

3.2. Training of the ANFIS Model Using Genfis2 and Genfis3
In order to begin the training an FIS structure is needed first. The FIS structure specifies the parameters of FIS system for learning. Genfis2 function meets these requirements because it generates a Sugeno-type FIS structure using subtractive clustering and requires separate sets of input and output data as input arguments. When there is only one output, Genfis2 may be used to generate an initial FIS for ANFIS training. Genfis2 accomplishes this by extracting a set of rules that models the data behavior. In order to find optimum cluster centers, several cluster radii were examined and the radius of 0.5 for clusters, proved to yield the best results [18] . Since clustering is sensitive to the range of elements in the input vector, the data set was normalized within the unit hypercube. The rule extraction method first uses the subclust function to determine the number of rules and antecedent membership functions and then uses linear least squares estimation to determine each rule’s consequent equations. This function returns a FIS structure that contains a set of fuzzy rules to cover the feature space. The numbers of rules were 9 and 18 for dimensional and non-dimensional combinations, respectively (Figure 3(a) and Figure 3(b)).
Another Fuzzy interface system using for training of the ANFIS model is Genfis3. It generates an FIS using fuzzy c-means (FCM) clustering by extracting a set of rules that models the data behavior. The function requires separate sets of input and output data as input arguments. When there is only one output, you can use genfis3 to generate an initial FIS for ANFIS training. The rule extraction method first uses the FCM function to determine the number of rules and membership functions for the antecedents and consequents. The functional set and op-
Figure 2. ANFIS network architecture.

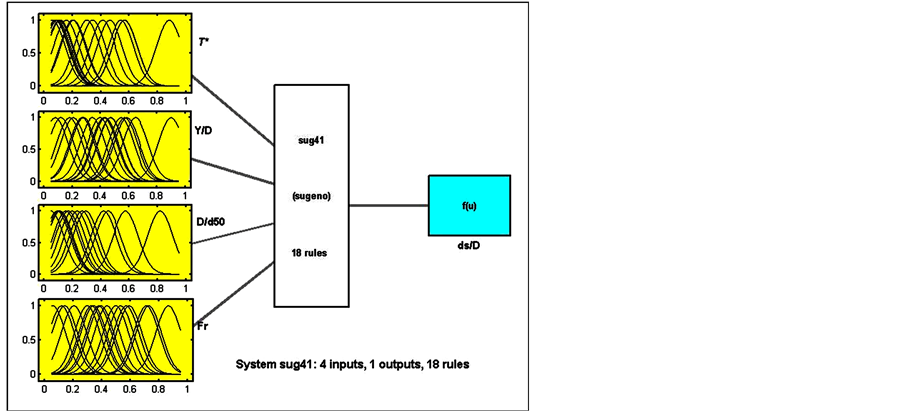
Figure 3. ANFIS models: (a) Genfis2 model; (b) Genfis3 model.
erational parameters for dimensional analysis in best combination used in the ANFIS modeling in this study are listed in Table 3.
In this study, attempts were made to improve the GT to illustrate the best combination of nonlinear model inputs prior to model construction and evaluation for selection of the best input parameter for ANFIS network and to yield a better prediction of scour depth below an underwater pipeline.
3.3. Development of ANFIS Model
How the data are presented for training is one of the most important aspects of ANN and ANFIS models. Often this can be done in more than one way [19] . The authors collected such data from several references such as [6] , [9] . The whole data set consists 215 data points. The ANFIS model was developed using the same input variables.
A code was developed in MATLAB to perform the analysis. Before applying the ANFIS algorithm, all data must be normalized. In order to normalize the data, they are transformed into the range of [0.05, 0.95]. The following formula is used for the normalization of data:

where Xn and Xr are the normalized and the original inputs; and Xmin and Xmax are the minimum and maximum of input ranges, respectively.
Out of the total of 215 input-output pairs, about 75% (161 sets), are randomly selected, were used for training, whereas the remaining 25% (54 sets) were employed for testing. Five of nine parameters in (1) namely fluid density, the buoyant sediment density, fluid dynamic viscosity, gravitational acceleration and the slope of energy line are constant in all experiments. Therefore, the first combination involves just four of the nine parameters in Equation (1) as the input pattern and the equilibrium scour depth 

been used for the ANFIS model.
4. New Input Selection Model: Gamma Test
The selection of model input variables is a complex issue, even for linear multivariable regression analysis and nonlinear models such as ANN. Choosing the optimum inputs to arrive at good predictions is important in nonlinear modeling. This paper demonstrates a new model “Gamma Test” to identify the best combination and number of input data to make a prediction with the best possible accuracy. The Gamma Test is a non-linear analysis tool which allows quantification of the extent to which a smooth relationship exists within a numerical input/output
Table 3. Parameters of ANFIS models for dimensional analysis in best combination.
data set. The Gamma Test was first reported by [20] - [21] , and later enhanced and discussed in detail by many researchers [22] - [27] . There is very limited work published using the Gamma Test in hydrology (examples include water level and flow modeling in the River Thames by [26] , daily solar radiation prediction by [28] , Daily pan evaporation modeling in a hot and dry climate by [29] and comparison of LLR, MLP, Elman, NNARX and ANFIS Models in solar radiation estimation by [30] .
The Gamma Test estimates the minimum mean square error (MSE) that can be achieved when modeling the unseen data with any continuous nonlinear models. The basic idea is quite distinct from the earlier attempts with nonlinear analysis. Suppose we have a set of data observations of the form

in which input vectors are confined to some closed bounded set 


The domain of a possible model is now restricted to the class of smooth functions which have bounded first partial derivatives. The Gamma statistic is an estimate of the model’s output variance that cannot be accounted for by a smooth data model.
The Gamma Test can estimate Var. (r) directly from the data, even though function f is unknown. This estimate is calculated by computing the following equations called a delta function:


where |…| denotes Euclidean distance, 









It can be shown that

Calculating the regression line gradient can also provide helpful information on the complexity of the system under investigation. First, it is remarkable that the vertical intercept Γ of the y- (or Gamma) axis offers an estimate of the best MSE achievable, utilizing a modeling technique for unknown smooth functions of continuous variables [31] . Second, the gradient offers an indication of model’s complexity (a steeper gradient indicates a model of greater complexity).
The Gamma Test is a non-parametric method and the results apply regardless of the particular techniques used to subsequently build a model of f . We can standardize the result by considering another term Vratio, which returns a scale invariant noise estimate between zero and one. Vratio is defined as:

where, 
5. Uncertainty Analysis
In order to measure and compare the uncertainty related to the results of ANFIS models, there needs to compare some objective criteria. In this study we used coefficient of determination (R2), root mean squared error (RMSE) and mean absolute error (MAE):



where 


Gamma Test is used to measure uncertainty by Gamma value, gradient and Vratio .This paper demonstrates all combinations of input data that affect the pipeline scour depth by using full embedding. A full embedding tries every combination of inputs to determine which combination yields the smallest absolute Gamma value. It returns the number of results requested. If there are m scalar inputs then there are 
Table 4. The sensitivity analysis for Independent Parameters for the Validation set (Genfis2).
model complexity. Vratio is the measure of predictability of given outputs using available inputs. An input data set with low values of MSE, gradient and Vratio is considered as the best scenario for the modeling. Four representative combinations for each data set (include the best one) are tabulated in Table 3. From Table 3 we can deduce that the combination of four parameters in two data sets can make a good model compared with other options. The relative importance of inputs are D > Y > u > d50 and τ* > D/d50 > Fr > Y/D for first and second combinations, respectively.
The quantity of sufficient input data to predict the desirable output was analyzed using the Gamma Test.
6. Result and Discussion
In this study, different combinations of input data (non-dimensional data sets) were explored to assess their influence on the scour depth modeling (Table 3). The ANFIS model was developed and tested for predicting the pipeline scour depth. The dimensional parameter combinations included the flow velocity; flow depth; particle mean diameter; diameter of the pipe; and the equilibrium scour depth. A dimensional analysis was used to determine the parameter for underwater pipeline scour. The Combination of non-dimensional parameters include the dimensionless Shields parameter related to sediment transport; pipeline diameter cross section of grain size (d50); and the Froude number. Each parameter (except energy slope) in Equations (1) and (2) was considered in turn in the ANFIS for the sensitivity analysis. The results show that, of the parameters in Equation (1), the mean particle size (d50) has the most significant effect on the scour depth and the flow discharge has the least effect on it.
Similarly, for non-dimensional parameters in Equation (2), sensitivity analysis shows that dimensionless Shields parameter (τ*) and Y/D have respectively the most and the least effect on normalized scour depth. The quantity of input data required to predict the desirable output was analyzed using the M-Test with various data lengths for two combinations. This shows that a training data length of 173 and 158 is sufficient for the Gamma statistics to become stable and low respectively for dimensional (original data) and non-dimensional combinations. Statistical results of different combination are in Table 5. For simulation with the ANFIS model, we generate an FIS structure from data using subtractive clustering with 9 rules. To assess the performance of the ANFIS model, observed equilibrium scour depth values are plotted against the predicted ones. Figure 4 and Figure 5 illustrate the results with the performance indices between predicted and observed data for the validating (testing) data sets, for dimensional and non-dimensional respectively. As can be seen from Table 6, the first
Table 5. Comparison of performance of the ANFIS model used based on statistical criteria.
Table 6. The Gamma Test results on the pipeline depth scour data set.
Figure 4. Observed versus predicted scour depth for dimensional parameter-validation (testing).
Figure 5. Observed versus predicted scour depth for non dimensional parameter-validation (testing).
combination (original data) has better ability to predict scour depth. The result for the original data show a high coefficient of determination (R2), also the RMSE in the second combination is better than the first combination in both training and validation periods but this variation is low compare with R2 variation. This study is useful for applications of pipeline scour for field conditions because the ANFIS model was developed with wide range of data, which could be deemed as the closest to field conditions, particularly helping to identify parameters that most likely define scour processes and explain scour variability, and ANFIS model is shown to agree well with actual measurements.
7. Conclusion
The application of a relatively new soft computing approach of ANFIS to predict the local pipeline scour depth was described. An ANFIS and GT model was developed to predict the values of the relative scour depth from laboratory measurements. A new approach was presented to estimate the equilibrium depth scour below underwater pipelines from optimum data sets with the ANFIS and GT modeling techniques. The application of the ANFIS in this study is another important contribution to scour depth estimation methodologies for pipes. The present study indicates that employing the original data set yielded a network that can predict measured pipeline scour depth more accurately than standard regression analysis based formulas [1] [3] -[6] that under- and over predict scour depths. Further work is required to collect field data of scour at pipeline to train the GP approach and validate its usefulness.
References
- Chiew, Y.M. (1991) Prediction of Maximum Scour Depth at Submarine Pipelines. Journal of Hydraulic Engineering, 117, 452-466. http://dx.doi.org/10.1061/(ASCE)0733-9429(1991)117:4(452)
- Chao, J.L. and Hennessy, P.V. (1972) Local Scour under Ocean Outfall Pipe-Lines. Water Pollut. Control Fed., 44, 1443-1447.
- Kjeldsen, S.P., Gjørsvik, O., Bringaker, K.G. and Jacobsen, J. (1973) Local Scour near Offshore Pipelines. Proc., 2nd Int. Conf. on Port and Ocean Engineering under Arctic Conditions, Univ. of Iceland, 308-331.
- Ibrahim, A. and Nalluri, C. (1986) Scour Prediction around Marine Pipelines. Proc., 5th Int. Symp. On offshore Mechanics and Arctic Engineering, 679-684.
- Bijker, E.W. and Leeuwestein, W. (1984) Interaction between Pipelines and the Seabed under Influence of Waves and Currents. Proc., Symp. on Int. Union of Theoretical Applied Mechanics/Int. Union of Geology and Geophys., 235-242.
- Moncada-M., A.T. and Aguirre-Pe, J. (1999) Scour below Pipeline in River Crossings. Journal of Hydraulic Engineering, 125, 953-958. http://dx.doi.org/10.1061/(ASCE)0733-9429(1999)125:9(953)
- Lim, F.H. and Chiew, Y.M. (2001) Parametric Study of Riprap Failure around Bridge Piers. Journal of Hydraulic Research, 39, 61-72. http://dx.doi.org/10.1080/00221680109499803
- Melville, B.W. (1992) Local Scour at Bridge Abutments. Journal of Hydraulic Engineering, 118, 615-631. http://dx.doi.org/10.1061/(ASCE)0733-9429(1992)118:4(615)
- Dey, S., and Singh, N.P. (2008) Clear-Water Scour below Underwater Pipelines under Steady Flow. Journal of Hydraulic Engineering, 134, 588-600. http://dx.doi.org/10.1061/(ASCE)0733-9429(2008)134:5(588)
- Liriano, S.L. and Day, R.A. (2001) Prediction of Scour Depth at Culvert Outlets Using Neural Networks. J. Hydro informatics, 3, 231-238.
- Kambekar, A.R. and Deo, M.C., (2003) Scour Estimation of Pile Group Using Neural Networks. Applied Ocean Research, 25, 225-234. http://dx.doi.org/10.1016/j.apor.2003.06.001
- Jang, J.S.R. (1993) ANFIS: Adaptive-Network-Based Fuzzy Inference System. IEEE Transactions on Systems, Man, and Cybernetics, 23, 665-685. http://dx.doi.org/10.1016/j.apor.2003.06.001
- Jang, J.S.R. and Gulley, N. (1995) The Fuzzy Logic Toolbox for Use with MATLAB. The Mathworks Inc., Natick.
- Kisi, O., Karahan, M.E. and Sen, Z., (2006) River Suspended Sediment Modeling Using a Fuzzy Logic Approach. Hydrological Processes, 20, 4351-4362. http://dx.doi.org/10.1002/hyp.6166
- Gopakumar, R.P. and Mujumdar, P. (2007) A Fuzzy Dynamic Wave Routing Model. Hydrological Processes, 21, 458-467.
- Şen, Z. and Altunkaynak, A. (2006) A Comparative Fuzzy Logic Approach to Runoff Coefficient and Runoff Estimation. Hydrological Processes, 20, 1993-2009. http://dx.doi.org/10.1002/hyp.5992
- Madvar, H.R., Ayyoubzadeh, S.A. and Khadangi, E. (2009) An Expert System for Predicting Longitudinal Dispersion Coefficient in Natural Streams by Using ANFIS. Expert Systems with Applications, 43, 1016-1024.
- Talebizadeh, M. and Moridnejad, A. (2011) Uncertainty Analysis for the Forecast of Lake Level Fluctuations Using Ensembles of ANN and ANFIS Models. Expert Systems with Applications, 38, 4126-4135. http://dx.doi.org/10.1016/j.eswa.2010.09.075
- Bateni, S.M., Borghei, S.M. and Jeng, D.S., (2007) Neural Network and Neuro-Fuzzy Assessments for Scour Depth around Bridge Piers. Engineering Applications of Artificial Intelligence, 20, 401-414. http://dx.doi.org/10.1016/j.engappai.2006.06.012
- Končar, N. (1997) Optimization Methodologies for Direct Inverse Neuro Control. Ph.D. Thesis, Department of Computing, Imperial College of Science, Technology and Medicine, University of London, London.
- Agalbjörn, S., Končar, N. and Jones, A.J. (1997) A Note on the Gamma Test. Neural Computing and Applications, 5, 131-133. http://dx.doi.org/10.1007/BF01413858
- Chuzhanova, N.A., Jones, A.J. and Margetts, S. (1998) Feature Selection for Genetic Sequence Classification. Bioinformatics, 14, 139-143. http://dx.doi.org/10.1093/bioinformatics/14.2.139
- De Oliveira, A.G. (1999) Synchronization of Chaos and Applications to Secure Communications. Ph.D. Thesis, Department of Computing, Imperial College of Science, Technology and Medicine, University of London, London.
- Tsui, A.P.M. (1999) Smooth Data Modelling and Stimulus-Response via Stabilization of Neural Chaos. Ph.D. Thesis, Department of Computing, Imperial College of Science, Technology and Medicine, University of London, London.
- Tsui, A.P.M., Jones, A.J. and de Oliveira, A.G. (2002) The Construction of Smooth Models Using Irregularembedding’s Determined by a Gamma Test Analysis. Neural Computing and Applications, 10, 318-329. http://dx.doi.org/10.1007/s005210200004
- Durrant, P.J. (2001) WinGamma: A Non-Linear Data Analysis and Modelling Tool with Applications to Flood Prediction. Ph.D. Thesis, Department of Computer Science, Cardiff University, Cardiff.
- Jones, A.J., Tsui, A. and de Oliveira, A.G. (2002) Neural Models of Arbitrary Chaotic Systems: Construction and the Role of Time Delayed Feedback in Control and Synchronization. Complexity International, 09.
- Remesan, R., Shamim, M.A. and Han, D. (2008) Model Data Selection Using Gamma Test for Daily Solar Radiation Estimation. Hydrological Processes, 22, 4301-4309. http://dx.doi.org/10.1002/hyp.7044
- Piri, J., Amin, S., Moghaddamnia, A., Keshavarz, A., Han, D. and Remesan, R. (2009) Daily Pan Evaporation Modeling in a Hot and Dry Climate. Journal of Hydrological Engineering, 14, 803-811.
- Moghaddamnia, A., Remesan, R., Hassanpour Kashani, M., Mohammadi, M., Han, D. and Piri, J. (2009) Comparison of LLR, MLP, Elman, NNARX and ANFIS Models—With a Case Study in Solar Radiation Estimation. Atmospheric and Solar-Terrestrial Physics, 71, 975-982. http://dx.doi.org/10.1016/j.jastp.2009.04.009
- Evans, D. and Jones, A.J. (2002) A Proof of the Gamma Test. Proceedings of Royal Society, 458, 2759-2799. http://dx.doi.org/10.1098/rspa.2002.1010
NOTES
*Corresponding author.








