Journal of Water Resource and Protection
Vol. 3 No. 7 (2011) , Article ID: 6320 , 14 pages DOI:10.4236/jwarp.2011.37065
Hydrogeochemical Evolution and Groundwater Flow in the Densu River Basin, Ghana
1Graduate School of Nuclear and Allied Sciences, University of Ghana, Accra, Ghana
2Nuclear Chemistry and Environmental Research Centre, National Nuclear Research Institute, Ghana Atomic Energy Commission, Accra, Ghana
3Institute of Groundwater Ecology, German Research Centre for Environmental Health, Neuherberg, Germany
E-mail: dadomako@fastmail.fm
Received March 31, 2011; revised May 12, 2011; accepted June 28, 2011
Keywords: Densu, Groundwater, Oxygen-18, Deuterium
ABSTRACT
Groundwater resources play a crucial role in the domestic and industrial water delivery system in Ghana. Hydrochemical and multivariate statistical techniques were used to investigate groundwater flow and geochemical evolution in the Densu River Basin aquifer system in Ghana. The hydrochemical and multivariate statistical techniques are mutually supportive and extracted information was analysed together with environmental isotope data. The results reveal three spatial groundwater bodies with defined hydrochemical facies, residence times, stable isotopic signals and hydrochemical evolution. The zones are designated as group one in the northern portion, group two in the transmission zone and group three as discharge in the southern portion of the catchment. Some of the stable isotope data of the groundwater do not lie close to the local meteoric water line (LMWL) on the δD-δ18O plot and thus indicate that the meteoric water recharging the groundwater system has undergone some degree of evaporation.
1. Introduction
Groundwater is one of the most important resources in Ghana. In many rural and urban communities in the Densu River basin, water supplies for domestic, irrigation and industrial uses are primarily dependent on existing groundwater resources. However, groundwater potential is under serious treat, due to increasing population density, mechanized agricultural practices, rapid urbanization, as well as domestic and industrial usage. Groundwater provision is time and again unsuccessful because of poor groundwater productivity of wells, drying of wells after prolonged draught or sometimes due to poor quality. The latter is hampered by lack of understanding the groundwater systems. However, groundwater resources in the Densu River basin have been fairly assessed and some data on the geology, borehole yield, static water levels and water quality analysis are available [1]. A large amount of hydrogeological and hydrochemical data have been generated through drilling activities in the basin. Nonetheless, due to lack of harmonized database, not much has been done to understand the hydrogeological and the hydrochemistry of the aquifers as a means of understanding the chemical evolution of groundwater system in the basin.
The changes in chemical composition of meteoric water recharging the aquifer will depend on factors such as soil-water interaction, residence time, congruent and incongruent dissolution of mineral assemblages, seawater intrusions and anthropogenic impacts. These factors would give rise to different water chemistry and hence different aquifer characteristics [2-5]. Additionally, in groundwater catchments where barrier boundaries and inputs are well defined, interpretation of the environmental isotopes record of precipitation, surface water and groundwater, coupled with available information on hydrochemical characteristics of groundwater will provide a detailed picture of the groundwater system [6,7].
Therefore, in other to understand the geochemical characteristics of the groundwater system, and its flow regime, multivariate statistical tools have been used widely to study the sources of the variation in the hydrochemistry of groundwater systems in recent studies. Arguably, one of the most powerful tools that have gained widespread acceptance in geo-environmental research community is multivariate statistical hydrochemical modelling. Precisely, factor and cluster analysis are the most widely used tools in geochemical studies to understand trends in data variation. Excellent examples of the application of factor analysis to solve hydrochemical problems are contained in [8-10]. Additionally, multivariate techniques have been used to resolve hydrological factors such as aquifer boundaries, groundwater flow paths and geochemical parameters e.g. [11,12]. It has also been used to identify geochemical controls on the composition of water [13], and separate anomalies such as anthropogenic impacts from background concentrations e.g. [14,15]. The specific objectives of this work are: 1) to understand the geochemistry and flow mechanisms of groundwater in the catchment, and 2) to characterize the isotopic (δ18O, δD) compositions of groundwater.
2. Materials and Methods
2.1. Study Area
2.1.1. Location
The Densu River Basin is located in the southwestern side of Ghana. The Basin is characterized by undulating topography. Many of the hills here are craggy summits, which give a striking appearance to the landscape. The Densu River Basin lies between latitude 5˚30'N - 6˚20'N and longitude 0˚10'W - 0˚35'W (Figure 1). The Densu River Basin is coastal river catchments in the southern Ghana, and a typical rural community like all other rural settlements in Ghana. The Basin has a catchment area of 2,564 km2 and spans 10 district assemblies and three regions of Ghana, namely Eastern, GreaterAccra and Central. There are about 200 settlements in the basin with a population density ranging from 150 to 200 per square kilometre, which is above the national average of 77 persons per square kilometre [16]. The river takes its source from the Atewa Range near Kibi in the East Akim Metropolitan Assembly, in the Eastern Region of Ghana and flows for 116 km from this source at an elevation of about 760 m (2,500 ft.) above sea level. The main tributaries of the river include Mame, Kuia, Adeiso, Dobro and Nsaki rivers. The river shares its catchment boundary with the Odaw and Volta basins to the east and north respectively, the Birim basin in the northwest and the Ayensu and Okrudu in the west. The river then enters the Gulf of Guinea through the tidal lagoon at Botianor, west of Accra.
2.1.2. Climate
The study area lies between two distinct climatic zones; the dry equatorial climate of the SE coastal plains, and the wet semi-equatorial climate further north from the coast. Both climatic zones are characterised by two rainfall seasons with different intensities [17]. The major rainy season extends from April/May to July and attains a peak in June when the maritime instability causes a surge of the moist south-westerly air stream resulting in the intensification of the monsoon rain. The minor season occurs between September and November when several disturbance lines give rise to local thunder activities, especially in the upper and middle belts which are covered with moist semi-deciduous forest. The total annual rainfall ranges from 1700 mm in the wet interior to 800 mm in the dry equatorial zone near the coast.
The climate of the study area is also characterised by prevailing high temperatures usually uniformly high throughout the year. The mean annual temperature is reported as 27˚C, with March/April being the hottest (32˚C) and August the coolest (23˚C). The maximum and minimum relative humidity values vary from 89% to 93% and 41 to 72% respectively.
2.1.3. Geological Setting
The Densu River Basin is underlain mainly by the Proterozoic basin-type granitoid (the so-called Cape Coast batholiths), granite with associate gneiss. This geological formation covers a larger part of the basin (90%) as shown in Figure 1. The other formations are the Birimian formation, which occurs at the watershed of the river in the northwest, covering approximately 4% of the basin. The Togo Formation (6%) underlies the southeastern portion and the area south of Weija to the estuary portion of the basin. The Cape Coast granite Complex comprises heterogeneous group of rocks occupying most of the northwestern corner of the Akwapim North and part of Akwapim South districts. The bulk of the Cape Coast granite is composed of quartz, muscovite, orthoclase and albite. The granite changes from fine to medium grained, foliated biotite quartz diorite gneiss to hornblende–quartz diorite gneiss. These gneissic rocks are intruded by both acidic and basic igneous rocks, which include white and pink Pegmatite, aplites, granodiorite and peridotite.
Traditionally, [18,19] subdivided the Birimian Supergroup into two parts, the Lower Birimian, consisting mainly of dacitic/rhyodacitic volcaniclastics, greywackes, phyllites, argillites and chemical sediments [20], and the Upper Birimian, mainly made up of tholeiitic basalts with intercalated volcaniclastics, pyroclastic lava, and hypabyssal basic intrusive. Most of the rocks have been metamorphosed into calcareous chlorite schists and amphibolites (greenstones). Rocks belonging to the Birimian formation are sandstones, tuffs, grit, quartzites and some

Figure 1. Map showing the sampling points in the study area.
breccia. The rocks of the Togo Series are highly folded and jointed, and form the chain of hills known as the Akwapim-Togo Ranges, which extend from the coast near Accra to the Togo border. The Togo Series consists of sandstone, quartzite and quartz schist, shale, phyllite and some talc mica schist.
2.1.4. Hydrogeology
The basement rocks underlying about 90% of the Densu River Basin have very little intergranular pore-space and are thus characterised by little or negligible primary porosity and permeability. Also, because of their limited transmissivity, crystalline basement aquifer exhibit comparatively low yields [21-24]. The two main features controlling groundwater occurrence in the basin are the secondary formed fractured and weathered zones respectively. The Birimian formation to the northwestern portion of the basin are generally well folded and deeply weathered, hence groundwater occurrence in this formation is very high. The granites in the basin are less fractured and weathered, hence groundwater occurrence are moderately low. The granitic aquifers thus formed are usually phreatic to semi-confined in character, structurally dependent and may be discontinuous in occurrence. However, in the northern portion of the granitic formation relatively high productive wells exist. The Togo series in the Southeastern portion of the basin is highly folded, jointed and fractured. The contact zone between the granites and the Togo formation provides a favourable condition for groundwater accumulation.
The depth of the borehole varies from 9.1 to 103.0 m in the granites, 23.0 to 40.0 m in the Birimian and 28.0 to 97.0 m in the Togo series [25]. The thickness of the mean weathered zone ranges from 1.0 and 32.0 m, 5.0 and 27.0 m and 3.0 and 36.0 m in the granites, Birimian and Togo series respectively. The static water level also ranges from 0.1 and 13.5 m, 0.8 and 16.9 m and 1.1 and 17.9 m in the granites, Birimian and Togo series respectively. Borehole yields are highly variable and lie in the range of 0.1 - 30.0 m3·h–1 with mean value of 2.0 m3·h–1 in the granite. In the Togo and the Birimian borehole yields are within 0.6 - 6.0 m3·h–1 and 0.7 - 9.0 m3·h–1 with the mean values of 2.8 m3·h–1 and 3.7 m3·h–1 respectively. The analytical results of groundwater chemistry and groundwater level data from the Basin show that groundwater is being recharged in the northern portion and flows to the southern portion of the basin. This is because the groundwater in the northern portion is characterized by low physio-chemical and chemical parameters, and these values increases along the flow line. Borehole yields in the basin however, vary from location to location; the water potential in the wells also varies from well to well [25].
2.1.5. Field Investigations
A total of 51 groundwater water samples were taken from the aquifers across the catchment during the period of August 2006, February and May-June 2007. The samples were collected from wells (Figure 1) at depth ranging between 24 and 65 m. Standard procedures with regard to well purging were followed for collection of the groundwater samples. The geographical location of all sampling sites was recorded using a hand-held global positioning system (GPS).
Alkalinity and physical parameters such as Electrical conductivity (EC), Total Dissolved Solids (TDS), temperature and pH of the samples were measured in the field using Hatch field titration kit and portable EC and pH meters. For groundwater samples, boreholes were purged until stable readings for the physical parameters were obtained. Samples were subsequently filtered through 0.45 um membranes and collected in acidwashed, well rinsed polyethylene bottles. Filtered and acidified (1% v/v HNO3) sampled were used for major cations, while filtered unacidified sampled were used for anion analysis. Unfiltered groundwater samples were collected in 30 ml glass bottles and tightly sealed for stable isotope analysis. Other samples were collected in 1 litre polyethylene bottles and preserved for tritium analysis.
2.1.6. Laboratory Analyses
Chemical and isotopic analysis of the water samples were performed at the Institute of Groundwater Ecology, German Research Center for Environmental Health (Neuherberg/Germany). Major cations (Ca2+, Mg2+, Na+, and K+) and anions (Cl–,  , and
, and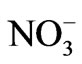 ) were analyzed using a Dionex DX 100 ion chromatograph equipped with a CS 12 and an AS14A-SC Ion Pac columns and an AS-40 auto-sampler. The accuracy of the duplicate analyses was estimated from the ionic balance error [26], which was within ±5% (3σ) for all samples.
) were analyzed using a Dionex DX 100 ion chromatograph equipped with a CS 12 and an AS14A-SC Ion Pac columns and an AS-40 auto-sampler. The accuracy of the duplicate analyses was estimated from the ionic balance error [26], which was within ±5% (3σ) for all samples.
Stable isotopes of oxygen and hydrogen were determined using isotope mass spectrometry. The water samples for oxygen isotopic analyses were prepared by conventional H2O - CO2 equilibration [27] where 5ml of each sample was equilibrated with CO2 gas at 25 ± 0.1˚C for 24 hours. The CO2 gas was then extracted and cryogenically purified in a vacuum line. For deuterium analysis, Cr at 850˚C was used to produce hydrogen gas [28]. Both δ18O and δ2H values were determined relative to internal standards that were calibrated using Vienna-Standard Mean Ocean Water (V-SMOW). The data were normalized following [29] as follows:
δ = [(RS/RV-SMOW) – 1] × 1000; where RS represents either the 18O/16O or the 2H/1H ratio of the sample, and RV-SMOW is 18O/16O or the 2H/1H ratio of the V-SMOW. The analytical reproducibility is ±0.1% and ±1.0% for the oxygen and deuterium, respectively.
2.2. Multivariate Analysis
Multivariate analysis of the water quality data sets were performed using Cluster analysis (CA), Factor Analysis (FA) and Discriminant Analysis (DA) using Statistical Package for Social Sciences (SPSS 16.0) software package for windows.
2.2.1. Cluster Analysis
CA has been used by several researchers to classify a set of observed hydrochemical data within two or more mutually exclusive groups based on the combination of interval variables [10,30,31]. The Ward method [32] of hierarchical clustering is used for the factor scores. The Ward method applies clustering in such a way as to minimize the increment of the error sum of squares (IESS). The value of error sum of squares (ESS) for the i-th cluster is given by
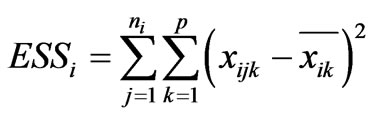
where,  is the coordinate of the observation on the p variables for nj, objects in the i-th cluster
is the coordinate of the observation on the p variables for nj, objects in the i-th cluster  is the coordinate for the centroid in the i-th cluster, j is the number of samples, k is the number of variables. The total ESS for the total number of clusters g then can be obtained by summing ESSi for i = 1 to g:
is the coordinate for the centroid in the i-th cluster, j is the number of samples, k is the number of variables. The total ESS for the total number of clusters g then can be obtained by summing ESSi for i = 1 to g: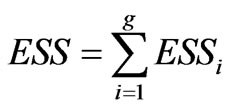 .
.
When two clusters U and V are combined to form a new cluster, the IESS can be computed by
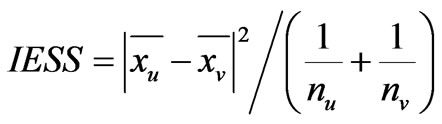
where, 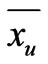 and
and 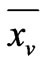 are the vectors for the centroid in the u-th cluster and in the v-th cluster, and
are the vectors for the centroid in the u-th cluster and in the v-th cluster, and 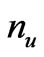 and
and 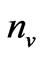 are the numbers of objects in U and V, respectively.
are the numbers of objects in U and V, respectively.
There are two modes of investigations namely R and Q-modes respectively. The R-mode is used to investigate the group associations or the affinity between the various variables in order to investigate their sources and processes with which they are associated [33]. The data set was further analyzed in Q-mode in order to identify similarities between cases. The similarity coefficient used was the simple distance defined in Euclidean space [34] and the clustering was performed by the average linkage (between-groups) method. The output results (water groups in the form of dendrogram) from the Hierarchical Cluster Analysis (HCA) are interpreted. Data treatment procedures and detailed explanation of the HCA clustering technique used by this study can be found in [30].
HCA was used to classify groundwater chemistry into logical groups that may be interpreted in terms of aquifer types, subsurface residence times and anthropogenic input on groundwater chemistry [13,35,36]. These techniques provides a good opportunity to identify relatively distinct paths for hydrochemical modeling and to understand geochemical evolution for a given aquifer system.
2.2.2. Factor Analysis
Factor analysis is a technique that purports to explain observed relations among several variates in terms of simpler relations that provide insight into the underlying structure of the variates. The factor analysis has also been used extensively in many geochemical studies to better understand the group associations or the affinity between the various variables that has been revealed by the cluster [8,34,37,38]. The simpler relations that are expressed in terms of a new set of variables are called factors.
In factor analysis, the observable random vector x, with p components, has mean µ and covariance matrix Σ. The factor model postulates that x is linearly dependent upon a few unobservable random variables F1, F2, F3,  , Fn, called common factors, and p additional sources of variation ε1, ε2,
, Fn, called common factors, and p additional sources of variation ε1, ε2,  , εp, called errors or sometimes, specific factors. The factor analysis model is represented in matrix notion.
, εp, called errors or sometimes, specific factors. The factor analysis model is represented in matrix notion.

where, the matrix L is the matrix of factor loadings, the coefficient lij of L is called the loading of the i-th variable on the j-th factor, and F is the column vector components F1, F2, F3,  , Fm. When independence assumptions about the random vectors F and ε are used, the relation (Equation (5.13)) constitutes the orthogonal factor model.
, Fm. When independence assumptions about the random vectors F and ε are used, the relation (Equation (5.13)) constitutes the orthogonal factor model.
To perform factor analysis, the first step is to compute a correlation matrix. This involves finding the correlation coefficient, which is a measure of interaction for all pairs of constituents. The second step in factor analysis is to estimate the factor loadings. The final step is to obtain easy interpretation of factors by factor rotation.
In this study, the principal component method is used as the parameter estimation method to transform a set of observed interdependent variables into an orthogonal set of variables called principal components. The first component accounts for as much as possible of the variances of the observed variates. The second principal component accounts for as much as possible of residual variance not accounted for by the first principal component. The third principal component also accounts for residual variance not accounted for by the second component.
Although numerous rotation schemes have been proposed, Kaiser’s scheme called varimax rotation is used in this study. Varimax rotation yields a set of loadings such that the variance of the squares of the loadings is the maximum. Factor scores are commonly obtained by two approaches: the weighted least squares method and the regression method. The regression method [39] was used in this study to compute factor scores.
2.2.3. Discriminant Analysis
Discriminant analysis is a multicomponent statistical technique that has been used in many geochemical studies [8,34,37,38,40] to classify groundwater into mutually exclusive and exhaustive groups on the basis of a set of independent variables. The linear combinations of the independent variables found by means of this technique will discriminate the groups in such a way that the misclassification error rates are minimized. The objective was achieved by maximizing the between-group variance to the within-group variance [41].
To perform the discriminant analysis we need a qualitative dependent variable and a set of independent variables. The categorical-dependent variable is a grouping factor that allows each object to be placed in only one of the defined groups. In the linear discriminant equation;

where,  are the values of the independent variables, and
are the values of the independent variables, and 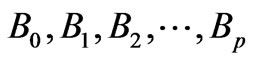 are the coefficients estimated from the data. The obtained function allows discriminating in the best way among the objects belonging to different groups; it therefore constitutes itself as a quality index, which integrates all the available information into a single variable [42].
are the coefficients estimated from the data. The obtained function allows discriminating in the best way among the objects belonging to different groups; it therefore constitutes itself as a quality index, which integrates all the available information into a single variable [42].
3. Results and Discussions
The groundwater pH is acid to circum-neutral and ranges from 5.3 and 7.2 with a mean value of 6.4. The temperatures are generally close to that of ambient temperature, 25.1 to 31.3˚C, with a mean value of 27.8˚C. The aquifer water presents wide variations in the total dissolved solids (TDS) and the electrical conductivity (EC) values; they ranges from 46 to 3890 mg/l and 99 to 8580 μS/cm, respectively and mean values are 601 mg/l and 1288 μS/cm. The high TDS and EC values of the groundwater samples in the study area follows the flow direction, thus from high to relatively low topographic areas towards the coast.
3.1. Statistical and Cluster Analysis
The SPSS 16.0 for windows statistical tool was utilized to support the conventional hydrochemical techniques. Twelve hydrochemical variables (EC, TDS, and pH, Temperature, Na+, K+, Ca2+, Mg2+, Cl–, 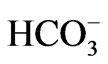 ,
, 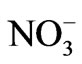 and
and ) were used in the statistical analyses. All the data were transformed to log base 10 values and subsequently standardized to their standard scores (z-cores) as outlined by [31]. For the R-mode, weighted pair-group method was applied and Euclidean distance was used as a measure of similarity. Before the analysis could be done, the data was normalised by generating a correlation coefficient matrix. The cluster revealed two distinct groups or clusters, and different clusters and their members were extracted as follows: cluster one includes EC, TDS, Na, SO4, Cl, Mg, Ca, and K, while cluster two includes pH, HCO3, temp, and NO3. Furthermore, each variable measured via different units was rescaled to a range of 0 - 1 in order to have equal weight for the hierarchical cluster analysis (HCA). The result of the HCA of the hydrochemical classification is presented as a dendrogram in Figure 2. Based on the clusters, the groundwater samples in the study area were classified into three major groups. The mean water chemistry of the groups is given in Table 1, and their physical significance of the results is tested by relating the statistically defined clusters with their geographical locations. The most distinguishing factor between major groups seems to be TDS with concentrations increasing in both cations and anions, except
) were used in the statistical analyses. All the data were transformed to log base 10 values and subsequently standardized to their standard scores (z-cores) as outlined by [31]. For the R-mode, weighted pair-group method was applied and Euclidean distance was used as a measure of similarity. Before the analysis could be done, the data was normalised by generating a correlation coefficient matrix. The cluster revealed two distinct groups or clusters, and different clusters and their members were extracted as follows: cluster one includes EC, TDS, Na, SO4, Cl, Mg, Ca, and K, while cluster two includes pH, HCO3, temp, and NO3. Furthermore, each variable measured via different units was rescaled to a range of 0 - 1 in order to have equal weight for the hierarchical cluster analysis (HCA). The result of the HCA of the hydrochemical classification is presented as a dendrogram in Figure 2. Based on the clusters, the groundwater samples in the study area were classified into three major groups. The mean water chemistry of the groups is given in Table 1, and their physical significance of the results is tested by relating the statistically defined clusters with their geographical locations. The most distinguishing factor between major groups seems to be TDS with concentrations increasing in both cations and anions, except 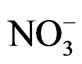 in the following order:
in the following order:

Figure 2. Dendrogram of HCA, including all water samples. The cluster analysis is based on parameters, Temp., TDS, EC, pH, Na+, K+, Mg2+, Ca2+, 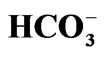 ,
,  , Cl– and
, Cl– and . The water samples are linked into clusters on the x-axis and the linkage distance is plotted on the y-axis.
. The water samples are linked into clusters on the x-axis and the linkage distance is plotted on the y-axis.
group 1, group 2 and group 3.
3.2. Factor Analysis
The log-transformed data set was subjected to principal component analysis (PCA). The suitability of the data set for the analysis was assessed by Kaiser-Meyer-Oklin (KMO). The KMO value was 0.808, exceeding the recommended value of 0.6 [43]. Also, varimax rotation was performed to enhance group separation. The first three principal component extracted explain 80.86% of the variance in the data set. It is observed from Table 2 that variables load fairly on only one component, thereby revealing a simple structure. Ca2+, EC, TDS, K+, 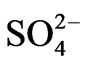 , Na+, Mg2+ and Cl– are loaded in the first principal component, pH and
, Na+, Mg2+ and Cl– are loaded in the first principal component, pH and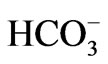 , are loaded in the second component, and temperature and
, are loaded in the second component, and temperature and 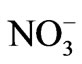 are loaded in the third component. The 12 constituents are treated as 11
are loaded in the third component. The 12 constituents are treated as 11
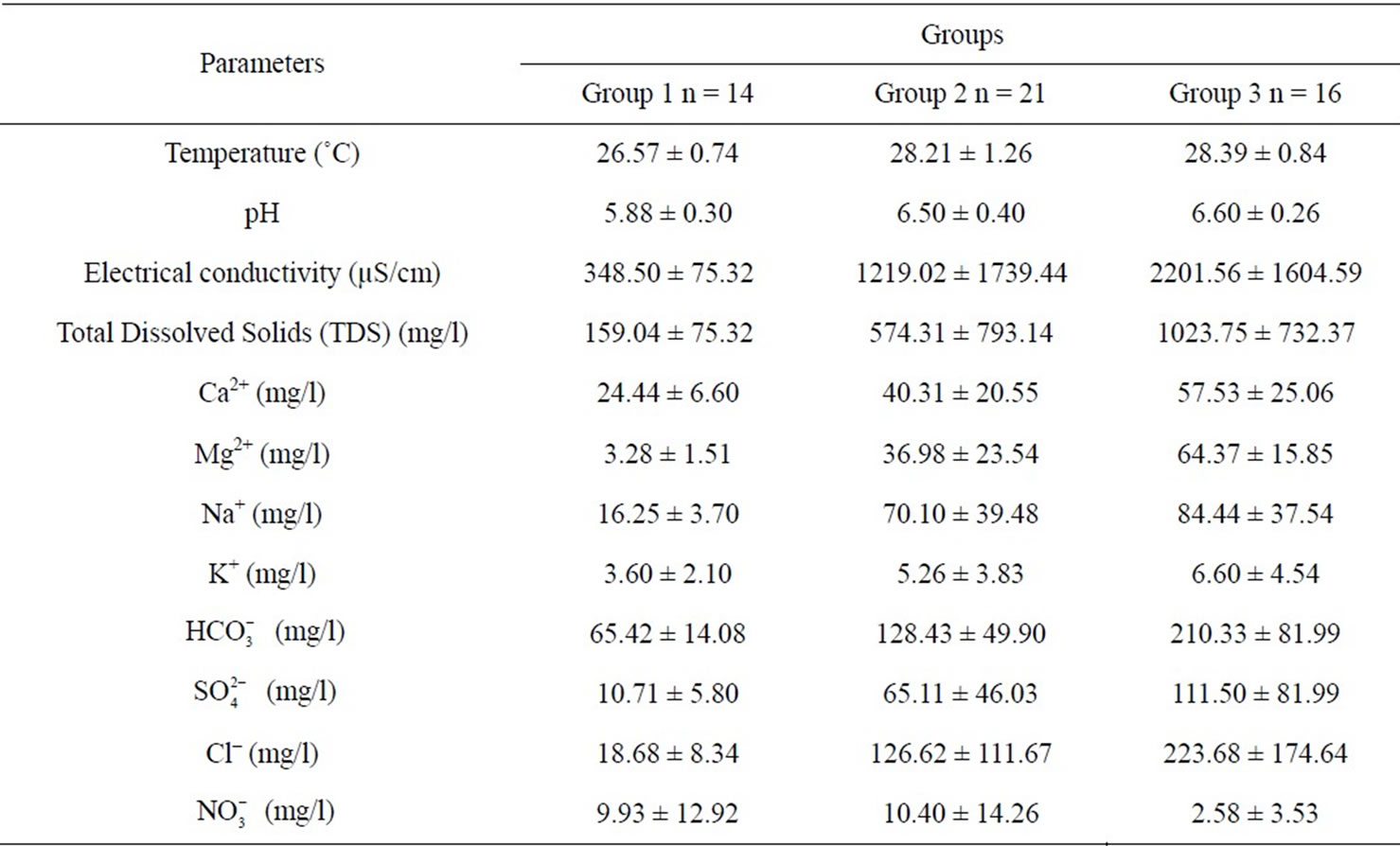
Table 1. Mean parameter composition and their corresponding standard deviation for the three groups of groundwater in the study area defined by HCA.

Table 2. Factor loading matrix for the data set after varimax rotation.
observable quantity variables with which the covariance matrix is composed for the multivariate analysis. Table 3 shows the eigen values representing factors, the eigen value, difference between factors, and the proportion of total sample variance explained by the factors. The correlation matrix among the 12 physico-chemical variables of the groundwaters were presented in Table 4. A strong correlation was observed between EC and TDS, EC and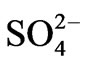 , EC and Cl–, TDS and
, EC and Cl–, TDS and , TDS and Cl–, Na+ and
, TDS and Cl–, Na+ and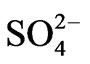 , Na+ and Cl–, Na+ and
, Na+ and Cl–, Na+ and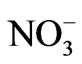 ,
,  and Cl-.
and Cl-.
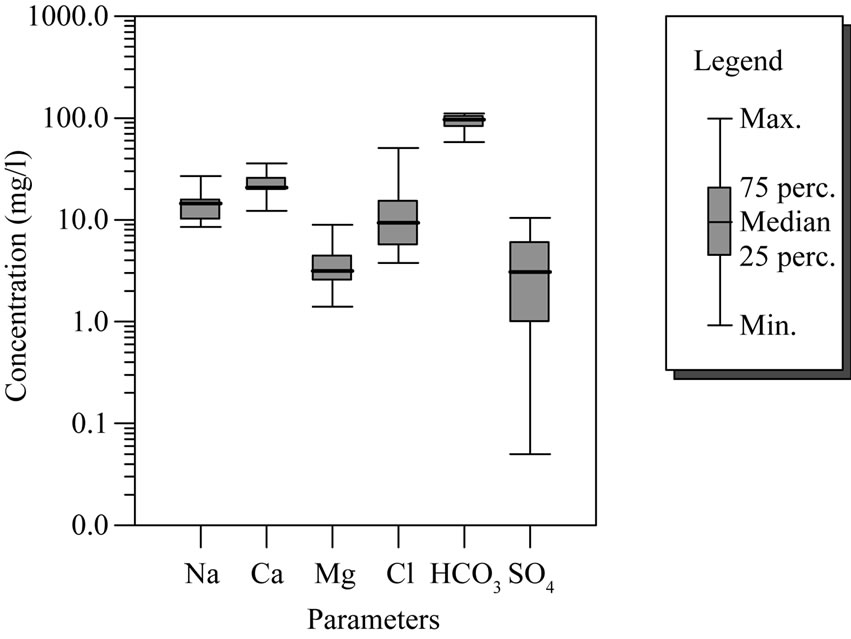
In Figures 3(a), (b) and (c), the major ion chemistry of groundwater in the study area for the various groups is summarized in three boxplots showing maximum, minimum, median, and the 25th and 75th percentile. The figure shows a wide range in concentrations for both plots, reflecting different water bodies. Group three groundwater samples have mean elevated concentration of 189.05 and 1009.50 mg/l for Cl- and TDS. This may suggest dissolution of soluble salts.
3.3. Discriminant Analysis
Discriminant analysis was performed on the log-transformed data set to assess group validity for the groundwater samples in the study area. The sample ID was used as a basis for the groups for the samples. Mahalanobis distance-derived properties were used for group membership. Linear discrimination analysis (LDA) with cross-validation correctly classified 96.1% of the cases. Figure 4 shows the groupings of the cases defined by the discriminant scores. Only two sampling points SSK-01 and GAD-11 were predicted to group one and three respectively, with their actual group being group two. In order to identify the variables that are most important in discriminating among the groups, step-wise discriminant analysis (SDA), with cross-validation were carried out with probabilities of F-to-enter-of 0.05 and F-to-remove of 0.10, 98.0% were classified by SDA. In all, a maximum number of 24 steps were employed. Temp., Ca2+,

Table 3. Eigenvalues of factors extracted through PCA, difference between factors, and proportion of variance explained by factors.

Table 4. Correlation matrix among 12 physico-chemical variables of groundwatera.
 (a)
(a)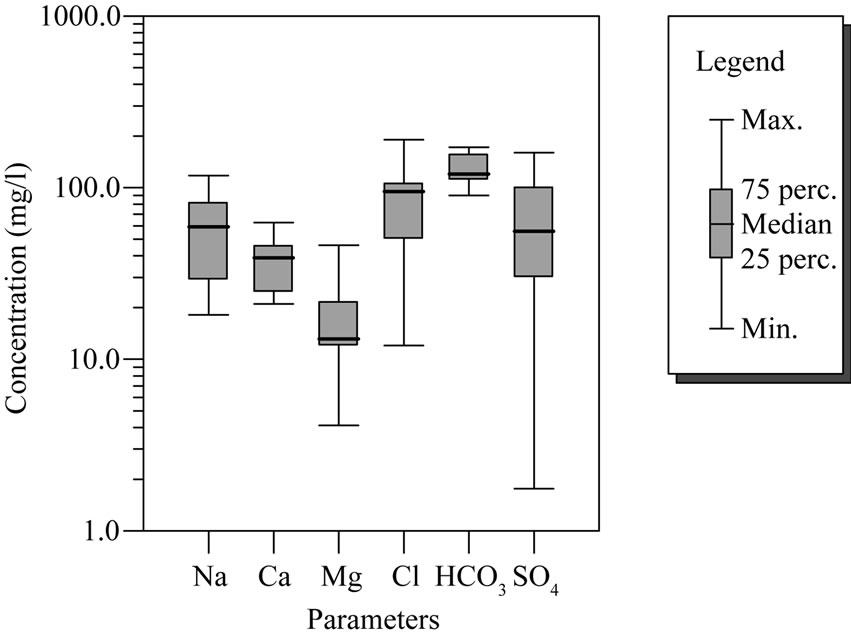 (b)
(b) (c)
(c)
Figure 3. (a) Box plots of concentrations for major elements in groundwater samples from group one; (b) Box plots of concentrations for major elements in groundwater samples from group two; (c) Boxplots of concentrations for major elements in groundwater samples from groups one, two and three respectively.
Mg2+, 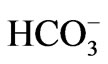 , Cl– and
, Cl– and 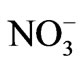 were identify as the most discriminating variables for grouping the groundwater samples in the study area. About 90% of groups one, two and three of the groundwater samples in the study area are from the northern, central and southern portions of the study area respectively.
were identify as the most discriminating variables for grouping the groundwater samples in the study area. About 90% of groups one, two and three of the groundwater samples in the study area are from the northern, central and southern portions of the study area respectively.
3.4. Hydrochemical Facies
The chemical composition of groundwater samples in the Densu River basin is shown in Figure 6. The majority of the groundwater samples in group one of the study area are characterized by low TDS and Ca-HCO3 water type (Figure 5). In most groundwater chemical evolution
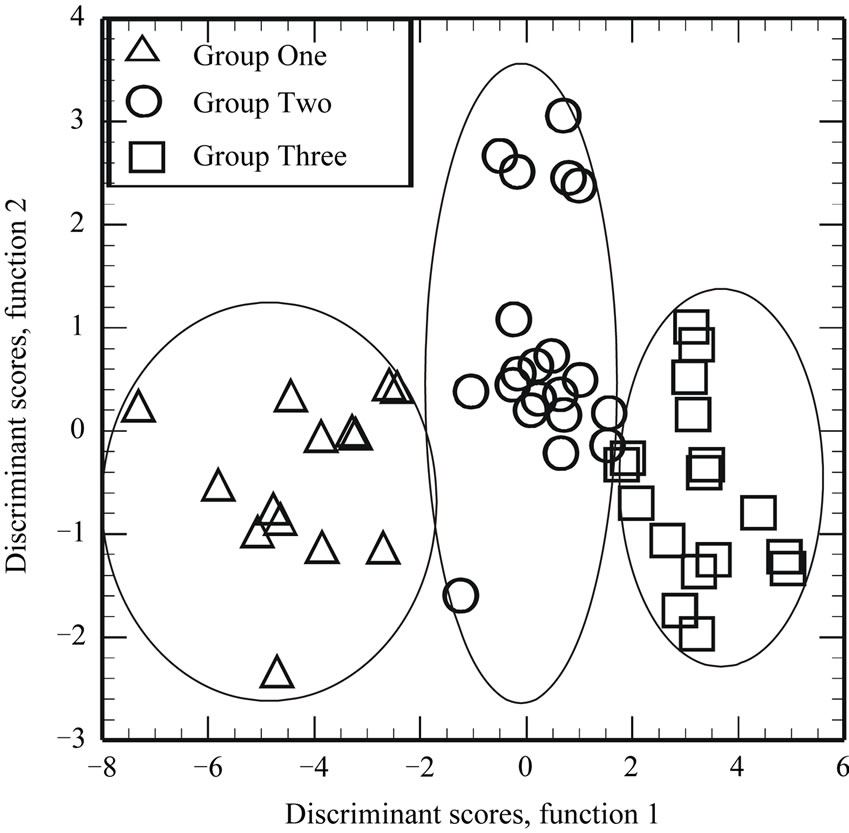
Figure 4. A plot of the first and second discriminant functions, showing groupings of the groundwater samples in the study area.
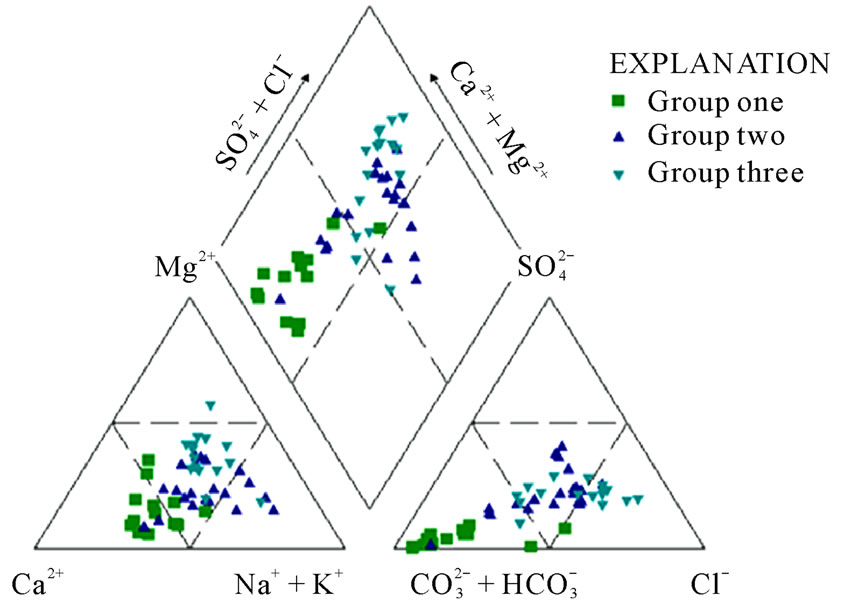
Figure 5. Piper plot of chemical data of groundwater samples in the study area.

Figure 6. Regression line between Oxygen-18 and deuterium for the LMWL, GWML and groundwater.
model [44-46], this type is regarded as recharged water in areas where groundwater is at its early stage of geochemical evolution. This may imply that the rapidly circulating groundwater has not undergone pronounced mineral-water interactions. Groundwater from the recharge area is characterised by Mg2+/Ca2+ ratio less than one, and is in favour of this argument. Groups two and three in the study area are derived from mixture of different water types ranging from Ca/Na-Cl, Ca/Na-HCO3, and Na-Cl; this may be due to fractures contributing water from different places which may not flow in a well defined flow lines. This process is likely in crystalline aquifer context such as the Densu region. As groundwater proceeds along the flow line, incongruent dissolution may continue whereby the impurities in the solid phase are progressively released and a purer mineral (in this case Mg2+) is produced.
Therefore, some of the groundwater samples will be characterized by Mg-HCO3 water type. Most of the groundwater samples in groups two and three (Figure 7) show Na/Ca-HCO3 water type, which may imply that the recharge waters might have undergone incongruent dissolution of silicate minerals, mainly plagioclase accompanied by cation exchange. The high TDS and the enrichment of Na+ ion along the flow line testify that the groundwater has undergone relatively pronounced degree of chemical evolution. Also, Mg2+/Ca2+ ratio greater than one for most of the groundwater samples in groups two and three confirm this process. This may imply long residence time of the groundwater samples in these groups.
3.5. Isotope Composition of Groundwater
The groundwater isotopic composition is an integrator of all recharge events; it will reflect the mixed isotopic signature roughly in proportion to the amount from flood recharge and “normal” recharge respectively [47,48]. The stable isotope contents appear fairly constant in time and they fingerprint the existence of different recharge episodes, if controlling factors such as temperature, humidity remain fairly stable. The isotopic content of groundwater in the study area ranges from –1.4% and –3.6% and –3.48% and –16.46% for δ18O and δD, with a mean isotopic composition of –2.8% and –11.16% for δ18O and δD respectively. A mean δ18O isotopic composition of –2.8% was obtained by [49] for groundwater in the Accra plains of Ghana, which forms part of the study area. This may imply that the shallow aquifer system in the study area have not undergone significant degree of fractionation.
A regression of the groundwater data show them to lie on a gradient of 5.8, which slightly deviates from the gradient of 7.7 obtained for the Local Meteoric Water Line. This certainly indicates that the infiltrated rainwater might have undergone some degree of fractionation both on land surface and in the unsaturated (vadose) zone before entering the groundwater reservoir (Figure 6). In Figure 7, it is observed that groundwater samples with high chloride contents are relatively enriched. The probable cause may be congruent dissolution of dry chloride deposits in the soil zone, or mixing with seawater intrusion since, δD and δ18O isotopic composition of seawater is zero. Similarly, in (Figure 8) there is a good correlation between δ18O content and  concentration in the groundwater samples. Few groundwater samples show elevated concentration of
concentration in the groundwater samples. Few groundwater samples show elevated concentration of 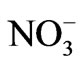 indicating anthropogenic point sources.
indicating anthropogenic point sources.
4. Conclusions
The Hierarchial Cluster Analysis (HCA) has classified the groundwaters of the study area into three groups. The advantage of the method was that the groups were objective, and clear geo-hydrological patterns were recognized. The subgroups show different degrees of water-rock interaction, residence time, as well as aquifer composition. The recharge zone, which is classified as group one samples are located in the northern portion of the basin. These aquifers are characterized by depleted δD and δ18O values with low TDS. The transmission and the discharge zones are characterized by relatively enriched δD and δ18O values, coupled with high TDS. This grouping was supported by the step-wise discriminant analysis (SDA) as 98% of the groundwater samples were grouped. The factor analysis also reveals that the variables were loaded fairly only in one component, thereby revealing a simple structure.
The dominant geochemical reactions in the basin are hydrolysis, incongruent dissolution, sulphate reduction as well as cation exchange. The recharge area is characterized by low TDS Ca-HCO3 → Ca-Mg-HCO3 water type to high TDS Na-HCO3→NaCl water type in the discharge area, which is typical of groundwater flow mechanism as in [50]. Additionally, different water types in
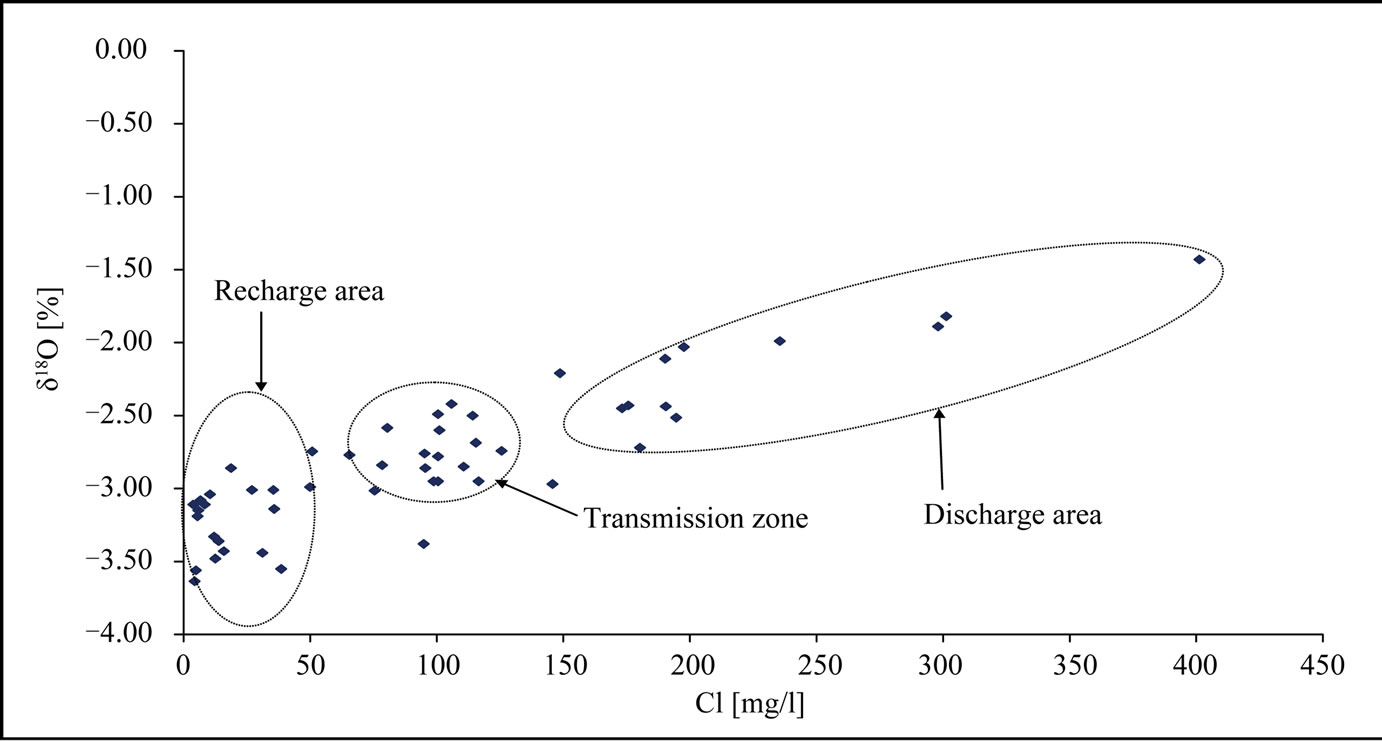
Figure 7. Scatter plot of oxygen-18 and chloride content of groundwater in the study area.
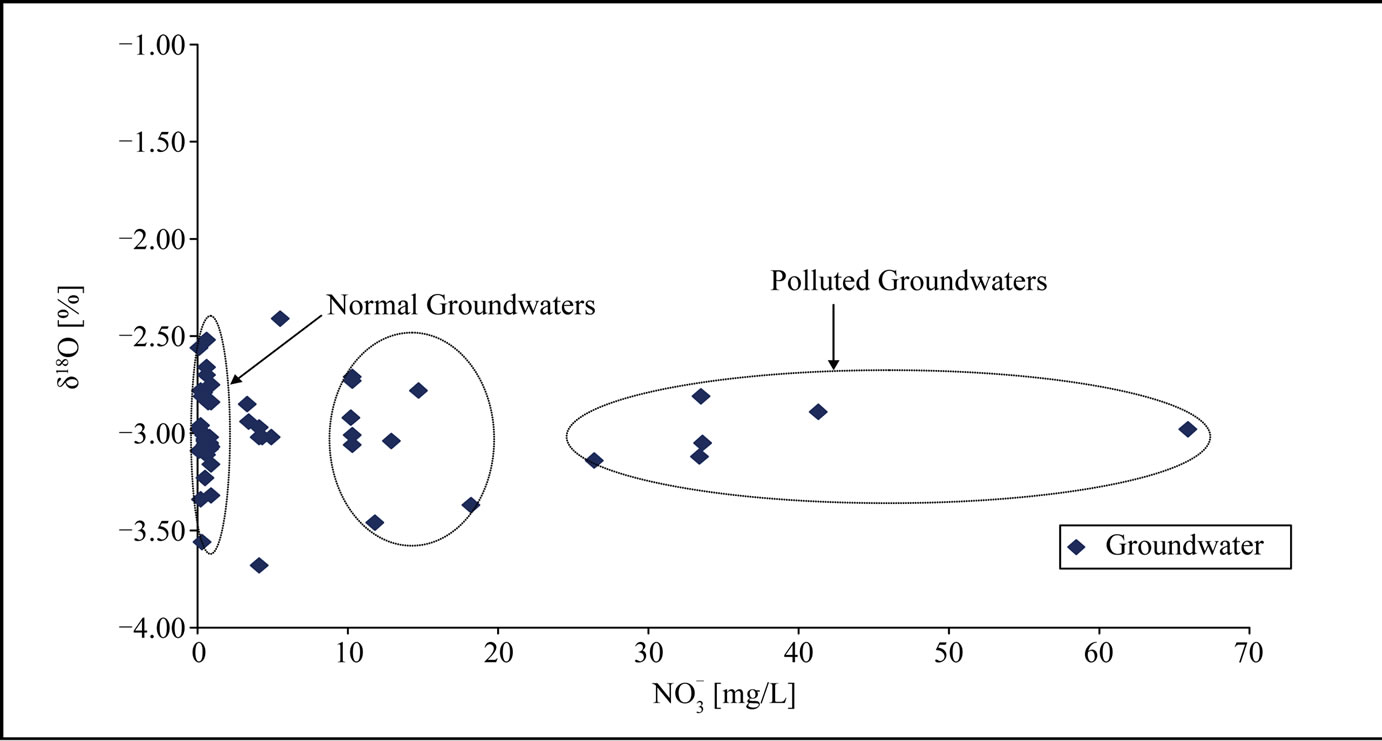
Figure 8. Scatter plot of oxygen-18 and nitrate content of groundwater in the study area.
the study area may be due to connected fractures in the weathered zone. Also, the Mg/Ca ratio in the groundwater samples increases along the flow line, as this may be used as an indicator of residence time and increasing maturity of groundwater. Generally, young groundwater will have low Mg concentrations as this was manifested in the groundwater samples in the study area. From the studies recharge to fractured aquifers by meteoric water may be through piston or preferential flow which has undergone some degree of fractionation. The aquifers seem to be connected as shown by the HCA and that the groundwater seems to flows from high topographic to lower topographic areas.
5. Acknowledgements
The authors are very grateful to the Director of National Nuclear Research Institute, Ghana Atomic Energy Commission and International Atomic Energy Agency for making funds available for this work. We also thank all the Technicians of the Chemistry Department, GAEC and Institute of Groundwater Ecology, Munich Germany for helping us during the sampling campaigns as well as the analysis.
REFERENCES
- Water Research Institute, “Borehole Yield Map of Ghana,” Water Research Institute, Accra, 1994.
- S. Dapaah-Siakwan and P. Gyau-Boakye, “Hydro-chemical Framework and Borehole Yields in Ghana,” Journal of Hydrology, Vol. 8, No. 4, 2000, pp. 845-852.
- N. S. Rao, “Seasonal Variation of Groundwater Quality in a Part of Guntur District, Andhra Pradesh,” Environmental Geology, Vol. 49, No. 3, 2006, pp. 413-429. doi:10.1007/s00254-005-0089-9
- T. Helstrup, N. O. Jørgensen and B. Banoeng-Yakubo, “Investigation of Hydrochemical Characteristics of Groundwater from the Cretaceous-Eocene Limestone Aquifer in Southern Ghana and Southern Togo Using Hierarchical Cluster Analysis,” Journal of Hydrology, Vol. 15, No. 5, 2007, pp. 977-989. doi:10.1007/s10040-007-0165-1
- W. M. Edmunds and P. Shand, “Groundwater Baseline Quality,” In: W. M. Edmunds and P. Shand, Eds., Natural Groundwater Quality, Blackwell Publishing Ltd., Malden, 2008, pp. 1-21.
- C. Kendal, J. J. McDonnell, “Isotope Tracers in Catchment Hydrology,” United State Geological Survey, Elsevier Science B.V., Amsterdam, 1998.
- K. Didane, L. Bouchaou, Y. Hsissou and M. Krimissa, “Hydrochemical and Isotopic Characteristics of Groundwater in the Souss Upstream Basin, Southwestern Morocco,” Journal of African Earth Sciences, Vol. 36, No. 4, 2003, pp. 315-327. doi:10.1016/S0899-5362(03)00050-2
- H. Suk and K. K. Lee, “Characterization of Hydrochemical System through Multivariate Analysis: Clustering into Zones,” Groundwater, Vol. 37, No. 3, 1999, pp. 358-366. doi:10.1111/j.1745-6584.1999.tb01112.x
- F. Sanchez-Martos, R. Jimenez-Espinosa and A. Pulido- -Bosch, “Mapping Groundwater Quality Variables Using PCA and Geostatistics: A Case Study of Bajo Andrax, Southeastern Spain,” Hydrological Science, Vol. 46, No. 2, 2001, pp. 227-242. doi:10.1080/02626660109492818
- M. Demile, S. Wohnlich, F. Wisotzky and B. Gizaw, “Groundwater Recharge, Flow and Hydrogeochemical Evolution in a Complex Volcanic Aquifer System, Central Ethiopia,” Hydrogeology Journal, Vol. 15, No. 6, 2007, pp.1169-1181. doi:10.1007/s10040-007-0163-3
- Y. Wang, T. Ma and Z. Luo, “Geostatistical and Geochemical Analysis of Surface Water Leakage into Groundwater on Regional Scale: A Case Study in the Liulin Karst System, Northwestern China,” Hydrogeology Journal, Vol. 246, No. 1-4, 2001, pp. 223-234.
- K. L. Locksey and M. E. Cox, “Statistical and Hydrochemical Methods to Compare Basalt and Basement Rock-Hosted Groundwaters: Atheron Tablelands, Northeastern Australia,” Environmental Geology, Vol. 43, No. 6, 2003, pp. 698-713.
- W. D. Alberto, D. M. del Pilar, A. M. Valeria, P. S. Fabiana, H. A. Cecilia and B. des los Angles, “Patterns Recognition Techniques for the Evaluation of Spatial and Temporal Variations in Water Quality, a Case Study: Suquia River Basin (Cordoba-Argentina),” Water Resources, Vol. 35, No. 12, 2001, pp. 2881-2894. doi:10.1016/S0043-1354(00)00592-3
- B. Helena, R. Pardo, M. Vega, E. Barrado, J. M. Fernandez and L. Fernandez, “Temporal Evolution of Groundwater Composition in an Alluvial Aquifer (Pissuerga River, Spain) by Principal Component Analysis,” Water Resources, Vol. 34, No. 3, 2000, pp. 807-816. doi:10.1016/S0043-1354(99)00225-0
- H. G. Pereira, S. Renca and J. Sataiva, “A Case Study on Geochemical Anomaly Identification through Principal Component Analysis Supplementary Projection,” Applied Geochemistry, Vol. 18, No. 1, 2003, pp. 37-44. doi:10.1016/S0883-2927(02)00099-9
- N. Consult, “Rapid Environmental Assessment and Action Planning of Densu River Basin in Ghana,” A Consulting Report, A United Nations Center for Human Settlements (Habitat) and Water Resources Commission of Ghana Funded, Accra, March 2001.
- K. B. Dickson and G. Benneh, “A New Geography of Ghana,” Longman Group UK Limited, Harlow, 1998, pp. 27-52.
- N. R. Junner, “Gold in the Gold Coast,” Gold Coast Geological Survey, Vol. 4, 1935, p. 67.
- N. R. Junner, “Geology of the Gold Coast and Western Togoland. Geological,” Survey Bulletin, Vol. 16, No. 11, 1940, pp. 5-10.
- A. Leube and W. Hirdes, “The Birimian Supergroup of Ghana—Depositional Environment, Structural Development and Conceptual Model of an Early Proterozoic Suite,” Federal Institute for Geosciences and Natural Resources, unpublished report 99529, Hanover, 1986, p. 260.
- H. E. Gill, “A Groundwater Reconnaissance of the Republic of Ghana, with a Description of Geo Hydrologic Provinces,” Geological Survey Water-Supply Paper 1757- -K, Washington, 1969.
- Water Research Institute, “Groundwater Resources Assessment of Ghana,” Water Research Institute/Council for Scientific and Industrial Research, Accra, 1999.
- P. K. Darko and J. Krásný, “Regional Transmissivity Distribution and Groundwater Potential in Hard Rocks of Ghana,” In: J. Krásný, Z. Hrkal and J. Bruthans, Eds., Groundwater in Fractured Rocks, Taylor & Francis, Boca Raton, 2003, pp. 45-46.
- P. G. Cook, “A Guide to Regional Groundwater Flow in Fractured Rock Aquifers,” Seaview Press, Henley Beach, 2003.
- Water Resources Research Institute, “Groundwater Assessment: An element of integral Water Resources Management-The Case of the Densu River Basin,” 2003.
- R. A. Freeze and J. A. Cherry, “Groundwater,” Prentice Hall, Englewood Cliffs, 1979.
- S. Epstein and T. K. Mayeda, “Variations of 18O Content of Waters from Natural Sources,” Geochimica et Cosmochimica Acta, Vol. 4, No. 5, 1953, pp. 213-224. doi:10.1016/0016-7037(53)90051-9
- M. L. Coleman, T. J. Shepherd, J. J. Durham, J. E. Rouse and G. R. Moore, “Reduction of Water with Zinc for Hydrogen Isotope Analysis,” Analytical Chemistry, Vol. 54, No. 6, 1982, pp. 993-995. doi:10.1021/ac00243a035
- T. B. Coplen, “Normalization of Oxygen and Hydrogen Isotope Data,” Chemical Geology, Vol. 72, 1988, pp. 293-297.
- C. Güler, G. D. Thyne, E. J. McCray and A. K. Turner, “Evaluation of Graphical and Multivariate Statistical Methods for Classification of Water Chemistry Data,” Hydrogeology Journal, Vol. 10, No. 4, 2002, pp. 455-474. doi:10.1007/s10040-002-0196-6
- C. E. Brown, “Applied Multivariate Statistics in Geohydrology and Related Sciences,” Springer, Berlin, 1998, p. 248.
- J. H. Ward, “Hierarchical Groupings to Optimize an Objective Function,” Journal of American Statistical Association, Vol 58, No. 301, 1963, pp. 236-244.
- B. A. Helena, M. Vega, E. Barrado, R. Pardo and L. Fernandez, “A Case of Hydrochemical Characterization of Alluvial Aquifer Influenced by Human Activities,” Water Air and Soil Pollution, Vol. 112, No. 3-4, 1999, pp. 365-387.
- R. P. Ashley and J. W. Lloyd, “An Example of the Use of Factor Analysis and Cluster Analysis in Groundwater Chemistry Interpretation,” Journal of Hydrology, Vol. 39, No. 3-4, 1978, pp. 335-364.
- S. X. Meng and J. B. Maynard, “Use of Statistical Analysis to Formulate Conceptual Models of Geochemical Behavior: Water Chemical Data from the Botucatu Aquifer in São Paulo State, Brazil,” Journal of Hydrology, Vol. 250, No. 1-4, 2001, pp. 78-97.
- R. E. Williams, “Statistical Identification of Hydraulic Connections between the Surface of a Mountain and Internal Mineralized Sources,” Ground Water, Vol. 20, No. 4, 1982, pp. 466-478. doi:10.1111/j.1745-6584.1982.tb02767.x
- J.-H. Kim, R.-H. Kim, J. Lee, T.-J. Cheong, B.-W. Yum and H.-W. Chang, “Multivariate Ststistical Analysis to Identify the Major Factors Governing Groundwater Quality in the Coastal Area of Kimje, South Korea,” Hydrological Sciences, Vol. 19, No. 6, 2005, pp. 1261- 1276. doi:10.1002/hyp.5565
- C. Güler and G. D. Thyne “Hydrologic and Geologic Factors Controlling Surface and Groundwater Chemistry in Indian Wells-Owens Valley Area, Southern California, USA,” Journal of Hydrology, Vol. 285, No. 1-4, 2004, pp. 177-198.
- R. A. Johnson and D. W. Wichern, “Applied Multivariate Statistical Analysis,” 3rd Edition, Prentice-Hall Inc., Englewood Cliffs, 1992.
- O. Vaseli, A. Buccianti, C. De Siena, N. Coradossi and M. Angelone, “Geochemical Characterisation of Ophiolitic Soils in a Temperate Climate; a Multivariate Statistical Approach,” Geoderma, Vol. 75, No. 1-2, 1997, pp. 117- 123.
- S. Swanson, J. Bahr, M. Schwar and K. Potter, “Two- -Way Cluster Analysis of Geochemical Data to Constrain Spring Source Waters,” Chemical Geology, Vol. 179, No. 1-4, 2001, pp. 73-91.
- J. Taboada, A. Vaamonle, A. Saavedra and L. Alejano, “Application of Geostatistical Techniques to Exploitation Planning in Slate Quarries,” Engineering Geology, Vol. 47, No. 3, 1997, pp. 269-277. doi:10.1016/S0013-7952(97)00024-0
- H. F. Kaiser, “An Index of Functional Simplicity,” Psychometrika, Vol. 39, No. 1, 1974, pp. 31-36.
- L. Plummer, J. Busby, R. Lee and B. Hanshaw, “Geochemical Modeling of the Madison Aquifer in Parts of Montana, Wyoming, and South Dakota,” Water Resource Research, Vol. 26, No. 9, 1990, pp. 1981-2014.
- W. M. Edmunds and P. Smedley, “Residence Time Indicators in Groundwater: The East Midlands Triassic Sandstone Aquifer,” Applied Geochemistry, Vol. 15, No. 6, 2000, pp. 737-752. doi:10.1016/j.jhydrol.2003.08.019
- S. Adams, G. Tredoux, C. Harris, R. Titus and K. Pietersen, “Hydrochemical Characteristics of Aquifers near Sutherland in the Western Karoo, South Africa,” Journal of Hydrology, Vol. 241, No. 1-2, 2001, pp. 91-103.
- A. L. Herczeg and T. E. Payne, “Recharge and Weathering Processes in Fractured Rock Aquifers in Northern Australia,” In: Y. Kharaka and A. E. Maest, Eds., Water-Rock Interaction, Balkema, Rotterdam, 1992, pp. 561-564.
- T. Coplen, A. L. Herczeg and C. Barnes, “Isotope Engineering-Using Stable Isotopes of the Water Molecule to Solve Practical Problems,” In: P.G. Cook and A. L. Herczeg, Eds., Environmental Tracers in Subsurface Hydrology, Kluwer Academic Pubs, Boston, 2000, pp. 79-110.
- T. T. Akiti, “Geochemical and Isotopic Studies of Groundwater in Upper West Region of Ghana,” Unpublished Ph.D. Thesis, Universitié de Paris Sud, Paris, 1980.
- I. I. Chebotarev, “Metamorphism of Neutral Water in the Crust of Weathering,” Geochemica et Cosmochimica Acta, Vol. 8, 1955, pp. 22-48, 137-170, 192-212.

