Journal of Service Science and Management
Vol.08 No.01(2015), Article ID:53855,6 pages
10.4236/jssm.2015.81010
Discourse about Linear Programming and Lean Manufacturing: Two Different Approaches with a Similar, Converging Rational*
Bruno G. Rüttimann
Inspire AG/ETH Zurich, Zurich, Switzerland
Email: brunoruettimann@bluewin.ch, ruettimannbrunog@ethz.ch
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 19 January 2015; accepted 3 February 2015; published 6 February 2015
ABSTRACT
In recent years, the Toyota Production System has also assumed in western manufacturing plants a predominant position. Lean Manufacturing, as it is usually called in the occidental world, aims at a “Single-piece-flow” job handling and has its advantages compared to the classic “Batch and Queue” job handling. On the other hand, mathematical Linear Programming optimization techniques have passed into oblivion, having obtained the feel to be inappropriate for production planning. Although the two approaches have different aims and application, they give particular attention to scarce resources. The concepts of “bottleneck” in Lean Manufacturing and “shadow price” in Linear Programming are complementary. The paper shows the different focus of the two approaches and crystallizes their synergic values.
Keywords:
Linear Programming, Lean Manufacturing, Shadow Price, Bottleneck

1. Introduction
In the seventies and eighties Operations Research (OR), the branch of mathematics dealing with optimization problems, became very popular. Within the multiple classes of problems, especially those problems characterized by one objective in a deterministic environment and linear equations, solvable with Linear Programming (LP) and its Simplex algorithm, it found selective application in industry. Increasing computational power helped to spread the technique into the offices of multinational enterprises. But it encountered the same destiny
as cybernetics in the sixties―it lost attractiveness. In fact, lack of realistic practicability prevailed over the illusion of being able to optimize socio-economic systems with the computer. Since the nineties, after the spreading of the Toyota Production System (TPS) in America and Europe, which became popular with the name of Lean Manufacturing (LM), production has put the emphasis rather on cost savings and waste reduction (Muda) and continuous improvement (Kaizen) than on overall margin optimization. Indeed, modern production planning systems have other, more practical optimization functions than the valid but theoretical maximizing margin contribution approach. In fact, the production mix cannot always be changed in the short term and is usually given by the customer base, especially if production is “made to order”. LP suffered the reputation of being too academic, although the basic concepts retain its validity and have its proven field of application, such as e.g. in transportation. Nevertheless, LP optimization of production and LM organization of work put the same attention to scarce resources of production, resources becoming the “bottleneck” of production, which makes it worth to compare the two approaches. In the following, we will analyze the peculiarities of each approach and show the dichotomic characteristics of both optimization techniques.
2. Linear Programming Aiming at Overall Optimization
What is the classic problem statement of an LP optimization problem for a plant manager? Given is a manufacturing plant with m machines, with each machine having a capacity of bm. With these machines, n products with the quantity xn are manufactured. The specific occupancy load of the m resources with the n products is given by the matrix A of dimension [mn]. Every product generates its specific margin contribution cn. The aim is to identify the optimal product mix x*, i.e. the quantity of each single product to be produced, which maximizes the overall margin contribution complying with the resource restrictions. The problem solved by LP is often also called “Linear Optimization”. The problem can be written in mathematical terms represented by the standard form
 (1)
(1)
where the restrictions, given by the machine capacities, have been added with the non-negativity requirements of production volume of the optimization variables xn. The resulting overall margin contribution of the maximizing function z is a scalar product, given by the transposed vector cT of specific margin contribution coefficients and the vector of the product mix x. The mathematical problem has also a geometric interpretation as represented in Figure 1 showing the plane geometry case of two products and three machines.
LP is a special case of convex optimization which can be solved via the Simplex algorithm presented first by Dantzig, a numeric solving technique well explained in scholastic literature, which we will not deal with here. The number of basic solutions are
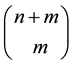 (2)
(2)
The number of feasible basic solutions, which is smaller than calculated by (2), are given by the domain of definition, represented through the polyhedron delimited by the intersecting linear restrictions, i.e. the straight lines g1, g2, g3, and the two x-axes. The number of feasible basic solutions of the Simplex algorithm are given by the corners of the convex polygon of which one is the optimal basic solution x* maximizing the objective function. To solve the system of linear equations, slack variables ym are introduced to transform inequality restrictions into easy solvable equations.
Each primal problem has associated a dual problem (3), where capacities are switched with the coefficients of the objective function; the primal slack variables become the optimizing variables of the dual LP problem.
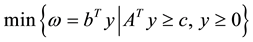 (3)
(3)
In the case of n < m it may be useful to solve the dual problem of the slack variables instead of the primal problem to shorten the number of iterations, given the fact that the primal solution can also be seen in the dual Simplex table. The interpretation of the slack variables in a production problem of LP is unused resource, i.e. spare production capacity of the resource where the slack variables have a positive value other than zero. This represents the “shadow price” of the resource in the dual problem. If a slack variable is zero, the shadow price of this resource is zero. In economics the shadow price corresponds to the opportunity cost of the alternative use of the resource, i.e. selling the resource instead of using it for production.
Figure 1. Geometric solution to an LP problem with two products x1 and x2.
Key questions of LP are related to sensitivity and post-optimality. Sensitivity is the analysis of the effects on the objective function z by varying the input parameters Amn, bm, and cn (4). Geometrically interpreted, changing the bm corresponds to shifting parallel the straight line of the resources, whereas changing the cn corresponds to change the slope of the objective function.
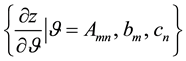 (4)
(4)
Post-optimality (5) analyses the stability of the optimal basic solution x*, i.e. within which interval Δθ the input variables can vary without changing the validity, i.e. the composition of the optimal basic solution.
 (5)
(5)
This represents, without going into detail, some questions related to LP problems in a production environment. This simplified formulation of LP problems does not take explicitly into consideration, e.g., size of production batches or the problem of change-over, complications which can approximately be solved by reducing the capacity of the resources bm or more exact by passing to another class of optimization problems, being solvable with general Mathematical Programming.
In the case of non-linear problems, an objective function expanded by the restrictions with Lagrange multiplier can be used. For concomitant application of multi objective functions, Pareto optimality is applied. A multi- objective solution is said to be Pareto efficient when any change of improvement for one objective function is done to the detriment of another objective function.
3. Lean Manufacturing Aiming at Local Optimization
Let us have a look at what is the LM problem statement for a plant manager. Given is the situation that several customers require the even supply over time (i.e. a constant supply rate) of different products of a certain quantity per year, resulting in a given takt rate (TR). Apart of the elimination of waste (Muda) in the process and the continuous improvement philosophy, the aim of LM is to implement a customer-pull takted single-piece-flow (SPF) what we can synthesize with formula (6) and to satisfy the on-time-delivery (OTD) to customers. This is called a just-in-time (JIT) production. Thereby it does not matter if production is “made to stock” (more suitable for standard products) or “made to order” (more applicable for customized products). We can define JIT mathematically as
 (6)
(6)
i.e. a pull-production, where handled quantities n tend to one (single-piece-flow). Please note, that the SPF applies to the handled quantity, not necessarily to the size of the production batch, which has also to match with technical restrictions. JIT means producing and supplying the right material, in the right quantity, at the right time, to the right place. A lean-optimized production cell represents JIT in its perfection.
To implement JIT production, manufacturing cells are conceived. Instead of grouping similar technologies into the same workshop according to western production philosophy, the necessary equipment and machines to manufacture similar products are displayed in-line into a U-shaped production cell; in this discourse we will use the term manufacturing and production indifferently. The manufacturing cell is a product-optimized transfer-line fabrication, with all necessary resources. If a cell is dedicated to one product we talk about mono product cell, otherwise mixed product cell. A cell is characterized either by its cycle time (CT) at the bottleneck (or the workstation turnover time WTT of the bottleneck in a mixed product cell), or its inverse value which is the throughput, also called exit rate (ER) or completion rate, where CT should not be confused with the process lead time (PLT) of the whole cell.
A customer-pull takted SPF requires that all cycle times CTij of the operations i in a cell j are equal (no Mura), this is called a “balanced line”, i.e.
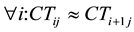 (7)
(7)
whereas the cycle times of different cells j and k may differ
 (8)
(8)
The necessity may exist to link different cells. When the cells have different cycle times (8), Kanban supermarkets are interposed between cells to decouple the cells. This allows the different cells to optimize their production without being influenced by other cell scheduling, each cell becomes a self-controlled production unit.
Within LM, theory of constraints (TOC) represents a central focus in cell-design. Restriction in production capacity of a cell, or more generally of a production plant, is given by the throughput, i.e. the exit rate ER of the considered manufacturing unit. The operation with the lowest ER (9) is the bottleneck of the production line.
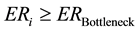 (9)
(9)
Therefore, in LM most attention is put on the bottleneck, because this limits directly the profitability of the production unit. Within the JIT philosophy the bottleneck receives an additional aspect: it also usually represents the controlling element of the cell, the “drum” complying with the production takt required by the customer’s takt rate (TR). Indeed, it has to result
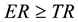 (10)
(10)
i.e., the ER of the cell has to be bigger than the TR required by the customer, otherwise the cell would not be able to satisfy customer’s demand. The inverse value of the TR is takt time (TT) and (10) becomes
 (11)
(11)
The dimension of time (11) in cell-design is usually preferred over the dimension throughput (10), because to balance each operation of a cell (7), the work content is usually expressed in time units (seconds or minutes) and will be used to optimize the work distribution within the cell. When performing a TOC analysis, a Time-Opera- tion chart as represented in Figure 2 is a suitable tool to reveal visually process steps with cycle times that are longer than takt time; these operations are called constraints. The process step with the longest cycle time is the bottleneck. Please note, there may exist several constraints but every process has only one bottleneck.
To conclude, in the LM approach the triggering of the production at the “drum” of the line is done by downstream customer’s Kanban. To guarantee the perfect operation of the manufacturing line, the “Drum-Buffer- Rope” technique is usually used, i.e. the drum has always to work assured by a full buffer and the upstream operations are triggered by the “rope” via Kanban.
Figure 2. Time-operation chart of a manufacturing cell.
4. Synthesis of Both Approaches
As we notice, the problem statements in the cases of LP and LM are slightly different. For LP: given scarce resources to produce products, what would be the optimal product mix to maximize the margin contribution objective function; this represents a problem aiming at maximizing effectiveness of transformation in a production plant. For LM: given a product mix, how to manufacture it in an optimal way; this represents a problem aiming at maximizing efficiency of transformation. After having exposed both approaches, let us elucidate the following emerging insights:
First: LP starts from the available resources bm, usually expressed in time units, and asks what can be produced x* to maximize a target function z such as (1), typically an economics (theoretic) approach of overall optimization. LM starts from a given mix x and asks how to produce it efficiently, a question of coefficient matrix A, i.e. [amn], expressed in time per piece, typically a production (practical) approach of local optimization.

In other words: LP maximizes a single objective function z considering several restrictions regarding resources bm and tries to identify the optimal product mix x*, which maximizes the target function. LM tries to satisfy several customer requirements, such as takt rate TR and expected delivery time EDT, i.e. the mix is given, and tries to optimize the parameters of a multi objective equation system (12), which allows JIT supply. Nevertheless, both are problems of solution existence.
Second: In the LP problem, the bottleneck is given by the resource with the lowest residual machine capacity bm with the optimal mix; the resources are expressed e.g. in hours or days, which is an aggregated figure. In LM the bottleneck is defined by the largest coefficient amn of the matrix A, a specific value, e.g. minutes/piece (13).

In other words: Both problem statements are restricted in the short term by scarce resources, but the scarce resource is interpreted slightly differently in the LP and the LM problems. Bottleneck in LP means an active restriction of bm in Ax ≤ b, whereas bottleneck in LM means the operation with the longest cycle time amn of the non-balanced matrix A. In addition, in a mono product cell, the bottleneck is identical (14); this is not necessarily the case in mixed product cells (15). Nevertheless, this shows the converging rational of both approaches at the optimum, i.e. of the overall production system or locally in the manufacturing cell.
Third: In the LP problem, the resources bm are aimed to be fully utilized, corresponding to minimize the slack variables ym ideally becoming zero. In LM the manufacturing cell is optimized, in order to get a cycle time-ba- lanced amn column of the matrix to comply with a JIT supply to the customer’s required takt time (12); according to (7), in a mixed product cell all the columns have to be linearly dependent (16).
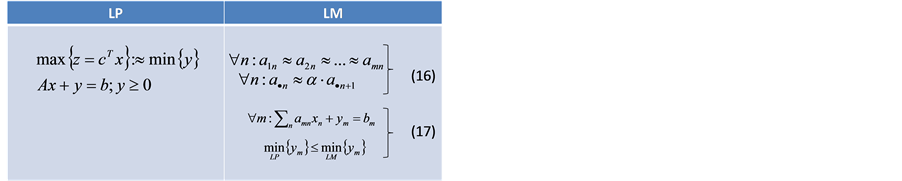
In other words: In LM the resource utilization is of second priority and does not appear in (16); it can even be increased deliberately to a certain extent if the need arises. It can happen, that the artificial summation of the resource utilization of different cells in a multi cell plant, may not have an optimal resource bm utilization, i.e. in this case the slack variables ym are greater than in an overall optimized LP problem (17). In fact, a JIT SPF cell- design may result in less capacity because each of the capacities bm have been split into the different cells.
Forth: In an LP problem, batch size is not investigated and does not appear in the problem and restriction statement (12). In LM, batch size is of fundamental importance to comply with (12); flexibility (and quick changeovers) is mandatory for a mixed product cell.
In other words: In LP the products of the mix xn may be produced in n big batches (one for each xn) or could be produced in several batches for each product xn according to the economic batch quantity Bopt; this corresponds to a clear push manufacturing philosophy without dedicated resources. In LM the optimal batch size gives maximum flexibility of a mixed product cell to allow the production of several products within the same cell, even to be produced several times a day, leveled according to pitch scheduling of a Heijunka box. Lean batch sizing optimizes the batch Bi considering workstation turnover time WTT and desired takt rate of the customer to be produced ideally in a JIT SPF cell-design (18).
Fifth: In LP the focus of optimization is driven, for economic reason, to the objective function with priority given rather to sensitivity than to post-optimality. In LM the focus is put on balancing the operations of the workstations composing a cell (16); this is a problem of post-optimality.
In other words: LP addresses mainly the question of how much will the objective function be improved by infinitesimal change of the parameter, i.e. for example, changing the bottleneck resource bm by a marginal unit, reflecting the “shadow price” of the resource. LM addresses mainly the balancing of the cell to allow JIT supply according to customer’s TR; the aim is to determine the balanced [amn] with less waste, i.e. minimize Muda within the process (19).
Final consideration: The above considerations show, that the problem statement is different, although the problem structure appears to be similar. The question is therefore not do we apply LP or LM; they solve different problems. Indeed, we can state, LP deals “ex-ante” to determine the overall maximum, which concept is suitable for sales managers dealing with effectiveness of resource transformation. The LM approach deals “ex- post” to optimize the given mix, i.e. having the production mix fixed, in order to determine the local maximum (efficiency of resource transformation), this concept is suitable for production managers. Mathematically interpreted, LM can be assimilated to the method of the gradient leading to find local optima and the Kaizen to the step of the steepest ascent. LP through the iteration within a convex space delivers the overall maximum of the whole production system; LM may not be of convex programming but through the Kaizen iteration it approaches the overall maximum without ever reaching it. This shows that Lean is not only a toolset but primarily a management philosophy of continuous improvement.
5. Conclusion
Both approaches have the same rational to focus on the bottleneck of production to increase the output function. But at the end, LP has more the feel of an intellectual exercise rather than of being of great practical help to manage a production system. Indeed, the mix is usually already outlined by strategy, LP-optimized or not, and then given in reality by the sales department’s activity. Therefore the question interesting the production manager is not what would be the ideal mix, but rather how to deliver in time without quality issues to the customers with the actual mix. This shows, LM is more a day by day business approach in search of excellence, helping to satisfy, in a cost efficient way, changing customer needs. That relegates LP applied to manufacturing problems to a minor role. In other applications, such as transportation problems to optimize complex routing, LP may keep its reason to exist also in day to day business. In a nutshell, in production problems, LP and LM deal with different objectives. Nevertheless, LP has its reason to exist in the sales and marketing department to address and leverage equipment-optimized products. In the sales department considerations of price elasticity may help to force the load-optimized mix of the plant; for that LP is the ideal tool. As we can see, the two approaches are not mutually exclusive, they are more synergically complementary.
References
- Rüttimann, B. and Wegener, K. (2014) Introduction to Lean Production and Six Sigma Quality Management, ETH Tools IV course, HS 2014 Lecturing Notes.
NOTES
*This paper is based on reference [1] .






