Journal of Biomedical Science and Engineering
Vol.6 No.8(2013), Article ID:35655,7 pages DOI:10.4236/jbise.2013.68103
Chaotic approach in biomedicine: Individualized medical treatment*
![]()
Institute of Techniques and Natural Sciences, Surgut State University, Surgut, Russia
Email: valery.eskov@gmail.com
Copyright © 2013 Valery M. Eskov et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received 16 May 2013; revised 17 June 2013; accepted 1 July 2013
Keywords: Personification; Phase Space; State Vector; Attractor; Complexity; Chaos; Self-Organization; Medicine
ABSTRACT
According to classic deterministic-stochastic approaches, we don’t have any possibility for realization of the basic principle in medicine because every human organism has its own specific features. It is evident for us that requirement of medical personification includes two procedures: individual (with uninterrupted procedure of human organism state measurement) diagnostics and the second part which is connected with uninterrupted control of the efficiency of medical treatment and measurements of human organism parameters. We conduct the diagnostics according to behavior of state vector of human organism in phase space of states according to every coordinates of human’s state vector and with calculation of quasiattractors. We can present the results of our observations: what may be good for one person is not necessarily good for another. We present new bioinformational methods and software for calculation of quasiattractors parameters for dissolving such contradictions between deterministic-stochastic medicine and the use of theory of chaos self-organization where the state vector of human organism demonstrates uninterrupted movements. The practical results of such procedure are also presented according to the theory of chaos-self-organization. So there are great distinctions between the classic deterministic-stochastic approach (based on traditional medicine requirements) and the new theory of chaos self-organization which considers every human organism as a unique system with individual properties.
1. INTRODUCTION
Biomedical systems are distinguished by complex dynamics in which the components of the system’s state vector (SSV) along with their internal control and adjustment systems constantly vary, thereby maintaining, for example, homeostasis. Such third-type systems constantly vary within certain volumes of the phase space of states (they will be referred to as quasi-attractors).
The present study discusses typical examples from biomechanics and medicine that illustrate these laws and represent essentially new capabilities for the study of complex biosystems from the standpoint of multidimensional phase spaces and the theory of microchaos (theory of chaos—self-organization—TCS).
In order to describe, model, and predict especially complexly organized biosystems, objects, phenomena, and processes must be repeatable or reproducible without limit. In Nature, however, there exist a vast number of objects that do not exhibit fully determined laws of development and functioning within the framework of a nonuniform distribution (systems of the third type). In this case, such objects and the state vector of the particular system possess certain bounded regions in the phase space of states, i.e., numerical constraints on the movement dynamics of the state vector of the system in the phase space of states (PSS). The variations in the parameters of a system within these regions are chaotic in nature.
The quasi-attractors themselves continuously shift in this phase space [1-3]. The latter circumstance entirely precludes the repetition or reproducibility of any mathematically recorded state of biological dynamic systems, since their parameters simultaneously “flicker” and “float” in the phase space of states. In other words, both the state vector of the system and the quasi-attractors themselves may vary and shift in the phase space of states. So, quasi-attractors may be presented as individual state of one individual or a group of patients with their specific parameters of body state.
It is impossible to describe such systems within the framework of traditional deterministic and stochastic approaches, and extremely difficult to do so within the framework of chaos theory and the theory of self-organization (the chaos—self-organization). Below, we will propose a change from measurements and modeling of complex biosystems from the standpoint of deterministic and stochastic approaches to the field of TCS.
2. FEATURES OF BIOMEDICAL SYSTEMS
Without dwelling in detail on all the features of “human-scale systems” and in particular “biosystems”, about which we have already written many times [1,2], let us briefly note five basic properties of biomedical dynamical systems, the understanding of which is of fundamental importance for developing new concepts for studying them and building behavioral models. These properties significantly distinguish biomedical dynamical systems from other systems studied in physics, chemistry, or engineering. Let us list them:
1) Property of compartmental-cluster organization— CCO. Biological dynamical systems are systems with a compartmental and cluster structure, where the individual (arbitrary!) unit (the compartment) can consist of a single element or a whole set, but in this case the behavioral dynamics of such a set (compartment or cluster (an ensemble of compartments)) is important. The cluster structure of biomedical systems requires new measurement methods and models. In this case, it is obvious that such cluster biological dynamical systems are complex hierarchical systems, and they have to be described by multicomponent vectors 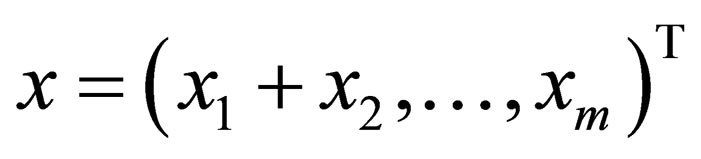 in an mdimensional phase space of states. Some theories are already available today for such biological dynamical systems, one of which we have presented many times over the past 20 years [4-6].
in an mdimensional phase space of states. Some theories are already available today for such biological dynamical systems, one of which we have presented many times over the past 20 years [4-6].
2) Glimmering property. A very difficult feature of biological dynamical systems is the constant variation in the structure and relations, i.e., these systems are “glimmering systems”. And this “glimmering” involves changes not only in the parameters of the system state vector but also in the dimensionality of the phase space of states, in the meaning of xi (for example, now these xi are the order parameters, but a little later they are no longer the order parameters and other quantities have taken over). It is very complicated to work with such “glimmering systems”; there are no analogs for them in physics or chemistry, since the term “fluctuations” has an already established meaning in the exact sciences and can only be used quite arbitrarily for such systems [1,2,7].
3) Evolution property. Such complex “glimmering” biological dynamical systems have the property of evolving. Consider the microevolution of a human (as an example of one of three systems in the phase space of states, from birth to old age and death) or the evolution of humanity (transition from a traditionalist to a technological society and then to a knowledge-based, synergistic, post-industrial society). Micro-evolution or macroevolution is inherent to any biological (medical) dynamical system, and this represents yet another complication (in predicting both the dynamics and the final state of this evolution).
4) Teleological property. All biological (medical) dynamical systems also have the property of teleology. Possibly this concept should include another meaning than intended by L. von Bertalanffy, but there is some final goal in the developmental dynamics of any system. For example, for a human, this is the process of accumulation of information for himself or herself and for humanity (if this human is a scientist) or the inevitability of death for a human, and perhaps also for all of humanity (!?). All this still needs to be studied, but these properties clearly appear in the dynamics of any medical dynamical system (in particular, for the functional systems of the body).
5) Exceeding the three sigma limits. The most “extravagant” property of biological dynamical systems, and the one that weighs most heavily on proponents of the deterministic/stochastic approach, is the property of exceeding the three-sigma limits (for a gaussian distribution, the probability of falling outside these limits is P < 0.003). In principle, for biological dynamical systems, all evolution of the living occurs beyond the three-sigma limit, i.e., there are huge “biofluctuations”, deviations from the average values.
It is evident for us there are some special third type of systems (TTS) which have five special properties (see above) and 13 distinguishes from ordinary deterministic and stochastic systems [7,8] and all medical systems (especially all functional systems of human organism— FSHO) which provide the homeostasis in normal or pathological state of human organism.
3. ALGORITHM AND SOME PROBLEMS OF ITS APPLICATIONS IN MEDICINE
Algorithm for calculating the parameters of quasi-attractors for the human state vector is based on calculation of SSV parameters. The data obtained from one or a group of test subjects by repetitions of the measurements in the form of a set m of data blocks (compartments) where m is the number of measured biological indices, are transferred in the form of points to an m-dimensional phase space of states, in which, fixing the extreme left-hand and right-hand values of the parameters for the human state vector along each coordinate xi, they generate a quasi-attractor in the form of an m-dimensional parallelepiped, for which we determine the volume Vg, the center, and the asymmetry value. Using these three quantities (absolute or relative), we decide if the recovery is effective by comparing these parameters before and after treatment. Essentially, each group of test subjects forms a certain “cloud” in the phase space of states, which has its own limits Dxi along each of the coordinates xi (i=1,2,..., m). These limits Dxi are the faces of the m-dimensional parallelepiped in the m-dimensional phase space, and each face represents the level of variability of the i-th parameter (diagnostic index), a component of the vector x in the phase space of states.
The total volume of this parallelepiped is the volume Vg of some quasi-attractor, which for different groups of test subjects has its own parameters before and after treatment. These parameters include: the volume of the quasi-attractor Vg, the coordinates of its center C in the phase space of states, the asymmetry r. We determine either the absolute values (DVg = Vg2 − Vg1, where Vg2 are the values of Vg after treatment, and Vg1 are the values before treatment) or the relative values in percent (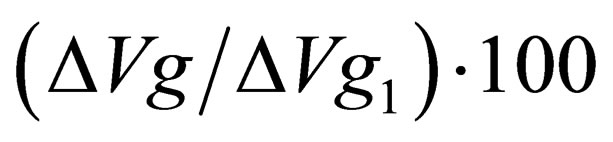 ) of these parameters. If the relative changes in the parameters of the quasi-attractor exceed the uncertainty in the measurement of the diagnostic indices, then they are already considered significant (in many cases, they are 5% or 10% or more). The larger the changes in these three overall (integrated) indices, the more effective is the recovery.
) of these parameters. If the relative changes in the parameters of the quasi-attractor exceed the uncertainty in the measurement of the diagnostic indices, then they are already considered significant (in many cases, they are 5% or 10% or more). The larger the changes in these three overall (integrated) indices, the more effective is the recovery.
At the suggestions of a number of researchers, a period of review of the laws of the deterministic-stochastic approach has begun in biology and medicine, and other methods of measurement, calculation, and description of complex medico-biological processes and objects from the standpoint of chaos and self-organization theory are needed. In this case, it has been suggested that quasi-attractors should be used (as kinds of “clouds” in a phase space of states) and that their parameters (volumes, coordinates of the center, intra-attractor distances, etc.) be calculated. Other representations and laws arise within the framework of such an approach. For example, biological dynamical systems (BDS) do not possess stationary regimes and states and there are no stationary points, i.e., 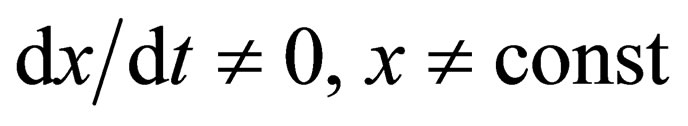 , since the state vector of a system is continuously and constantly “flickering” within certain quasi-attractors in a phase space of states. The models that already exist for the description of biological dynamical systems constitute only a single copy of the physical world. This question is considered in greater detail in [9], and the present article represents a further development of methods for the measurement of biological dynamical systems that have already been introduced.
, since the state vector of a system is continuously and constantly “flickering” within certain quasi-attractors in a phase space of states. The models that already exist for the description of biological dynamical systems constitute only a single copy of the physical world. This question is considered in greater detail in [9], and the present article represents a further development of methods for the measurement of biological dynamical systems that have already been introduced.
At the same time, model equations based on physical data describe the trajectory of the movement not of individual elements of a system (as in deterministic and stochastic approaches) or the motion trajectories of the state vector of a system, but instead the coordinates of the centers of quasi-attractors and, simultaneously, the dynamics of the variation of the volumes of quasi-attractors Vg.
4. THE PROBLEM OF VOLUNTARY AND INVOLUNTARY TREMOR IS THE FIRST TYPICAL EXAMPLE OF TTS
TCS is closely related to chaos in biological systems, so the tremor is the basic process for TCS and medicine in general. If you carefully study the nature of involuntary movements of the hand of a human in normal or pathological in his attempts to keep limbs at a given point (postural tremor), it appears that, despite the large deviations of the limb from the set point, the motion is chaotic, the trajectories are not repeated, and it all happens within a certain volume of the phase space. This example, the organization of voluntary movement in effect (since the subject has to hold limb at a given point and the task is the sample is voluntary) shows the entire global challenge in the form of involuntary chaos TTS, i.e. voluntary task is realized by the body in the form of chaos TTS. In other words, the problem of voluntariness is implemented by the body in the form of chaotic (involuntary) implementation, and postural tremor is an example of involuntary mechanical act.
The chaotic nature of the movement of the state vector of the system may be observed in the phase plane and its parameters measured: the volume Vg of a quasi-attractor (volume of rectangle within which the state vector of the system travels, i.e., the coordinates x2 = V(t) and x1 = x(t) vary), the coordinates of the center of the quasi-attractor xc, and the matrix of interattractor distances (if there exist several states of the biological dynamic system and if Vg and xc are calculated for each state). Using these quantities, we may speak of the degree of chaoticity in the behavioral dynamics of complex biomedical systems.
Let us illustrate the method that has been developed for measurement of the parameters of microchaos in estimation of tremor. Something similar is observed for the other vectors that describe the human organism, which is demonstrated by the second example. This is a more general property of any state vector of the human organism that describes any biological dynamical system. In other words, tremor is a global property of biosystems, since in such a state any vector of a biological dynamical system that moves continuously in a phase space of states is constantly found in such a state.
A comparative analysis of the behavior of a dynamical motion control system in sighting and rest regimes was conducted in the phase plane by the method of multidimensional phase spaces [9], with the dimension of the phase space in the present case equal to 2. The phase portraits of the tremor, expressed in terms of the coordinates of the position of the finger and its speed of travel during and after sighting, are shown in Figures 1(a) and (b), where .
.
The values of the volumes of quasi-attractors (in the present example, this is the area of motion of the vector of the biomechanical system) of a given point were as follows: during sighting, ; following sighting,
; following sighting, 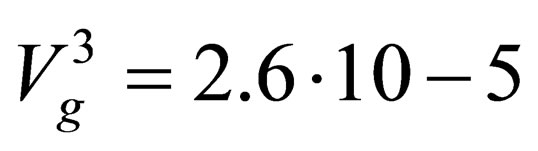 , i.e., Vg decreases 5.6-fold in the course of sighting, which characterizes the variation in the state of the system in the direction of a greater degree of chaoticity during the period of relaxation (following a decrease in drifts upon a command to hold). This in fact means that amplification of the degree of volition in the course of sighting reduces the microchaos parameters and characterizes quantitatively the degree of volition in tremor. The tremor parameters (as quasi-attractor) we use for identification of pathological state not only of neuropathological conditions but in case of different other types of diseases. The numerical examples of such application of QA we present in our previous articles [1,3,10].
, i.e., Vg decreases 5.6-fold in the course of sighting, which characterizes the variation in the state of the system in the direction of a greater degree of chaoticity during the period of relaxation (following a decrease in drifts upon a command to hold). This in fact means that amplification of the degree of volition in the course of sighting reduces the microchaos parameters and characterizes quantitatively the degree of volition in tremor. The tremor parameters (as quasi-attractor) we use for identification of pathological state not only of neuropathological conditions but in case of different other types of diseases. The numerical examples of such application of QA we present in our previous articles [1,3,10].
In this example with the tremor the problems of modern medicine, biology, psychology, philosophy, science and many other disciplines are formulated like in the crystal. This example reveals the essence and principles
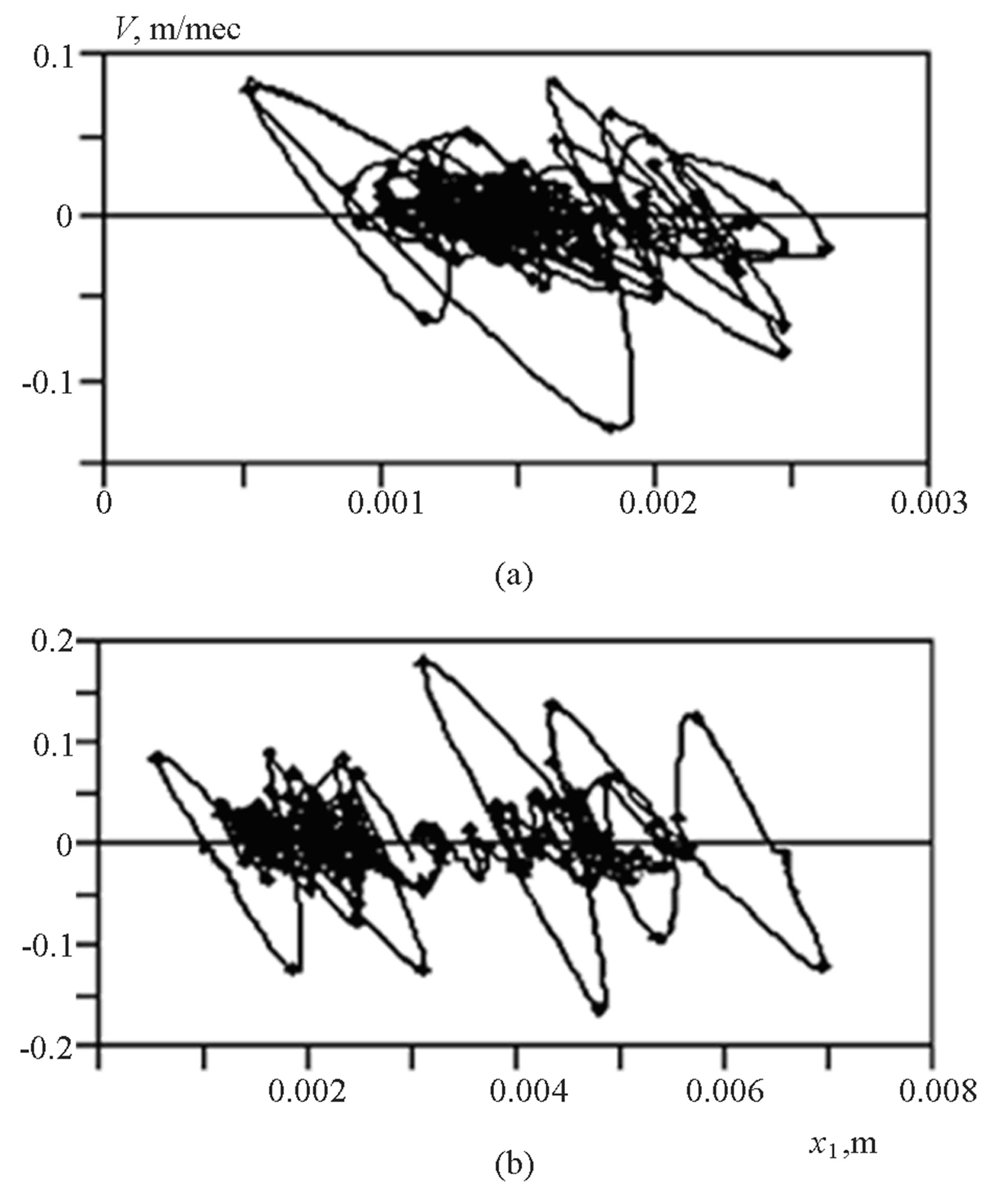
Figure 1. Phase portrait of tremor of extremity during (a) and after (b) sighting: x1—coordinates of position of finger, m; V— speed of movement, m/sec; x1 = x(t), x2 = V = —coordinates along the horizontal and vertical, respectively.
—coordinates along the horizontal and vertical, respectively.
of the PSS and brain work principles. This becomes very clear if we consider keeping the limb at point in space, as not DSP—stationary regime, when 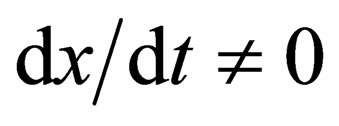 and
and 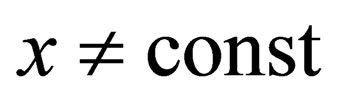 (i.e., “not the state of elasticity”), as well as a permanent adjustment to the position within the quasiattractor, i.e. as a continuous chaos when
(i.e., “not the state of elasticity”), as well as a permanent adjustment to the position within the quasiattractor, i.e. as a continuous chaos when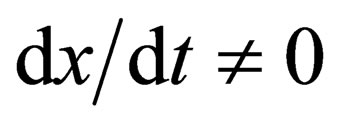 , actually! The parameters of such QA will be entirely dependent on the very posture and the condition of the entire body. Now we show that the parameters of the QA are markers of the internal brain state, PSS and the TCS tremor parameters can be diagnosed in the norm and the beginning of disease in the body. Chaos parameters in the form of quasi-attractors are informative chaos has information for physicians, biologists, and there is the main conclusion of the whole TCS. Uncertainty (chaos) creates certainty and predictability.
, actually! The parameters of such QA will be entirely dependent on the very posture and the condition of the entire body. Now we show that the parameters of the QA are markers of the internal brain state, PSS and the TCS tremor parameters can be diagnosed in the norm and the beginning of disease in the body. Chaos parameters in the form of quasi-attractors are informative chaos has information for physicians, biologists, and there is the main conclusion of the whole TCS. Uncertainty (chaos) creates certainty and predictability.
5. THE SECOND EXAMPLE OF CONSERVATIVE THERAPY ESTIMATION ACCORDING TO CHAOTIC DYNAMICS OF HEMOSTASIS PARAMETERS
We have performed a comparative analysis of the parameters of the quasi-attractors state vector in 7- and 6- dimensional PSS among patients with the lower extremities arteriosclerosis obliterans in the stage of critical ischemia treated with 4 different types of conservative therapy. The calculation of the parameters of quasi-attractors are made based on computer programs, registered in the Federal Agency for Intellectual Property, Patents and Trademarks (certificate number: 2006613212), Russia.
Were examined 186 patients aged 42 to 70 years, who came in 4 groups: group 1) patients receiving a standard, conventional medical therapy, group 2) patients received ozone therapy, in addition to standard therapy, group 3) patients treated with application payler-light in addition to the standard therapy, group 4) patients treated ozone therapy and applications payler-light in addition to standard therapy.
The study of D-dimers was carried out on the hemostatic system “CA-1500”, reagents “Siemens” were also used. Plasma was taken for research (tubes with sodium citrate). Additional tests: Soluble fibrin monomer complexes, XIIa-dependent fibrinolysis, Quick’s prothrombin index, homocysteine, partial intensified thromboplastin time, thrombin time, Antitrombin3, protein C and S, plasminogen performed using reagents domestic production “Technology standard” (Russia). Plasma was used (test tubes with sodium citrate). All these parameters have formed 13 components of human body state vector— HBSV in the PSS, which needed to calculate the quasiattractor.
Parameters for quasi-attractors HBSV comparison groups differ in terms of volume and the coordinates of their centers (stochastic and geometric) and a significant difference is detected when comparing plasma hemostasis in the third and fourth group. The most pronounced changes are observed in group 4. In group 1 and group 2 the effect of treatment is unstable, the changes are minor figures.
Thus, the HBSV characteristics depend on the type of therapy, it was found that different types of conservative therapy affect the different links of hemostasis. We found that ozone therapy greatly influences the fibrinolytic and platelet hemostasis, and treatment with the device bioptron more significantly affects the plasma hemostasis.
The use of different types of conservative therapy notes pronged effect on the hemostatic system with a pronounced effect of ozone therapy. It is obvious that only by applying complex conservative therapy we can achieve a stable therapeutic effect.
So all our investigations present the results: quasi-attractors parameter of the human organism state vector in the seven-dimensional phase space of states are more important changed than the results of statistical analysis of the primary data: fibrinolytic hemostasis initial volume Vx decreased by 4.5 times in the fourth group of the patients, in the second group—by 2.3 times. While in the 1st and 3rd groups the parameters are changed slightly. At study the parameters of the plasma hemostasis are significantly changed in the group 3 and group 4, where conservative therapy were combined with light-payler we see the increase of volume Vx in group 3 by 1.76 times, in the fourth one—by 2.73 times.
New methods of studying the state of the hemostasis mechanisms can be used to assess the adequacy and effectiveness of the therapy. This provides an approach to scientific prediction of hemostasis changes during conservative therapy with medicine and physiotherapy actions. It is extremely important to implement in clinical practice early recognition of the inadequacy of the organism’s reaction to treatment by calculating changes in the quasi-attractor parameters of HBSV.
6. THE THIRD EXAMPLE OF NEW DIAGNOSTIC METHODS FOR CALCULATION OF TYPE 2 DIABETES MELLITUS TREATMENT EFFECTIVENESS
One of the main problem of perspective non-control clinical research is connected with determination of integrative indicators of therapy quality of cardiovascular diabetic-autonomy neuropathy forms with α-lipoic (thioctic) acid. It is evident for us that our new method of quasi-attractor (QA) distances calculation according to the analyses of matrix with such quasi-attractor distances Zij (i and j—numbered QA) will be a good instrument for researching of dynamic system regulating human organism metabolic state.
So, 29 patients, aged 31 - 78, had been diagnosed with type 2 diabetes mellitus (DM) is the object if our research. The middle disease period is equal to 8.96 ± 4.56 years, average glucose level is equal to 5.73 ± 0.52 millimole per liter. For all patients we provide special therapy with a-lipoic (thioctic) acids 600 mg a day during two weeks (intravenously). We exclude patients with neuropathy (type III), with compromised liver function, with chronic disease of respiratory organs, with heart valvate pathology, with III and IV functional class of chronically cardiovascular collapse, with instable angina pectoris, with heart-operated (last 6 month), other hard diseases in an acute condition. The study was approved by the local research ethics committee.
Diagnostics of neurovegetative maintenance of a patient organism with type 2 DM is based on research of heart rhythm variability (HRV) with definition of time and its frequency characteristics. The condition of cardiorespiratory system of patients with DM 2 was estimated on original cardiorespiratory system’s index with usage of pulseoxymeter “Eloks-01C2” (“New Devices”, Samara) within the limits of the author’s developed techniques of Samara and Surgut schools of medical cybernetics (Prof. L. I. Kalakutsky, Prof. V. M. Eskov). The spectral analysis of vibrational VRS structure was made by means of photooptical sensor and the specialized program bundled software on the basis of the computer.
Arraying of inter-attractors’ distances of state vector movement of patients with DM 2 was made on the basis of paired comparison of distances between all pairs quasiattractors centers movements of HRV before and after parenteral α-lipoic acid introduction in following control points of observation: I—the beginning of therapy (initially); II—on completion of control observation by α- lipoic acid therapy (for 14 day), and II/I—in a control point “on completion of control observation by α-lipoic acid therapy” in relation to a control point before the beginning of therapy (initially) (Table 1).
At calculation of distances Zkf between HRV quasiattractor centers of patients with DM 2 receiving α-lipoic acid therapy the data of 5 quasiattractors HRV patients with DM 2 in 3 points of control observation is used. As the quality indicator of parenteral α-lipoic acid introduction influence on the functional systems regulating HRV, indicator Zij of a distance matrix is presented.
Coordinates of general 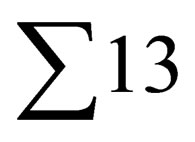 -m-phase space of conditions are all analyzed diagnostic HRV signs. In general quasiattractor subpopulations of the most homogeneous signs—“clusters” have been allocated: 5-m PhSS “spectral characteristics HRV” (x0—VLF (ms2); x1—LF (ms2); x2—HF (ms2); x3—LF/HF; x4—Total P (ms2)), 3- m PhSS “Structure spectral characteristics HRV” (x0—
-m-phase space of conditions are all analyzed diagnostic HRV signs. In general quasiattractor subpopulations of the most homogeneous signs—“clusters” have been allocated: 5-m PhSS “spectral characteristics HRV” (x0—VLF (ms2); x1—LF (ms2); x2—HF (ms2); x3—LF/HF; x4—Total P (ms2)), 3- m PhSS “Structure spectral characteristics HRV” (x0—
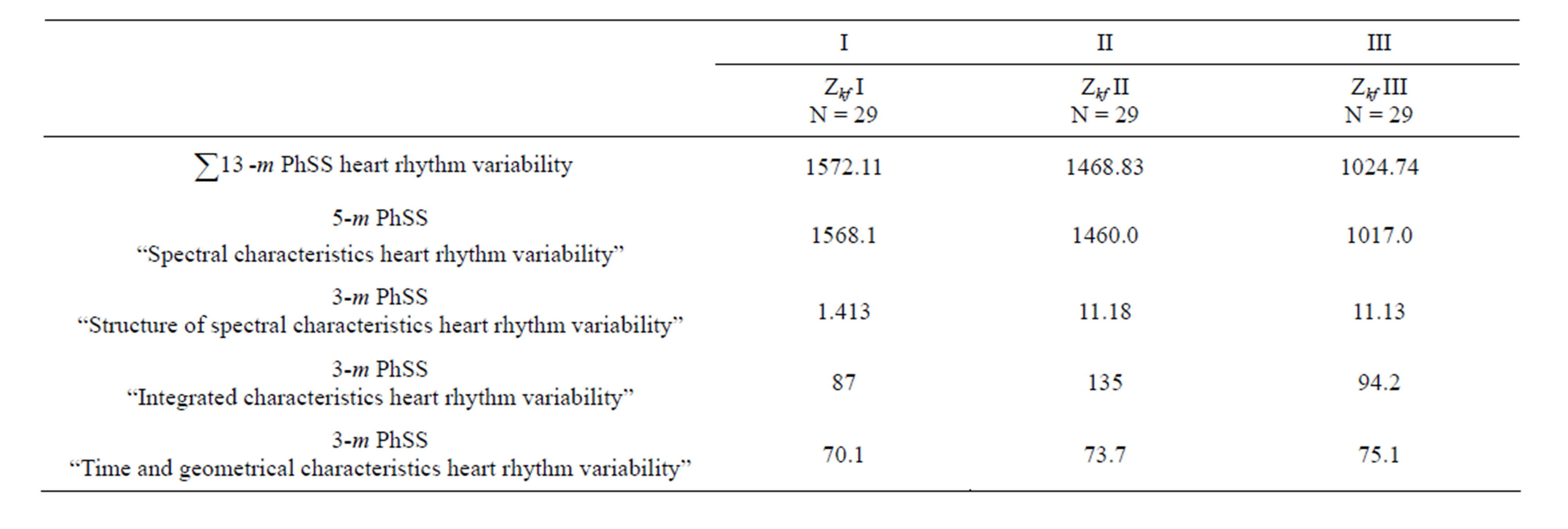
Table 1. Results of distance calculation (Zkf) between quasiattractor heart rhythm variability centers of patients with type 2 diabetes mellitus receiving α-lipoic acid therapy on 3rd intervals of control observation.
LF%; x1—HF%; x2—LF/HF), 3-m PhSS “Integrated characteristics HRV”, 3-m PhSS “Time and geometrical characteristics HRV” (x0—SDNN (ms); x1—HRV; x2— R-R (ms)).
From given facts (table) the expressed positive influence of parenteral α-lipoic acid introduction on HRV regulation is revealed in the first days (Zkf I 1572.11), further efficiency tends to decrease by 14 day though remains enough high (Zkf II 1468.83). Value Zkf in III point of control observation corresponds to criterion integrative qualities ECA for all period of observation (Zkf III 1024.74).
At subcluster analysis of clinical efficiency of α-lipoic acid in each subpopulation of the most homogeneous HRV signs, following tendencies have been revealed. Dynamics of spectral HRV characteristics in 5-m PhSS, analyzed on the quality indicator—Zkf, reflects the expressed metabolic effects of α-lipoic acid on 600 mg/ days at the first parenteral introduction (Zkf I 1568.1) which tend to decrease on termination of control supervision (Zkf II 1460), and, as a whole, correspond to high enough values (Zkf III 1017) for all period of observation.
So, the indicator of quantity Zkf is a quantitative measure of effectiveness of our medical influence on patient’s organism. Such effectiveness was based on distance measurement between the statistical quasi-attractor centers (chaotic approach) in multidimensional phase spaces. It is established that parenteral α-lipoic acid introduction of 600 mg/day leads to expressed heart rhythm variability modulation at the first introduction of a preparation, further effectiveness remains during all period of observation and corresponds to high values for all period of observation as a whole.
Integrative indicators of our therapies quality (calculated with the help of inter-attractors’ distance matrixes of heart rhythm variability of phase space of state) prove the expressed metabolic effects of parenteral α-lipoic acid introduction in complex therapy cardiovascular forms of diabetic autonomic neuropathy of our patients with type 2 diabetes mellitus.
7. THE BASIC AND GLOBAL PRINCIPLES OF IM AND THE NECESSITY OF THEIR IMPLEMENTATION
1) Any parameters of the human body state vector— HBSV (postural tremor, heart rate, EEG, biochemical parameters of blood, tissues in health and disease) perform random motions within certain regions of phase space, which we designate as the quasi-attractor (QA). Parameters of QA—a chaotic parameters HBSV and though chaos is the minimum uncertainty, but it gives rise to certain parameters and serve as diagnostic signs in medicine and biology. Uncertainty creates certainty in the form of QA volumes and distance matrices between quasi-attractors centers.
2) Any chaotic dynamics TTS is estimated by QA parameters and it is an important characteristic of the biological (medical) of the object, its evolution and prediction of the final state. By measuring the QA, we can judge the voluntariness and involuntariness in the organization of movements, and thus show the unity of voluntariness and involuntariness, the unity of chaos and order, certainty and uncertainty. This also applies to any other parameters of homeostasis.
3) Parameters of the QA represent the individual properties of the body integrative and quantitatively, can be a measure of the state of homeostasis (whether the body is able to normogenesis or pathogenesis) and, most importantly, they are the individual integrative parameters of a certain human (animal). The last opens new perspectives for the development of personelized medicine. Each person can have his own phase portrait (own personal spacecraft) to different clusters of measurements (biomechanics, biochemistry, heart work, psyche, etc.). We could dream of it in the time of I. P. Pavlov and P. K. Anokhin and now these dreams are realized in practice by TCS, specific methods and approaches.
4) New perspectives in the field of medicine and the whole individual, particularly, are appearing, since integrative indicators not only for certain types of diseases are appearing too, besides for everyone (individual QA) under the various types of pathology. We obtained samples: what one person is the norm for the other may be an area already PSS corresponding pathology and vice versa. There are new prospects for practical medicine, experimental biology, ecology and other natural sciences. Moreover, the example of the tremor now shows complete inversion of concepts: chaos in the dynamics of tremor is the norm for the body, it is a stationary regime, on the contrary, the appearance of the frequency and the more stationary states ( ) are abnormal, and in final form—the death of the body. Our great predecessors (I. P. Pavlov and P. K. Anokhin, W. Weaver, I. R. Prigogine) felt it, but they were not able to quantify this measure. Nowadays TCS gives such an opportunity [11].
) are abnormal, and in final form—the death of the body. Our great predecessors (I. P. Pavlov and P. K. Anokhin, W. Weaver, I. R. Prigogine) felt it, but they were not able to quantify this measure. Nowadays TCS gives such an opportunity [11].
5) The main task of IM is defining the order parameters—OP, most importantly, the main diagnostic features. There OPs can be individual for each human (after all, every one of us dies for special reasons, individually). Now TCS has developed three approaches to minimize the phase space and find the order parameters. We have proved that one (or more) iterations while using neurocomputer does not allow to set the OP. We have developed another procedure, including TCS for using IM.
6) In general, the entire IM should be based on fundamental principles of TCS, which covers the entire biomedical sciences:
a) Any SSV has chaotic dynamics within the QA, QA parameters are informative for IM. It is a microhaos of SSV.
b) The evolution and teleological movement of SSV in the PSS has macrochaotic basis and for coping with this chaos, we need necessary ECAs (defined within IM).
c) IM needs a continuous, long-term monitoring of SSV in the PSS, otherwise we may miss “tongues” of mortal QA (hitting SSV in MA). Such “tongues” are harbingers of future changes (they increase the VG for QA) and they need to be monitored and prevented with the help of ECAs. Any variation of SSV in the PSS are informative!
d) IM demands the identification methods of OP for a single patient, as we are now trying to do in the case of the endemic features of the SSV. It is necessary to do endemic for everyone (7000,000,000 QAs and their properties!). The fact that we like each other is the result of similar mechanisms of self-organization within our bodies, but their implementation is always chaotic and individual. Chaos is not defined, but it is unique at the same time [1,7,9,11].
e) Setting the necessary ECAs should be based on individual OP, his QA, abnormalities, monitoring the QA evolution in the PSS. We need new cybernetic methods of continuous monitoring and instant decision-making according to ECAs. It’s like a labor: no one knows the hour and minute of birth, but they are possible to be predicted, to cause artificially at the right time (and not in the cart, train or plane voluntary). There is no need to bring the body to the irreversible crisis hit in MA. Much of what we have already done is (but in a primitive way, without TCS) in traditional oriental medicine.
REFERENCES
- Eskov, V.M., Eskov, V.V. and Filatova, O.E. (2011) Characteristic features of measurements and modeling for biosystems in phase spaces of states. Measurement Techniques (Medical and Biological Measurements), 53, 1404- 1410.
- Eskov, V.M. (2011) Third paradigm. Samara, Ofort.
- Gavrilenko, T.V., Baltikova, A.A., Degtyarev, D.A. and Pashnin, A.S. (2012) The comparison of the efficiency of classic stochastic theory and theory of chaos-self organization (TCS). Complexity Mind Postnonclassic, 1, 81-91.
- Eskov, V.M. (1996) Models of hierarchical respiratory neuron networks. Neurocomputing, 11, 203-226. doi:10.1016/0925-2312(95)00048-8
- Eskov, V.M. (1994) Direct control by dissipation factor in respiratory neuron networks. Neural Network World, 6, 663-670.
- Eskov, V.M. (1995) Hierarchical respiratory neuron networks. Modelling, Measurement & Control, 48, 47-63.
- Eskov, V.M., Eskov, V.V., Filatova, O.E. and Filatov, M.A. (2012) Two types of systems and three types of paradigms in systems philosophy and system science. Journal of Biomedical Science and Engineering, 5, 602- 607. doi:10.4236/jbise.2012.510075
- Weaver, W. (1948) Science and complexity. Rockefeller Foundation, New York.
- Eskov, V.M., Eskov, V.V. and Filatova, O.E. (2010) Characteristic features of measurements and modeling for biosystems in phase spaces of states. Measurement Techniques, 53, 1404-1410. doi:10.1007/s11018-011-9673-4
- Filatov, M.A., Filatova, D.Y., Himikovam, O.I. and Romanova, J.V. (2012) Matrixes of quasiattractor distances at identification of human psychophysiology function. Complexity Mind Postnonclassic, 1, 19-24.
- Third Global Paradigm. http://www.thirdglobalparadigm.com/home/manifesto
NOTES
*The authors report no conflicts of interest in this work.

