Journal of Geographic Information System
Vol.07 No.04(2015), Article ID:58934,7 pages
10.4236/jgis.2015.74034
The Combination Operator of Information Sources by a New Expressive Matrix
A. Boualem1, Y. Dahmani2, A. Maatoug2
1High National School of Computer Science, ESI, Algiers, Algeria
2The EECE Lab, Ibn Khaldoun University, Tiaret, Algeria
Email: ab_boualem@esi.dz, dahmani_y@yahoo.fr, maatoug_aek@yahoo.fr
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 24 June 2015; accepted 16 August 2015; published 20 August 2015
ABSTRACT
The multi-sensors fusion refers to the synergistic combination of sensory data from multiple sensors to provide more accurate and reliable information. The potential benefits of the Fusion are multi-sensors’ redundancy and extra information acquired. The fusion of redundant information can reduce the overall uncertainty and thus helps to provide information specified more precisely. Several sensors providing redundant information can also be used to increase reliability in the case of error, omission or failure of sensors. The combination operators are exponential and are more complex in terms of calculation; the Dempster-Shafer operator is exponential for more than three (3) information sources [1] [2] . Our work focuses on the definition of another formulation of this operation, and puts it in a matrix form to illuminate the computational complexity, more precision guaranty and a minimal execution time. We propose to use each information source in a form of a matrix, which contains 0 value in lines that do not contain the masses (m(Ai) = 0) or once m(Ai) is not null (m(Ai) ≠ 0). The use of this expressed matrix attempts to ameliorate Dempster-Shafer operator via initialing either a criterion or criteria sources’ solution, increasing the efficiency of the Dempster-Shafer operator and facilitates the combination among the sources. We evaluate our approach by conducting a case study for showing the effectiveness of this matrix.
Keywords:
Dempster-Shafer Operator, Fusion Process, Criterion Information Sources, Criteria Information Sources, Conflict Managing, Reliability Factors, Decision

1. Introduction
The technological evolution of MEMS (Micro-Electro-Mechanical System) and Wireless Communication Tech- nology in recent years has taken an upward path for the accuracy of the precision decision, calculation, monitoring and environmental sensation, minimizing energy consumption, cost, shape, etc.
Modern technology shows that it is possible that an information source can give more additional information on several criteria; it is easy to find a source informational criterion which gives information about the geometric criteria (Euclidean distance, the shape, and the area at a time), and another source informational criterion provides information on two or more criteria at once (both of geometric and topographical criteria), that is to say, it can capture multiple heterogeneous information such as the example of a source can capture the Euclidean distance and semantic distance. This paper shows the intended use of these types of sources which enrich the information in terms of:
Obtaining and providing a validation of information provided by different criteria sources;
Remedying the deficiency of geographic data based on the matching operation;
Validating the operator Dempster-Shafer for a broad and extensive use.
Information fusion has evolved significantly in recent years in various fields, especially in Information Systems, Vision, Robotics and Wireless Sensor Networks (WSNs), the information sources have increased in the sense that its sensors nodes had been a priori and generic knowledge information. Each information source is generally imperfect; it is important to combine more information to have a better understanding of the real world. Information fusion can then be defined as (often imperfect and heterogeneous) combinations of information to obtain more complete information and better quality, and improved to decide and act. Because the methods for modeling information knowledge were Imperfect, their combinations know major theoretical developments and many experiments have been expanded towards their application areas. These methods, often from theories of decision making, uncertainty and artificial intelligence, can be numeric or symbolic. In general, the alarming increases the Fusion of information that takes the technology and information processing.
The information handled in a combination process is firstly the information to be fused, and secondly additional information used to guide or support the combination operation. It may be information on combining information such as information on sources, on their dependence and on their reliability, preferences on information combining, etc. They may be also of contextual information on the field.
In general, the fusion is not a simple task. It can be broken down into several tasks schematically. The main steps to resolve for build the fusion process are:
Modeling: This step involves choosing the formalism, and the expressions of the information to be fused into this formalism;
Estimation: Most models require estimation phase (i.e. all methods using distributions);
Combination: This step is the selection of an operator compatible with the chosen modeling formalism and it is guided by additional information;
Decision: This is the final step of the fusion process, which can go through information provided by the sources towards the selection of a final and best decision.
There is enormous literature on the critique of combination operators and on the new combination operators. The first operator was known as Dempster-Shafer [3] , which was strongly criticized by several definitions of other operators such as Smets [4] , Yager [5] and Dubois and Prade [6] , but the Dempster operator was the only operator that showed its effectiveness until today to combine uncertain information from different sources. In this article we try to refine the combination operation in expressive matrix; so, both source informational criterion sources and criteria aim to minimize the computational complexity, and improve the reliability and accuracy of decisions. The rest of this article is organized as follows: Section 2 cites various related works on different combination operators; Section 3 shows the combination formalism of criterion information sources; Section 4 presents the formalism of the combination of sources informational criteria; Section 5 presents our contribution to expressing the combination operators in matrix formula; Section 6 shows the evaluation of this technique by study case that makes a comparison among the classical formalism, criterion and criteria information sources participating in the combining step process; Section 7 ends this paper with a general conclusion.
2. Related Work
In the literature, there are two types of combinations; the first type is the combination of reliable sources, the second is the combination of unreliable sources; the first is the same idea as the operator of Dempster-Shafer [3] [7] and Smets [4] , they consider that the sources are reliable and combine the evidence for this conflict is a problem comes from not taking into account one or more assumptions in the frame of discernment. So it affects the conflicting mass (K) to the empty set . This combination is then defined by the following formula:
. This combination is then defined by the following formula:
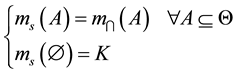 (1)
(1)
Yager offers a similar approach in [5] based on the introduction of a new hypothesis in the frame of discernment. This hypothesis will accept any conflicting mass. Moreover, one can notice that operators assuming that the sources are reliable mainly based on a conjunctive combination.
The second type (combination of unreliable sources) considers that the conflict can be generated by a defect reliability of some of the information sources. This argument was taken up in the context of operators introduced by Yager [5] and Dubois and Prade [8] . In the case of the operator Yager [5] , it is assumed that one of the sources involved in the combination is reliable. Thus, the solution is necessarily within discernment. But not knowing which source gives the true solution, Yager proposes to assign the conflicting mass (K) to all Θ. The resulting mass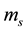 , of this combination for two sources information {S1, S2}, is obtained as follows:
, of this combination for two sources information {S1, S2}, is obtained as follows:
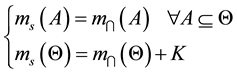 (2)
(2)
The combination formula Proposed by Dubois and Prade in [8] , as part of the fusion of two sources of information combination {S1, S2}, can be explained as follows. S1 is a source supporting the proposal B with belief mass 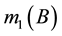 and S2 is a source supporting the proposal C with a belief mass
and S2 is a source supporting the proposal C with a belief mass 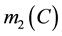 . When the proposals supported by both sources are contradictory and not knowing which source is reliable, the principle of minimum specificity required to redistribute the mass associated with this contradiction, either
. When the proposals supported by both sources are contradictory and not knowing which source is reliable, the principle of minimum specificity required to redistribute the mass associated with this contradiction, either 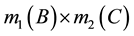 is the union of the proposals, is to say
is the union of the proposals, is to say 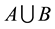 .
.
The operator of Dubois and Prade is then defined as follows for two sources of information:
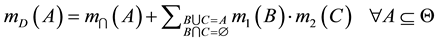 (3)
(3)
This work based on a complex linear combination in terms of computation especially if using more than tow (2) sources, more such combinations are not applicable if using new technologies which consists of Criteria Sources such as Sensors, Radar. This work consists of the combination operators include traditional information sources and new operators.
3. Criterion Sources
In his work, Shafer [9] proposed the combination rule of Dempster, symbolized by ? to combine or to Fusion two distinct information sources named: Combination Dempster-Shafer operator.
Let  and
and 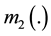 Two sets of masses associated respectively with belief functions
Two sets of masses associated respectively with belief functions 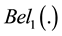 and
and 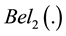
on the same frame of discernment Θ. The overall function of belief is obtained, under the Dempster-Shafer Theory (DST) from the combination sets of mass 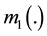 and
and  . Let
. Let 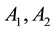 are respectively two (2) portions of Θ supported by the sources
are respectively two (2) portions of Θ supported by the sources


which 
4. Criteria Sources
Define abbreviations and acronyms the first time they are used in the text, even after they have been defined in the abstract. Abbreviations such as IEEE, SI, MKS, CGS, sc, dc, and rms do not have to be defined. Do not use abbreviations in the title or heads unless they are unavoidable.
A Criteria or Multi-Informational source is a source that can provide more information at once for a given object. Let 

which 
5. The Contribution
5.1. Units Expression of Matrix Operator Combination
Either 


Either 



Let the sets of masses:

5.2. Expression of Criterion Combination Matrix
Let


The combination of these two sources under the new Mono-Criteria Dempster-Shafer theory is as follows:

Our contribution is to redefine this Criterion operation by a matrix equation:

That is to say we can express


5.3. Expression of Criteria Matrix combination
Let


The combination of these two sources as the new Advanced Dempster-Shafer operator is as follows:

6. Case Study
We try in this case study to provide examples that demonstrate the usefulness of each type of operator (either with a Criteria, Criterion with or without reliability coefficients), especially the reduction of the computational complexity if there were more sources information to combine.
6.1. Expression of Criteria Matrix Combination
Let 


The matrix representation of these sources is as follows:
Each information Source



The combination is defined by the following matrix:

That is to say:

The algorithm complexity is 

6.2. Example 2: Criteria Sources
Let



The matrix representation of these information sources is as follows:
Explode each source





Combination is defined by the following matrix:


so

so
So:

7. Conclusion
In this article we expressed the operator of combining informational sources in expressive matrix, at the expanse of Dempster-Shafer operator, the Smets operator, the Yager operator, Hedging Technique, and Dubois and Prade operator. This expressive matrix is very effective in simplifying the complexity of the calculation (algorithm complexity) and is managing the conflict among informational sources in their origin. Indeed, this expressive matrix participates in simplifying the combination of two or more sources in a simple way, generalizes the operation of combination among informational sources in criterion and criteria information sources, and overcomes problems encountered in combination phase. In addition, we have shown its effectiveness in a case study of compared with the traditional expression.
Cite this paper
A.Boualem,Y.Dahmani,A.Maatoug, (2015) The Combination Operator of Information Sources by a New Expressive Matrix. Journal of Geographic Information System,07,430-437. doi: 10.4236/jgis.2015.74034
References
- 1. Martin, A. (2005) La fusion d’informations. Polycopié de cours ENSIETA, 1484.
- 2. Martin, A., Sévellec, G. and Leblond, I. (2004) Characteristics vs. Decision Fusion for Sea-Bottom Characterization. Journées d’Acoustique Sous-Marine, Brest, 19-20 October 2004.
- 3. Dempster, A.P. (1967) Upper and Lower Probabilities Induced by a Multi-Valued Mapping. Annals of Mathematical Statistics, 38, 325-339. http://dx.doi.org/10.1214/aoms/1177698950
- 4. Smets, P. (1990) The Combination of Evidence in the Transferable Belief Model. IEEE Transactions on Pattern Analysis and Machine Intelligence, 12, 447-458. http://dx.doi.org/10.1109/34.55104
- 5. Yager, R. (1987) On the Dempster-Shafer Framework and New Combination Rules. Information Sciences, 41, 93-138. http://dx.doi.org/10.1016/0020-0255(87)90007-7
- 6. Dubois, D. and Prade, H. (1986) On the Unicity of Dempster Rule of Combination. International Journal of Intelligent System, 1, 133-142. http://dx.doi.org/10.1002/int.4550010204
- 7. Dempster, A.P. (2008) The Dempster Shafer Calculus for Statisticians. International Journal of Approximate Reasoning, 48, 365-377. http://dx.doi.org/10.1016/j.ijar.2007.03.004
- 8. Dubois, D. and Prade, H. (1988) Representation and Combination of Uncertainty with Belief Functions and Possibility Measures. Computational Intelligence, 4, 244-264.
http://dx.doi.org/10.1111/j.1467-8640.1988.tb00279.x - 9. Shafer, G. (1976) A Mathematical Theory of Evidence. Princeton University Press, Princeton.

















