Natural Science
Vol.4 No.11(2012), Article ID:24863,13 pages DOI:10.4236/ns.2012.411116
A potential energy profile of the catalytic cycle of pyruvate decarboxylase
![]()
Dipartimento di Chimica, Università di Torino, Torino, Italy; *Corresponding Author: carlo.canepa@unito.it
Received 27 August 2012; revised 30 September 2012; accepted 11 October 2012
Keywords: Pyruvate Decarboxylase; Mechanism
ABSTRACT
A computational study on the mechanism for the decarboxylation of pyruvic acid to acetaldehyde catalyzed by pyruvate decarboxylase at the B3LYP/6-31G (d, p) level of theory is presented. The model employed is self-contained and it does not resort to external groups to provide protons to the various structures in the mechanism. The potential energy surface points at the intramolecular proton transfer from the amino group of the pyrimidine ring in the enamine intermediate to the enol exocyclic carbon as the rate-determining step (with a barrier of 20.55 kcal·mol–1). This value is in reasonable agreement with an estimated barrier of 24.76 kcal·mol–1, derived from the experimental rate constant (4.0 × 10–5 s–1) for the decarboxylation of α-lactylthiamin.
1. INTRODUCTION
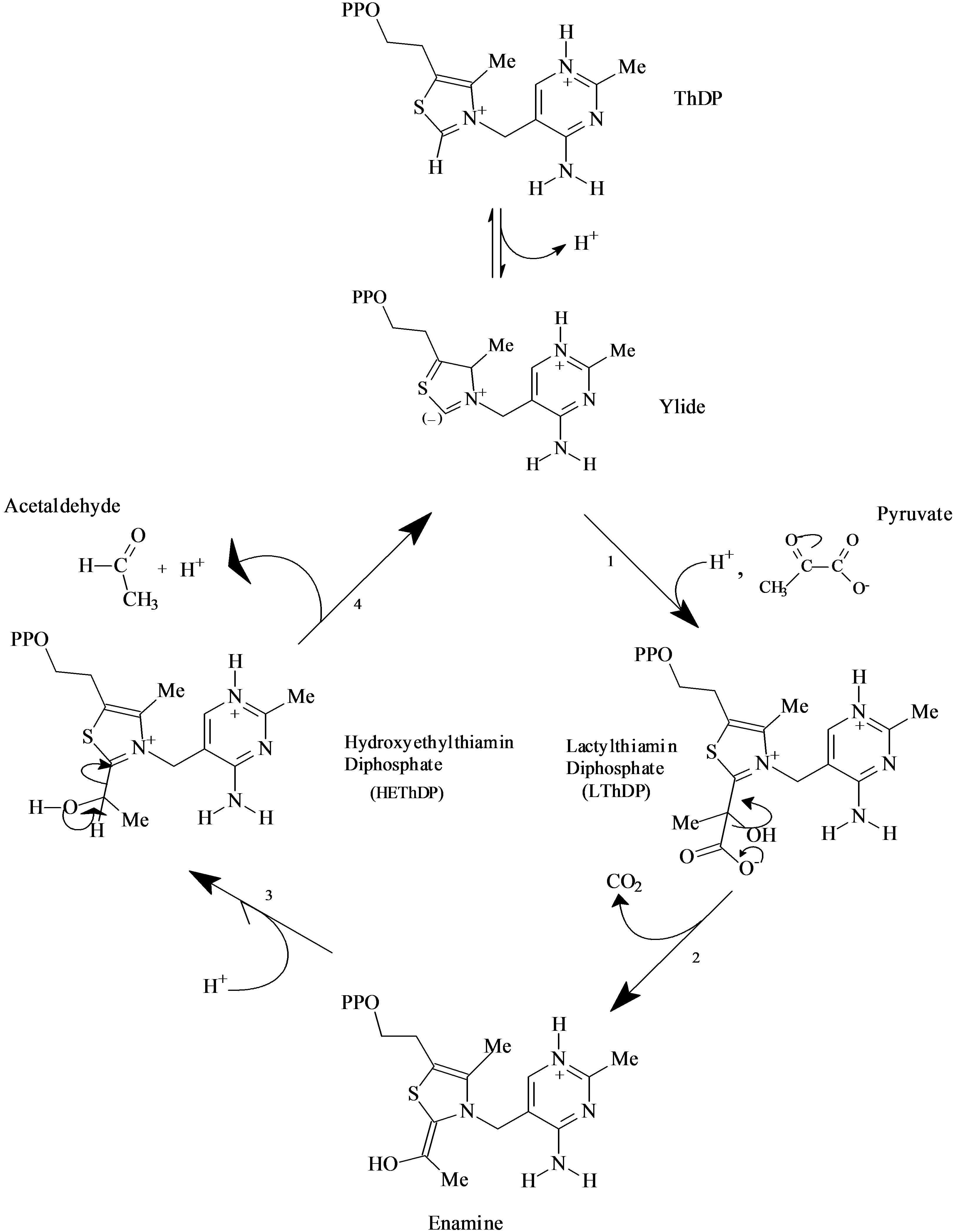
Pyruvate decarboxylase (PDC, EC 4.1.1.1) is a 240 kDa protein [1] that belongs to the lyase carbon-carbon class of enzymes. Its catalytic activity is essential for several metabolic pathways in both prokaryotes and eukaryotes. Typical reactions catalyzed by PDC are the decarboxylation of α-ketoacids in alcoholic fermentation, and the transfer of keto groups among carbohydrates in gluconeogenesis. The most studied PDCs occur in yeasts and bacteria as Saccharomyces cerevisiae (ScPDC) and Zymomonas mobilis (ZmPDC). The structures of ZmPDC and ScPDC were determined by X-ray diffraction at 2.3 Å resolution [2]. In particular, ScPDC crystallizes in an asymmetric unit made of two subunits, but in physiological conditions it assumes homotetrameric form. The individual subunits, formed by a single polypeptide chain, include two topological forms (named α and β), divided in turn into three structural domains. The subunits have a catalytic site with one molecule of the coenzyme thiamin diphosphate (ThDP, see the APPENDIX section for a list of the abbreviations), and one magnesium cation bonding to six molecules of water.
The role of thiamin diphosphate in catalysis has been extensively reviewed by Kluger and Tittmann [3]. While both thiamin diphosphate and Mg2+ are essential for the catalytic activity of PDC, only ThDP directly participates with its two rings in the mechanism [4,5] (Scheme 1).
The estimated rate enhancement attained by PDC with respect to the uncatalyzed reaction is 1012 [6]. For comparison, the rate of the ThDP-catalyzed reaction is 106 times slower with respect to the process catalyzed by the full enzyme [2]. The difference in activation free energies between the reaction catalyzed by ThDP only and the corresponding enzymatic process was estimated to be 5 - 6 kcal·mol–1, based on square-wave voltammetry measurements [7]. In ThDP a thiazolium ring and a pyrimidine ring are connected by a methylene bridge (Scheme 2), and interactions with the amino acids at the active site determine its “V” conformation [8], with the two heterocycles eclipsed [9]. The hydrogen bonds responsible for both the stabilization of the “V” conformation and the close proximity of the pyrimidine N4’ and the thiazolium C2 are Glu50-N1’, Gly413-N4’, and Ile415-N3’.
Scheme 1 reports the classical mechanism of catalysis of ScPDC, summarized in five steps: 1) Deprotonation of ThDP with formation of the ylide/carbene; 2) Nucleophilic addition of the ylide/carbene to pyruvate with formation of the intermediate LThDP; 3) Decarboxylation of LThDP and formation of the enamine intermediate; 4) Proton addition to hydroxyethyl-ThDP with formation of HEThDP; 5) Acetaldehyde release and regeneration of the ylide/carbene.
The proton loss from C2 of the N-alkyl thiazolium salt gives the ylide/carbene species stabilized by the adjacent nitrogen and sulfur atoms, which determine the nucleophylicity of ThDP in the first catalytic step. It has been established that the H/D exchange at C2 is impaired when the glutamate interacting with N1’ is substituted in mutant yeast PDC [10], and the pKa of the C2-H is 109 times larger in the enzyme than in water solution [1]. This difference in the pKa values corresponds to a stabilization of the zwitterionic enamine intermediate by PDC of at least 13 kcal·mol–1. The generation of the ylide/carbene at the
Scheme 1. The five steps of the classical catalytic cycle of PDC.
active site is assisted by highly conserved amino acid residues in the various forms of PDCs.
Both the nitrogen atoms at the 4’ and 1’ positions are required for activity [11], but Jordan argues that the exocyclic nitrogen in the 4’-aminopyrimidine ring is not suitable for acid-base catalysis [12]. The glutamate residue at a short distance from the N1’ atom is thought to promote the amino-imino tautomerization (Scheme 2). Mutagenesis studies showed that there is no substitution of acid or base group at the active site that fully abolishes the activity, supporting the participation of the coenzyme in all proton transfers along the pathway.
The cofactor ThDP can exist in two tautomeric forms, i.e. the 4’-aminopyrimidine with an -NH2 group bound to the C4 of the aromatic pyrimidine, and the 1’,4’-iminopyrimidine, with the =NH moiety bound to the C4 of the quinoid pyrimidine. Based on circular dichroism (CD) signals on ThDP-dependent enzymes, Nemeria [13] concluded that the 1’-4’-imino form is the favored tautomer in all tetrahedral ThDOP adducts on all pathways. The

Scheme 2. Interconversion between the tautomeric forms of ThDP.
molecular dynamic simulation (MDS) of Schiøtt [8] on the catalytic active site of the PDC of Zymomonas mobilis individuated Glu50 and Glu473 as the most important amino acid residues for establishing the tautomeric equilibrium between 4’-aminopyrimidine and 1’,4’-iminopyrimidine. The proton relay interconverting the two tautomeric forms is not reported to be direct, but mediated by two water molecules.
Direct detection of the steady-state concentrations of the reaction path intermediates by 1H NMR spectroscopy allowed Tittmann to obtain the rate constants of the elementary steps of the catalytic cycle [14]. The rate constant for H/D exchange in the enzyme is five orders of magnitude greater compared to the corresponding rate for free ThDP ((1.1 ± 0.2) × 102 s−1 and (9.5 ± 0.4) × 10−4·s−1 for the enzyme-bound ThDP and free ThDP [10], respectively). The decarboxylation and acetaldehyde release steps in ZmPDC resulted to be rate-limiting with the respective rate constants of 397 ± 20 s–1 and 265 ± 13 s–1. The important interactions between the amino acid residues at the active site and the various intermediates in decarboxylation reactions catalyzed by ScPDC and ZmPDC are also pointed out in the study by Tittmann, as is the role of the exocyclic 4’-amino group. On the contrary, the carbon kinetic isotope effect study by Huskey [15] on wild type PDC is consistent with the rate-limiting step to be the addition of C2 to the carbonyl of pyruvate. On the other hand, in indolepyruvate decarboxylase [16] the rate-limiting steps in the catalytic cycles are the nucleophilic attack to the carbonyl (1.25 and 18.45 s–1 for pyruvate and benzoylformate as substrates, respectively) and the product release (3.46 and 37.10 s–1 for pyruvate and benzoylformate, respectively). The release of product involves the hydrogen bond between Glu50 and N1’ of the pyrimidine ring, while the His113 and Asp27 residues are important in the carbon protonation of the enamine.
A few computational studies on various aspects of the PDC catalytic cycle are available in the literature. The investigation by Li [17] estimated the decarboxylation barrier in the protein environment to be 16.0 kcal·mol–1, but the relevant transition structure could not be located. The transition structure for proton transfer from His115/ Asp27 to the aldehyde carbon atom lies 39.58 kcal·mol–1 above the enamine. Since it is argued that the release of acetaldehyde has a barrier of 7.91 kcal·mol–1 with respect to HEThDP, the rate-limiting steps are decarboxylation and carbon protonation. The rotational barriers of the 4’-amino group for thiamin, N1’-protonated thiamin, and N1’-methyl-thiamin were also computed by Friedemann [18].
The recent computational study by Schiøtt [19] supports the direct proton abstraction from the C2 by the imino N4’ to afford the ylide/carbene with a barrier of 7 - 9 kcal·mol–1. The corresponding process mediated by water as a model of the amino acid residues at the active site exhibits the higher barrier of 13.5 kcal·mol–1.
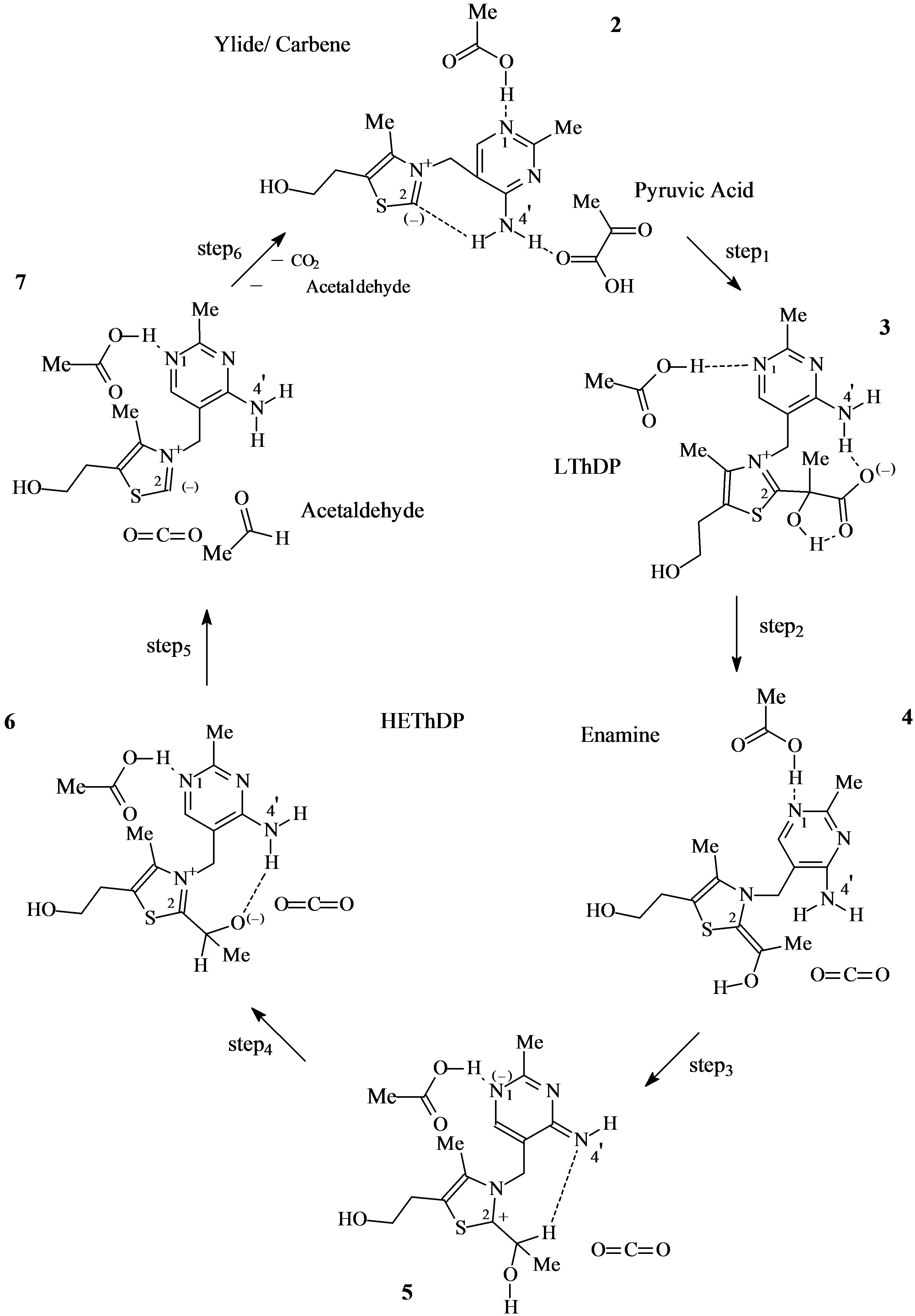
In this study we aimed at a complete potential energy profile relative to all the steps in the catalytic cycle which could only be obtained with a constant mass model. In the proposed mechanism we conserved the number of atoms in all the elementary steps, and included a sufficiently large system to exhibit an overall zero charge (see Scheme 3 in the Discussion). We could thus provide all the critical points relevant to the catalytic cycle, and were able to avoid the introduction of species external to the mechanism. Doing this, we give the full potential energy profile with the same energy reference.
Scheme 3. The mass-conserving catalytic cycle of PDC.
2. METHODS OF CALCULATION
Quantum chemistry calculations were carried out using the Gaussian 03 suite of programs [20], utilizing redundant internal coordinate geometry optimization [21]. All structures were fully optimized at the B3LYP [22,23] level of theory with the 6-31G (d, p) basis set. Since it has been observed that geometries and energies are not affected by low polarity solvents, solvation calculations were omitted on the basis of the low dielectric constant of the protein environment (2 - 4) [19]. Vibrational frequency calculations were used to characterize all stationary points as either minima or first-order saddle points at the level indicated. The partition functions were evaluated at 298 K and 1 bar. The partition functions were calculated within the rigid-rotor harmonic-oscillator approximation [24]. Molecular graphics were obtained with the program Moldraw [25,26].
3. RESULTS AND DISCUSSION
The catalytic cycle starts from the active species ylide/ carbene thiamin in the 4’-amino tautomeric form (Scheme 3).
As a preliminary step to the catalytic cycle, a proton is transferred from the C2 of the N-alkyl thiazolium ring in structure 1 to the 4’-imino group of the 1’,4’-iminopyrimidine (Figure 1) with formation of the active ylide/ carbene species 2. The need for a computed barrier for this process was pointed out by Schiøtt [8]. The step is exothermic by 10.40 kcal·mol–1, with a small barrier of 1.79 kcal·mol–1. In order to form the active species, the imino-ThDP cation is made to interact with the carboxylate of model Glu50 (acetate anion), resulting in the proton transfer from N1’ to the carboxylate in structure 1, with a dipole moment of 6.4 debye. In the following transition structure (TS-12), the proton bound to C2 of the N-alkyl thiazolium ring in structure 1 is transferred to the 4’-imino group of the 1’,4’-iminopyrimidine, with formation of the active ylide/carbene species 2 (Figure 2). This result is in agreement with the study of Schiøtt [19], who concluded that the energetically favored generation of the ylide/carbene is direct, without the intervention of hydrogen-bonding amino acid residues. Since the catalytic cycle no longer involves structure 1, the energy profile will be based on the potential energy of species 2, conventionally placed at 0.00 kcal·mol–1. On this scale, minimum 1 lies at 10.40 kcal·mol–1 and TS-12 at 12.19 kcal·mol–1, respectively. The following discussion will be based on two types of potential energy differences, namely energies with respect to reactant cluster 2 (ΔU in Figures 1-7), and energy barriers with respect to the previous minimum in the catalytic cycle (ΔUth). This distinction follows from the short equilibration time for the energy redistribution among vibrational modes in the substrate given by the interaction of the reacting species with the active site. In other words, the vibrational kinetic energy from an exothermic step cannot fully contribute to overcoming the following potential energy barrier, since the excess reaction energy is promptly transferred to the active site through dynamical coupling. Consequently, a negative potential energy barrier (if computed with respect to minimum 2) does not necessarily imply a fast kinetic step, and we also correctly report the same barrier calculated with respect to the previous


Figure 1. Cluster of zwitterionic thiamin with substrate pyruvic acid and acetic acid as a model of Glu50 (1). Transition structure for the proton transfer from the C-H of the thiazolium ring to the exocyclic imino group of the pyrimidine ring (TS-12). Energies are calculated at the B3LYP 6-31G (d, p) level of theory.
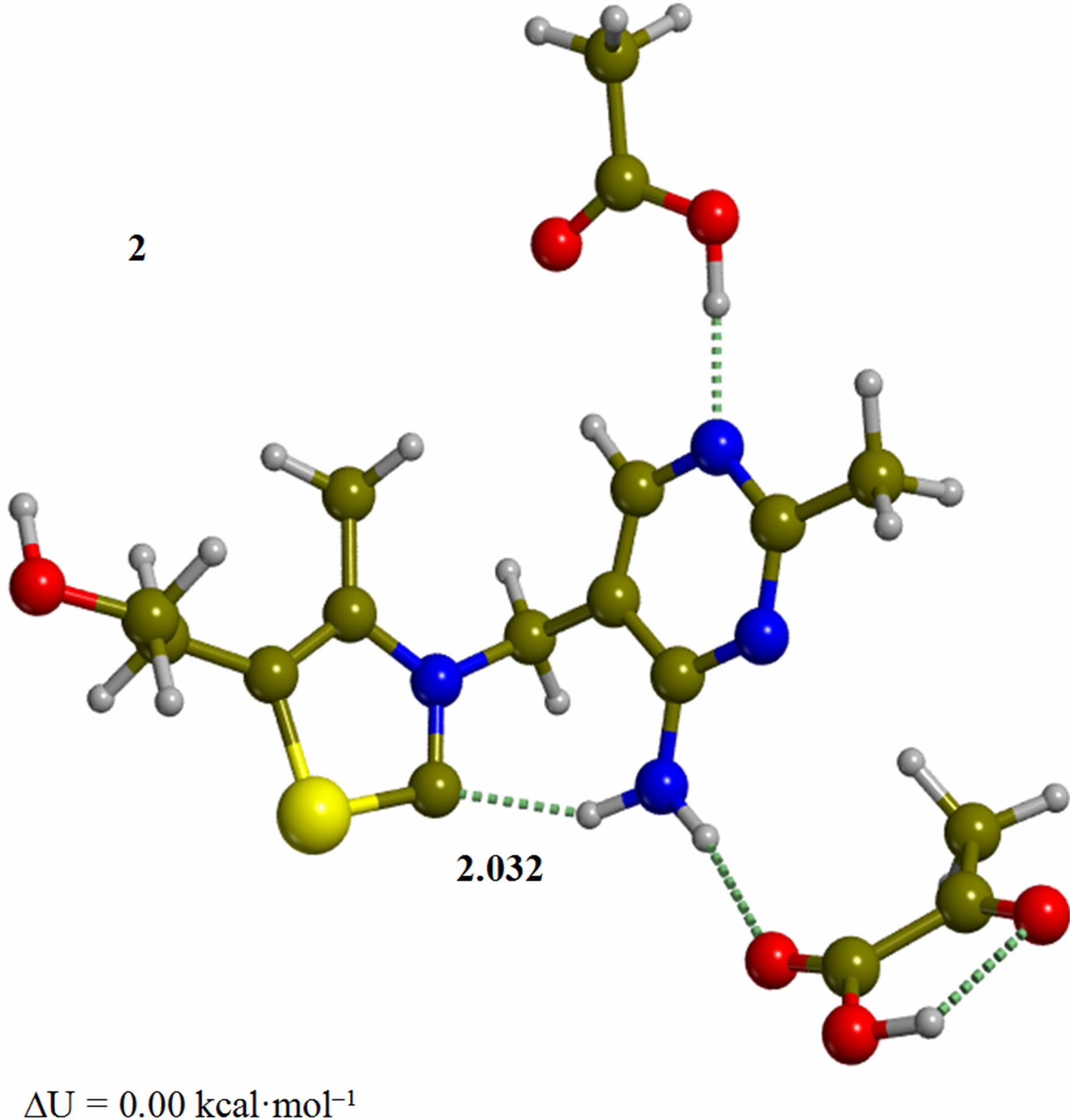
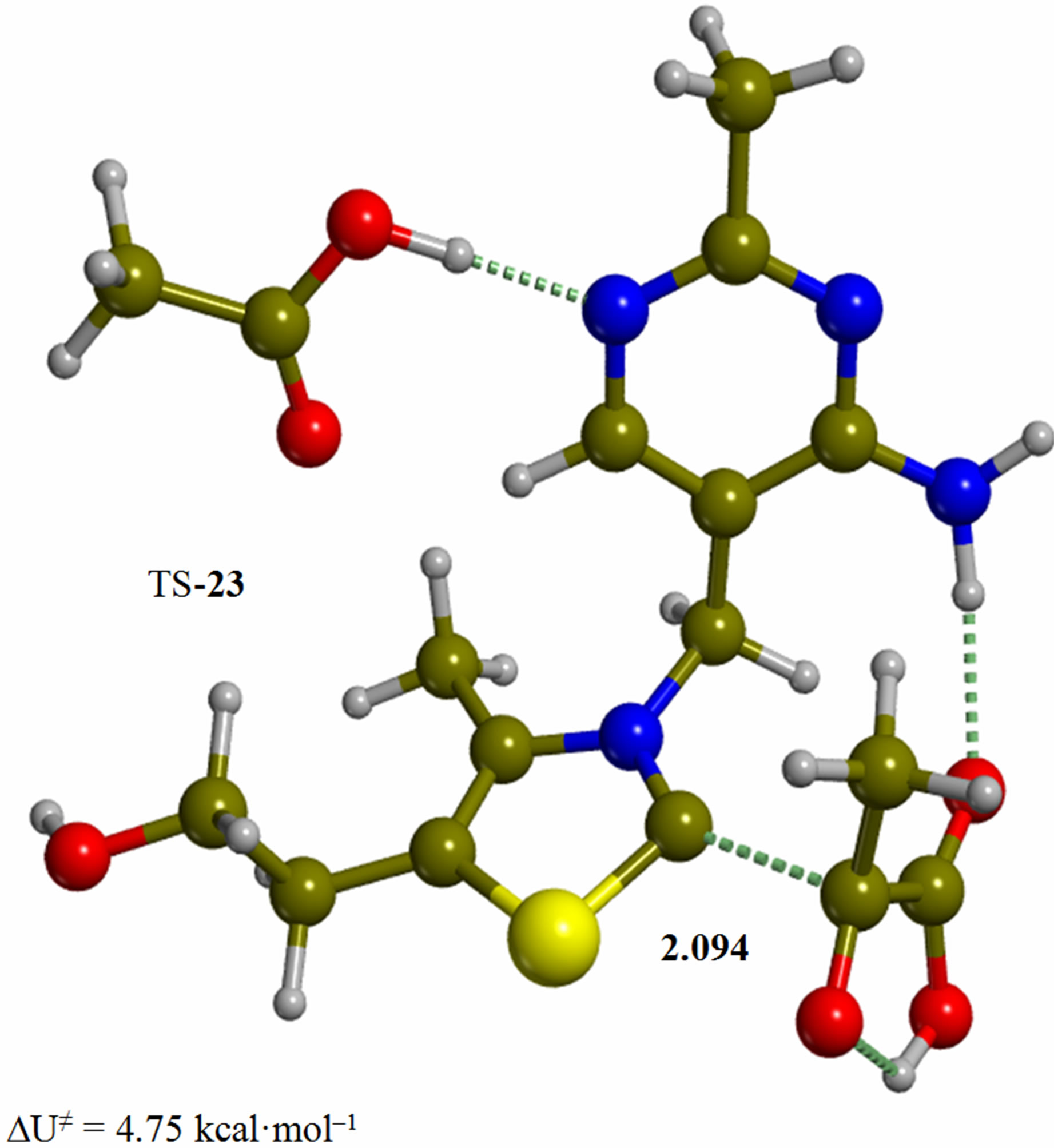
Figure 2. Cluster of the ylide/carbene thiamin in the 4’-amino tautomeric form with substrate pyruvic acid and acetic acid (2). The corresponding transition structure for addition of the C2 to the carbonyl group of pyruvic acid (TS-23). Energies are calculated at the B3LYP 6-31G (d, p) level of theory.


Figure 3. Tetrahedral adduct of the 4’-amino tautomer of thiamin to pyruvic acid (3). The corresponding transition structure for decarboxylation (TS-34). Energies are calculated at the B3LYP 6-31G (d, p) level of theory.
minimum. In structure 2 the ylide/carbene moiety has the necessary nucleophilicity at C2 to attack the carbonyl group in the pyruvic acid. In fact, a Mulliken population analysis on 2 shows that the charges on C2, S1, and N3 are –0.14, 0.22, –0.41, respectively. The corresponding dipole moment of 2 is 2.4 debye. In both structures 1 and 2, the “V” conformation is retained by the full geometry optimization. In this light, we considered all the subsequent mechanistic steps to proceed with the only participation of ThDP. This result is in line with the previous interpretation of enzyme catalysis that individuates the role of the protein to be dynamic in nature [27].


Figure 4. Enamine intermediate adduct of the 4’-amino tautomer of thiamin (4). The corresponding transition structure for proton transfer from the amino group of the pyrimidine ring to the enol carbon (TS-45). Energies are calculated at the B3LYP 6-31G (d, p) level of theory.


Figure 5. Imino form of the hydroxyethyl intermediate (5). The corresponding transition structure for proton transfer from the hydroxyethyl group to the exocyclic 4’-imino group of the pyrimidine ring (TS-56). Energies are calculated at the B3LYP 6-31G (d, p) level of theory.
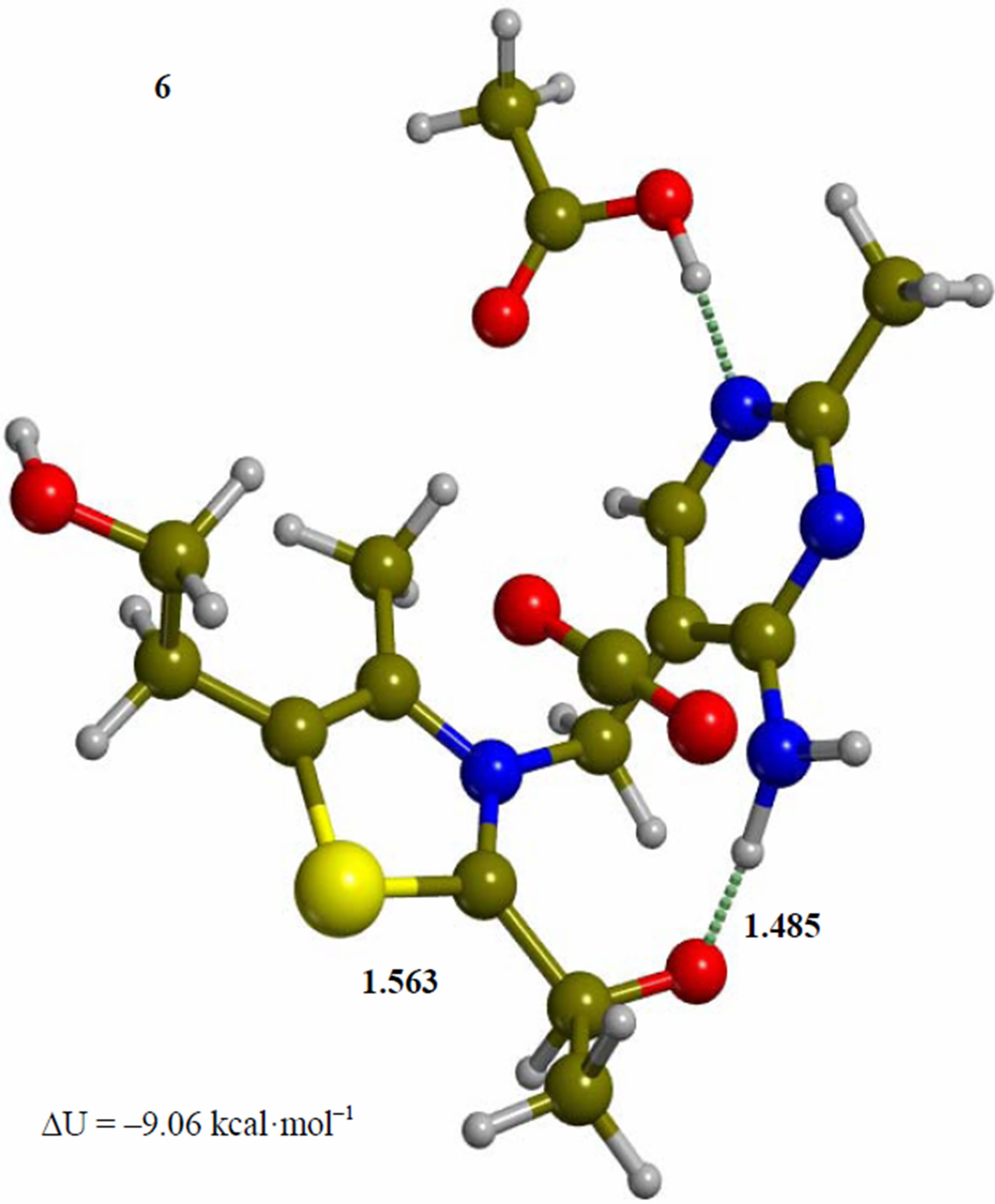
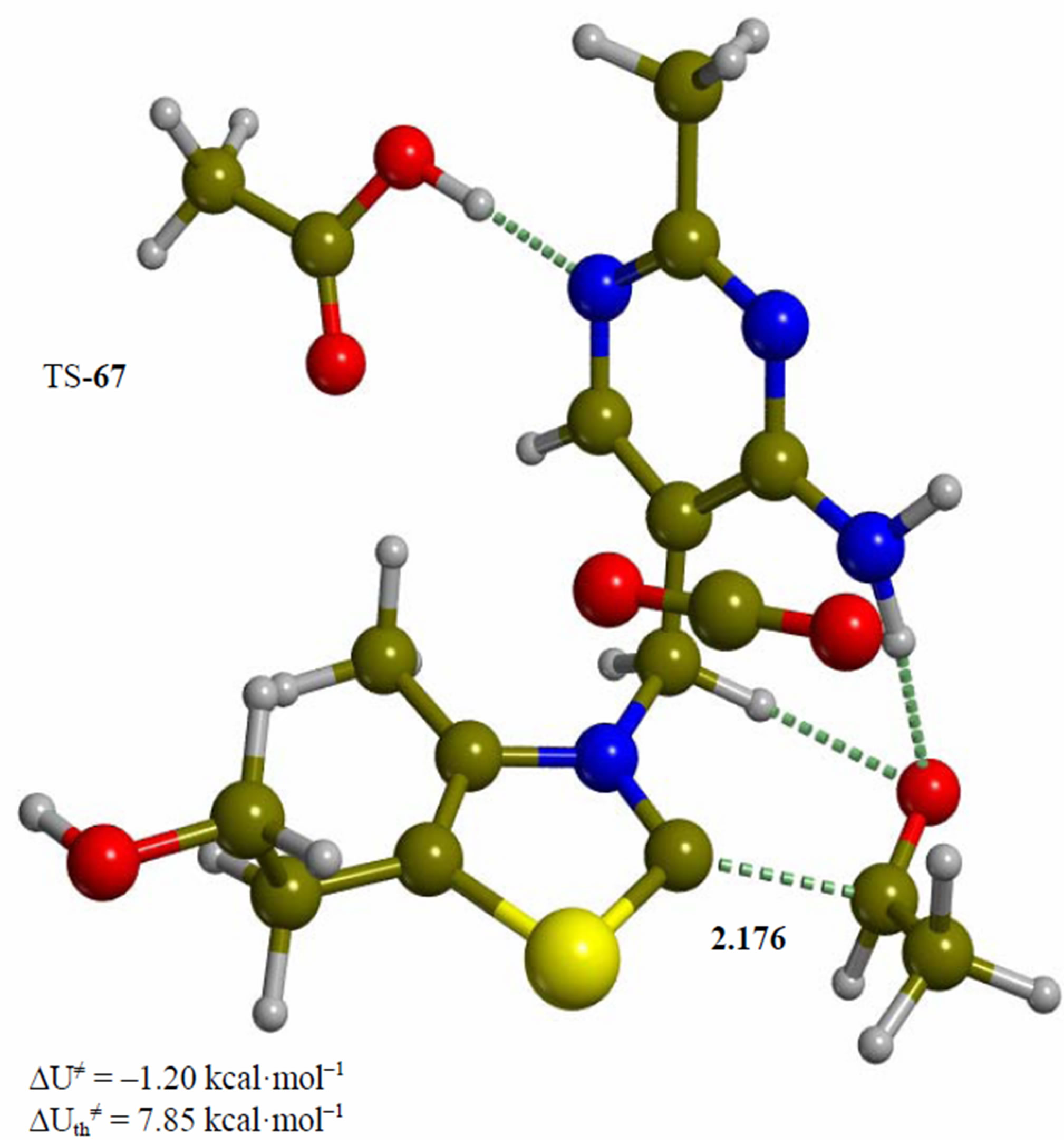
Figure 6. Intermediate acetaldehyde adduct of the 4’-amino tautomer of thiamin (6). The corresponding transition structure for product release (TS-67). Energies are calculated at the B3LYP 6-31G (d, p) level of theory.
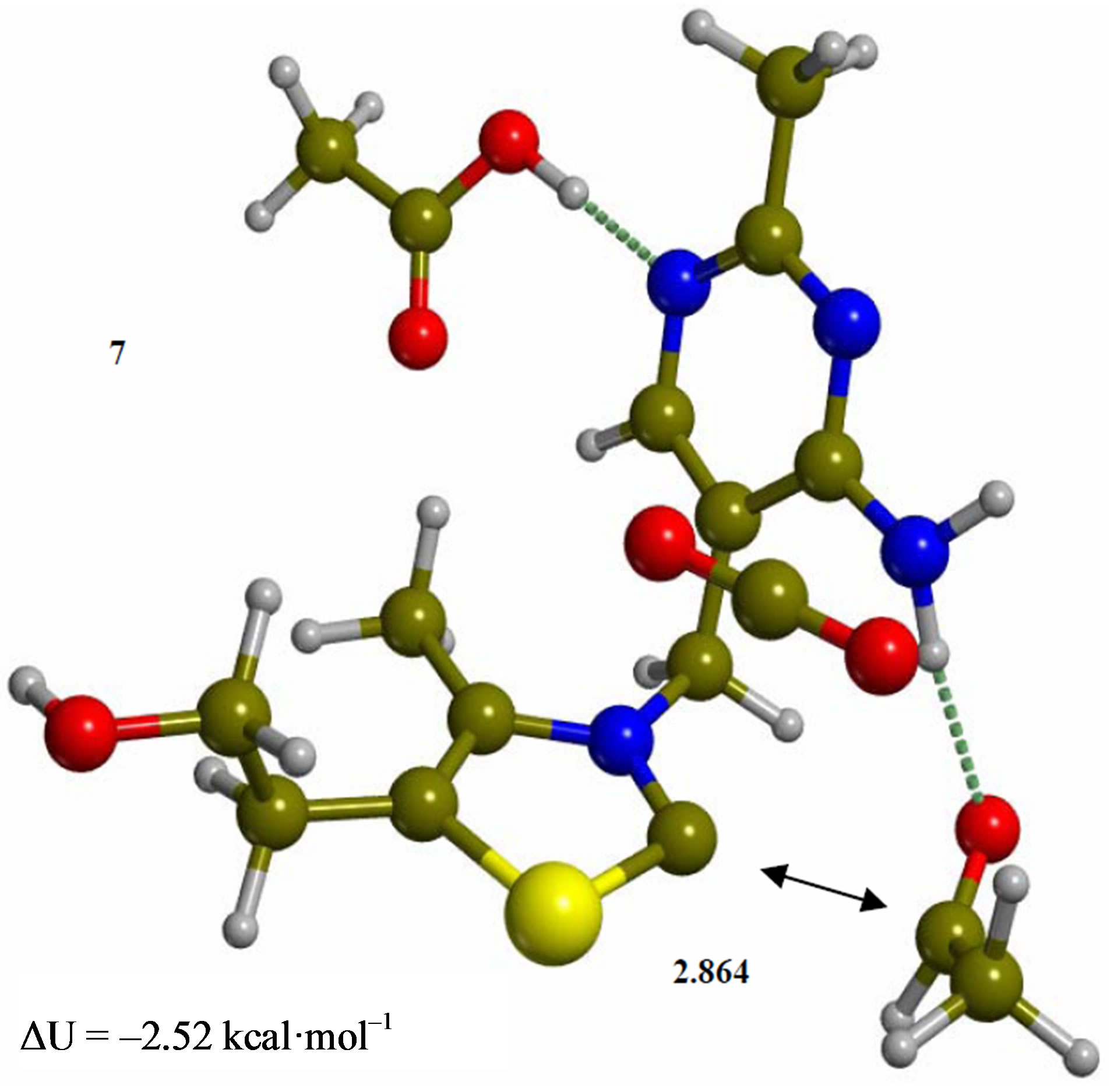
Figure 7. Complex of product acetaldehyde with the ylide/ carbene thiamin in the 4’-amino tautomeric form (7). Energies are calculated at the B3LYP 6-31G (d, p) level of theory.
Since the individual kinetic steps are slower than energy thermalization of the reaction intermediates, we chose to discuss the barriers defined as potential energy differences with respect to the previous minimum (ΔUth). The nucleophilic ylide/carbene 2 attacks the carbonyl group of pyruvic acid in TS-23 (Figure 2), with a barrier of 4.75 kcal·mol–1, to afford LThDP 3 (Figure 3), 15.31 kcal·mol–1 below the energy of 2. The reaction eigenvector of TS-23 displays the formation of the bond between C2 and the carbonyl at 2.094 Å, with a concerted proton transfer from the carboxylic group of pyruvic acid to the carbonyl oxygen. Consequently, the carboxylate group of the pyruvate in structure 3 bears a negative charge leading to a strong hydrogen bond at 1.878 Å between the carboxylate oxygen and the proximal hydrogen of the N4’ imine group (Figure 3). Structure 3 decarboxylates bringing the C-C bond from the equilibrium distance of 1.517 Å to 2.297 Å in TS-34 (Figure 3), with a thermal barrier of 10.82 kcal·mol–1. In enamine 4 (Figure 4), 12.70 kcal·mol–1 below the energy of structure 2, the double bond between C2 and the exocyclic carbon of the enol substrate is exposed to the acidic hydrogen of the N4’ imine group. TS-45 (Figure 4), with a thermal barrier of 20.55 kcal·mol–1, depicts the proton transfer from the 4’-aminopyrimidine to the enol exocyclic carbon atom, and it represents the rate-determining step of the whole mechanism, as suggested by Kluger [28]. Coexisting kinetic isotope effects at both the carbonyl carbon of pyruvate and the exocyclic 4’ nitrogen of ThDP may confirm this hypothesis [29]. The transferring proton exhibits comparable distances from the two heavy atoms (1.363 Å from the N4’ imine nitrogen and 1.336 Å from the enol carbon). Structure 5 (Figure 5) is a zwitterion with the major contribution to the positive end of the dipole (7.6 debye) on S1 (0.35 charge from the Mulliken population analysis). The negative end of the dipole rests on the pyrimidine N1’, with a charge of –0.60. In minimum 5, the 4’-iminopyrimidine moiety with its basic nitrogen atom is restored, ready to accept a proton this time from the OH group in TS-56 (Figure 5) to afford the 4’-aminopyrimidine 6 with a thermal barrier of only 1.08 kcal·mol–1. Structure 6 (Figure 6) exhibits the acetaldehyde moiety of the final product in the form of an adduct with the ylide/carbene at -9.06 kcal·mol–1 from reactant 2. The transition structure TS-67 gives the final product 7 (Figure 7), i.e. a complex of the ylide/carbene with product acetaldehyde, with a thermal barrier of 7.85 kcal·mol–1. In structure TS-67 the bond between C2 and the carbonyl in the substrate is elongated from the equilibrium value of 1.563 Å to 2.176 Å.
The potential energy profile of the mechanistic cycle is summarized in Figure 8, where the energies relative to the reactant 2 are reported in black, and the thermal barriers in red. Tables 1 and 2 report the absolute and relative energies for the enzyme-catalyzed decarboxylation

Figure 8. Potential energy profile (kcal·mol–1) of the proposed mechanism for the catalytic cycle of PDC calculated at the B3LYP 6-31G (d, p) level of theory. The energies relative to the reactant 2 are reported in black, and the thermal barriers in red.

Table 1. Potential energy profile along the pathway for the decarboxylation of pyruvic acid by the 1’,4’-imino tautomer of thiamin with the participation of model Glu50. Energies are calculated at the B3LYP 6-31G (d, p) level of theory.

Table 2. Potential energy profile for the uncatalyzed decarboxylation of pyruvic acid in water solvent. Energies are calculated at the B3LYP 6-31G (d,p) level of theory.
of pyruvic acid and the corresponding reaction in water, respectively.
The uncatalyzed decarboxylation of pyruvic acid in water was studied at the same level of theory as the catalyzed process in order to have a reference energy profile to gauge the catalytic effect of ThDP. For this process, Kakkar reports a free energy barrier of 77.3 kcal·mol–1 for the direct decarboxylation of pyruvic acid in water solution at the DFT level [30]. In the direct mechanism the carboxylic proton of pyruvic acid is transferred to the carbonyl carbon with the immediate formation of acetaldehyde and CO2 in one step. The alternative mechanism of decarboxylation of pyruvic acid through hydroxyethylidene has been reported to be favored with respect to direct decarboxylation at the PM3 level of theory [31], but it did not afford a first-order saddle point both in the gas and condensed phase at the DFT level. The structures of the critical points along the reaction path for the uncatalyzed decarboxylation of pyruvic acid in this work are summarized in Figure 9. A first-order saddle point for the decarboxylation of the pyruvic acidwater cluster 1u could not be located, the potential energy surface being always attractive for any distance between the carbonyl carbon and the leaving CO2. The hydroxyethylidene 2u lies 52.94 kcal·mol–1 above the reagent cluster 1u, while the potential energy of the following transition structure (TS-23u) for the insertion of hydroxyethylidene into the O-H bond of a water molecule is 60.77 kcal·mol–1 above the reagent, with a thermal barrier of only 7.83 kcal·mol–1. The insertion product 3u is the hydrated form of acetaldehyde, 8.41 kcal·mol–1 below the reactant. The transition structure for the elimination of water from 3u, (TS-34u) exhibits a thermal barrier of 43.59 kcal·mol–1, leading to the final product 4u, the cluster of acetaldehyde with a water molecule and CO2, 4.39 kcal·mol–1 below the reactant. The rate-determining step for this process is clearly the loss of CO2 from reagent cluster 1u, requiring at least 52.94 kcal·mol–1, and making the rate for the uncatalyzed decarboxylation of pyruvic acid virtually negligible. Saito [32] reports an experimental decarboxylation barrier for pyruvic acid in the gas phase at 850 - 1000 K of 40.0 kcal·mol–1. The corresponding calculated barrier at the HF/6-3lG**//HF/ 3-21G level of theory is 40.8 kcal·mol–1. On the other hand, the rate of decarboxylation of α-lactylamin has been reported by Kluger to be 4.0 10–5 s–1 at pH = 7, and the rate for the conversion of pyruvate to acetaldehyde by yeast pyruvate decarboxylase is six orders of magnitude higher with respect to the nonenzymatic decarboxylation catalyzed by ThDP [28]. Based on the measured barrier for the uncatalyzed decarboxylation reaction, and an estimated barrier (derived from conventional transition state theory, using the experimental rate constant for the decarboxylation of α-lactylthiamin catalyzed by ThDP in water, and the calculated partition functions of 4 and TS-45) of 24.76 kcal·mol–1, the catalytic effect of the coenzyme amounts to 15.24 kcal·mol–1. This estimate is in reasonable agreement with the 20.55 kcal·mol–1 barrier for the rate-determining step proposed in this work. The remaining increase in rate for the full enzyme-catalyzed process with respect to the ThDP-catalyzed reaction in water (six orders of magnitude), can be ascribed to the dynamics of the coupling of the protein to the substrate [33].
4. CONCLUSIONS
1) A complete computed potential energy profile for the enzymatic decarboxylation of pyruvic acid catalyzed by a model thiamin diphosphate is proposed. The formation of the active ylide/carbene species appears to be direct.
2) The rate-determining step of the whole reaction path is the proton transfer from the N4’ imine group to the exocyclic carbon in enamine 4, with a barrier of 20.55 kcal·mol–1 relative to the preceding minimum. The estimated experimental barrier is 24.76 kcal·mol–1.
3) The proposed mechanism does not require the intervention of external groups to supply the needed acidic protons and is completely self-consistent.

Figure 9.Critical points along the reaction path for the uncatalyzed decarboxylation of pyruvic acid in water. Energies are calculated at the B3LYP 6-31G (d, p) level of theory.
4) A comparison between the catalyzed and uncatalyzed mechanisms for the decarboxylation of pyruvic acid is offered.
REFERENCES
- Jordan, F., Li, H. and Brown, A. (1999) Remarkable stabilization of zwitterionic intermediates may account for a billion-fold rate acceleration by thiamin diphosphate-dependent decarboxylases. Biochemistry, 38, 6369-6373. doi:10.1021/bi990373g
- Arjunan, P., Umland, T., Dyda, F., Swaminathan, S., Furey, W., Sax, M., Farrenkopf, B., Gao, Y., Zhang, D. and Jordan, F. (1996) Crystal structure of the thiamin diphosphate-dependent enzyme pyruvate decarboxylase from the yeast Saccharomyces cerevisiae at 2.3 Å resolution. Journal of Molecular Biology, 256, 590-600. doi:10.1006/jmbi.1996.0111
- Kluger, R. and Tittmann, K. (2008) Thiamin diphosphate catalysis: Enzymic and nonenzymic covalent intermediates. Chemical Reviews, 108, 1797-1833. doi:10.1021/cr068444m
- Tomita, I., Satou, Y., Ozawa, T. and Saito, S. (1973) Studies on the decarboxylation of pyruvate. II. Kinetic studies on the binding of thiamin pyrophosphate to pyruvate decarboxylase. Chemical and Pharmaceutical Bulletin, 21, 252-255. doi:10.1248/cpb.21.252
- Jordan, F. (2003) Current mechanistic understanding of thiamin diphosphate-dependent enzymatic reactions. Natural Product Reports, 20, 184-201. doi:10.1039/b111348h
- Alvarez, F.J., Ermer, J., Hübner, G., Schellenberger, A. and Schowen, R.L. (1991) Catalytic power of pyruvate decarboxylase. Rate-limiting events and microscopic rate constants from primary carbon and secondary hydrogen isotope effects. Journal of the American Chemical Society, 113, 8402-8409. doi:10.1021/ja00022a030
- Bell, P., Hoyt, K. and Shabangi, M. (2006) The electrochemical investigation of the catalytic power of pyruvate decarboxylase and its coenzyme. Bioelectrochemistry, 68, 171-174. doi:10.1016/j.bioelechem.2005.06.004
- Lie, M.A., Celik, L., Jørgensen, K.A. and Schiøtt, B. (2005) Cofactor activation and substrate binding in pyruvate decarboxylase. Insights into the reaction mechanism from molecular dynamics simulations. Biochemistry, 44, 14792-14806. doi:10.1021/bi051134y
- Turano, A., Furey, W., Pletcher, J., Sax, M., Pike, D. and Kluger, R. (1982) Synthesis and crystal structure of an analogue of 2-(α-lactyl)thiamin, racemic methyl 2-hydroxy-2-(2-thiamin)ethylphosphonate chloride trihydrate. A conformation for a least-motion, maximum-overlap mechanism for thiamin catalysis. Journal of the American Chemical Society, 104, 3089-3095. doi:10.1021/ja00375a024
- Kern, D., Kern, G., Neef, H., Tittmann, K., KillenbergJabs, M., Wikner, C., Schneider, G. and Hübner, G. (1997) How thiamine diphosphate is activated in enzymes. Science, 275, 67-70. doi:10.1126/science.275.5296.67
- Schellenberger, A., Hübner, G. and Neef, H. (1997) Cofactor designing in functional analysis of thiamin diphosphate enzymes. Methods in Enzymology, 279, 131-146. doi:10.1016/S0076-6879(97)79017-7
- Jordan, F., Nemeria, N.S., Zhang, S., Yan, Y., Arjunan, P. and Furey, W. (2003) Dual catalytic apparatus of the thiamin diphosphate coenzyme: Acid-base via the 1’,4’-iminopyrimidine tautomer along with its electrophilic role. Journal of the American Chemical Society, 125, 12732-12738. doi:10.1021/ja0346126
- Nemeria, N., Baykal, A., Joseph, E., Zhang, S., Yan, Y., Furey, W. and Jordan, F. (2004) Tetrahedral intermediates in thiamin diphosphate-dependent decarboxylations exist as a 1’,4’-imino tautomeric form of the coenzyme, unlike the Michaelis complex or the free coenzyme. Biochemistry, 43, 6565-6575. doi:10.1021/bi049549r
- Tittmann, K., Golbik, R., Uhlemann, K., Khailova, L., Schneider, G., Patel, M., Jordan, F., Chipman, D.M., Duggleby, R.G. and Hübner, G. (2003) NMR analysis of covalent intermediates in thiamin diphosphate enzymes. Biochemistry, 42, 7885-7891. doi:10.1021/bi034465o
- Chen, L., Yuan, Y. and Huskey, W.P. (2004) Transitionstate responses to amino acid perturbations in yeast pyruvate decarboxylase: A carbon kinetic isotope effect study. Journal of Physical Organic Chemistry, 17, 572-578. doi:10.1002/poc.774
- Schütz, A., Golbik, R., König, S., Hübner, G. and Tittmann, K. (2005) Intermediates and transition states in thiamin diphosphate-dependent decarboxylases. A kinetic and NMR study on wild-type indolepyruvate decarboxylase and variants using indolepyruvate, benzoylformate, and pyruvate as substrates. Biochemistry, 44, 6164-6179. doi:10.1021/bi0473354
- Wang, J., Dong, H., Li, S. and He, H. (2005) Theoretical study toward understanding the catalytic mechanism of pyruvate decarboxylase. The Journal of Physical Chemistry B, 109, 18664-18672. doi:10.1021/jp052802s
- Friedmann, R., Tittmann, K., Golbik, R. and Hübner, G. (2004) DFT studies on key intermediates in thiamin catalysis. International Journal of Quantum Chemistry, 99, 109-114. doi:10.1002/qua.20132
- Lie, M.A. and Schiøtt, B. (2008) A DFT study of solvation effects on the tautomeric equilibrium and catalytic ylide generation of thiamin models. Journal of Computational Chemistry, 29, 1037-1047. doi:10.1002/jcc.20860
- Frisch, M.J., Trucks, G.W., Schlegel, H.B., et al. (2004) Gaussian 03, revision E. 01, Gaussian Inc., Wallingford CT.
- Peng, C., Ayala, P.Y., Schlegel, H.B. and Frisch, M.J. (1996) Using redundant internal coordinates to optimize equilibrium geometries and transition states. Journal of Computational Chemistry, 17, 49-56. doi:10.1002/(SICI)1096-987X(19960115)17:1<49::AID-JCC5>3.0.CO;2-0
- Becke, A.D. (1993) Density-functional thermochemistry. III. The role of exact exchange. The Journal of Chemical Physics, 98, 5648-5652. doi:10.1063/1.464913
- Stevens, P.J., Devlin, F.J., Chablowski, C.F., and Frisch, M.J. (1994) Ab initio calculation of vibrational absorption and circular dichroism spectra using density functional force fields. The Journal of Physical Chemistry, 80, 11623- 11627. doi:10.1021/j100096a001
- McQuarrie, D.A. (1973) Statistical thermodynamics. University Science Books, Mill Valley.
- Ugliengo, P., Viterbo, D. and Chiari, G. (1993) MOLDRAW: Molecular graphics on a personal computer. Zeitschrift für Kristallographie, 207, 9-23. doi:10.1524/zkri.1993.207.Part-1.9
- Ugliengo, P. (2006) MOLDRAW: A program to display and manipulate molecular and crystal structures. http://www.moldraw.unito.it
- Canepa, C. (2003) Rates of catalyzed processes in enzymes and other cooperative media. The Journal of Physical Chemistry B, 107, 4437-4443. doi:10.1021/jp0276698
- Kluger, R., Chin, J. and Smyth, T. (1981) Thiamin-catalyzed decarboxylation of pyruvate. Synthesis and reactivity analysis of the central, elusive intermediate, α-lactylthiamin. Journal of the American Chemical Society, 103, 884-888. doi:10.1021/ja00394a027
- Abell, L.M. and O’Leary, M.H. (1988) Nitrogen isotope effects on glutamate decarboxylase from Escherichia coli. Biochemistry, 27, 3325-3330. doi:10.1021/bi00409a031
- Kakkar, R., Pathaka, M. and Gahlot, P. (2008) Effect of aqueous solvation on the structures of pyruvic acid isomers and their reactions in solution: A computational study. Journal of Physical Organic Chemistry, 21, 23-29. doi:10.1002/poc.1270
- Kakkar, R., Chadha, P. and Verma, D. (2003) Structure and unimolecular decomposition pathways of pyruvic acid. Internet Electronic Conference of Molecular Design, Biochemistry Press. http://www.biochempress.com
- Saito, K., Sasaki, G., Okada, K. and Tanaka, S. (1994) Unimolecular decomposition of pyruvic acid: An experimental and theoretical study. The Journal of Physical Chemistry, 98, 3756-3761. doi:10.1021/j100065a034
- Canepa, C. (2011) On the curvature in logarithmic plots of rate coefficients for chemical reactions. Chemistry Central Journal, 5, 22. doi:10.1186/1752-153X-5-22
Abbreviations:
PDC = pyruvate decarboxylase; ThDP = thiamin diphosphate; LThDP(-) = 2-lactyl-ThDP; HEThDP(-) = 2-(1-hydroxyethyl)l-ThDP.

