Natural Science
Vol.4 No.7(2012), Article ID:20783,8 pages DOI:10.4236/ns.2012.47065
Electromagnetic nature of nuclear forces and the toroid structure of the helion and the alpha particle
![]()
Plovdiv University “P. Hilendarski”, Plovdiv, Bulgaria; kolikov@uni-plovdiv.bg
Received 20 May 2012; revised 18 June 2012; accepted 2 July 2012
Keywords: Helion; Alpha particle; Strong interaction; Potential binding energy; Electrostatic interaction
ABSTRACT
In the present paper, we consider the nucleons in the helium-3 and helium-4 nuclei as tori. These tori rotate with constant angular velocity around an axis, which is perpendicular to the rotation plane and passes through the centre of mass of the nuclei. Based on exact analytical expressions for the electrostatic interaction between two spheres with arbitrary radii and charges derived by us recently, we find that the well-known potential binding energy for the helion and for the alpha particle is of electromagnetic character. Using the above mentioned formulae, we find the interaction force in the nuclei under consideration. Our toroid model recovers the basic experimental results not only for the binding energy, but also for the stability, radii, spins and the magnetic moments of the helion and the alpha particle.
1. INTRODUCTION
There are two basic models in the theory of elementary particles: the standard model [1-3] and the helicon model [4-7].
In [8] and [9] the toroid model of nucleons has been proposed, which is in certain contradiction with the standard model, however in perfect agreement with the helicon model.
Every nucleon is modelled with an imaginary torus, which rotates with constant angular velocity around an axis z passing through its mass centre (the geometric centre) o and perpendicular to the rotation plane of its central circle. From quantum mechanical point of view, the nucleon is not a localized object in configuration space. Therefore, our model is valid in a formal heuristic sense a la Niels Bohr similar to his model for the electron in the hydrogen atom, with which he obtained good results for its spectrum within the framework of the old quantum mechanics.
Additional reasoning to consider the nucleons as spatially extended objects is the fact that they are located close to each other in the atomic nuclei. Thus, we assume that they are tori and their electric charge can be redistributed. Essentially, this idea does not contradict to the quark substructure model of nucleons, and it enables us to determine the electrostatic interaction between them. Based on the exact analytical expressions for the electrostatic interaction between two charged conducting spheres with arbitrary radii and charges derived for the first time in [10], we conclude in [8] that strong interactions are electromagnetic in nature.
In [9], we ascertain that the experimentally determined potential binding energy between nucleons in the deuteron and triton can be obtained taking into account the electrostatic interaction only. To do that, the values of the experimentally known radii, and masses of the nucleons and the corresponding nuclei have been utilized. In [9], the volume and the mass density of nucleons, as well as their interaction force in the deuteron and the triton have been calculated—important results in nuclear physics presented for the first time.
Applying the method developed in [8,9], we calculate in the present paper the potential energy and the interaction force between the nucleons in the helium-3 and helium-4 nuclei. Basic experimentally measured characteristics such as stability, spin, radius and magnetic moment of the helion and the alpha particle are also explained.
According to R. Feynman’s conjecture at distances less than 10−15 m either Coulomb’s law is not valid, or electrons and protons cannot be considered as point-like particles [11]. In accordance with this conjecture, we assume that the distance within the corresponding protonneutron pairs is less 10−15 m.
2. TOROID MODEL OF NUCLEONS
In [8,9] the nucleons are modeled as tori. Moreover, we assume that they rotate with constant angular velocity around an axis z passing through their mass (geometric) centre o and perpendicular to the rotation plane of their central circle (Figure 1).
Next, we study the system consisting of a proton and a neutron and determine the electrostatic interaction between them.
The tori corresponding to the proton and the neutron are denoted by 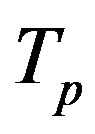 and
and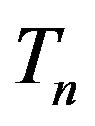 , while their centres are denoted by
, while their centres are denoted by 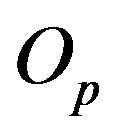 and
and , respectively. We assume that the central circles of
, respectively. We assume that the central circles of  and
and  lie in parallel or merging planes and rotate in the same or opposite direction with the same angular velocity
lie in parallel or merging planes and rotate in the same or opposite direction with the same angular velocity 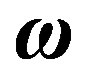 around the line z, which passes through
around the line z, which passes through 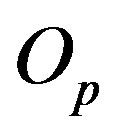 and
and  being perpendicular to the rotation plane. Then, if
being perpendicular to the rotation plane. Then, if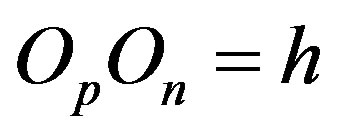 , it follows that
, it follows that  (Figure 2).
(Figure 2).
Let 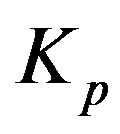 and
and  be the centres of the forming circles of the tori
be the centres of the forming circles of the tori  and
and , respectively, and
, respectively, and 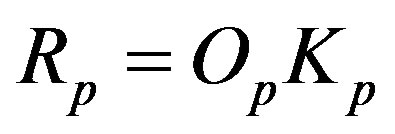 ,
,  be the radii of the central circles of
be the radii of the central circles of 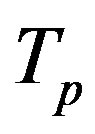 and
and . We assume that the distance between
. We assume that the distance between  and
and  is
is 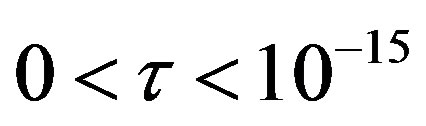 m.
m.
According to the available experimental data the proton radius  is not greater than the neutron radius
is not greater than the neutron radius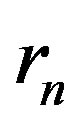 . That is why we must have
. That is why we must have .
.
Let  and
and 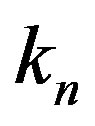 be the radii of the forming circles
be the radii of the forming circles  and
and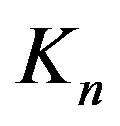 , respectively. It is clear that
, respectively. It is clear that  and
and . Moreover,
. Moreover,
 and
and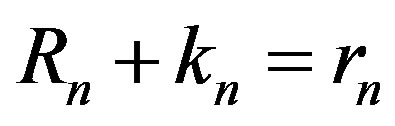 ,(1)
,(1)
where  and
and 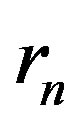 are the radii of the proton and the neutron in the configuration shown in Figure 2. It is worthwhile to note that in some nuclei
are the radii of the proton and the neutron in the configuration shown in Figure 2. It is worthwhile to note that in some nuclei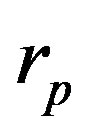 ,
,  ,
, 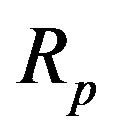 and
and ,
,  ,
, 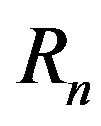 may take different values.
may take different values.
Since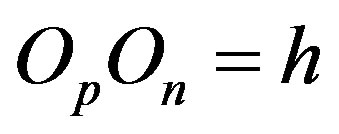 , simple geometric consideration yields
, simple geometric consideration yields
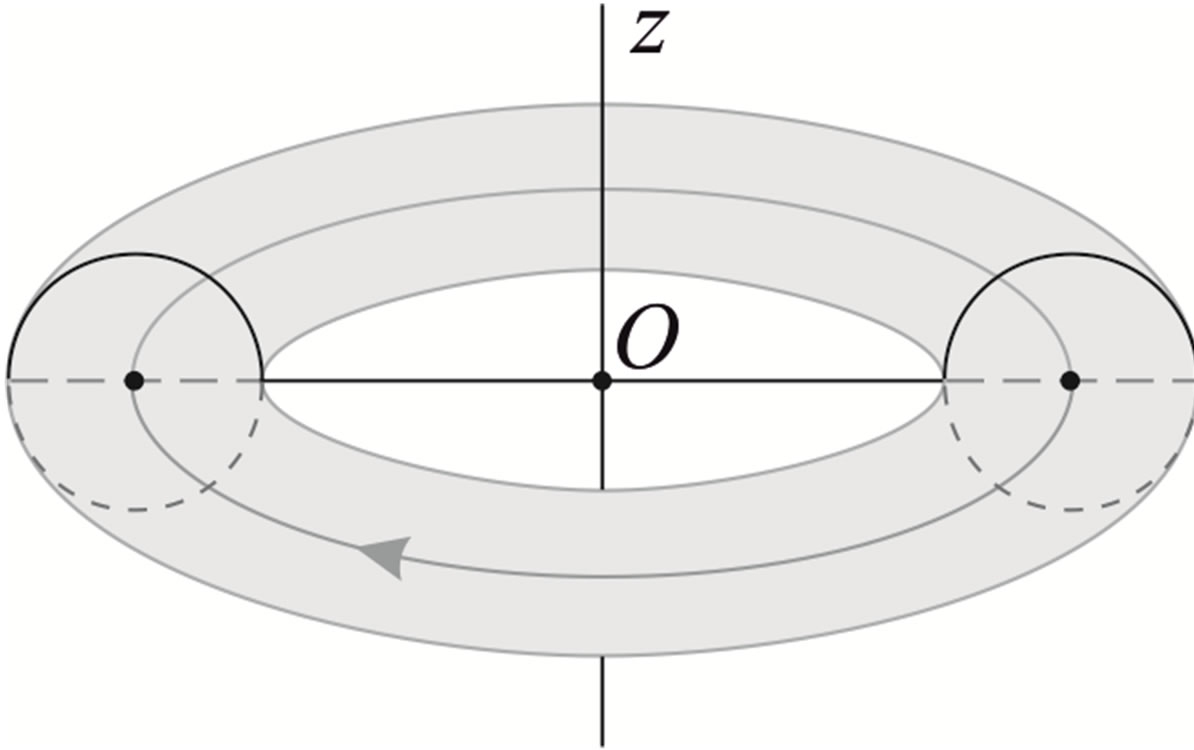
Figure 1. Toroid model of a nucleon.

Figure 2. Cross section of the system containing a proton and a neutron.
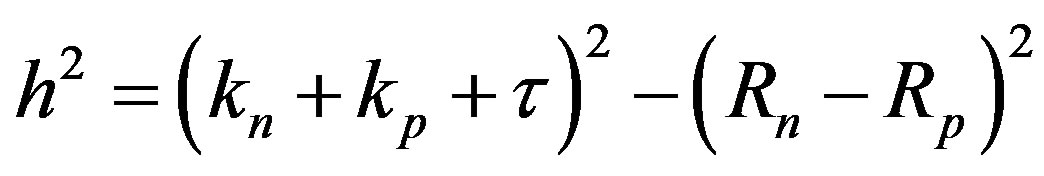 . (2)
. (2)
Obviously,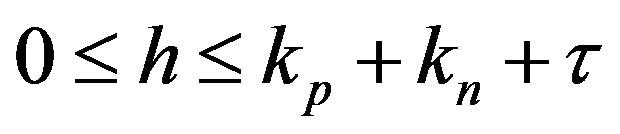 .
.
We assume that the mass and number densities of the proton and the neutron are equal, that is . If
. If 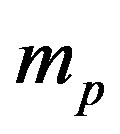 and
and  are the masses of
are the masses of 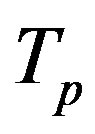 and
and , then
, then
 and
and .(3)
.(3)
According to [12], the volumes of the tori 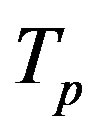 and
and  are
are 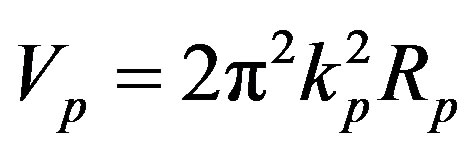 and
and , respectively. Therefore, from
, respectively. Therefore, from 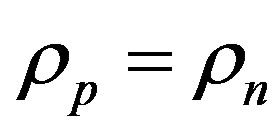 and from Eq.3 it follows that
and from Eq.3 it follows that
 . s are experimentally (4)
. s are experimentally (4)
Eqs.3 and 4 contain the proton and the neutron mass whose values are experimentally known and can be readily substituted.
Let he radius of the of the empty part of the circle with radius equal to that of the proton . Then
. Then
 . (5)
. (5)
In order to apply the results from [10] derived for the case of spheres, we remodel the tori as in [8,9].
Due to the spherical symmetry of the proton charge [13], we can assume that all its charge  is concentrated in the geometric centre
is concentrated in the geometric centre 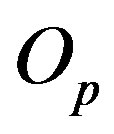 of the torus
of the torus .
.
We remodel the proton with a sphere  having the same centre
having the same centre 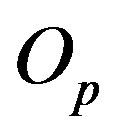 lying on the axis
lying on the axis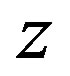 , such that its area is equal to that of the torus
, such that its area is equal to that of the torus . Moreover, the charge
. Moreover, the charge  of the sphere is spherically symmetric and it can be redistributed.
of the sphere is spherically symmetric and it can be redistributed.
According to [12] the area  of the torus
of the torus 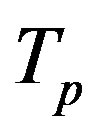 is
is
 . (6)
. (6)
Since the areas of the torus 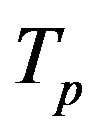 and the sphere
and the sphere 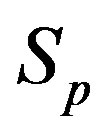 are equal, from Eq.6 it follows that the radius
are equal, from Eq.6 it follows that the radius of
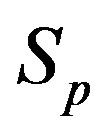 is
is
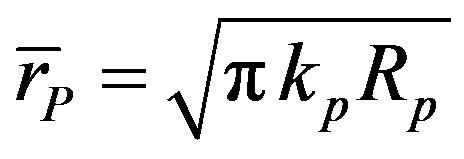 . src="10-8301676\cf42bf70-0c1d-4516-8777-95359cc6d547.jpg" width="22.8" height="28.5 " /> whose torus
. src="10-8301676\cf42bf70-0c1d-4516-8777-95359cc6d547.jpg" width="22.8" height="28.5 " /> whose torus 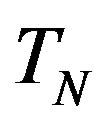 has equivalent area and the same centre
has equivalent area and the same centre . The distance
. The distance  between its surface and that of
between its surface and that of  is the same as the distance between
is the same as the distance between  and
and 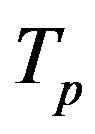 (Figure 3).
(Figure 3).
Let 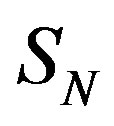 be the sphere, whose central circle is forming the torus
be the sphere, whose central circle is forming the torus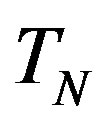 . We denote the centre of
. We denote the centre of 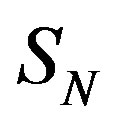 with
with 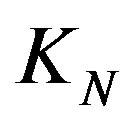 so that
so that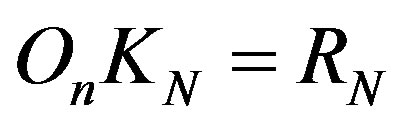 , and let
, and let  be the radius of
be the radius of . If
. If , then
, then  and
and  implies
implies , that is
, that is
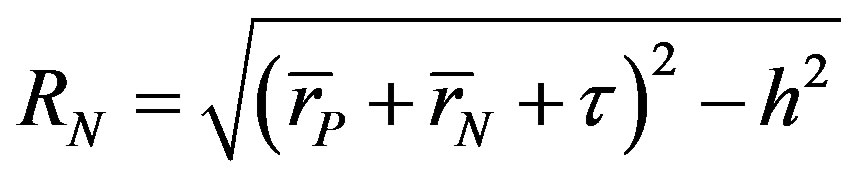 . (8)
. (8)

Figure 3. Cross section of the reduced model of the proton-neutron system.
Clearly, 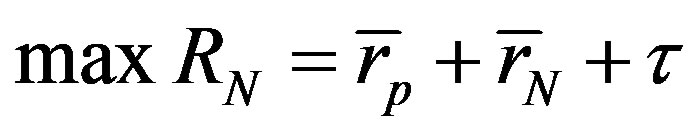 and
and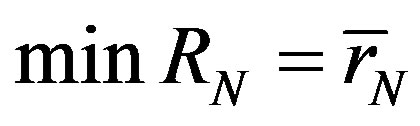 .
.
The equality of the areas  and
and  of the tori
of the tori  and
and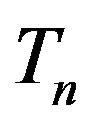 , together with Eq.6 yields
, together with Eq.6 yields
Eq.6 yields
 . d6c53ced-871f-4123-9fb1-02cf79648fda.jpg" width="12.825" height="22.8 " /> of the spheres
. d6c53ced-871f-4123-9fb1-02cf79648fda.jpg" width="12.825" height="22.8 " /> of the spheres  whose total area is equal to that of the torus
whose total area is equal to that of the torus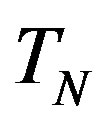 , the following relation
, the following relation 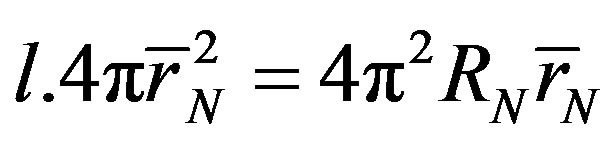 holds. Therefore
holds. Therefore
 . (10)
. (10)
Let us assume that the centre 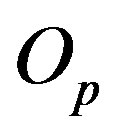 is fixed with respect to some inertial reference frame
is fixed with respect to some inertial reference frame . Next, we introduce a rigid inertial coordinate system
. Next, we introduce a rigid inertial coordinate system , which rotates with the constant angular velocity
, which rotates with the constant angular velocity 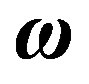 of the torus
of the torus  rotation with respect to
rotation with respect to . The point
. The point  is the centre of the coordinate system
is the centre of the coordinate system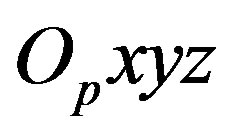 , which is firmly fixed with
, which is firmly fixed with  and the spheres
and the spheres 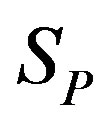 and
and 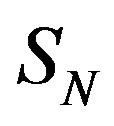 are at rest one against the other (Figure 3).
are at rest one against the other (Figure 3).
Thus, taking into account the experimentally found value for 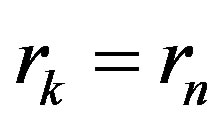 (
(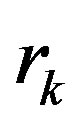 is the radius of the considering nucleus), assigning different values for
is the radius of the considering nucleus), assigning different values for 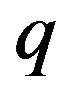 and varying
and varying  m and
m and , from Eqs.1-5 we can find
, from Eqs.1-5 we can find ,
, 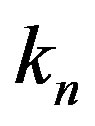 and
and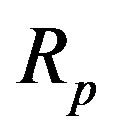 ,
,  ,
, . Combining with Eq.7 we determine the radius
. Combining with Eq.7 we determine the radius  of the sphere
of the sphere
 with equivalent area. From Eqs.8 and 9 we determine the radius
with equivalent area. From Eqs.8 and 9 we determine the radius of the forming sphere
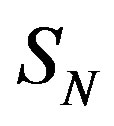 .15.425" height="29.925 " /> and taking into account ([10], Eqs.10 and 11 therein), we can determine the interaction force and taking into account ([10], Eqs.10 and 11 therein), we can determine the interaction force
.15.425" height="29.925 " /> and taking into account ([10], Eqs.10 and 11 therein), we can determine the interaction force and taking into account ([10], Eqs.10 and 11 therein), we can determine the interaction force 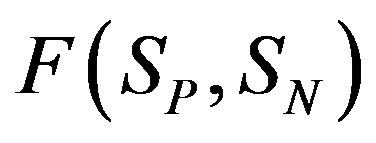 and the binding energy
and the binding energy . According to Eq.10 the binding energy
. According to Eq.10 the binding energy 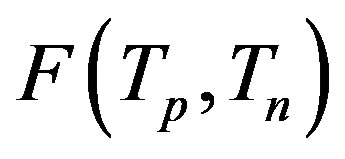 between the proton and the neutron become
between the proton and the neutron become
 (11)
(11)
Eq.11 hold because the forming spheres of the torus are located symmetrically with respect to the centre of the sphere
 .oton in a free state as the torus
.oton in a free state as the torus 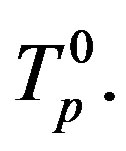 According to [14] its radius is
According to [14] its radius is 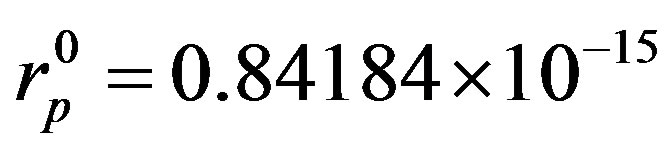 m. Let
m. Let 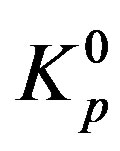 is the centre of forming circle of the torus
is the centre of forming circle of the torus 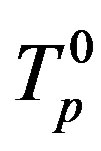 and let
and let  is the radius of this circle. Moreover,
is the radius of this circle. Moreover,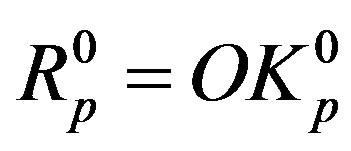 .
.
Utilizing expressions (1) and (5) for different values of the radius  of the empty part of the circle with radius
of the empty part of the circle with radius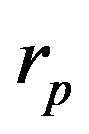 , we have calculated in [9] the quantities
, we have calculated in [9] the quantities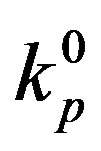 ,
, 
and the volume of the proton torus 
[12]. The mass of the proton in a free state is  kg [15]. This can be used to calculate
kg [15]. This can be used to calculate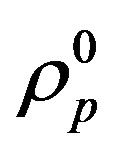 .
.
These results are depicted in Table 1 for various values of .
.
Since, the mass of the neutron  kg [15] is also known, its volume
kg [15] is also known, its volume 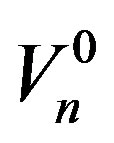 in a free state can be determined, where
in a free state can be determined, where 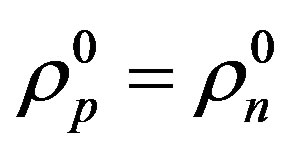 has been taken into account as already mentioned in Section 2.
has been taken into account as already mentioned in Section 2.
Due to the mass defect in the atomic nuclei, the volumes of the nucleons change. We conjecture however, that the mass densities of the proton and the neutron in all nuclei do not change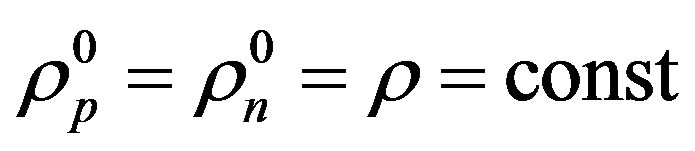 . Based on the values presented in Table 1, we ascertain the potential binding energy and calculate the interaction force in the deuteron and the triton in [9].
. Based on the values presented in Table 1, we ascertain the potential binding energy and calculate the interaction force in the deuteron and the triton in [9].
We model the deuteron as two immersed concentric tori. The inner one  corresponds to the proton, while the outer
corresponds to the proton, while the outer  corresponds to the neutron, such that the distance between
corresponds to the neutron, such that the distance between  and
and  is of the order of
is of the order of  m. In addition, we assume that the two tori rotate in the same direction with constant angular velocity
m. In addition, we assume that the two tori rotate in the same direction with constant angular velocity 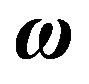 around a straight line
around a straight line  passing through their common centre and perpendicular to the rotation plane.
passing through their common centre and perpendicular to the rotation plane.
We model the triton with three tori whose central circles

Table 1. Dimensions, volume and mass density of the proton.
lie in three parallel planes. The tori  and
and  representing the neutrons are located symmetrically on both sides of the torus
representing the neutrons are located symmetrically on both sides of the torus  representing the proton. The distance between the neutron tori
representing the proton. The distance between the neutron tori ,
, 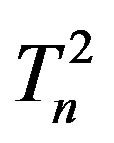 and the proton one
and the proton one  is the same and of the order of
is the same and of the order of 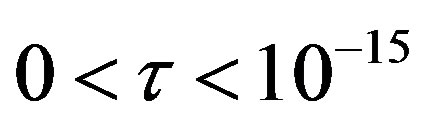 m. The tori
m. The tori 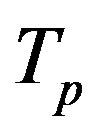 and
and 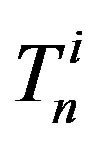
 rotate around an axis
rotate around an axis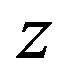 , which passes through their centres and is perpendicular to the rotation plane. The tori
, which passes through their centres and is perpendicular to the rotation plane. The tori 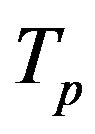 and
and 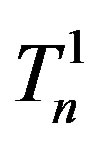 rotate with constant angular velocity
rotate with constant angular velocity  in the same direction (clockwise, for example), while
in the same direction (clockwise, for example), while  rotates with the same angular velocity in the opposite direction.
rotates with the same angular velocity in the opposite direction.
In the subsequent exposition we will model the helium-3 and the helium-4 nuclei. The nucleon disposition must comply with the principle of the minimum of potential energy. Taking into account the mass defect in atomic nuclei, the potential energy of interaction can be calculated according to the following formula [16]
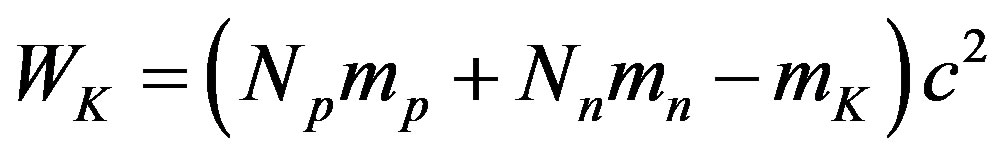 . (12)
. (12)
Here 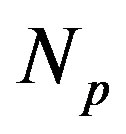 is the number of protons,
is the number of protons, 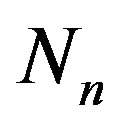 is the number of neutrons, while
is the number of neutrons, while  kg and
kg and  kg are the proton and the neutron mass, respectively [15],
kg are the proton and the neutron mass, respectively [15],  is the mass of the nucleus and
is the mass of the nucleus and 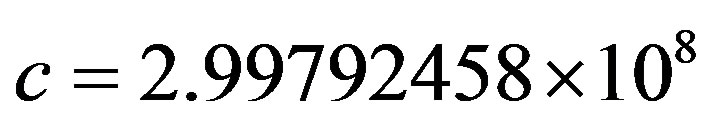 ms−1 is the speed of light in vacuum [15].
ms−1 is the speed of light in vacuum [15].
Based on the values for mass densities in Table 1, we calculate the corresponding values of  for the helion and the alpha particle, we follow the procedure described in Section 2. Finally, our results will be compared with the values obtained by virtue of Eq.12.
for the helion and the alpha particle, we follow the procedure described in Section 2. Finally, our results will be compared with the values obtained by virtue of Eq.12.
4. MODEL OF THE HELION
The helion is a mirror nucleus of the triton and therefore its structure is analogous to that of the latter [9]. It consists of one neutron 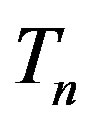 and two protons
and two protons  and
and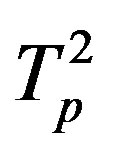 . Since the proton tori
. Since the proton tori 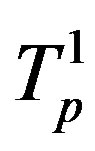 and
and 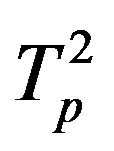 repel due to the electrostatic interaction between them, their central circles will lie in two parallel planes symmetrically located on both sides of the plane in which the central circle of the neutron torus
repel due to the electrostatic interaction between them, their central circles will lie in two parallel planes symmetrically located on both sides of the plane in which the central circle of the neutron torus 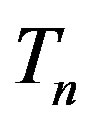 is located. In addition, the distance between the surfaces of
is located. In addition, the distance between the surfaces of ,
,  and that of
and that of  will be the same
will be the same  m (Figure 4).
m (Figure 4).
This configuration ensures symmetry with respect to the mass centre (the geometric centre) of the helion. This also implies the helion stability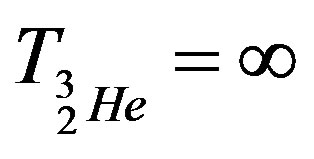 .
.
The centres  and
and 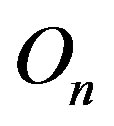 of the tori
of the tori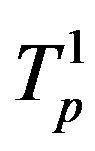 ,
, 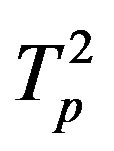 and
and , respectively lie on one axis
, respectively lie on one axis  perpendicular to their plane of rotation with
perpendicular to their plane of rotation with 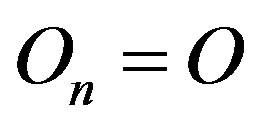 being the mass centre of the helion. The tori
being the mass centre of the helion. The tori 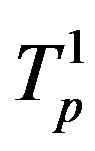 and
and  rotate with constant angular velocity
rotate with constant angular velocity  in a certain direction, while
in a certain direction, while  rotates with the same angular velocity but in the opposite direction. From here it follows directly that the
rotates with the same angular velocity but in the opposite direction. From here it follows directly that the

Figure 4. Cross section of the helion model.
spin of the helion is , which is an experimentally established fact [16].
, which is an experimentally established fact [16].
The proton rotating in an opposite direction decreases the centrifugal force, which is originated by the two nucleons rotating in the same direction. That is why the helion radius  m [17] is smaller than that of the deuteron
m [17] is smaller than that of the deuteron 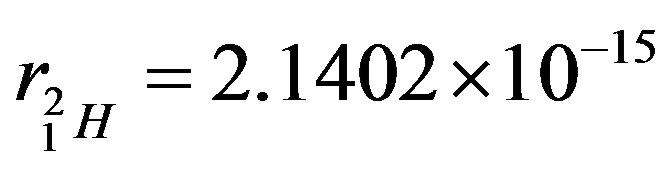 m [15].
m [15].
The magnetic moments due to the proton charges compensate each other. Thus, the magnetic moment of the helion is generated by the charge of the neutron only. As a consequence of the enlarged neutron radius as compared to that in a free state, the magnetic moment of the helion  JT−1 is greater in absolute value than the magnetic moment of the neutron
JT−1 is greater in absolute value than the magnetic moment of the neutron  JT−1, which is in agreement with the experimental data [15].
JT−1, which is in agreement with the experimental data [15].
Let 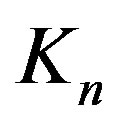 and
and 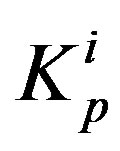 be the centres of the forming circles of
be the centres of the forming circles of 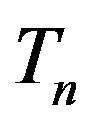 and
and , respectively with radii
, respectively with radii 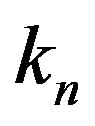 and
and 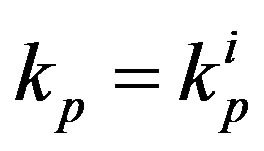
 . We introduce the notations
. We introduce the notations 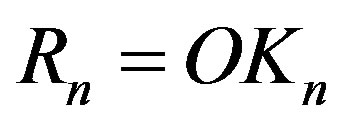 and for
and for ,
,  (Figure 4).
(Figure 4).
This means that . Since the neutron radius is equal to the radius of the helion, it follows that
. Since the neutron radius is equal to the radius of the helion, it follows that 
and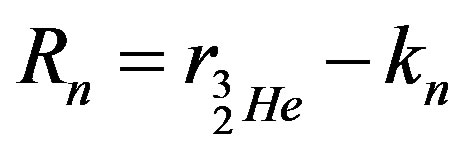 .
.
Due to the spherical symmetry of the proton charges, we can assume that their charges  C are concentrated in their geometric centres
C are concentrated in their geometric centres 
 . On these grounds we can model the protons with spheres
. On these grounds we can model the protons with spheres  having the same centres
having the same centres  and radii
and radii 
 with areas equal to the areas of
with areas equal to the areas of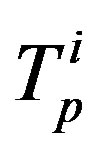 . Moreover, the charge of each
. Moreover, the charge of each  is
is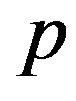 , which is spherically symmetric and can be redistributed.
, which is spherically symmetric and can be redistributed.
With  we denote the torus which is equivalent in area to
we denote the torus which is equivalent in area to 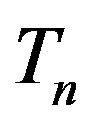 with the same centre
with the same centre . The distance between
. The distance between  and
and  is equal to the distance
is equal to the distance  between
between  and
and . Let us denote: with
. Let us denote: with  the sphere whose central circle is the forming circle of the torus
the sphere whose central circle is the forming circle of the torus ; with
; with  the center of the sphere and with
the center of the sphere and with 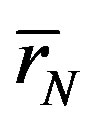 the radius of the sphere (Figure 5).
the radius of the sphere (Figure 5).
We assume that the points 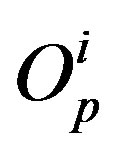 are at rest with respect to an inertial frame
are at rest with respect to an inertial frame . Let us also introduce two rigid non inertial reference frames
. Let us also introduce two rigid non inertial reference frames  and
and 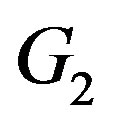 rotating with respect to
rotating with respect to  with angular velocity equal to that of the rotation of the torus
with angular velocity equal to that of the rotation of the torus .
.
The point  is the centre of the coordinate system
is the centre of the coordinate system  and is fixed firmly with the reference frame
and is fixed firmly with the reference frame 
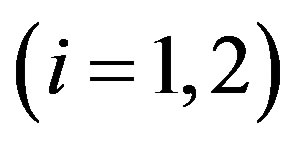 relative to which the spheres
relative to which the spheres 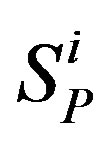 and
and 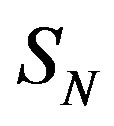 are at rest one against the other (Figure 5).
are at rest one against the other (Figure 5).
The torus  is located symmetrically with respect to the two spheres
is located symmetrically with respect to the two spheres . It suffices to analyse the electrostatic interaction between
. It suffices to analyse the electrostatic interaction between 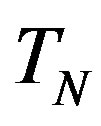 and any of the spheres. Based on the calculations presented in [8], we assume that the electrostatic interaction between the spheres
and any of the spheres. Based on the calculations presented in [8], we assume that the electrostatic interaction between the spheres  and
and 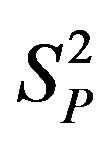 can be approximated with interaction between point-like charges
can be approximated with interaction between point-like charges ,
,  concentrated in their centres, i.e.
concentrated in their centres, i.e. 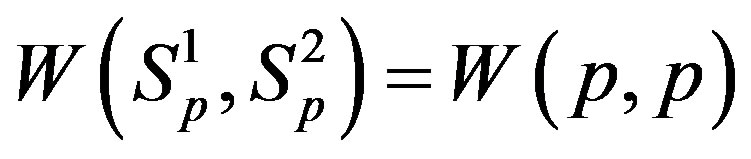 and
and . For the sake of simplicity, we assume that the distance
. For the sake of simplicity, we assume that the distance  between the surfaces of the protons
between the surfaces of the protons  and
and  is the same as the distance between
is the same as the distance between 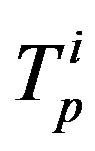 and
and , i.e.
, i.e.
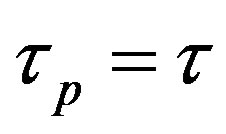 . Therefore, we must have
. Therefore, we must have  (Figure 4).
(Figure 4).
Using Eqs.1-5 from Section 2, we calculate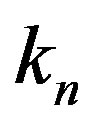 ,
, 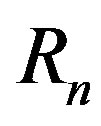 and
and ,
,  ,
, 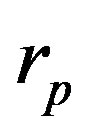 for different values of the mass density
for different values of the mass density 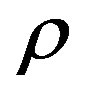 taken from Table 1 of Section 3 and different values of the distance
taken from Table 1 of Section 3 and different values of the distance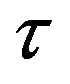 . The mass defect of the two protons and the neutron has been taken into account in Eqs.3 and 4 accordingly to the mass proportions of the nucleons. According to Eqs.7-9 we calculate
. The mass defect of the two protons and the neutron has been taken into account in Eqs.3 and 4 accordingly to the mass proportions of the nucleons. According to Eqs.7-9 we calculate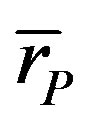 ,
,  and the distance
and the distance 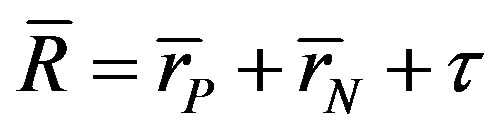 between the centers of the spheres
between the centers of the spheres  and
and .
.
The experimentally established mass of the helion is
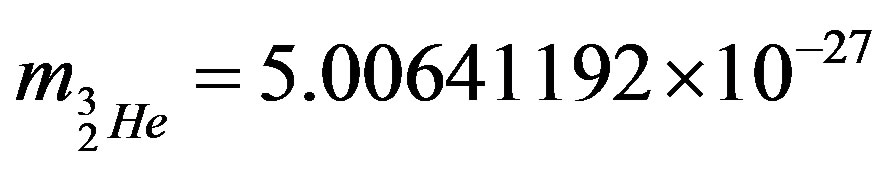 kg [15]. According to Eq.12 the binding energy of the helion is
kg [15]. According to Eq.12 the binding energy of the helion is
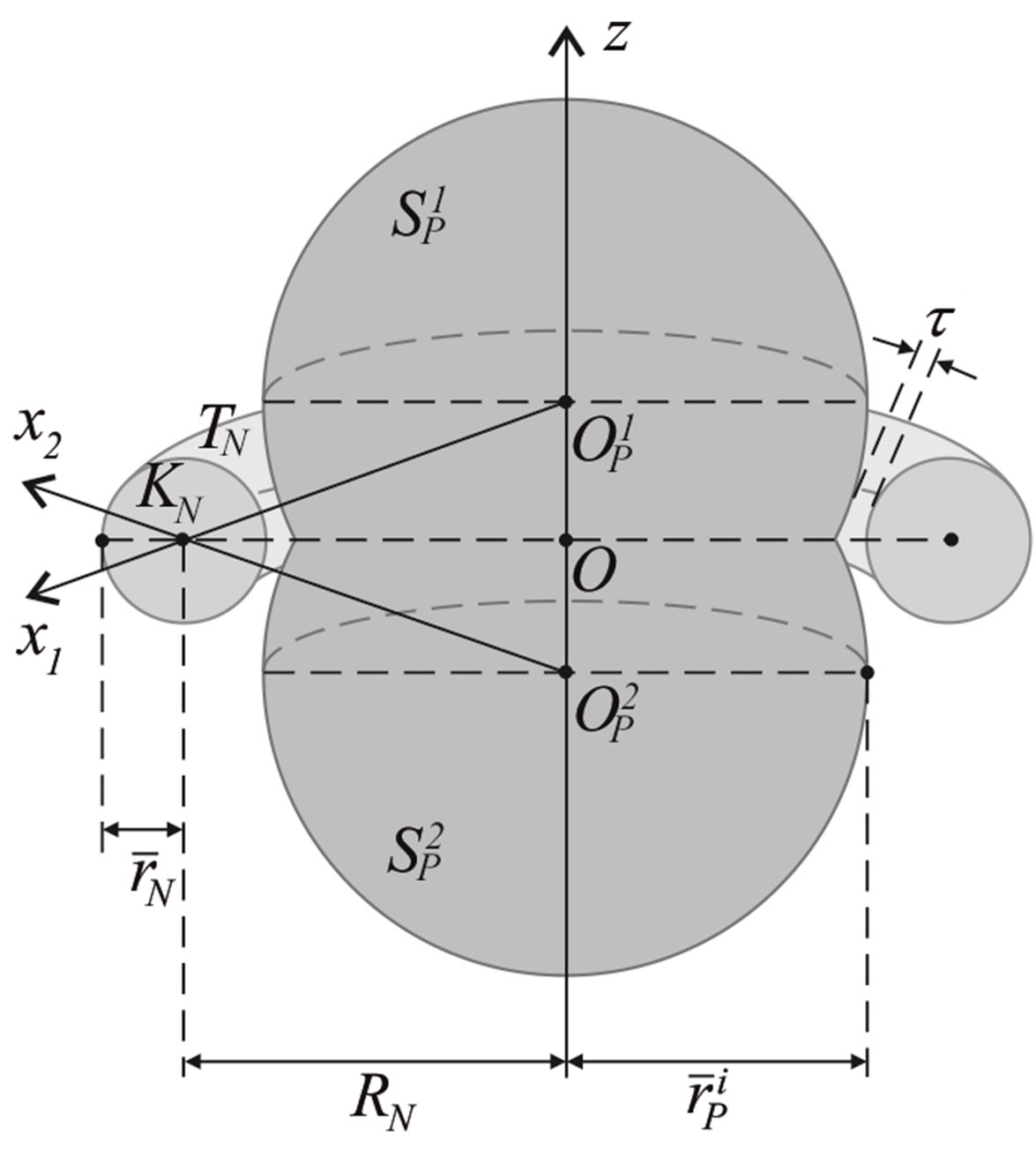
Figure 5. Cross section of the reduced model of the triton.
 J. Using the corresponding Eq.
J. Using the corresponding Eq.
11, we confirm this value for
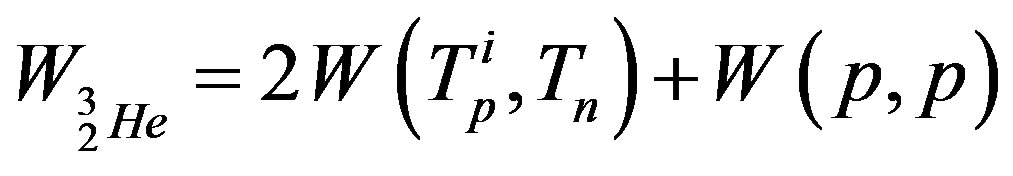 , where
, where 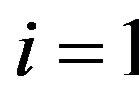 or
or . By virtue of the same Eq.11 we find the magnitude of the interaction force for the helion
. By virtue of the same Eq.11 we find the magnitude of the interaction force for the helion
 , where
, where  or
or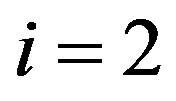 .
.
In Table 2,  and
and  denote the radii of the forming circles, while
denote the radii of the forming circles, while 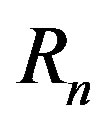 and
and  are the radii of the central circles of the neutron and the proton tori in the helion, respectively. In addition,
are the radii of the central circles of the neutron and the proton tori in the helion, respectively. In addition,  is the interaction force between the nucleons in the helion.
is the interaction force between the nucleons in the helion.
It is important to note that in order to obtain the value of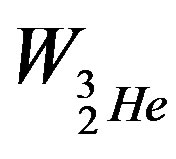 , we can vary
, we can vary  as well for different values of the distance
as well for different values of the distance , such that
, such that  holds. This implies that the distance
holds. This implies that the distance 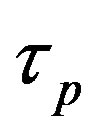 between the surfaces of the two protons will vary according to
between the surfaces of the two protons will vary according to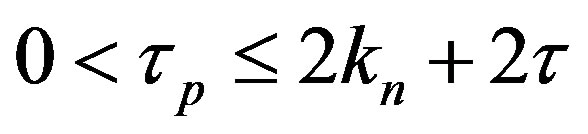 .
.
5. MODEL OF THE ALPHA PARTICLE
Structurally, the alpha particle is obtained by adding one neutron to the helion. We assume that the centres of the protons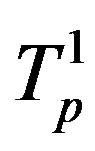 ,
, 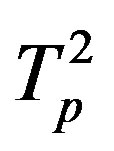 and the neutrons
and the neutrons ,
, 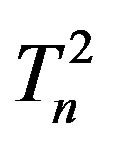 are symmetrically located with respect to the mass centre of the nucleus. The central circles of the tori lie in parallel planes. The distance between the tori
are symmetrically located with respect to the mass centre of the nucleus. The central circles of the tori lie in parallel planes. The distance between the tori ,
,  (
( ) is the same
) is the same  m, while the elongation between
m, while the elongation between ,
, 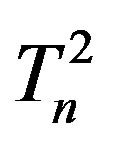 is some small distance (Figure 6).
is some small distance (Figure 6).
From this configuration it follows the stability of the alpha particle is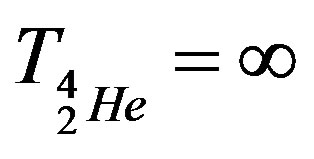 .
.
The centres  and
and 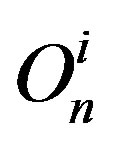 (
( ) of the tori
) of the tori  and
and  lie on one axis
lie on one axis 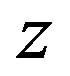 perpendicular to the plane of rotation. The tori
perpendicular to the plane of rotation. The tori  and
and  rotate in the same direction around
rotate in the same direction around  with constant angular velocity
with constant angular velocity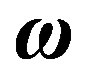 , while
, while  and
and  rotate with the same velocity in the opposite direction. It follows that both the spin and the magnetic moment of the alpha particle are zero, which is an experimentally established fact [15,16].
rotate with the same velocity in the opposite direction. It follows that both the spin and the magnetic moment of the alpha particle are zero, which is an experimentally established fact [15,16].
Moreover, the decrease of the centrifugal force as compared to the helion implies that the radius of the

Figure 6. Cross section of the model of the alpha particle.
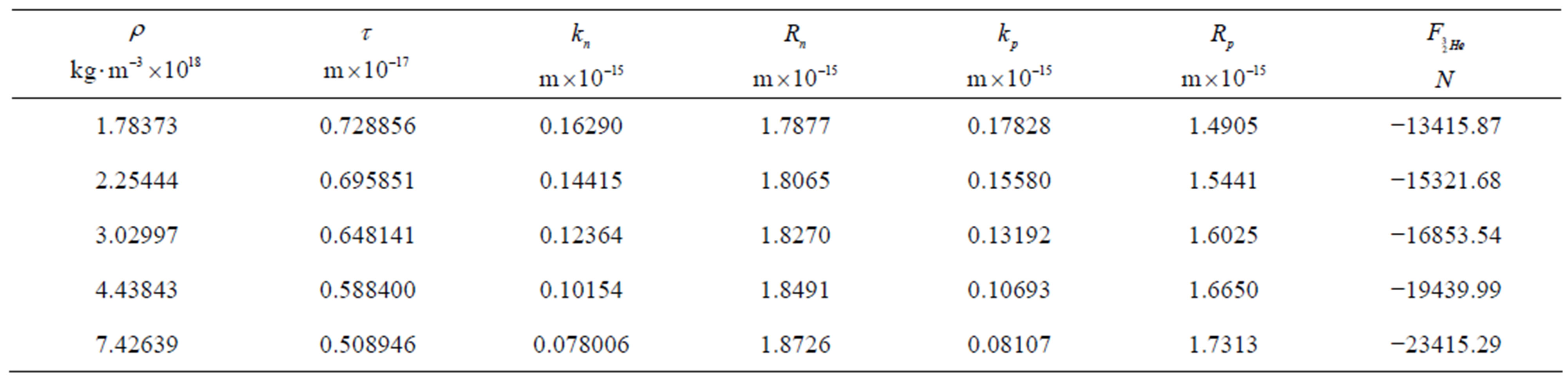
Table 2. Dimensions of nucleons and interaction force between them in the helion.
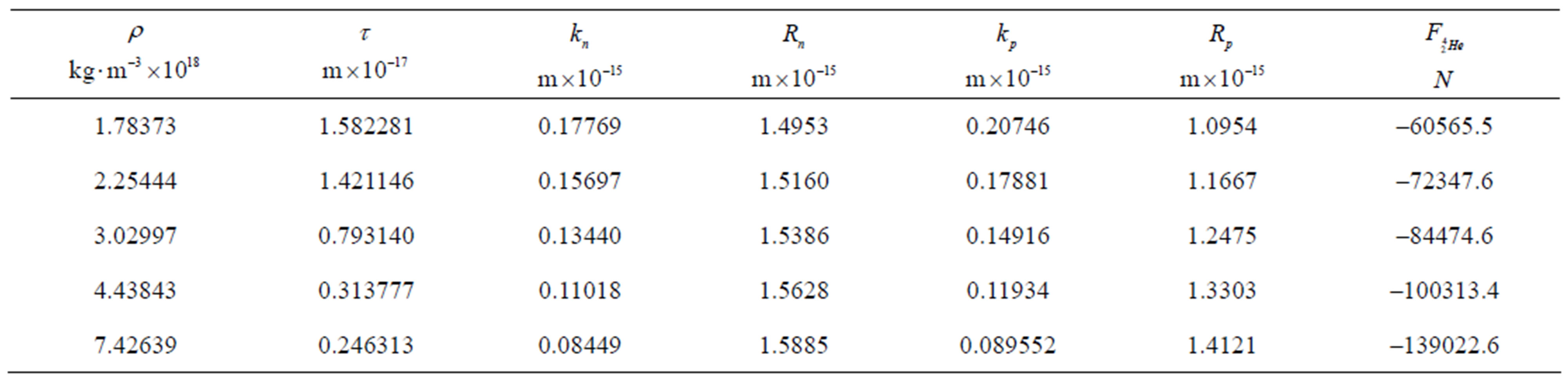
Table 3. Dimensions of nucleons and the interaction force in the alpha particle.
alpha particle 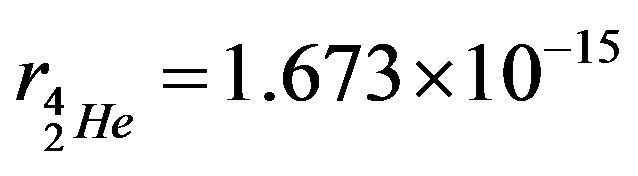 m [17] is smaller than the radius of the helion
m [17] is smaller than the radius of the helion  m.
m.
Let  and
and 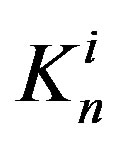 be the centres of the forming circles of
be the centres of the forming circles of  and
and 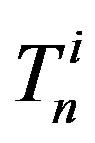 with radii
with radii 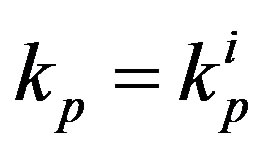 and
and 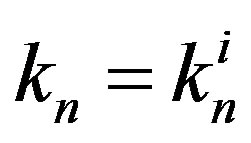
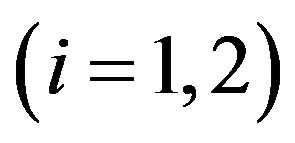 . For
. For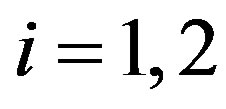 , we denote
, we denote  and
and 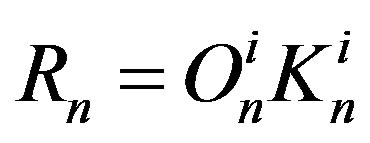 (Figure 6).
(Figure 6).
The radius of the neutron is equal to the radius of the alpha particle, that is  and
and . From the isosceles trapezoid
. From the isosceles trapezoid 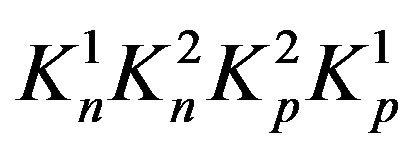 it follows that the distance
it follows that the distance 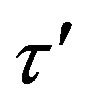 between the surfaces of the tori
between the surfaces of the tori 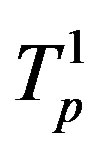 and
and 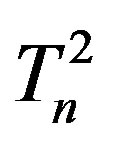 is
is
 . (13)
. (13)
We assume again that the proton charges are concentrated in their geometric centres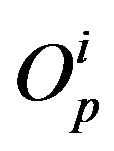 . Similar to Section 4, we model the protons as spheres
. Similar to Section 4, we model the protons as spheres  with centres
with centres 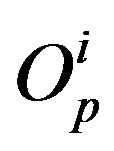 and radii
and radii 
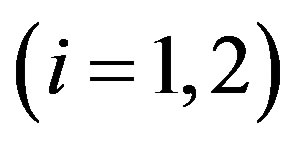 , whose areas are equal to that of
, whose areas are equal to that of . Moreover, the charge of
. Moreover, the charge of 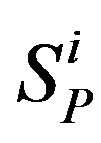 is
is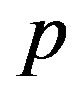 , which is spherically symmetric and can be redistributed.
, which is spherically symmetric and can be redistributed.
With 
 , we denote the tori, whose areas are equal to the areas of
, we denote the tori, whose areas are equal to the areas of  with the same centres
with the same centres . The distance between the objects
. The distance between the objects 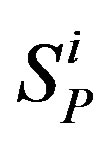 and
and 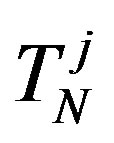 is the same as the distance between
is the same as the distance between 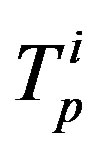 and
and 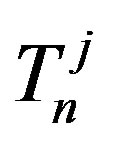
 . Let us denote: with
. Let us denote: with  the sphere whose central circle is the forming circle of the torus
the sphere whose central circle is the forming circle of the torus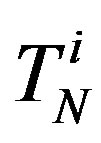 ; with
; with 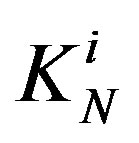 the center of the sphere and with
the center of the sphere and with  the radius of the sphere (Figure 6).
the radius of the sphere (Figure 6).
We further assume that the points  and
and 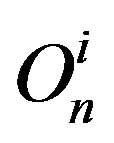
 are at rest with respect to an inertial reference frame
are at rest with respect to an inertial reference frame . In addition, four firm noninertial coordinate systems
. In addition, four firm noninertial coordinate systems 
 are introduced rotating at constant angular velocity
are introduced rotating at constant angular velocity  (or
(or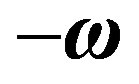 ) equal to the angular velocity of rotation of the neutrons
) equal to the angular velocity of rotation of the neutrons 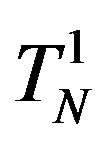 and
and 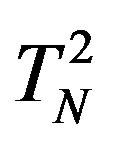 with respect to
with respect to . Every point
. Every point 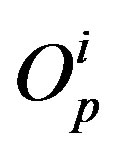 is a centre of two coordinate systems
is a centre of two coordinate systems 
 fixed firmly with the reference frames
fixed firmly with the reference frames  with respect to which the spheres
with respect to which the spheres  and
and  are at rest.
are at rest.
Since the total charges of the tori  and
and  are zero it can be assumed with good approximation that there is no electrostatic interaction between them.
are zero it can be assumed with good approximation that there is no electrostatic interaction between them.
Due to the symmetry, it suffices to find the interaction between any of the spheres  and the spheres
and the spheres 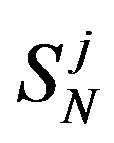
 . We assume as we noted in Section 4 that the interaction between the spheres
. We assume as we noted in Section 4 that the interaction between the spheres 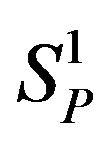 and
and 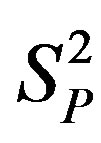 is taken as point charges
is taken as point charges , i.e.
, i.e. 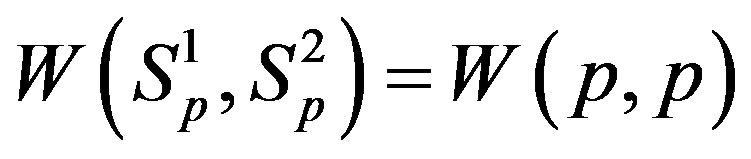 and
and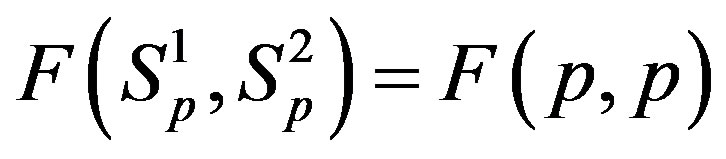 . For the sake of calculative simplicity it is assumed that the distance
. For the sake of calculative simplicity it is assumed that the distance  between the surfaces of the proton tori
between the surfaces of the proton tori  and
and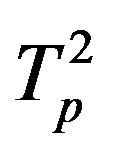 , as well as the distance
, as well as the distance 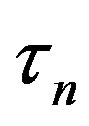 between the surfaces of the neutron tori
between the surfaces of the neutron tori  and
and , is the same as the one between
, is the same as the one between  and
and 
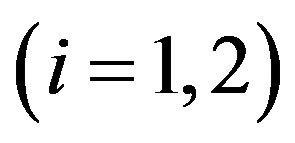 , i.e.
, i.e.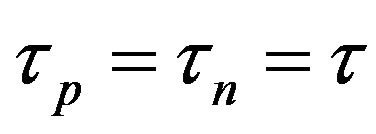 .
.
We have  and
and . Therefore,
. Therefore,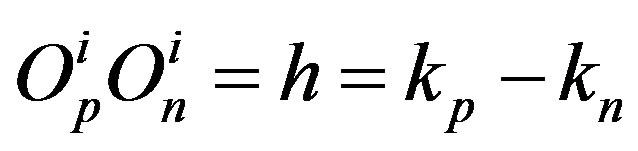 . Taking into account the mass density
. Taking into account the mass density 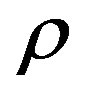 of the nucleons from Table 1 of Section 3 and using Eqs.1-5 from Section 2 for different values
of the nucleons from Table 1 of Section 3 and using Eqs.1-5 from Section 2 for different values  all parameters
all parameters ,
,  and
and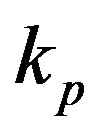 ,
,  ,
, 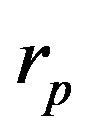 can be found. In Eqs.3 and 4 the corresponding mass defect for the two protons and the two neutrons has been taken into account. According to Eqs.7-9 we calculate
can be found. In Eqs.3 and 4 the corresponding mass defect for the two protons and the two neutrons has been taken into account. According to Eqs.7-9 we calculate ,
, 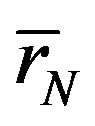 and the distances
and the distances 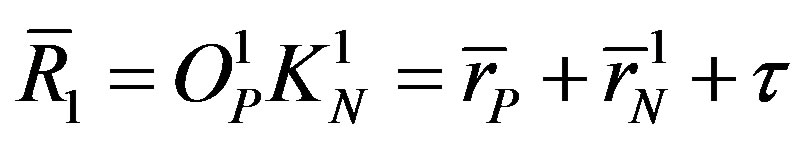 and
and  between the centres of the spheres
between the centres of the spheres 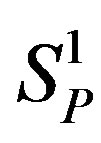 ,
,  and
and ,
, 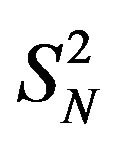 , where
, where 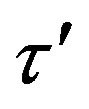 is given by Eq.13.
is given by Eq.13.
The experimentally established mass of the alpha particle is  kg [15]. According to Eq.12 the binding energy for the alpha particle
kg [15]. According to Eq.12 the binding energy for the alpha particle  J. Using the corresponding Eq. 11 we confirm this value for
J. Using the corresponding Eq. 11 we confirm this value for 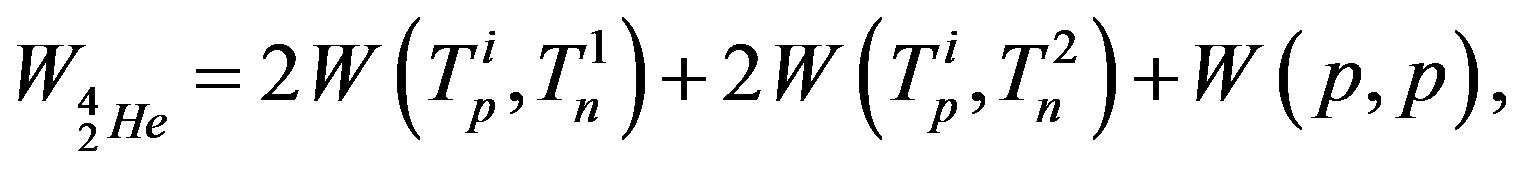 where
where
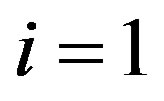 or
or . By virtue of the same Eq.11 we find the magnitude of the interaction force for the alpha particle
. By virtue of the same Eq.11 we find the magnitude of the interaction force for the alpha particle
 , where
, where 
or .
.
The quantities  and
and  in Table 3 denote the radii of the forming circles of the tori,
in Table 3 denote the radii of the forming circles of the tori,  and
and 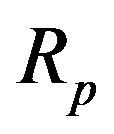 are the radii of the central circles of the neutron and proton tori, respectively and
are the radii of the central circles of the neutron and proton tori, respectively and  is the interaction force between the nucleons in the alpha particle.
is the interaction force between the nucleons in the alpha particle.
We would like to note that in order to obtain the value of , the quantity
, the quantity  for different values of the distance
for different values of the distance  can be varied as well, such that
can be varied as well, such that 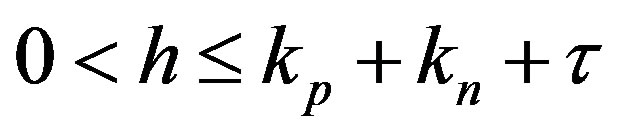 . It follows that the distance
. It follows that the distance  between the proton surfaces will vary
between the proton surfaces will vary . According to Eq.13 the distance
. According to Eq.13 the distance  will vary, too.
will vary, too.
6. DISCUSSION
Describing the nucleons as tori, we calculate in [8] the potential energy and the interaction force between the nucleon couples. This approach is based on recently derived for the first time analytical expressions describing the electrostatic interaction between two charged spheres in the most general case [10]. According to the above mentioned formulae one can determine the electrostatic interaction between spheres at distances much less than their radii.
Based on this method, we find that strong interactions in atomic nuclei are electromagnetic in origin. Additional finding is the fact that the electrostatic interactions between the couples proton-neutron are short range (attracting forces), while the interactions between the couples proton-proton are long range ones (repelling forces) [18].
In [9] the basic experimental results for the deuteron and the triton such as binding energy, radii, spins and magnetic moments have been explained.
In the present paper, we extend this investigation for the nuclei of helium-3 and helium-4 and confirm that our model is capable to explain all essential experimental results for the basic simple nuclei. We find new results— the volumes and the mass densities of the nuclei, as well as the force of interaction in the considered nuclei.
7. CONCLUSIONS
The presented here model can be applied for the more complicated atomic nuclei. The electrostatic interaction between nucleons changes their electric structure. Thus, all nucleons enter to various extents in interactions, which compensate each other.
Let us also note that the electromagnetic forces between nucleons depend on whether they rotate in the same or different directions that is they depend on the orientation of their spins.
Based on our research, we are confident that all available experimental data about atomic nuclei can be explained by the model proposed. Other new properties of atomic nuclei can also be found.
It is essential that we obtain the basic nuclear characteristic—the binding energy in all of the considered nuclei, using only electromagnetic interactions. The most significant conclusion from our studies is that nuclear forces are electromagnetic in origin.
8. ACKNOWLEDGEMENTS
The author would like to thank Stefan Bozhkov, for performing the calculations in the present paper on Wolfram Mathematica 7.0.
The results of the present studies are published with the financial support from the Fund for Scientific Research at the Ministry of Education and Science of Bulgaria under contract DTC No. 02/35.
REFERENCES
- Standard model. http://en.wikipedia.org/wiki/Standard_Model.
- University of Tennessee. Standard model. http://electron6.phys.utk.edu/phys250/modules/module%206/standard_model.htm
- Fehling, D. The standard model of particle physics: A lunchbox’s guide. http://www.pha.jhu.edu/~dfehling/
- Bergman, D. (2000) The real proton. Foundations of Science, 3, 4.
- Toroidal ring model. http://www.enotes.com/topic/Toroidal_ring_model
- Toroidal ring model. http://en.wikipedia.org/wiki/Toroidal_ring_model
- Twain, M. (1995) The undiscovered physics. http://groupkos.com/mtwain/TheProton.pdf.
- Kolikov, K., Ivanov, D. and Krustev, G. (2012) Electromagnetic nature of the nuclear forces and a toroid model of nucleons in atomic nuclei. Natural Science, 4, 47-56. doi:10.4236/ns.2012.41008
- Kolikov, K., Ivanov, D. and Krustev, G. (2012) Electromagnetic nature of the nuclear forces and toroid structure of the deuteron and triton. Natural Science, 4, 123-130. doi:10.4236/ns.2012.42018
- Kolikov, K., Ivanov, D., Krustev, G., Epitropov, Y. and Bozhkov, S. (2011) Electrostatic interaction between two conducting spheres. Journal of Electrostatics, 70, 91-96. doi:10.1016/j.elstat.2011.10.008.
- Feynman, R. (1964) The Feynman lectures on physics: Exercises. Addison Wesley Publishing Co., Boston.
- Gellert, W., Kästner, H. and Neuber, S. (1983) Mathematical encyclopedic dictionary, science and art, Sofia. 585 (in Bulgarian).
- Sardin, G. (1999) Fundamentals of the orbital conception of elementary particles and of their application to the neutron and nuclear structure. Physics Essays, 12, 204- 220. doi:10.4006/1.3025378
- Sick, I. (2003) On the rms-radius of the proton. Physics Letters B, 576, 62-67. doi:10.1016/j.physletb.2003.09.092
- Mohr, P., Taylor, B. and Newell, D. (2008) CODATA recommended values of the fundamental physical constants: 2006. http://arxiv.org/abs/0801.0028
- Krane, K. (1999) Introductory nuclear physics. WileyVCH, Weinheim.
- Wang, L.B., Mueller, P., Bailey K., Drake G.W., Greene J.P., et al. (2004) Laser spectroscopic determination of 6He nuclear charge radius. Physical Review Letters, 93, 142501. doi:10.1103/PhysRevLett.93.142501
- Ivanov, D. and Kolikov, K. (Unpublished) Short-range action and long-range action of the electrostatic forces within atomic nuclei.

