Natural Science
Vol.4 No.5(2012), Article ID:19121,9 pages DOI:10.4236/ns.2012.45047
On consistency and ranking of alternatives in uncertain AHP*
![]()
College of Science, Guilin University of Technology, Guilin, China; #Corresponding Author: linliang6666@126.com
Received 10 March 2012; revised 15 April 2012; accepted 21 April 2012
Keywords: Uncertainty Theory; Uncertain Variable Method; Analytic Hierarchy Process; Consistency Test; Bounds Modification
ABSTRACT
This paper introduces uncertainty theory to deal with non-deterministic factors in ranking alternatives. The uncertain variable method (UVM) and the definition of consistency for uncertainty comparison matrices are proposed. A simple yet pragmatic approach for testing whether or not an uncertainty comparison matrix is consistent is put forward. In cases where an uncertainty comparison matrix is inconsistent, an algorithm is used to generate consistent matrix. And then the consistent uncertainty comparison matrix can derive the uncertainty weights. The final ranking is given by uncertainty weighs if they are acceptable; otherwise we rely on the ranks of expected values of uncertainty weights instead. Three numerical examples including a hierarchical (AHP) decision problem are examined to illustrate the validity and practicality of the proposed methods.
1. INTRODUCTION
The Analysis Hierarchy Process (AHP) is a multicriteria decision making (MCDM) technique introduced by Saaty [1], that generates the relative weights of criteria. The advantages of this MCDM tool are its conceptual simplicity and its capability of handling subjective criteria and inconsistencies in the decision making process. As such the estimation of the relative weights of attributes plays a critical role in MCDM. Saaty [1] proposed to use single points as the elements of the comparison matrices. Each element reflects the degree of preference of one attributes over another and is taken from the 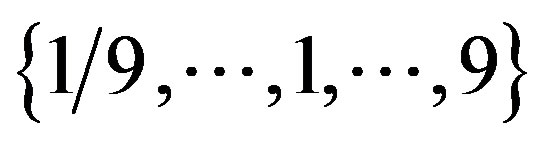 ratio scale. However, due to the complexity and uncertainty involved in real-world decision problems and inherent subjective nature of human preference judgments, it is always unrealistic and infeasible to obtain exact judgments. Then the methods using fuzzy or interval judgments for parts or all of the judgments in a pairwise comparison matrix are proposed naturally. A number of techniques have been developed to use such a fuzzy or interval comparison matrix to derive weights. In the following section, we summarize the previous works and propose our new approach of uncertain variable method.
ratio scale. However, due to the complexity and uncertainty involved in real-world decision problems and inherent subjective nature of human preference judgments, it is always unrealistic and infeasible to obtain exact judgments. Then the methods using fuzzy or interval judgments for parts or all of the judgments in a pairwise comparison matrix are proposed naturally. A number of techniques have been developed to use such a fuzzy or interval comparison matrix to derive weights. In the following section, we summarize the previous works and propose our new approach of uncertain variable method.
Van Laarhoven and Pedryce [2] considered treating entries in a comparison matrix as fuzzy numbers having triangular membership functions and proposed the logarithmic least squares method to generate fuzzy weights. Buckley [3] extended the method to trapezoidal membership functions. Modifying Van Laarhoven and Pedrycz’s method (1983), Boender et al. [4] pointed out a fallacy in the normalization procedure for generating fuzzy weights. Kwiesielewicz [5] found the extension of Saaty’s priority theory. Leung and Cao [6] proposed a fuzzy consistency definition with consideration of a tolerance deviation and determined fuzzy local and global weights using the extension principle. Xu and Da [7] introduced a least deviation method to obtain a priority vector of a fuzzy preference relation. However, most of the above fuzzy priority techniques take little account of inconsistent judgments.
Saaty and Vargas [8] employed interval judgments for the AHP method as a way to model subjective uncertainty and applied a Monte Carlo simulation approach to find out weight intervals from matrices of interval judgments. At the same time, they also pointed out difficulties in using this method. Arbel [9] proposed linear programming (LP) model as the prioritization process. Kress [10] pointed out that Arbel’s method is inefficient for inconsistent interval comparison matrices because no feasible region exists in such situations. Islam [11] used lexicographic goal programming (LGP) to find out weights from pairwise inconsistent interval judgment matrices and an algorithm for identification and modification of inconsistent bounds was also provided. Linda M. Haines
[12] employed a statistical approach to the AHP with interval judgments and constructed the distributions on feasible regions. Wang, Yang and Xu [13] proposed a two-stage logarithmic goal programming method (TLGP) for generating weights from interval comparison matrices and it was also applied to fuzzy comparison matrices when they were transformed into interval comparison matrices using 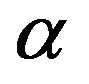 -level sets and the extension principle. Uncertainty in the preference judgments gave rise to uncertainty in the ranking of alternatives as well as difficulty in determining consistency of preferences.
-level sets and the extension principle. Uncertainty in the preference judgments gave rise to uncertainty in the ranking of alternatives as well as difficulty in determining consistency of preferences.
As is well known, we must test the consistency of comparison matrices in the process of generation weights. Because of the complexity and uncertainty of real-world decision analysis problems and the subjectivity of human judgments, it is inevitable to generate inconsistent comparisons. Unreliable weights and ranking orders for alternatives may be caused by high inconsistency. Then it is necessary to check satisfactory consistency in order to ensure the rationality of decisions. Only comparison matrices passing the test of satisfactory consistency can be used to derive reliable weights. In this case, Saaty proposed the use of Consistency Ratio (CR). This consistency measure is obtained by taking the ratio between 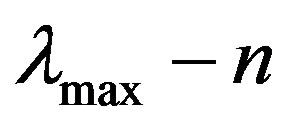 to its expected value over a large number of positive reciprocal matrices of order
to its expected value over a large number of positive reciprocal matrices of order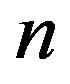 , whose elements are randomly chosen in the
, whose elements are randomly chosen in the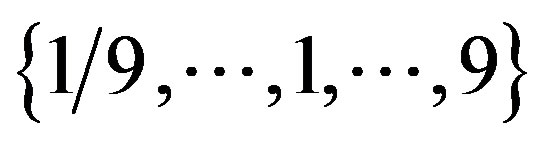 . Juan Aguarón and José María Moreno-Jiménez [14] employed Geometric Consistency Index (GCI) which can be seen as an average of the squared difference between the log of the errors and the log of unity. Leung and Cao [6] introduced the definition of fuzzy consistency and Wang et al. [15] proposed the consistency of interval comparison matrix both using the concept of feasible region
. Juan Aguarón and José María Moreno-Jiménez [14] employed Geometric Consistency Index (GCI) which can be seen as an average of the squared difference between the log of the errors and the log of unity. Leung and Cao [6] introduced the definition of fuzzy consistency and Wang et al. [15] proposed the consistency of interval comparison matrix both using the concept of feasible region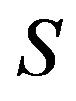 . Although we can test the consistency of matrices, how to modify the inconsistent matrices in order to derive the weights of attributes is still not solved. An algorithm provided by Islam et al. [11] for identification and modification of inconsistent bounds is used in our paper. With this algorithm the inconsistent matrices can be transformed into consistent ones without any more information. Due to the drawbacks of weights generation approaches mentioned above here we propose a new approach called uncertain variable method to derive weights from both consistent and inconsistent uncertainty comparison matrices.
. Although we can test the consistency of matrices, how to modify the inconsistent matrices in order to derive the weights of attributes is still not solved. An algorithm provided by Islam et al. [11] for identification and modification of inconsistent bounds is used in our paper. With this algorithm the inconsistent matrices can be transformed into consistent ones without any more information. Due to the drawbacks of weights generation approaches mentioned above here we propose a new approach called uncertain variable method to derive weights from both consistent and inconsistent uncertainty comparison matrices.
Uncertainty theory, proposed by Liu [16] in 2007 and refined by Liu [17] in 2010, provides a new approach to deal with non-deterministic factors. Firstly, uncertain variable (Liu [16]) instead of precise ratio is used to represent human judgments. Then uncertain measure (Liu [16]) is used to indicate the belief degree of an uncertain event. Subsequently uncertainty distribution (Liu [16]) is used to describe uncertain variables in an incomplete but
easy-to-use way. Based on uncertainty comparison matrix, priorities are derived by using inverse uncertainty distribution (Liu [18]) without any optimization model and ranking with a certain confidence level is obtained. Finally, consistency of matrices is tested and the inconsistent matrices are modified. At the end, the reliable weights can be obtained. The decision problem model is called uncertain AHP [19] when uncertain variable is brought in. This paper is focused only on the generating uncertainty weights, ranks of alternatives and modification of inconsistent matrices.
This paper is organized as follows. Section 2 proposes the uncertain variable method (UVM) to generate uncertainty weights from both consistent and inconsistent uncertainty comparison matrices. In Section 3, the definition of consistency for uncertainty comparison and the theorem for checking consistency are expressed, and then we develop a simple yet pragmatic approach that can be used to test whether an uncertainty comparison matrix is consistent or not without solving any mathematical program. Moreover an algorithm for identification and modification of inconsistent bounds is discussed. Section 4 provides three numerical examples including a hierarchical (AHP) decision problem to show the simplicity and practicality of the proposed methods. The paper is concluded in Section 5.
2. AN UNCERTAIN VARIABLE METHOD (UVM) FOR GENERATING UNCERTAINTY WEIGHTS
As we all know, fuzzy ratios and interval ratios were used to describe uncertainty of human judgments in previous works. Here in our paper, we introduce uncertain variable (Liu [16]) with uncertainty distribution to reflect the uncertain nature of expert judgments.
Let 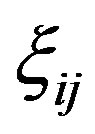 be an uncertain variable represents the ratio criterion
be an uncertain variable represents the ratio criterion 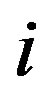 over criterion j. We assume that its uncertainty distribution (Liu [16]) is linear uncertainty distribution and can be obtained by Delphi method. The consultation process is as follows:
over criterion j. We assume that its uncertainty distribution (Liu [16]) is linear uncertainty distribution and can be obtained by Delphi method. The consultation process is as follows:
Q1: What do you think is the minimum ratio criterion 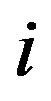 over criterion
over criterion ?
?
A1: a. (an expert’s experimental data 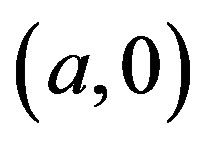 is acquired)
is acquired)
Q2: What do you think is the maximum ratio criterion  over criterion j?
over criterion j?
A2: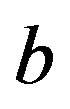 . (an expert’s experimental data
. (an expert’s experimental data 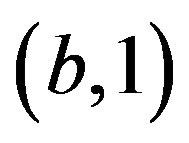 is acquired)
is acquired)
where (a,0), (b,1) represents 
 , respectively. So the uncertainty ratio
, respectively. So the uncertainty ratio  has an uncertainty distribution
has an uncertainty distribution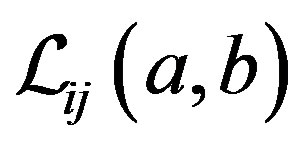 . Repeating the steps, we can get a matrix given by
. Repeating the steps, we can get a matrix given by
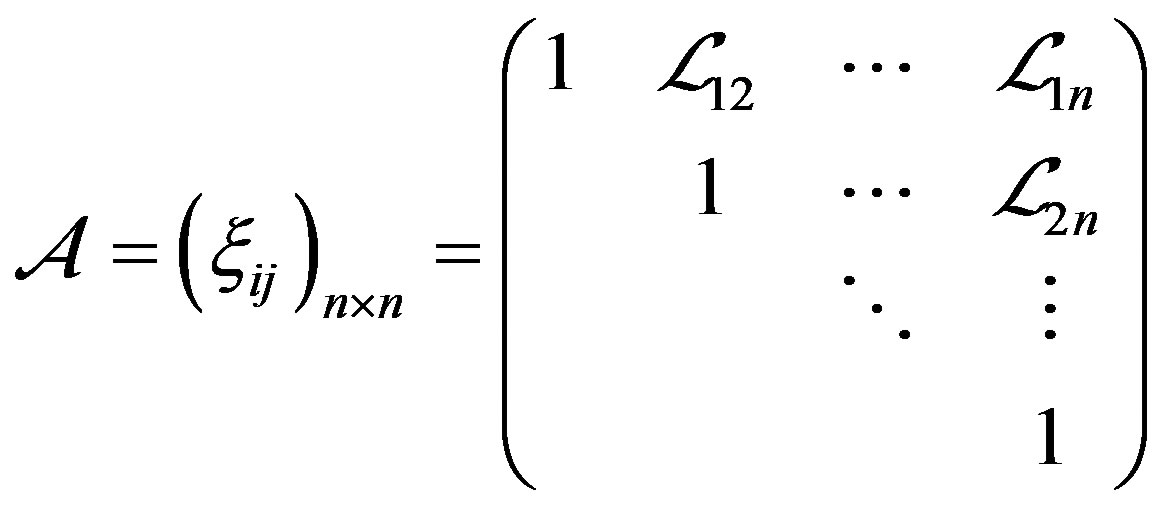 (1)
(1)
Since uncertainty distributions 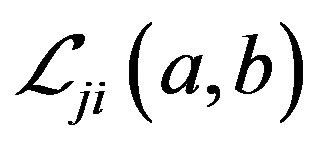
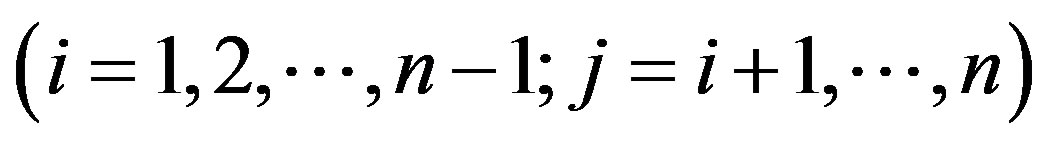 of inverse uncertainty ratios
of inverse uncertainty ratios  cannot be easily determined in the sense of definition of uncertain measure (Liu [16]). So, in this paper, we just need to obtain the uncertainty distributions of upper triangular uncertainty ratios, the lower triangular uncertainty ratios can be obtained by inverse uncertainty distribution (Liu [16]) below
cannot be easily determined in the sense of definition of uncertain measure (Liu [16]). So, in this paper, we just need to obtain the uncertainty distributions of upper triangular uncertainty ratios, the lower triangular uncertainty ratios can be obtained by inverse uncertainty distribution (Liu [16]) below
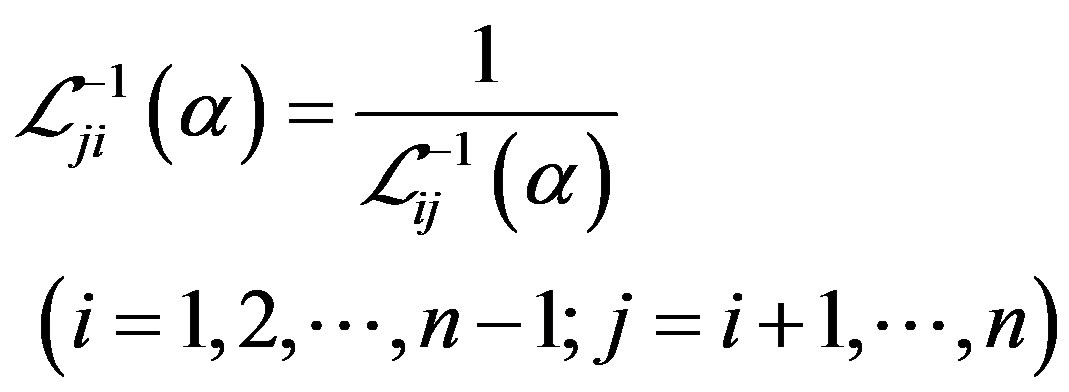 (2)
(2)
where  is the uncertain measure with
is the uncertain measure with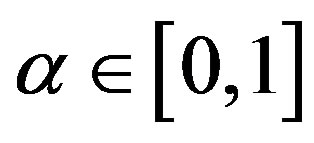 .
.  is called uncertainty comparison matrix.
is called uncertainty comparison matrix.
Crawford and Williams [20] suggested for the Row Geometric Mean Method (RGMM), where the priorities (without the normalization factor) are given by
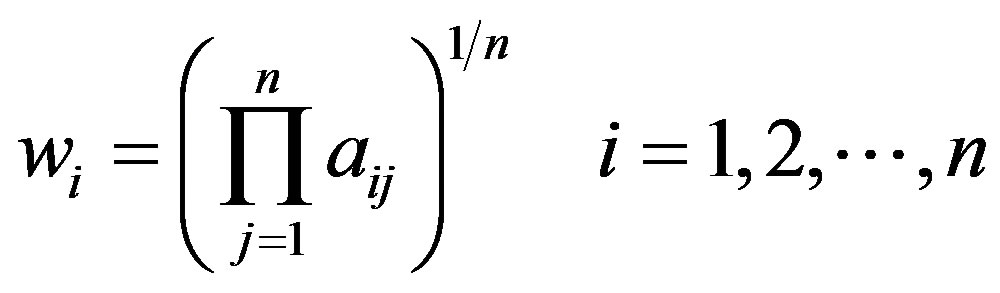 (3)
(3)
where wi is the weight of the 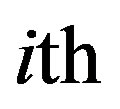 attribute. Liu [16] proposed the concept of strictly increasing function of uncertain variables. A real-valued function
attribute. Liu [16] proposed the concept of strictly increasing function of uncertain variables. A real-valued function 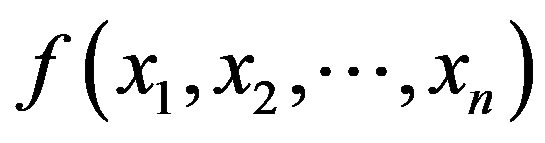 is said to be strictly increasing if
is said to be strictly increasing if
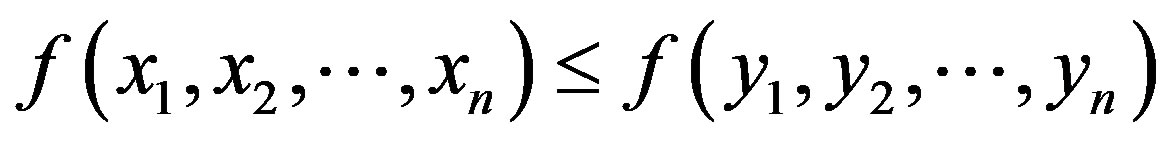
whenever  for
for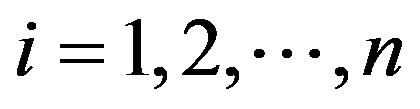 , and
, and
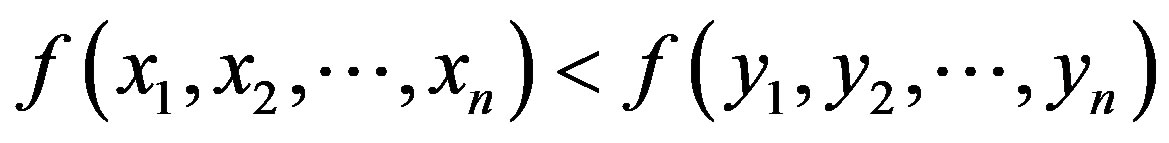
whenever 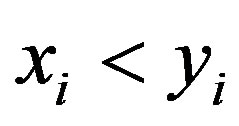 for
for 
Eq.2 can be expressed as
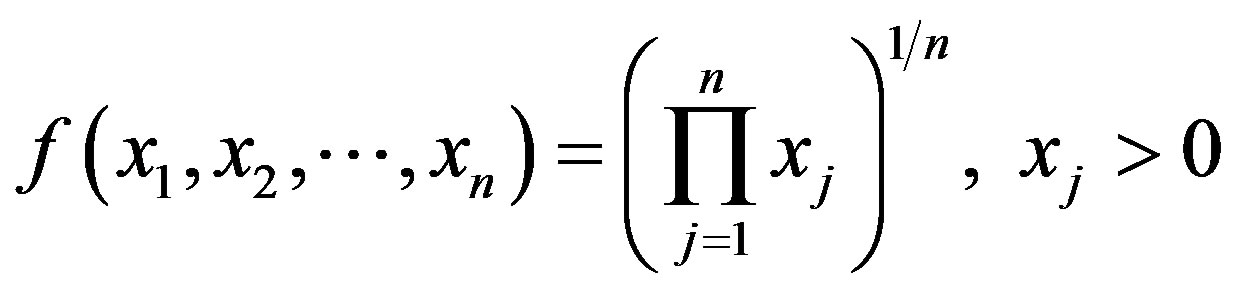
then f is a strictly increasing function.
Theorem 2.1 (Liu [17]) Let 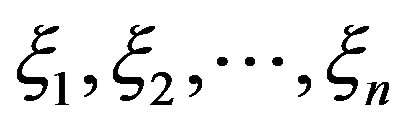 be independent uncertain variables with regular uncertainty distribution
be independent uncertain variables with regular uncertainty distribution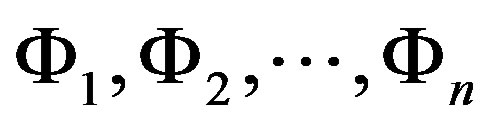 , respectively. If
, respectively. If 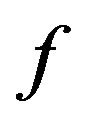 is a strictly increasing function, then
is a strictly increasing function, then
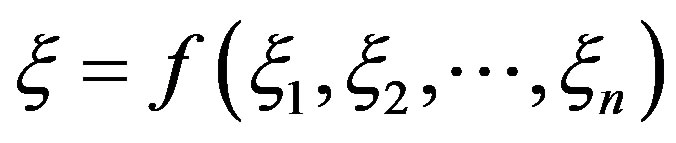
is an uncertain variable with inverse uncertainty distribution
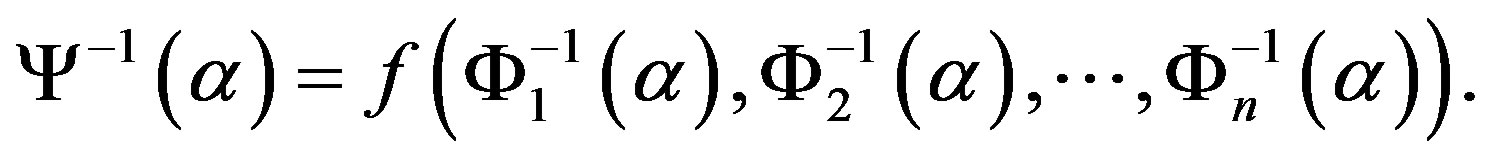
By the Theorem 2.1, we know that 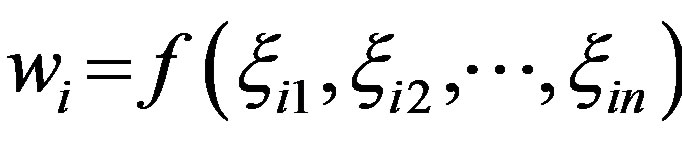 is an uncertain variable with inverse uncertainty distribution
is an uncertain variable with inverse uncertainty distribution
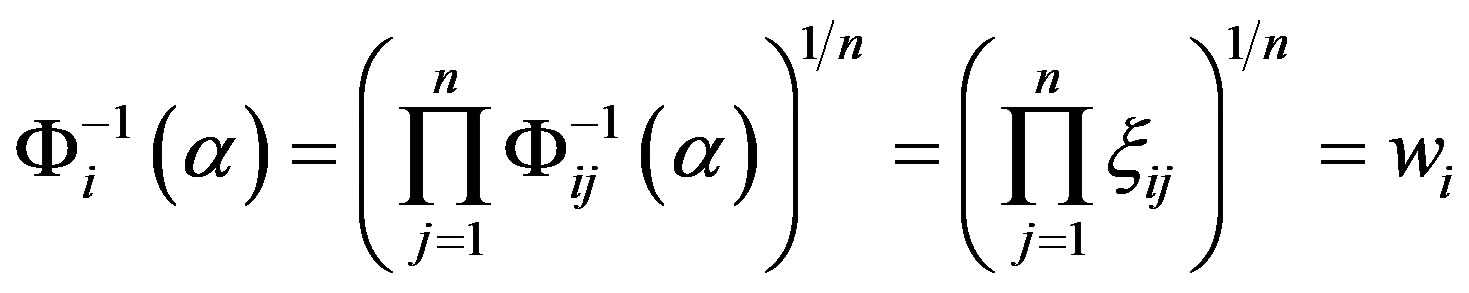 (4)
(4)
where 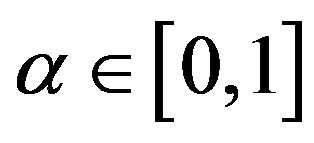 is the uncertain measure.
is the uncertain measure.  is defined as uncertainty weight of the
is defined as uncertainty weight of the 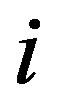 th attribute. We consider the weights acceptable when the ranking order does not alter if
th attribute. We consider the weights acceptable when the ranking order does not alter if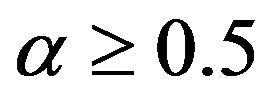 . Otherwise experts will be asked to provide new judgments. Without any modification or new information, we rely on the ranks of expected values of uncertainty weights instead.
. Otherwise experts will be asked to provide new judgments. Without any modification or new information, we rely on the ranks of expected values of uncertainty weights instead.
Note that the weight 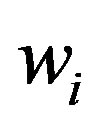 is an uncertain variable and can not be used to test consistency of matrices. So which group of weights can be used to check the consistency will be asked. Liu and Ha [21] give the expected value
is an uncertain variable and can not be used to test consistency of matrices. So which group of weights can be used to check the consistency will be asked. Liu and Ha [21] give the expected value 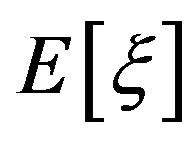 of monotone function of uncertain variables
of monotone function of uncertain variables
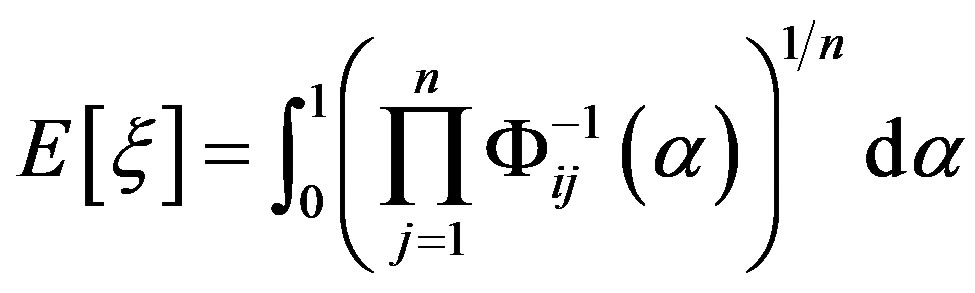 (5)
(5)
which is a precise number representing expected value of uncertain variable  (priority of
(priority of  attribute) in Eq.4. However the integral can not be found, only the numerical solution of the expected value could be calculated by computer.
attribute) in Eq.4. However the integral can not be found, only the numerical solution of the expected value could be calculated by computer.
3. IDENTIFICATION AND MODIFICATION OF INCONSISTENT BOUNDS
Suppose decision maker (DM) provides uncertainty judgments instead of precise judgments for a pairwise comparison. It can be denoted by Eq.1. About the above uncertainty comparison matrix, we give the following definition and theorem:
Definition 3.1 Let  is an uncertainty comparison matrix defined by (1) with
is an uncertainty comparison matrix defined by (1) with 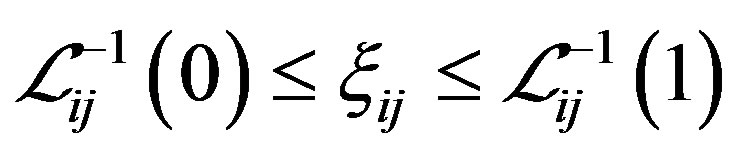 and
and 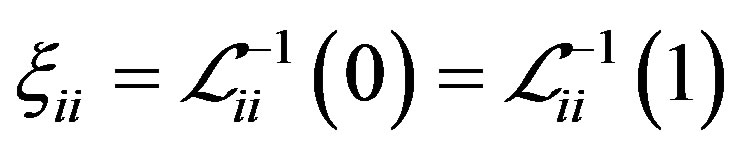 for
for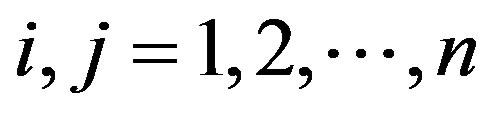 . If the convex feasible region
. If the convex feasible region

is nonempty, then  is considered to be a consistent uncertainty comparison matrix.
is considered to be a consistent uncertainty comparison matrix.
Theorem 3.1  is a consistent uncertainty comparison matrix if and only if it satisfies the following inequality constraints:
is a consistent uncertainty comparison matrix if and only if it satisfies the following inequality constraints:
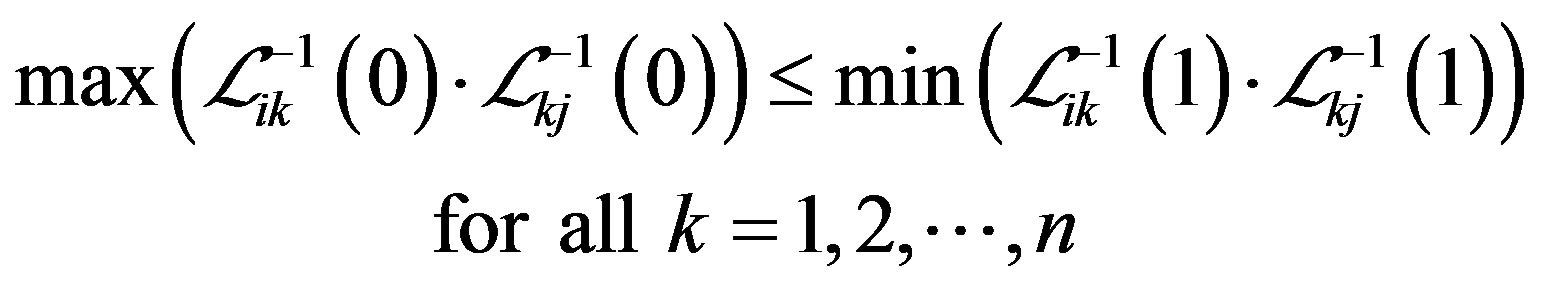 (6)
(6)
Proof. If  is a consistent uncertainty comparison matrix, it means the convex feasible region
is a consistent uncertainty comparison matrix, it means the convex feasible region 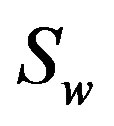 is nonempty and there is no contradiction among the following inequality constraints:
is nonempty and there is no contradiction among the following inequality constraints:
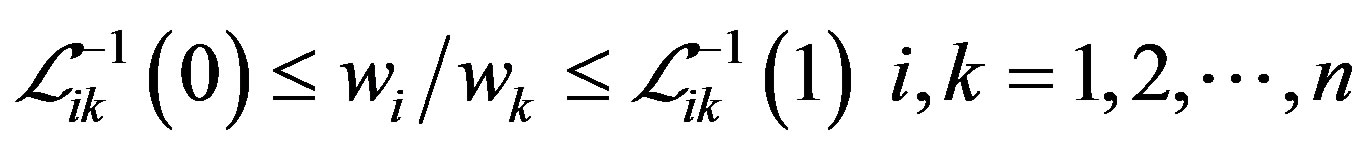 (7)
(7)
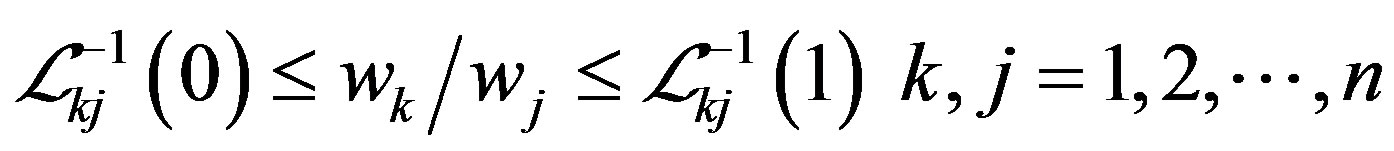 (8)
(8)
Multiplying (7) by (8) leads to the following inequalities
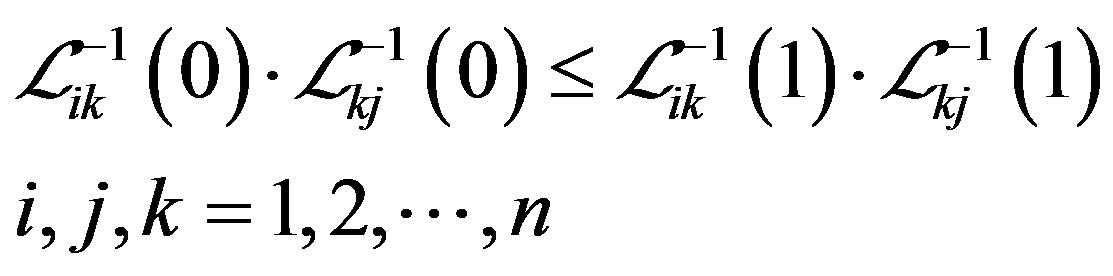 (9)
(9)
Since (9) holds for any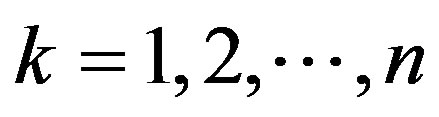 , it follows that
, it follows that
 holds for all
holds for all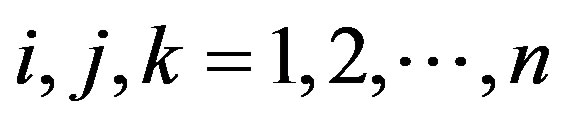 .
.
Inversely, if (6) holds for all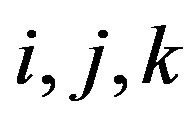 , then
, then 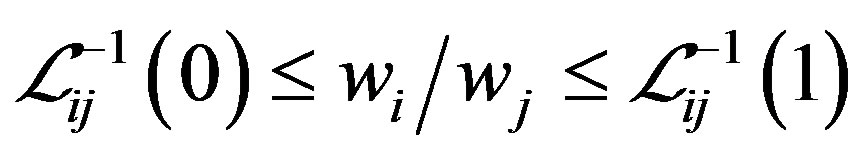 holds for any
holds for any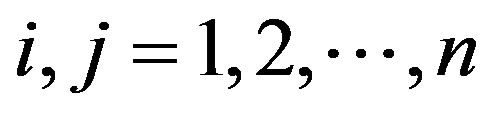 . So,
. So, 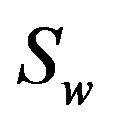 is nonempty and
is nonempty and  is a consistent uncertainty comparison matrix in the sense of Definition 3.1.
is a consistent uncertainty comparison matrix in the sense of Definition 3.1.
We can check the matrices whether they are consistent or not by the Definition 3.1, however it computes inefficiently when the order of matrix is large. So an algorithm proposed by Islam et al. [11],
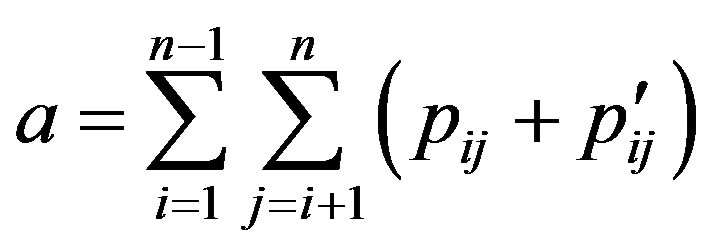 (10)
(10)
subject to

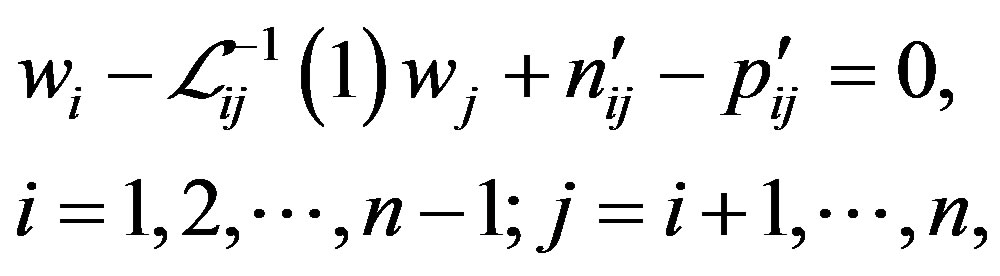
where 
After calculating the weights 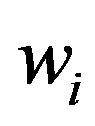 by UVM from uncertainty comparison matrix, the ratios
by UVM from uncertainty comparison matrix, the ratios 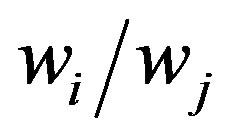 for all
for all 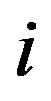 and
and  may or may not belong to the interval
may or may not belong to the interval
 . The
. The 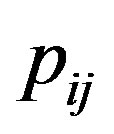 or
or 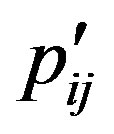 reflects the deviation
reflects the deviation 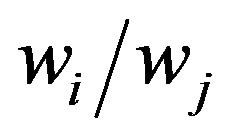 exceeding the set
exceeding the set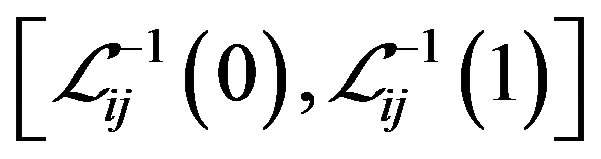 . It is clear that the matrix is consistent if and only if
. It is clear that the matrix is consistent if and only if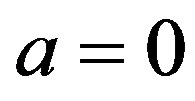 . With the bounds of the set being modified, the value of
. With the bounds of the set being modified, the value of  can approximate 0. The algorithm proposed by Islam et al. [11] for modification of inconsistent bounds can find out the most inconsistent bound. Then modify the lower bound or upper bound or both lower and upper bounds and calculate the value of a, if
can approximate 0. The algorithm proposed by Islam et al. [11] for modification of inconsistent bounds can find out the most inconsistent bound. Then modify the lower bound or upper bound or both lower and upper bounds and calculate the value of a, if , we repeat the steps below, otherwise we stop. Finally the consistent judgments are constructed. The steps are as follows:
, we repeat the steps below, otherwise we stop. Finally the consistent judgments are constructed. The steps are as follows:
Step 1. Calculate the expected weights of alternatives by (5). If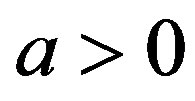 , then go to Step 2, otherwise stop.
, then go to Step 2, otherwise stop.
Step 2. Find out the matrices  and
and
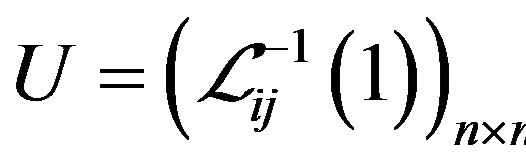 taking the lower and upper bounds from the
taking the lower and upper bounds from the , respectively.
, respectively.
Step 3. Bring the matrices 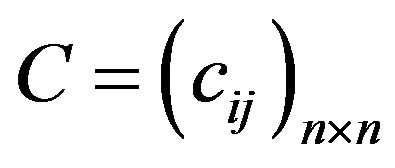 and
and 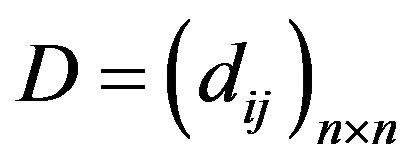 where
where
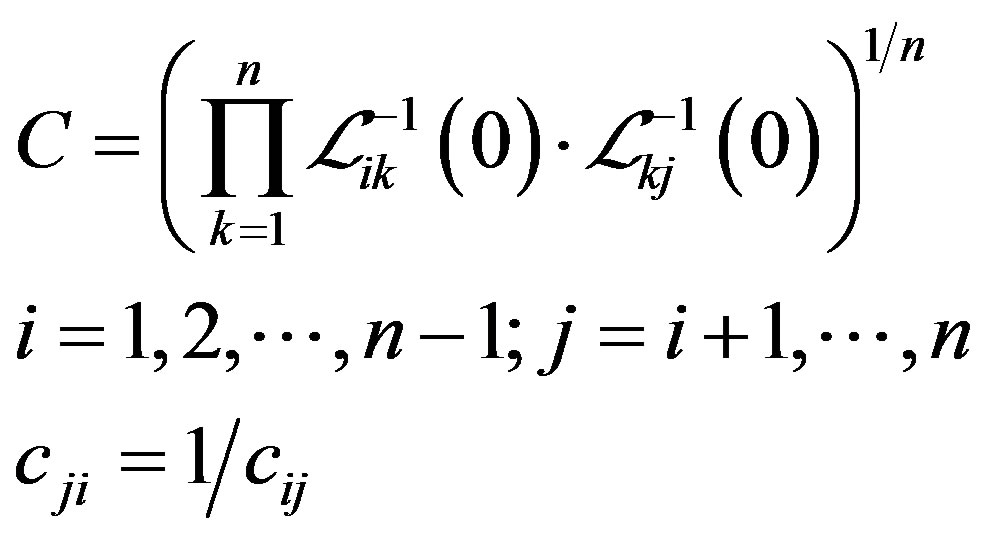
and
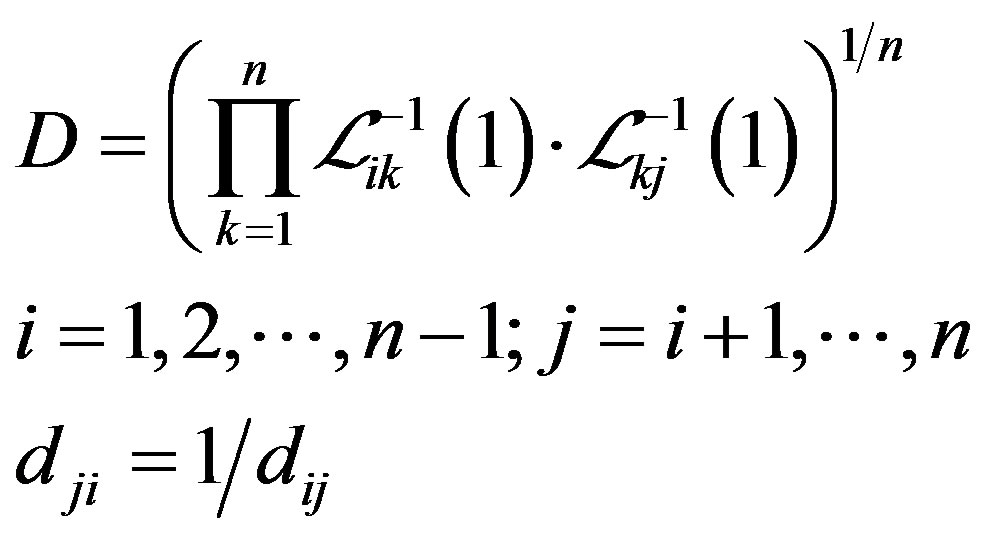
Four cases may appear,
(i) 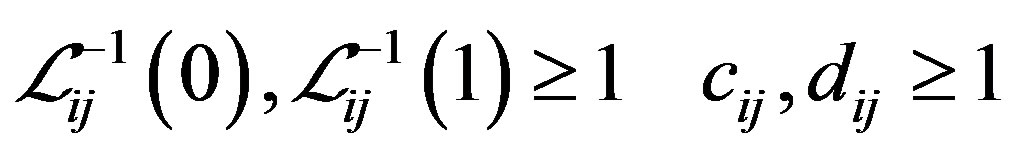
(ii) 
(iii) 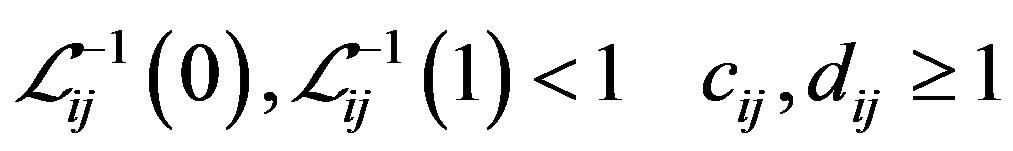
(iv) 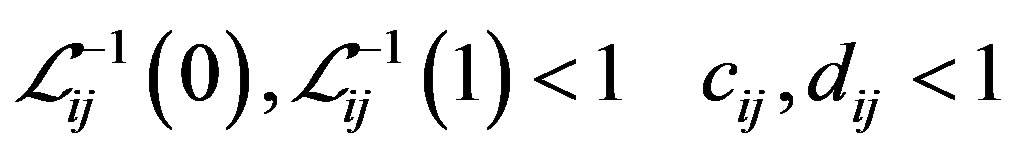
for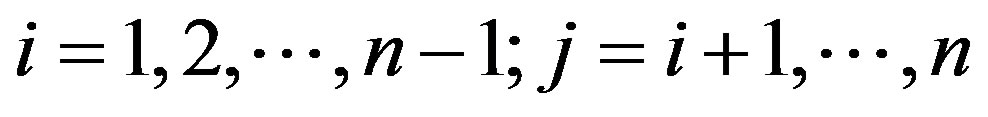 .
.
Step 4. Construct the matrices
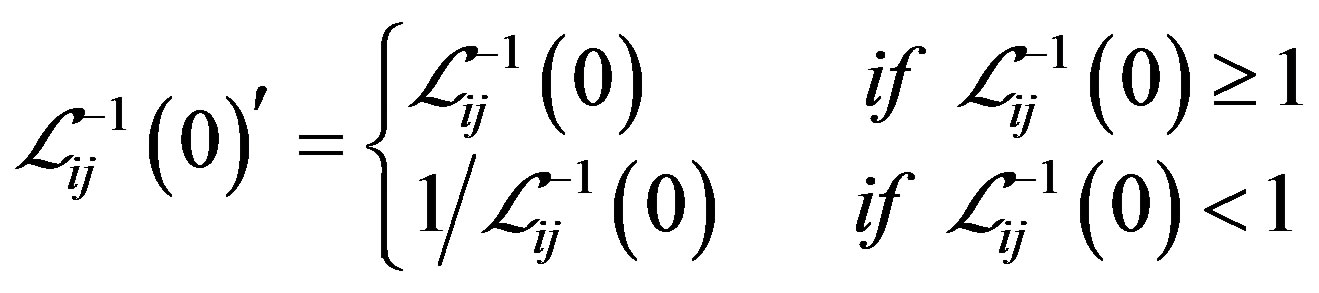
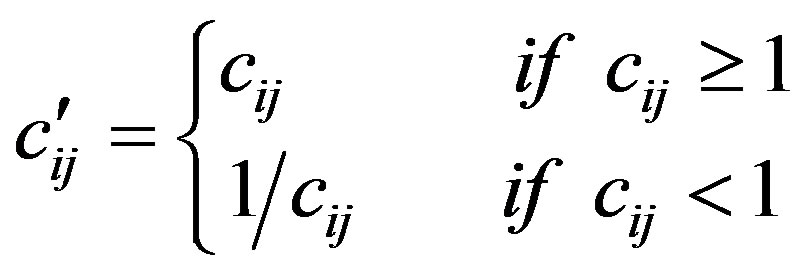
Same notations are used for the upper bound case.
Step 5. Calculate the absolute deviations
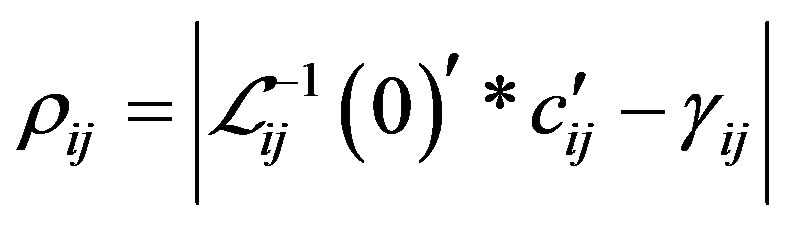 and
and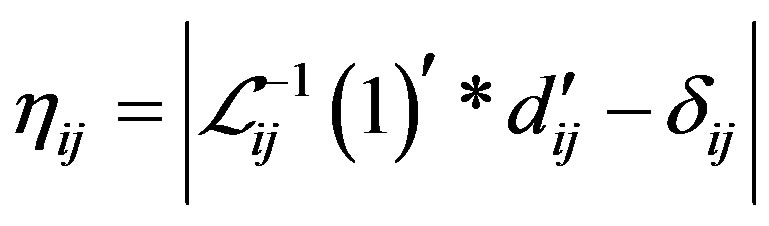 , for all
, for all 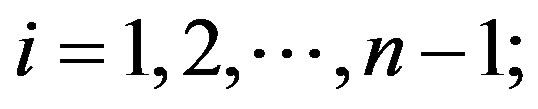
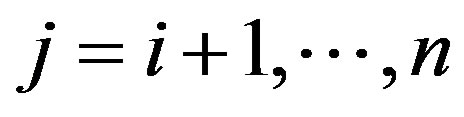 , where “*” denotes the “–” in cases (i) and (iv) and the “+” in cases (ii) and (iii) in Step 3.
, where “*” denotes the “–” in cases (i) and (iv) and the “+” in cases (ii) and (iii) in Step 3. 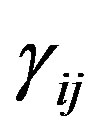 and
and 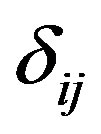 are 0 in cases (i) and (iv) and 2 in cases (ii) and (iii).
are 0 in cases (i) and (iv) and 2 in cases (ii) and (iii).
Step 6. Find out the maximum of all the deviations 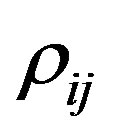 and
and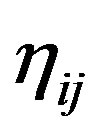 ,
,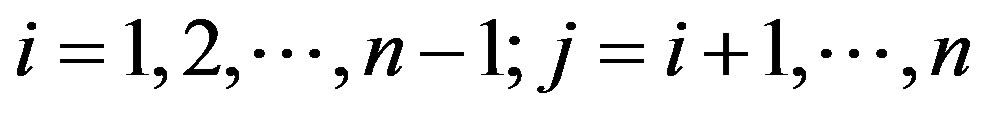 . If
. If 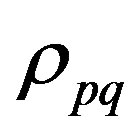 is maximum, then modify
is maximum, then modify , otherwise if
, otherwise if 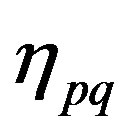 gives the maximum value, vary
gives the maximum value, vary . If
. If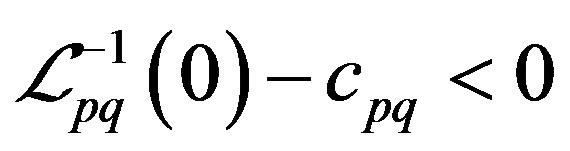 , then
, then 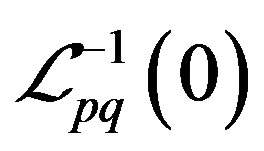 should be increased, otherwise the modified value should be decreased. Similar treatment follows for the matrix of upper bounds.
should be increased, otherwise the modified value should be decreased. Similar treatment follows for the matrix of upper bounds.
Go to Step 1.
After introducing the UVM and algorithm for modifycation of inconsistent bounds, we show the whole process below. The whole process introduced for generating uncertainty weights and expected weights from uncertainty comparison matrices is summarized in Figure 1.
4. NUMERICAL EXAMPLES
In this section, we offer three numerical examples that
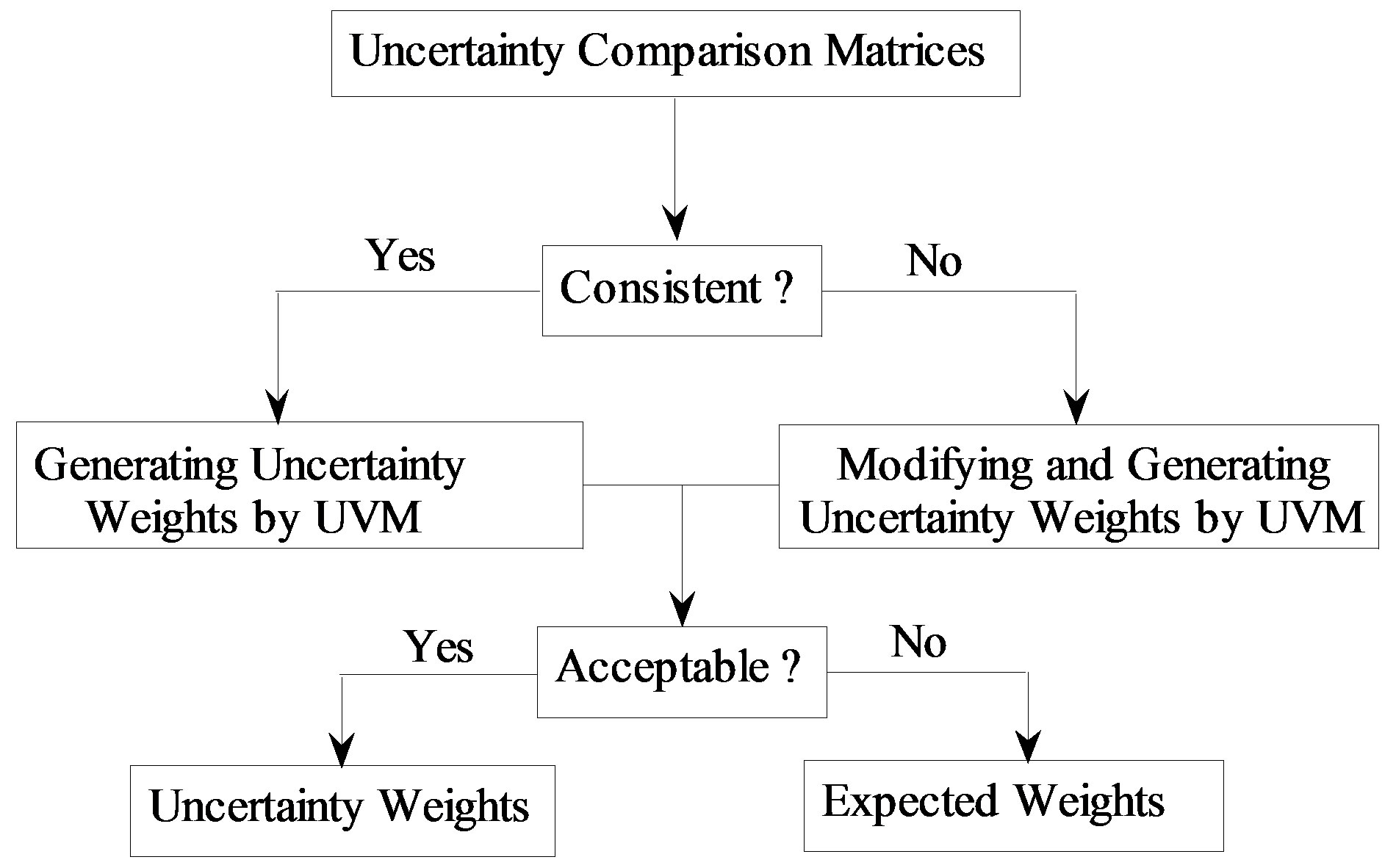
Figure 1. Process for generating priorities from uncertainty comparison matrices.
are examined using the proposed UVM and modification algorithm and show their applications. The uncertainty distributions are obtained by Delphi method. Some comparisons with other existing methods will be made whenever necessary.
Example 1 Consider the following interval comparison matrix that was examined by Arbel and Vargas [22] and Wang et al. [13].
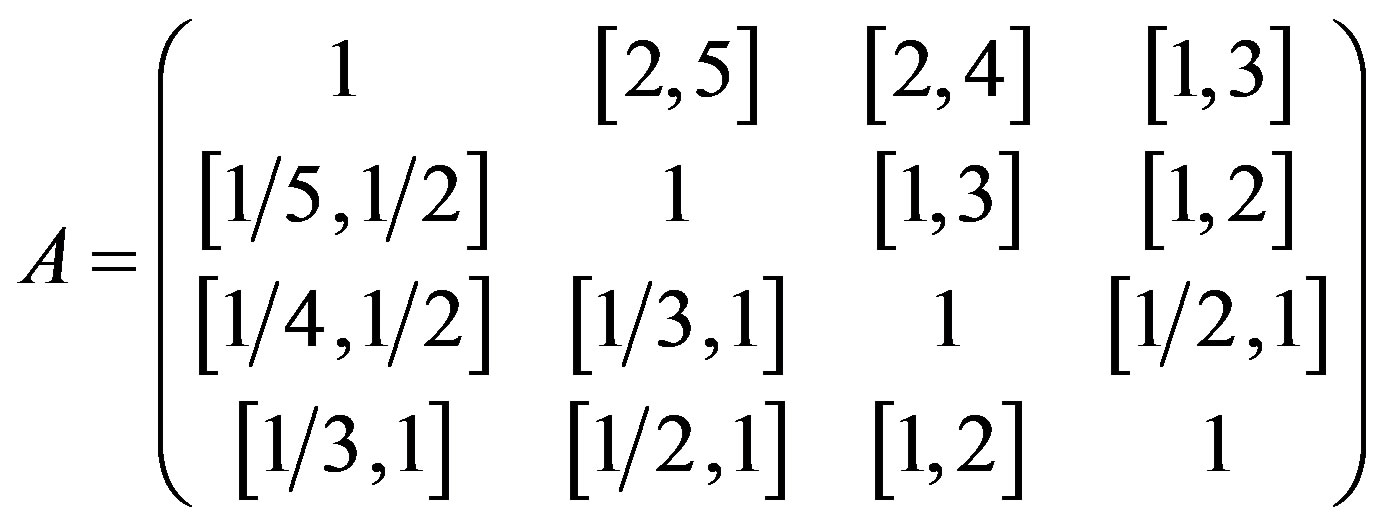
It has been known that  is a consistent interval judgments matrix, which was confirmed using the goal programming model given by Wang et al. [13]. Subsequently Wang et al. derived the interval weights and ranking by two-stage logarithmic goal programming method
is a consistent interval judgments matrix, which was confirmed using the goal programming model given by Wang et al. [13]. Subsequently Wang et al. derived the interval weights and ranking by two-stage logarithmic goal programming method
(TLGP),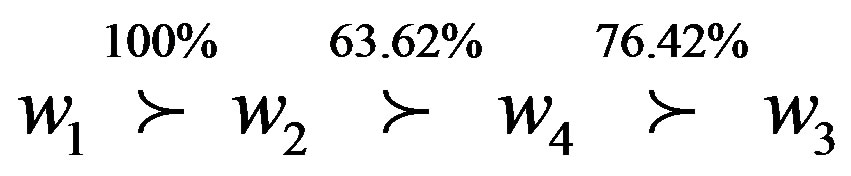 . The percentage is called degree of preference which represents criterion
. The percentage is called degree of preference which represents criterion  is preferred over criterion
is preferred over criterion . We can find out that the interval comparison matrices can be transformed easily into uncertainty comparison matrices as given in Eq.1, so the corresponding uncertainty comparison matrix of
. We can find out that the interval comparison matrices can be transformed easily into uncertainty comparison matrices as given in Eq.1, so the corresponding uncertainty comparison matrix of  is
is

Before testing the consistency of , we should derive the expected values of uncertainty weights using Eq.5. So the normalized expected values of uncertainty weights are
, we should derive the expected values of uncertainty weights using Eq.5. So the normalized expected values of uncertainty weights are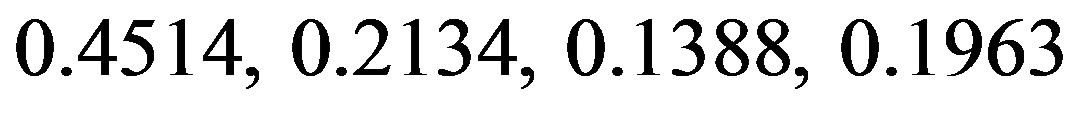 . Using the formula Eq.10,
. Using the formula Eq.10, 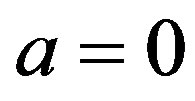 is obtained and
is obtained and  is consistent uncertainty comparison matrix. So we can directly use the UVM. By the Eqs.2 and 4, Table 1 shows the
is consistent uncertainty comparison matrix. So we can directly use the UVM. By the Eqs.2 and 4, Table 1 shows the
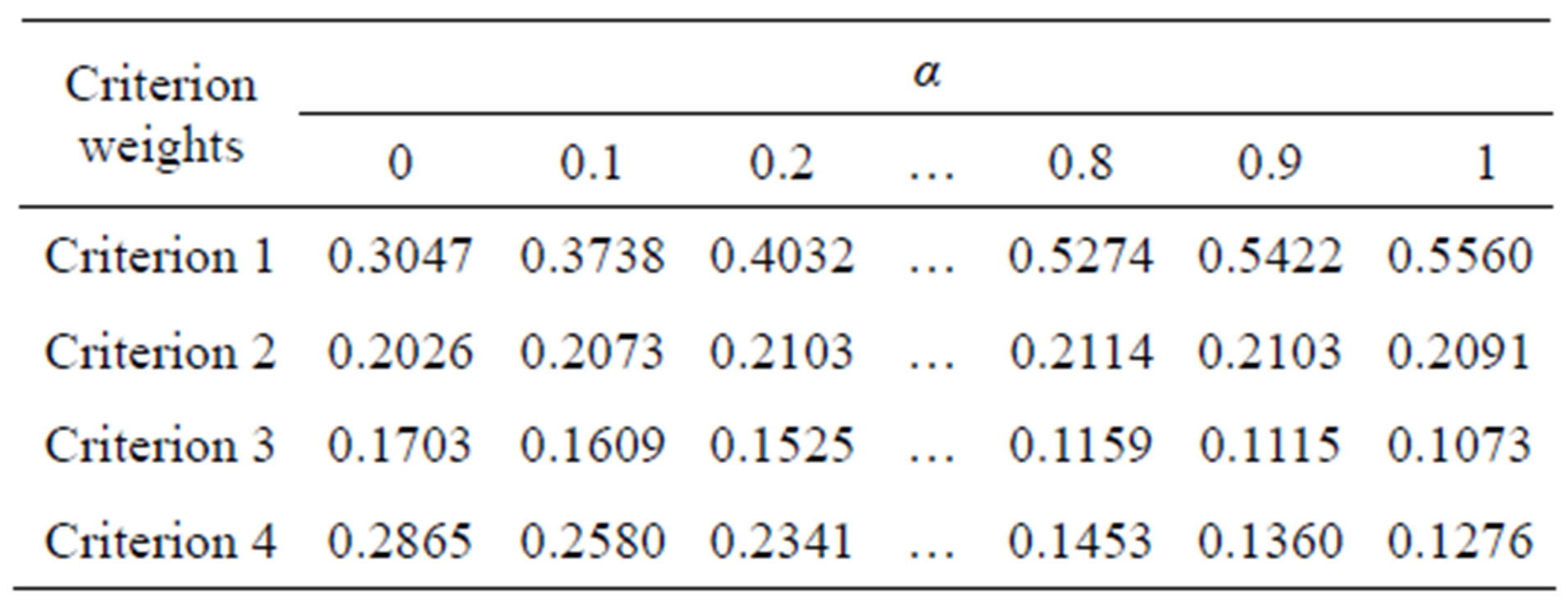
Table 1. Uncertainty weights in Example 1.
weights with different uncertain measures, from which it is clear that criterion 1 is the most important because its weight is greater than weights of all the other criteria with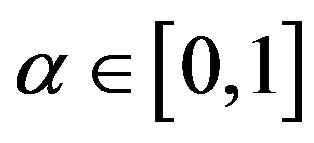 . To provide a complete ranking order for the four uncertainty weights, a directed diagram is depicted in Figure 2, from which it is quite clear that the ranking order is generated to be
. To provide a complete ranking order for the four uncertainty weights, a directed diagram is depicted in Figure 2, from which it is quite clear that the ranking order is generated to be 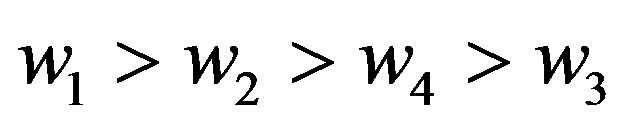
 , which is same as rankings given by Wang et al. [13] using TLGP, but our ranking order provides the information about uncertain measure of preference, which reflects uncertain nature of the ranking. We can say that the ranking is credible.
, which is same as rankings given by Wang et al. [13] using TLGP, but our ranking order provides the information about uncertain measure of preference, which reflects uncertain nature of the ranking. We can say that the ranking is credible.
Example 2 Consider the following decision analysis given by interval comparison matrix, which was investigated by Kress [10], Islam et al. [11] and Wang et al. [9]
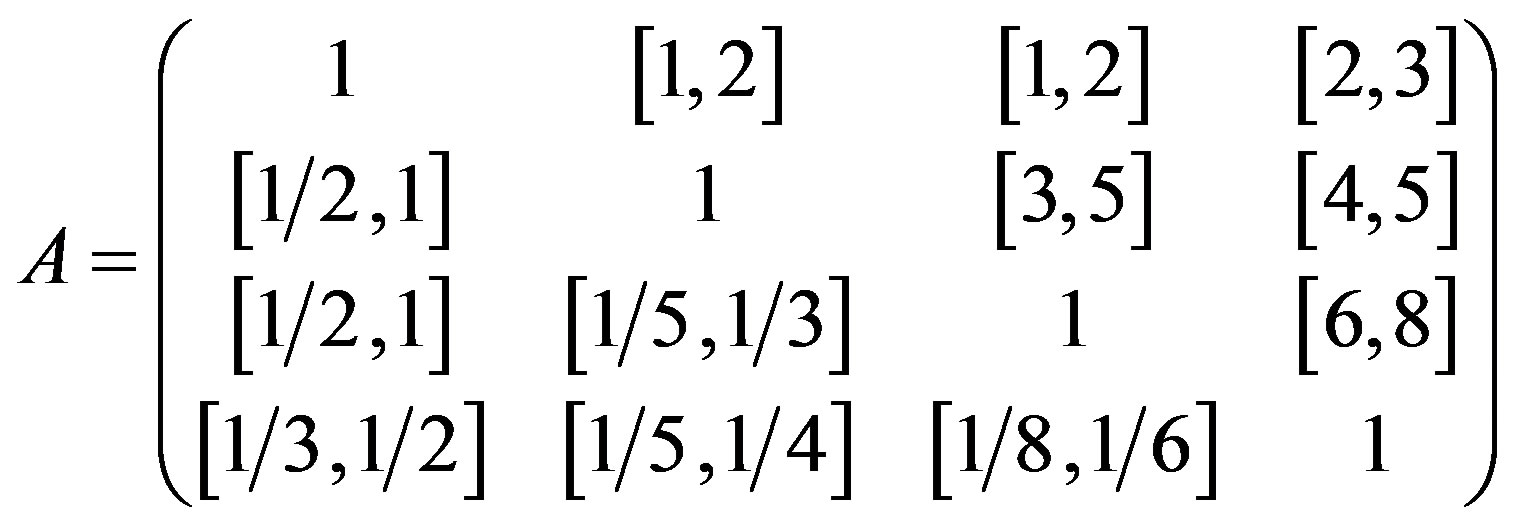
Naturally, the uncertainty comparison matrix can be expressed as

Kress [10] and and Islam et al. [11] showed that this interval comparison matrix A is inconsistent, which can be further confirmed using the algorithm proposed above. The problem of weight determination from  is calculated expected weights are (0.3150, 0.3922, 0.2226, 0.0701), respectively, with
is calculated expected weights are (0.3150, 0.3922, 0.2226, 0.0701), respectively, with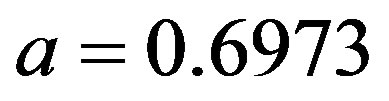 . Using the UVM proposed in Section 2, the preference relations without modification can be obtained and plotted in Figure 3.
. Using the UVM proposed in Section 2, the preference relations without modification can be obtained and plotted in Figure 3.
Since the value of  is positive, we apply the algorithm for identification of the inconsistent bounds. The maximum values among all ρij and ηij are
is positive, we apply the algorithm for identification of the inconsistent bounds. The maximum values among all ρij and ηij are  and
and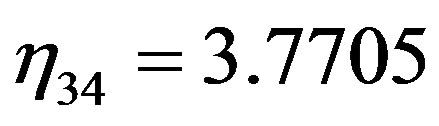 , respectively. Perhaps the experts gave the judgment
, respectively. Perhaps the experts gave the judgment 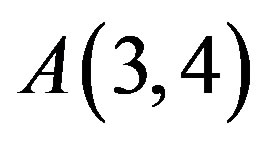 carelessly. Changing this judgment
carelessly. Changing this judgment  to
to  the modified set of weights as (0.3246, 0.4042, 0.1773, 0.0939) with
the modified set of weights as (0.3246, 0.4042, 0.1773, 0.0939) with 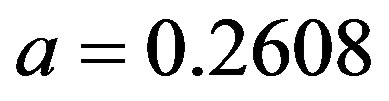 can be got. Since
can be got. Since  is still positive, we compute the
is still positive, we compute the
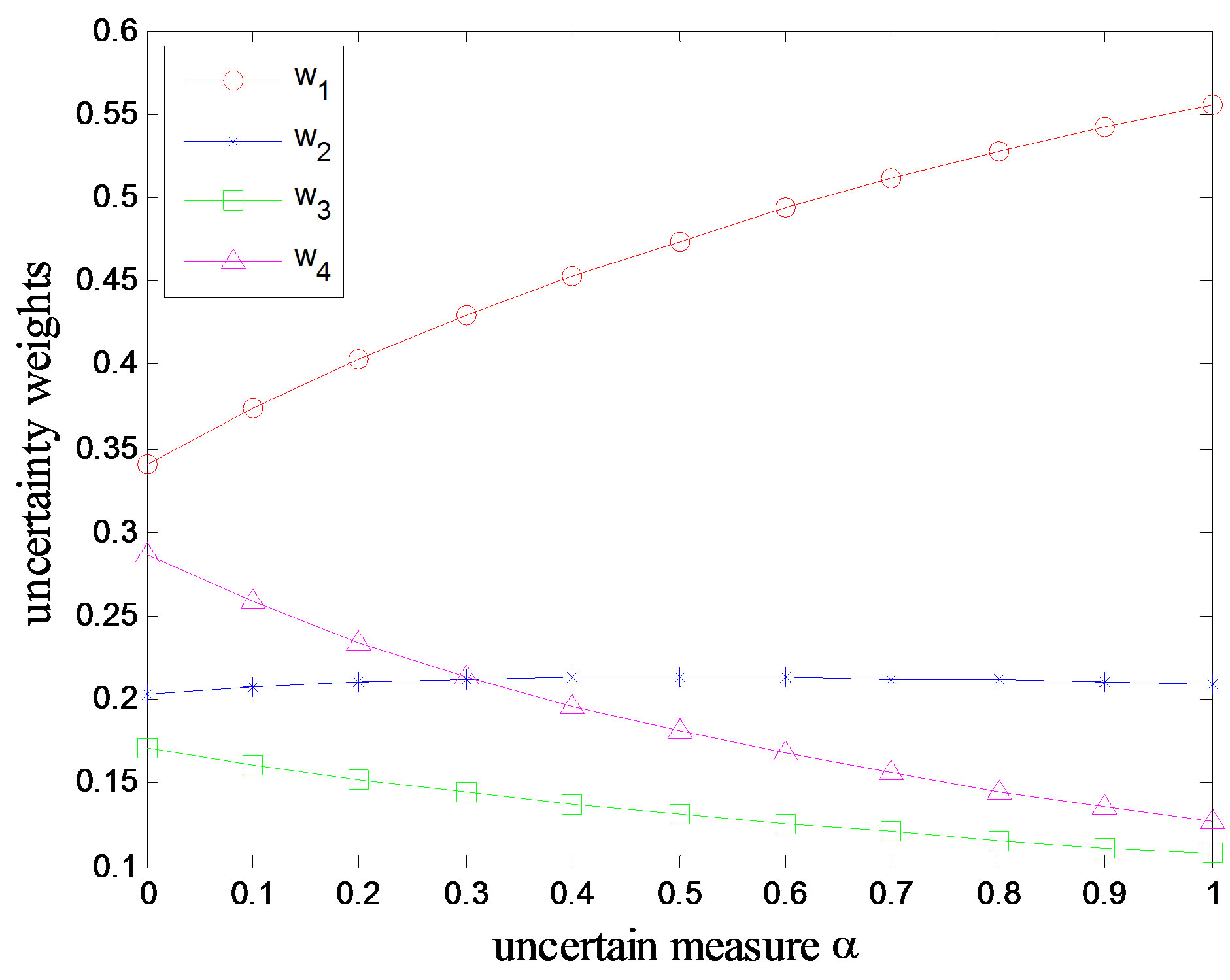
Figure 2. Preference relations in Example 1.
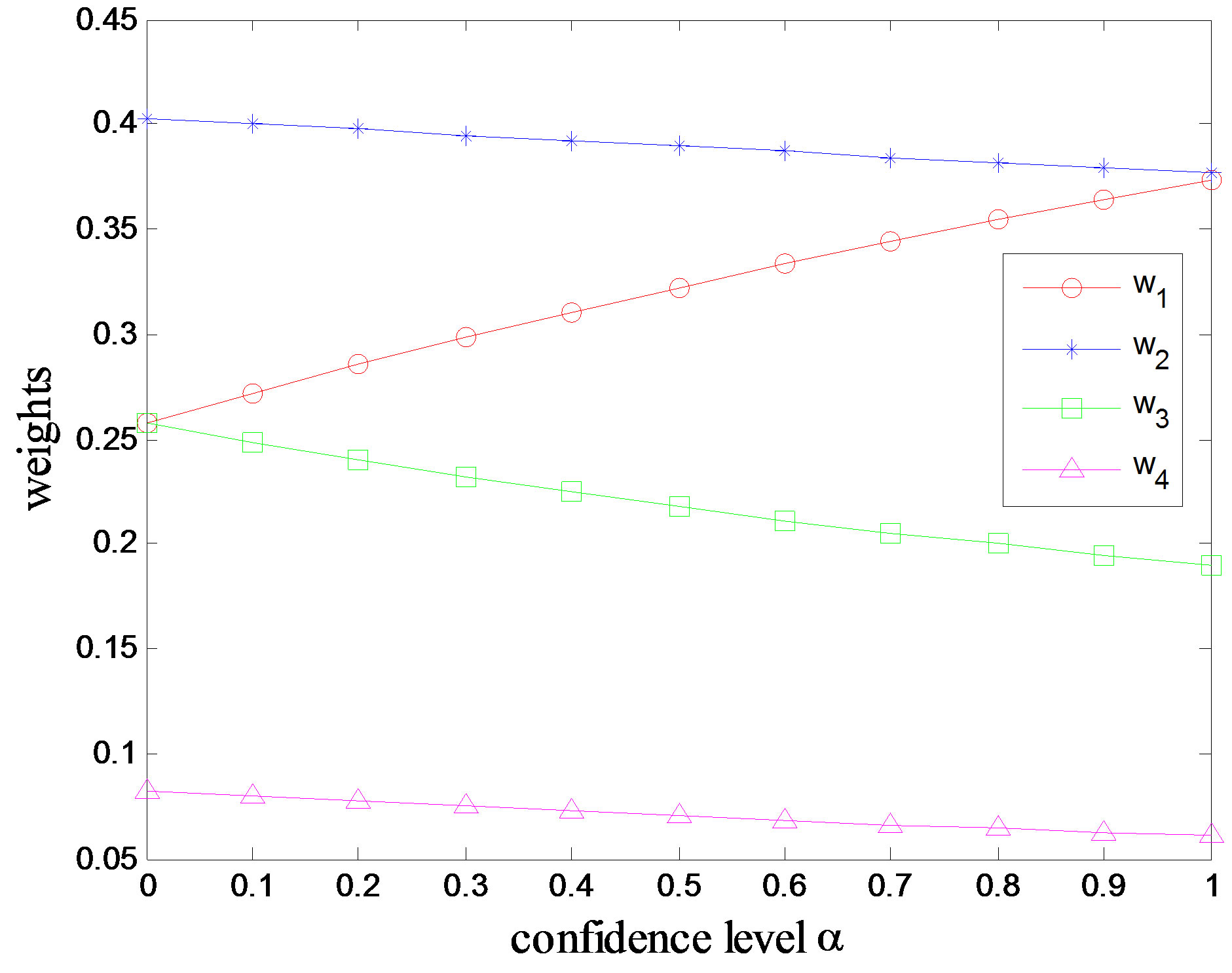
Figure 3. Preference relations without modification in Example 2.
deviationsρij and ηij and it is found that 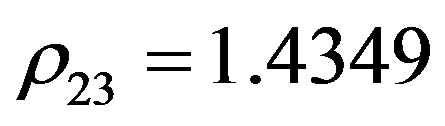 and
and  are the maximum among the deviations. We take the new bounds
are the maximum among the deviations. We take the new bounds 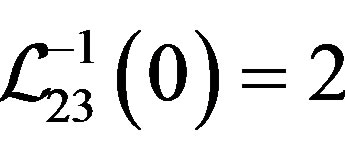 and
and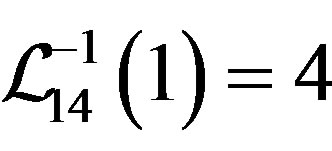 . Repeating the steps above, the final modified set of expected weights are obtained as (0.3469, 0.3452, 0.2243, 0.0836) with
. Repeating the steps above, the final modified set of expected weights are obtained as (0.3469, 0.3452, 0.2243, 0.0836) with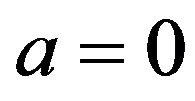 . The modified uncertainty comparison is
. The modified uncertainty comparison is
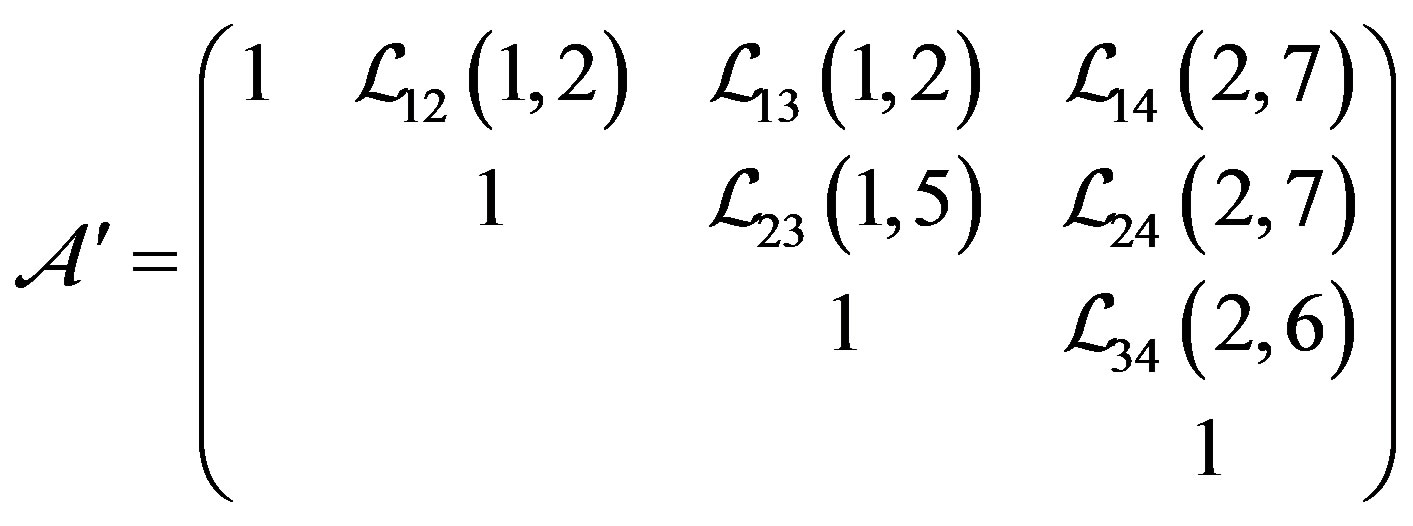
Until now we can apply the UVM to calculate the uncertainty weights with different uncertain measures and the results are recorded in Table 2. A directed diagram is depicted in Figure 4, from which it is quite clear that the ranking order is given by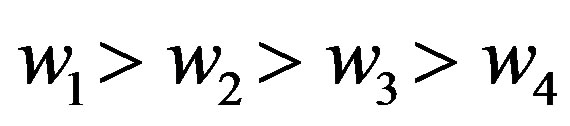 ,
, 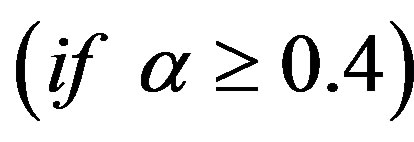 which is different from the preference relations without
which is different from the preference relations without

Table 2. Modified uncertainty weights in Example 2.
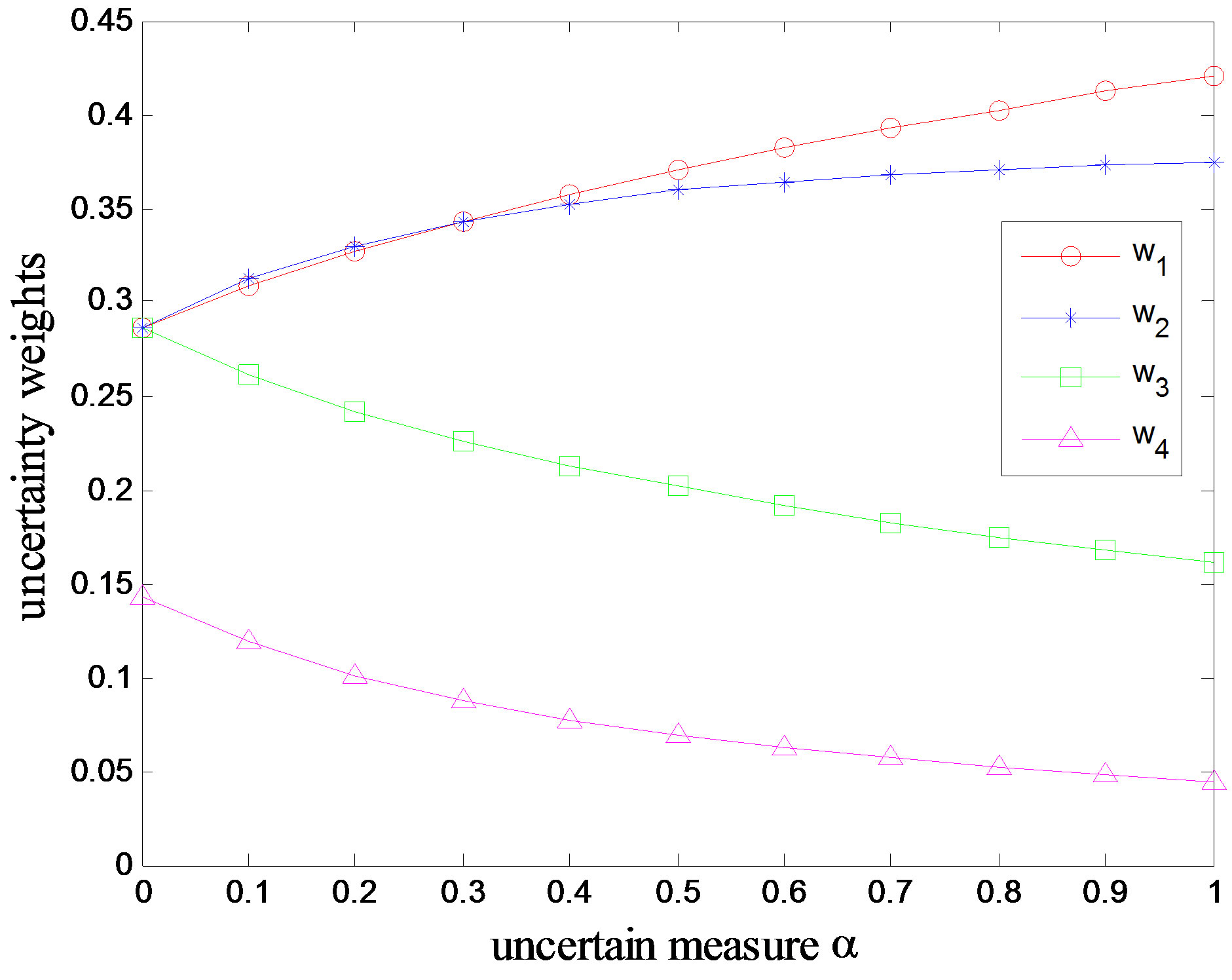
Figure 4. Modified preference relations in Example 2.
modification. Islam et al. [11] gave the ranking 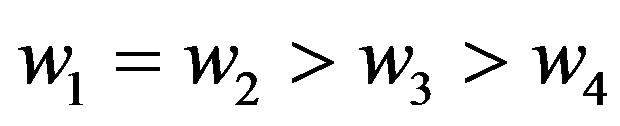 . In Islam’s lexicographic goal programming (LGP) method, the upper triangular judgments of
. In Islam’s lexicographic goal programming (LGP) method, the upper triangular judgments of  are used for priorities. However the lower triangular judgments of
are used for priorities. However the lower triangular judgments of  are applied, which provide completely the same information, then a different point estimate would be obtained. It is likely to be flawed. Wang et al. [13] showed the final ranking
are applied, which provide completely the same information, then a different point estimate would be obtained. It is likely to be flawed. Wang et al. [13] showed the final ranking
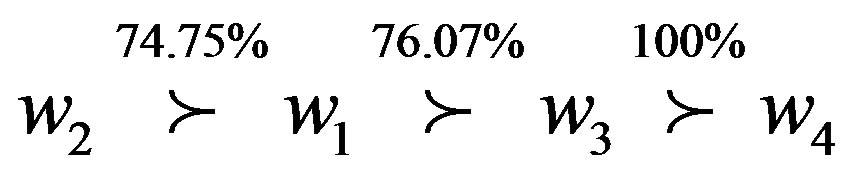 . In that TLGP method, the ranks of alternatives is based on inconsistent interval comparison matrices and minimizing the deviation variables but no optimal minimum is given. We fail to rank the two alternatives when the degrees of preference are equal to 50%. The results given by TLGP are doubtful.
. In that TLGP method, the ranks of alternatives is based on inconsistent interval comparison matrices and minimizing the deviation variables but no optimal minimum is given. We fail to rank the two alternatives when the degrees of preference are equal to 50%. The results given by TLGP are doubtful.
Example 3 The problem is about a government agency’s goal (G) to rank chemicals A1, A2, A3 in terms of their level of harm to the environment. The goal is affected by three criteria with criterion C1: Air, C2: Water, and C3: Soil, see Figure 5.
The uncertainty distribution matrices for the three criteria as well and for the three alternatives are summarized in Table 3. Before checking the consistency of the matrices, we can not derive the priorities using any methods. However the expected weights can be obtained by Eq.5 and shown in Table 4, from which four uncertainty comparison matrices all turn out to be inconsistent.
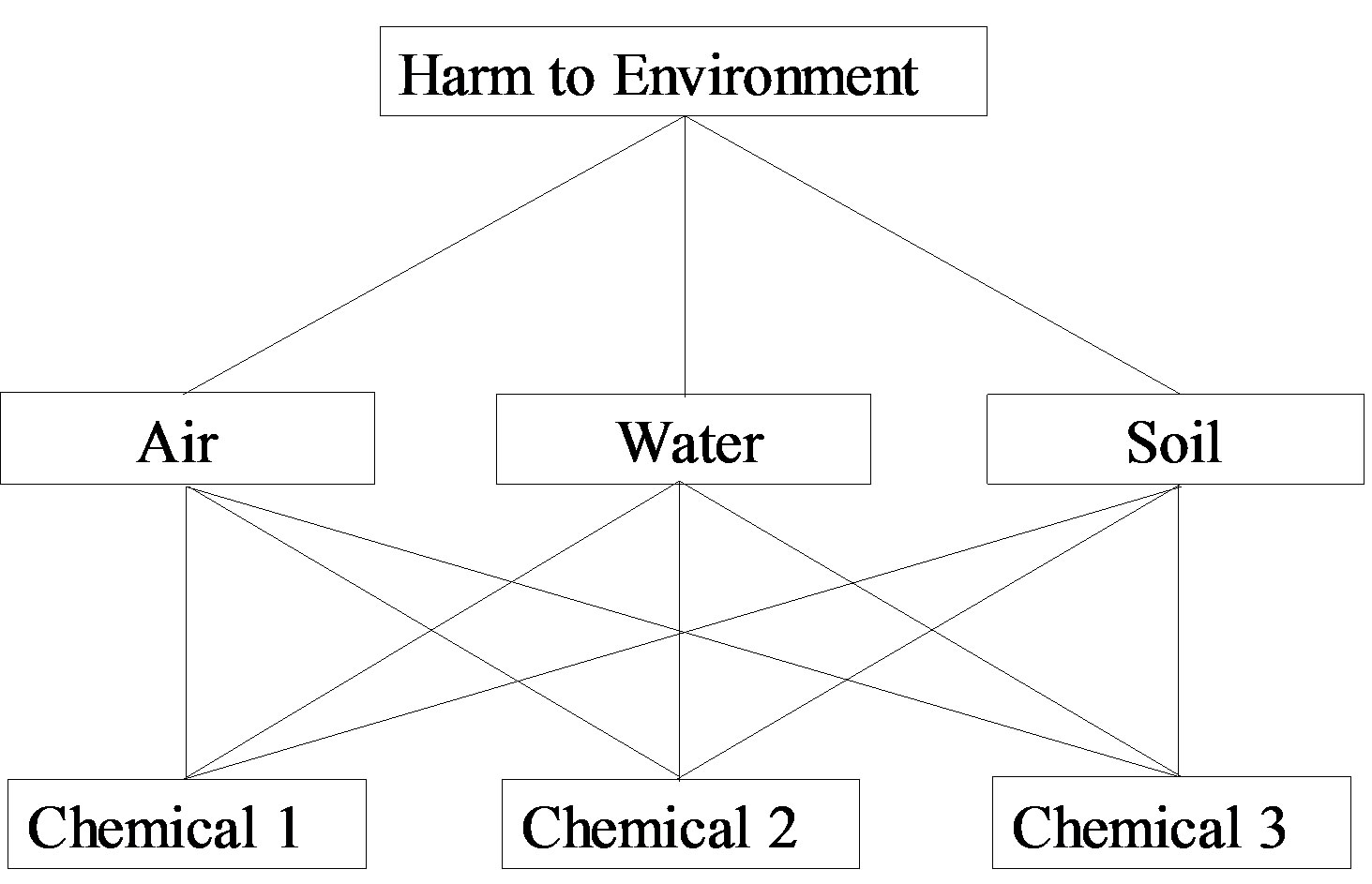
Figure 5. Hierarchy structure in Example 3.

Table 3. Uncertainty comparison matrices in Example 3.
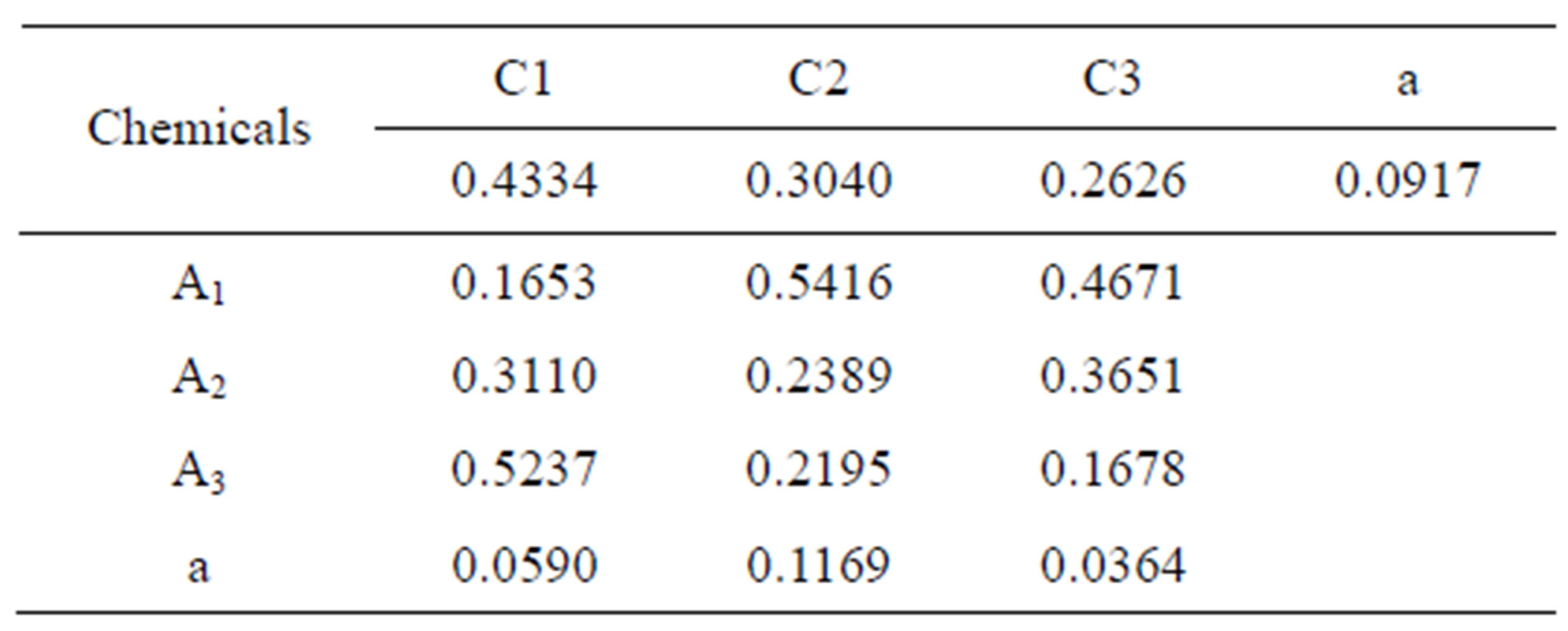
Table 4. Expected weights and deviation α in Example 3.
The proposed algorithm is used to modify the bounds of matrices and new uncertainty comparison matrices are recorded in Table 5. Table 6 gives both local and global expected weights. It is can be seen that the expected weights indicate the ranking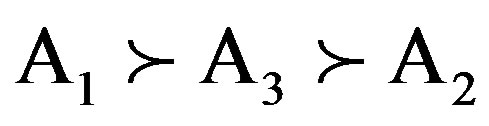 . Based on the consistent matrices, the UVM are used to generate the local and global priorities. In this paper,
. Based on the consistent matrices, the UVM are used to generate the local and global priorities. In this paper, 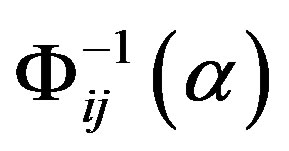 can be treated as precise number with
can be treated as precise number with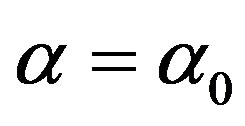 . So the synthesis of weights is similar with that in conventionalAHP. Comparisons with original matrices without modification are depicted in Figures 6 and 7.
. So the synthesis of weights is similar with that in conventionalAHP. Comparisons with original matrices without modification are depicted in Figures 6 and 7.
Note that, in Figure 7, the ranking alters with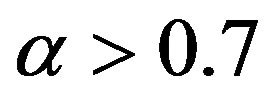 , which is unacceptable. It is clear that A1 is preferred over A2 and A3, but whether A3 is preferred over A2 is ambiguous. The reason may be that the consistent matrices include contradictory information. Kwiesielewicz and Van Uden [23] considered that the consistency test is performed to ensure that judgments are neither random nor illogical. They pointed out that even if a matrix will pass a consistency check successfully, it can be
, which is unacceptable. It is clear that A1 is preferred over A2 and A3, but whether A3 is preferred over A2 is ambiguous. The reason may be that the consistent matrices include contradictory information. Kwiesielewicz and Van Uden [23] considered that the consistency test is performed to ensure that judgments are neither random nor illogical. They pointed out that even if a matrix will pass a consistency check successfully, it can be

Table 5. Modified uncertainty comparison matrices in Example 3.
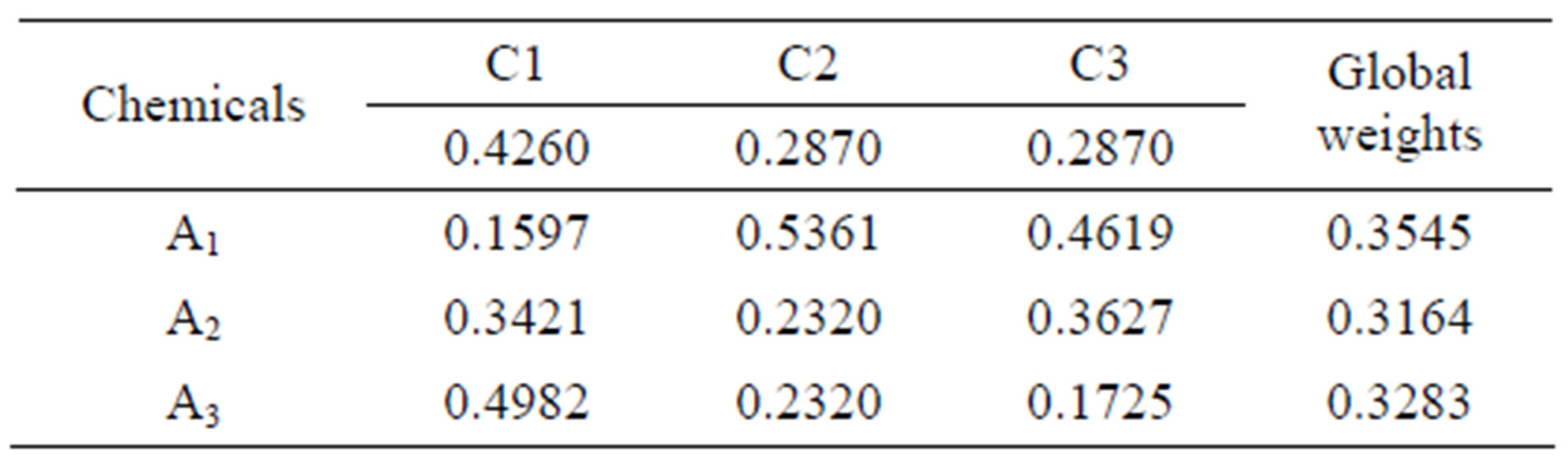
Table 6. Local expected weights and global expected weights in Example 3.
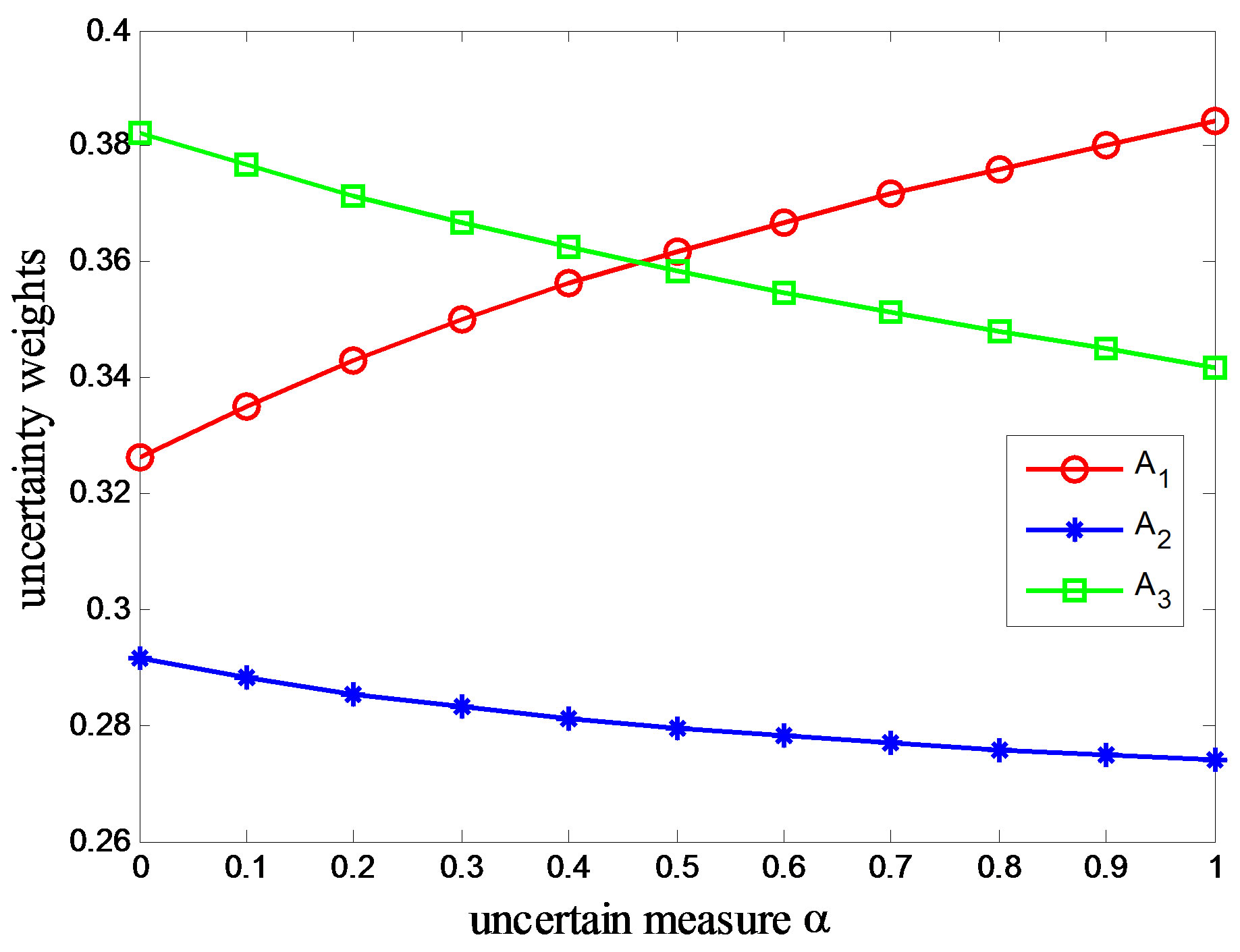
Figure 6. Preference relations without modification in Example 3.
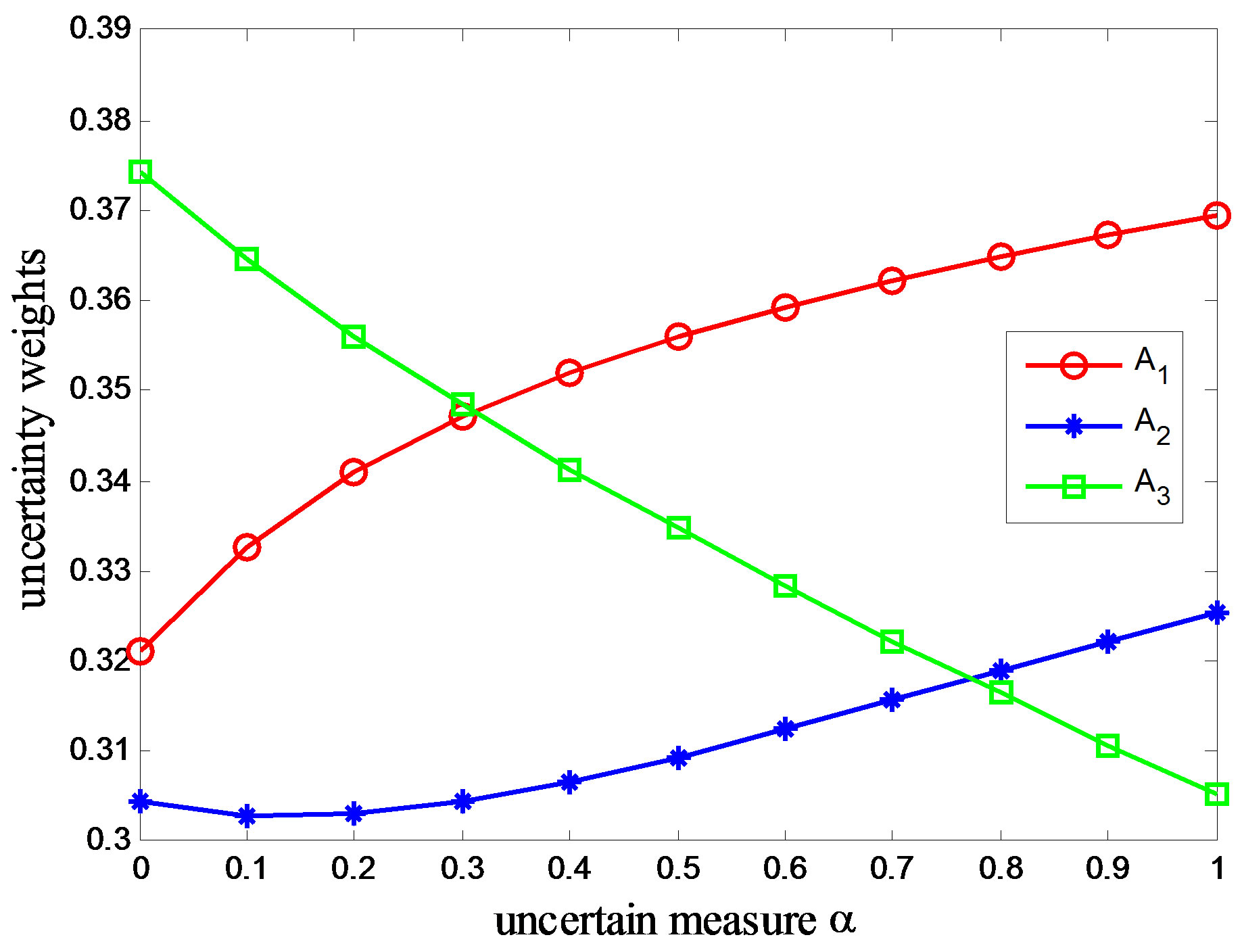
Figure 7. Modified preference relations in Example 3.
contradictory. Perhaps the judgments for A3 have been given carelessly. Without any new information, we take the ranking  given by expected weights as the final ranks of alternatives.
given by expected weights as the final ranks of alternatives.
5. SUMMARY AND CONCLUDING REMARKS
In multiple criteria decision analysis problem, human judgments are required in order to generate relative weights of criteria. Due to complexity of real world decision problems and subjective nature of human judgments, uncertainty comparison matrices can provide a more realistic framework to explain such uncertainty. However how to check contradictions and avoid modified bounds exceeding the bounded 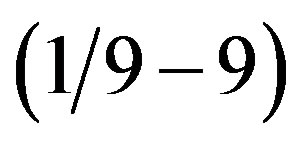 ratio scale are still subject to further investigation.
ratio scale are still subject to further investigation.
In this paper, uncertain variable method (UVM), a new approach to consistency and inconsistency of uncertainty comparison matrices was proposed to generate uncertainty weights. The definition of consistency for uncertainty comparison matrices was provided and a simple yet pragmatic approach for testing whether or not an uncertainty comparison matrix is consistent was put forward without having to solve any optimization model. In case of consistent uncertainty comparison matrices, the UVM was recommended to generate consistent uncertainty weights; otherwise the uncertainty comparison matrices would be modified via the algorithm proposed and the uncertainty weights were derived from modified matrices. We consider the uncertainty weights as final ranking if they were acceptable. Otherwise the ranks of expected weights would be adopted. Three numerical examples illustrated the simplicity and wide applicability of the proposed methods. Since interval comparison matrices may be transformed into uncertainty comparison matrices, the proposed methods are applicable to interval comparison matrices. Therefore they can be widely used to deal with decision analysis problems.
REFERENCES
- Saaty, T.L. (1977) A scaling method for priorities in hierarchical structures. Journal of Mathematical Psychology, 15, 234-281. doi:10.1016/0022-2496(77)90033-5
- Van Laarhoven, P.J.M. and Pedrycz, W. (1983) A fuzzy extension of Saaty’s priority theory. Fuzzy Sets and Systems, 11, 229-241.
- Buckley, J.J. (1985) Fuzzy hierarchical analysis. Fuzzy Sets and Systems, 17, 233-247. doi:10.1016/0165-0114(85)90090-9
- Boender, C.G.E., De Graan, J.G. and Lootsma, F.A. (1989) Multicretia decision analysis with fuzzy pairwise comparisons. Fuzzy Sets and Systems, 29, 133-143. doi:10.1016/0165-0114(89)90187-5
- Kwiesielewicz, M. (1998) A note on the fuzzy extension of Saaty’s priority theory. Fuzzy Sets and Systems, 95, 161-172. doi:10.1016/S0165-0114(96)00329-6
- Leung, L.C. and Cao, D. (2000) On consistency and ranking of alternatives in fuzzy AHP. European Journal of Operational Research, 124, 102-113. doi:10.1016/S0377-2217(99)00118-6
- Xu, Z.S. and Da, Q.L. (2005) A least deviation method to obtain a priority vector of a fuzzy preference relation. European Journal of Operational Research, 164, 206- 216. doi:10.1016/j.ejor.2003.11.013
- Saaty, T.L. and Vargas, L.G. (1987) Uncertainty and rank order in the analytic hierarchy process. European Journal of Operational Research, 32, 107-117. doi:10.1016/0377-2217(87)90275-X
- Arbel, A. (1989) Approximate articulation of preference and priority derivation. European Journal of Operational Research, 43, 317-326. doi:10.1016/0377-2217(89)90231-2
- Kress, M. (1991) Approximate articulation of preference and priority derivation—A comment. European Journal of Operational Research, 52, 382-383. doi:10.1016/0377-2217(91)90174-T
- Islam, R., Biswal, M.P. and Alam, S.S. (1997) Preference programming and inconsistent interval judgments. European Journal of Operational Research, 97, 53-62. doi:10.1016/S0377-2217(95)00377-0
- Haines, L.M. (1998) A statistical approach to the analytic hierarchy process with interval judgments. (I). Distributions on feasible regions. European Journal of Operational Research, 110, 112-125. doi:10.1016/S0377-2217(97)00245-2
- Wang, Y.M., Yang, J.B. and Xu, D.L. (2005) A two-stage logarithmic goal programming method for generating weights from interval comparison matrices. Fuzzy Sets and Systems, 152, 475-498. doi:10.1016/j.fss.2004.10.020
- Juan, A. and José María, M.-J. (2003) The geometric consistency index: Approximated thresholds. European Journal of Operational Research, 147, 137-145. doi:10.1016/S0377-2217(02)00255-2
- Wang, Y.M., Yang, J.B. and Xu, D.L. (2005) Interval weight generation approaches based on consistency test and interval comparison matrices. Applied Mathematics and Computation, 167, 252-273. doi:10.1016/j.amc.2004.06.080
- Liu, B.D. (2007) Uncertainty theory. 2nd Edition, Springer-Verlag, Berlin.
- Liu, B.D. (2010) Uncertainty theory: A branch of mathematics for modeling human uncertainty. Springer-Verlag, Berlin.
- Liu, B.D. (2010) Uncertainty theory. 4th Edition, Springer-Verlag, Berlin. doi:10.1007/978-3-642-13959-8
- Wang, C., Lin, L. and Liu, J.J. (2012) Uncertainty weight generation approach based on uncertainty comparison matrices. Applied Mathematics, 3.
- Crawford, G. and Williams, C. (1985) A note on the analysis of subjective judgment matrices. European Journal of Operational Research, 29, 387-405.
- Liu, Y.H. and Ha, M.H. (2010) Expected value of function of uncertain variables. Journal of Uncertain Systems, 4, 181-186.
- Arbel, A. and Vargas, L.G. (1993) Preference simulation and preference programming: Robustness issues in priority deviation. European Journal of Operational Research, 69, 200-209. doi:10.1016/0377-2217(93)90164-I
- Kwiesielewicz, M. and Van Uden, E. (2004) Inconsistent and contradictory judgments in pairwise comparison method in the AHP. Computers and Operations Research, 31, 713-719. doi:10.1016/S0305-0548(03)00022-4
NOTES
*This research was supported by the Guangxi Natural Science Foundation of China under the Grant No. 2011GXNSFA018149, Innovation Project of Guangxi Graduate Education under the Grant No. 2011105960202M31.

