Health
Vol.09 No.03(2017), Article ID:74888,14 pages
10.4236/health.2017.93036
Reliability of Blood Pressure Measurements: An Analysis of the White Coat Effect and Its Fluctuations
Kazumitsu Nawata1, Moriyo Kimura2
1Graduate School of Engineering, University of Tokyo, Tokyo, Japan
2The Public Health Institute, Tokyo, Japan
Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: February 24, 2017; Accepted: March 21, 2017; Published: March 24, 2017
ABSTRACT
In this paper, we evaluate the difference between the first and second measurements of blood pressure (BP) when BP is measured twice using the results of 17,775 medical checkups. The two measurements for both systolic BP (SBP) and the diastolic BP (DBP) fluctuated a large amount even though they were measured at a short interval. The first measurements were 6.7 and 2.4 mmHg higher than the second ones for SBP and DBP, suggesting a white coat effect. Then, the factors that might affect the differences between the two measurements were analyzed by the regression models. For both SBP and DBP, the difference increased as the first measurement increased. Age, gender, BMI and alcohol consumption were other important factors affecting the difference. In the case of a typical male individual, the typical criteria for hypertension of 140/90, 160/100 and 180/110 mmHg criteria in the first measurement would correspond to 135/86, 150/94 and 165/102 mmHg in the second measurement. The necessity of developing accurate and cost-efficient BP measurement methods is strongly suggested.
Keywords:
Blood Pressure Measurement, Hypertension, White Coat Effect, Medical Checkup, Fluctuation of Blood Pressure

1. Introduction
As the World Health Organization (WHO) [1] has pointed out, high blood pre- ssure (BP) or hypertension is one of the most important health factors overall and is an important risk factor of cardiovascular diseases [2] [3] [4] [5] . Therefore, it is very important that the BP will be correctly measured. Manual office BP (MOBP) is usually used to measure BP [6] , but there are questions about its reliability. One well-known problem is white coat hypertension (WCH) or white coat effects (WCE), in which the BP of an individual becomes higher than his/her normal level when BP is measured at an office, hospital or clinic, due to the stressfulness of the measurement. The other problem is measurement error; measuring BP should be done carefully by proper procedures [7] . Omiboni et al. [8] measured the BP in 14,143 patients from 27 countries. They found that 24-hour ambulatory BP monitoring (24-h ABPM) was significantly lower than office BP for both systolic BP (SBP) and diastolic BP (DBP). Although 140/70 mmHg for MOBP and 130/80 mmHg for 24-h ABPM criteria were used for hypertension, they also discovered that i) the prevalence of MOBP hypertension was higher than that of ABPM, and ii) WCH was more common than masked hypertension (elevated 24-h ABPM and normal office BP). Almedia et al. [9] reported the BP of 175 normotensives (NT), 316 WCH and 691 sustained hypertensives (SHT) by various measurement methods. The mean values of office BP (mmHg) were: SBP 125 and DBP 79 for NT; SBP 146 and DBP 91 for WCH; and SBP 143 and DBP 87 for SHT. However, the means of 24-h AMBP (mmHg) were SBP 119 and DBP 71 for NT; SBP 120 and DBP 73 for WCH; and SBP 120 and DBP 72 for SHT. There were large differences among subsequent measurements of office BP but very little difference among 24-h AOBP; however, Bastos [10] suggested that further studies were necessary to confirm their results. Cheng et al. [11] reported that central aortic was better than manual BP in predicting cardiovascular outcomes. Although other BP measurements such as 24-h ABPM may be better predictors of cardiovascular events than conventional office BP measurement [12] [13] [14] , these methods can be costly to implement. Wohlfahrt et al. [15] recommended automated office BP (AOBP). They measured 2145 patients and found that manual SBP and DBP measurements were higher than those of AOBP. They concluded that “AOBP of 131/85 mmHg corresponds to the manual BP of 140/90 mmHg”. Another alternative is home BP monitoring. Arrieta et al. [16] concluded that the returns on a one-dollar investment in this technology would be from $7.50 to $19.34 in the long run. Moran et al. [17] studied the cost-effectiveness of hypertension therapy and concluded that controlling hyper- tension could be effective and cost-saving except for in women aged 35 - 44 with stage 1 hypertension and no cardiovascular disease [18] . However, the factors of individuals that may affect WCE were not analyzed in these studies.
The other important issue is whether WCH really affects health conditions or not and there have been intense debates about the prognostic significance of WCH compared with NT and SHT [9] [19] . Some studies have reported that patients with WCH had less damage to target organs than those with SHT [20] [21] [22] [23] [24] , while no difference was found between WCH and NT patients [25] . But others suggested that WCH is a risk factor [26] [27] . More recently, Franklin et al. [28] compared 653 subjects with WCH and 653 NT subjects by an age- and cohort-matching study. They concluded that the WCE is related to age, not cardiovascular disease risk in most subjects. (For comments on their study, see Mancia and Grassi [29] .) Manios et al. [30] surveyed a total of 1382 patients. They measured BP and common carotid intima-media thickness (CCA-IMT) and found that patients with isolated systolic/diastolic WCH had an intermediate risk between NT and SHT in terms of CCA-IMT.
Clearly, it is necessary to measure BP accurately to treat hypertension properly. However, BP measurement methods, such as 24-h ABPM, are expensive, and it is currently unrealistic to apply them to many individuals including normal and healthy ones. We still must largely depend on conventional MOBP measurements, and thus we must know the reliability of the measured values.
In Japan, most workers 40 or older are required to have medical checkups, including BP measurements, once a year by the Industrial Safety and Health Act [31] . Nawata et al. [32] evaluated the distributions of BP and the factors affecting BP using a dataset obtained from one health insurance society. They found that the factors affecting BP were age, gender, certain eating habits, daily activities, smoking, drinking alcohol, sleeping and wages. However, the WCE and fluctuations of measurements were not considered in their study. For some individuals, BP was measured twice in a single medical checkup within a short (usually less than 30-minute) interval.
In this study, we analyzed differences between two subsequent BP measurements using the results of 17,775 medical checkups (hereafter, checkups) at which two BP measurements were performed. First, we evaluated the distributions of differences in the two measurements. Then, the factors affecting the differences were analyzed using regression models.
2. Data and Distributions of Differences between the Two Measurements
The data used in this study were obtained from one health insurance association formed by one large Japanese corporation. The dataset includes 113,979 checkups of 48,022 individuals collected from April, 2013 to March, 2016, for details, see Nawata et al. [32] . Among these checkups, BP was measured twice for both SBP and DBP in 17,775 checkups (15.6% of all checkups). According to the rules and guidelines of the Ministry of Health, Labour and Welfare [33] , hospitals and clinics practicing checkups may choose to measure BP once or twice in a single check-up. These measurements give us important information about WCE and the fluctuations of BP. It is reasonable to assume that the stress caused by measurement is reduced in the second measurement because of the experience of the first measurement. This implies that, if WCE exists, a systematic bias would appear and the first measurement would be larger than the second one. Hence, we formed the hypothesis that the difference between the first and second measurements (= first-second; hereafter, “difference”) would be positive on average. If the difference is solely caused by measurement errors, however, the expected value would be zero. Note that we call a systematic bias in the two measurements the WCE and the other part of the difference (= difference − bias) the “measurement error”. The measurement error is caused by an improper measuring procedure and a ran- dom fluctuation of BP over time with a mean of zero.
Figure 1 shows the distribution of the first and second measurements of SBP, and Figure 2 shows the differences. The distribution is skewed toward the right. The first part of Table 1 is the summary. The ages of the individuals ranged from 39 to 74 years with mean 50.9 and standard deviation (SD) 7.4, and 14.7% were female. The first and second measurements and their difference were 141.1 ± 18.9, 134.5 ± 17.1 and 6.7 ± 9.9 mmHg, respectively (mean ± SD). The relative bias (= mean of differences/mean of the first measurements) is 4.7%. For the differences, 73.7% were positive, 21.6% were negative and 4.7% were unchanged. The t-value is 90.4 and the null hypothesis that the mean of the differences is zero is rejected by a reasonable level of significance. Moreover, 35.8% of the differences were 10 mmHg or greater while only 3.5% were −10 mmHg or less. In other words, our result supports the existence of WCE for SBP even if measurements were performed in a very short interval. Moreover, SD of the difference is almost 10 mmHg. This means that BP fluctuates a great deal for many individuals even within a short period.
Figure 3 and Figure 4 show distributions of the first and second measurements and their difference for DBP. The summary is given in the latter part of Table 1. The first and second measurements and their difference were 89.4 ± 12.6, 84.5 ± 11.8 and 2.4 ± 5.9 mmHg, respectively. Among the observations, 63.4% were positive, 27.6% were negative and 9.1% were unchanged. The t-value is 55.4 and
Figure 1. Distributions of first and second measurements (SBP).
Figure 2. Distribution of the difference (SBP).
Table 1. Summary of the first and second measurements and their difference.
SD: standard deviation, age: mean 50.9 and SD 7.4, female: 14.7%.
Figure 3. Distributions of first and second measurements (DBP).
Figure 4. Distribution of the difference (DBP).
the null hypothesis that the mean of the differences is zero is rejected by a reasonable level of significance, as in the case of SBP. However, the relative bias was 2.4%, which is about half that of the SBP case, and 32.3% of the differences were 5 mmHg or more while only 8.6% were −5 mmHg or less. This suggests that the WCE of DBP is weaker than that of SBP.
3. Factors Affecting the Difference
The analysis of the previous section suggests the existence of WCE. In this section, factors affecting the differences are analyzed by regression models for both SBP and DBP.
3.1. Difference of SBP
Figure 5 shows the relation of the first measurement and difference. There is a clear trend such that the difference is larger in patients with higher first measurements, with a correlation coefficient of 0.439. Therefore, we first evaluated the gross relation of the first measurement and difference by a regression model.
Model 1A:
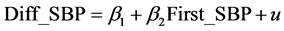 (1)
(1)
where First_SBP is the difference of SBP, First_SBP is the first measurement and 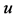 is an error term with mean of zero and
is an error term with mean of zero and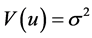 . The result of the estimation of Model 1A is given by
. The result of the estimation of Model 1A is given by
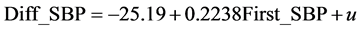 , R2 = 0.1882,
, R2 = 0.1882, (2)
(2)
(0.5001) (0.00352)
The standard errors (SE) are in parentheses. This means that the difference increases by 2.2 mmHg for each 10-mmHg increment of the first measurement.
Next, we consider the model including factors that may affect the difference. The model is given by
Model 1B:
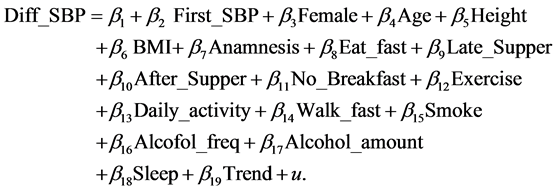 (3)
(3)
The explanatory variables other than First_SBP are the same as those used by Nawata et al. [32] and as follows: Female (male: 0, female: 1), Age, Height (cm), BMI (body mass index = weight (kg)/height (m)2), Anamnesis (1: with anamnesis; 0: otherwise), Eat_fast (1: eating faster than other people; 0: otherwise), Late_Supper (1: eating supper within two hours before bedtime three times or more in a week; 0: otherwise), After_supper (1: eating snacks after supper three times or more in a week, 0: otherwise), No_breakfast (1: not eating breakfast three times or more in a week; 0: otherwise), Exercise (1: doing exercise for 30
Figure 5. Relation of the first measurement and difference (SBP).
minutes or more twice or more in a week for more than a year; 0 otherwise), Daily_activity (1: doing physical activities (walking or equivalent) for one hour or more daily, 0: otherwise), Walk_fast (1: walking faster than other people of a similar age and the same gender; 0: otherwise), Smoke (1: smoking; 0: otherwise), Alcohol_freq (0: not drinking alcoholic drinks, 1: some-times, 2: everyday), Alcohol_amount (0: not drinking; 1: drinking less than 180 ml of Japanese sake wine (about a 15% alcohol percentage) or equivalent alcohol in a day when drinking; 2: drinking 180 - 360 ml; 3: drinking 360 - 540 ml; 4: drinking 540 ml or more), Sleep (1: sleeping well; 0: otherwise), and Trend, which is the time trend by year and given by (year of checkup 2013).
The results of 11,850 checkups without missing values for any of the explanatory variables were used in this model. The mean and SD of the dependent variable Diff_SBP were 5.6 and 9.6 mmHg. The mean and SD of First_SBP were 138.0 and 19.1 mmHg in this case. Female, Age and Height are basic characteristics of individuals, and 17.8% were female, means were 50.2 and 167.9 cm and SD are 7.2 and 7.7 cm for Age and Height, respectively. BMI and Anamnesis represented the current obesity and health conditions with mean and SD of 24.3 and 3.96 for BMI, and 53.7% having an anamnesis. Eat_fast, Supper_time, After_supper and No_breakfast are variables regarding eating habits, and 34.4%, 42.8%, 12.1% and 23.5% answered “yes” for these variables, respectively. Exercise, Daily_activity and Walk_fast represent exercise and physical abilities, and 16.7%, 25.6% and 38.3% answered 1 for these variables. For Smoke, 38.9% were smokers. Alcohol_freq and Alcohol_amount represent alcohol consumption; 34.9%, 23.9% and 41.2% answered 0, 1 and 2 for Alcohol_freq, and 34.9%. 21.1%, 29.5%, 12.2% and 2.4% answered 0, 1, 2, 3 and 4 for Alcohol_amount, respectively. For Sleep, 61.3% answered “sleeping well”.
The result of estimation is given in Table 2. As the previous model, the estimate of First_SBP is highly significant and t-value is 52.16. The estimated value is 0.235 which is very close to that of Model 1A (0.224). This means that a similar relation holds for these variables even if the various factors of individuals are considered. The estimates of Age, BMI, Alcofol_freq and Alcohol_amount are negative significant at the 1% (Age and BMI) and 5% (Alcofol_freq and Alcohol_amount). These variables make the difference smaller. One the other hand, the estimates of Female and Daily_activity are positive and significant at the 1% level and these variables make the difference larger. Other variables were not significant at the 5% level. Figure 6 is a graph of residuals calculated from Model 1B. The distribution is almost symmetric and systematic skewness was eliminated in this model.
3.2. Difference of DBP
Figure 7 shows the relation of the first measurement and difference for DBP. Like the SBP case, there exists a positive correlation between the two variables and the correlation coefficient is 0.365. The gross relation of the first measurement is given by the model.
Table 2. Results of estimation for difference of SBP measurements (Model 1B).
SE: standard error, *: significant at the 5% level, **: significant at the 1% level.
Figure 6. Distribution of residuals in Model 1B.
Figure 7. Relation of the first measurement and difference (DBP).
Model 2A:
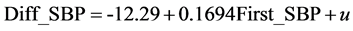 , R2 = 0.1320,
, R2 = 0.1320, 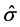 = 5.479. (4)
= 5.479. (4)
(0.2862) (0.00326)
where Diff_DBP is the difference between the first and second DBP measurements and First_DBP is the first DBP measurement. Next, we consider the following model that contains variables that may affect Diff_DBP, Model 2B:
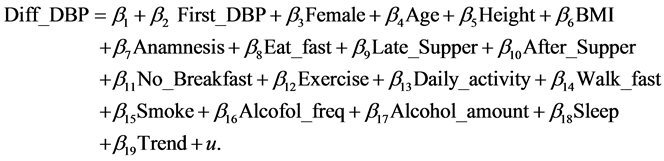 (5)
(5)
The explanatory variables other than First_DBP were the same as in the case of SBP (Model 1B). The result of estimation is given in Table 3. The estimate of First_DBP is 0.1766 and similar to the result of Model 2A and the relation between Diff_DBP and First_DBP does not change much even if we consider various characteristics of individuals. The estimates of Age, BMI, No_Breackfast, Alcohol_amount, and Sleep are negative and significant at the 1% (BMI and Alcohol_amount) and 5% (other variables). On their hand, the estimate of Female,
Table 3. Results of estimation for difference of DBP measurements (Model 2B).
SE: standard error, *: significant at the 5% level, **: significant at the 1% level.
Daily_activity are positive at the 1% level. The estimates of Age, Female, BMI and Alcohol_amount are significant for both SBP and DBP and these variables are considered as important variables affecting the BP measurements.
4. Discussion
Figure 8 is the relationship between the first measurement and mean of difference of SDP for male, age 50 and values of other variables are obtained means for non-dummy variables and medians for dummy variables using the estimated results of Model 1B. This individual is considered a typical individual in our dataset. The first measurement becomes larger than the second one if the first mea- surement is over 116.4 mmHg. When the first measurements are 140, 160 and 180 mmHg, the second measurements are, on average, 134.5, 149.8 and 165.1 mmHg; that is, the use of just one measurement may result in inflated values. We use these figures as an example because, according to the guidelines of the WHO and the International Society of Hypertension (ISH) [34] , hypertension is classified into three categories: grade 1 (middle hypertension) when SBP is 140 - 159 mmHg; grade 2 (moderate hypertension) when SBP is 160 - 179 mmHg; and grade 3 (severe hypertension) defined as SBP is 180 mmHg or over. The standard error of Model 1B is 8.6 mmHg, and a large measurement error remains even if the various characteristics of an individual and WCE are considered. This result suggests that BP is affected by mental conditions such as stress, and sometimes, fluctuates a large amount even in a short period. Hence, the BP measurement should be done carefully, considering the influence of mental condition.
The same phenomenon occurs for DBP; the second measurement is lower than the first one if the first measurement is over 66.7 mmHg. When the first DBP measurement is 90, 100 or 110 mmHg (corresponding to grade 1, 2 and 3 of the WHO/ISH DBP criteria for DBP), the second one becomes 85.9, 94.1 or 102.4 mmHg, respectively. The standard error of Model 2B is 5.4 mmHg.
These findings suggest the possibility of not only the existence of large biases (i.e. WCE) but also a large difference between the two measurements even after the characteristics of individuals are corrected for. In other words, one-time measurement may not be very much reliable, so that the results of previous studies may need to be revised [4] [5] . Measuring BP twice even in a short period
Figure 8. The mean of difference and the first measurement (SBP).
might improve problems in BP measurement: i.e., both WCE and measurement error.
In Japan, when BP is measured twice, hospitals and clinics can report the value which they think is most proper, such as an average of two measurements, as “another value” [33] ; in our dataset, 94% of reported values were averages and 6% were the minimum of the two measurements. However, the results of this study imply that neither average nor minimum values may be proper. Although it becomes smaller, the bias due to WCE remains if the mean is used. If the mini- mum is used (usually the second measurement), the basic statistical theorem suggests that the variance due to the measurement error becomes larger than the average case. Alternative methods include i) correcting the first measurement by Models 1B and 2B and ii) taking an average of the corrected first measurement and second measurement.
There is no doubt that accurate and cost-effective BP measurement is essential for determining the existence and severity of hypertension. As we described in this paper, a single measurement has a reliability problem due to WCE and mea- surement errors. However, more accurate measurements, such as 24-h AOBP, are costly and difficult to perform, especially when collecting data from many individuals. Therefore, further studies are necessary to find ways to measure BP more accurately and cost-effectively. Methods using internet technology and the development of proper devices could provide solutions to this problem.
5. Conclusions
In this paper, we evaluated the difference between the first and second measure- ments of BP when BP was measured twice, using the results of 17,775 checkups. The two consecutive measurements showed large fluctuations even though they were measured at short intervals (usually within 30 minutes) for both SBP and DBP. The first measurements were 6.7 and 2.4 mmHg higher than the second ones for SBP and DBP, and the existence of a white coat effect was strongly suggested. Then, the factors that might have affected the difference between the two measurements were analyzed by regression models. For both SBP and DBP, the differences between the first and second measurements increased as the first measurements increased. Age, gender, BMI and alcohol consumption are other important factors shown to affect the difference. In case of a typical individual (male and age 50), the WHO/IS hypertension criteria of 140/90, 160/100 and 180/110 mmHg in the first measurement corresponded to 135/86, 150/94 and 165/102 mmHg in the second measurement.
We just evaluated the checkups in which BP was measured twice, and a sample selection bias might exist. The inspection interval between two BP measurements might affect the difference. However, exact lengths of intervals were not reported. Having an accurate and cost-effective BP measurement method is essential for diagnosing and treating hypertension. For this purpose, the use of internet technology and development of proper devices may be important. These are subjects to be studied in future.
Acknowledgements
This study was approved by the Institutional Review Boards of the University of Tokyo (Number: KE16-30). The authors would like to thank the health insurance society providing us the data for their sincere cooperation. We would also like to thank an anonymous referee for his/her helpful comments and suggestions.
Cite this paper
Nawata, K. and Kimura, M. (2017) Reliability of Blood Pre- ssure Measurements: An Analysis of the White Coat Effect and Its Fluctuations. Health, 9, 506-519. https://doi.org/10.4236/health.2017.93036
References
- 1. World Health Organization (2016) Raised Blood Pressure.
http://www.who.int/gho/ncd/risk_factors/blood_pressure_prevalence_text/en/ - 2. Vasan, S.R., Larson, M.G., Leip, E.P., et al. (2001) Impact of High-Normal Blood Pressure on the Risk of Cardiovascular Disease. The New England Journal of Medicine, 345, 1291-1297.
https://doi.org/10.1056/NEJMoa003417 - 3. Prospective Studies Collaboration (2002) Age-Specific Relevance of Usual Blood Pressure to Vascular Mortality: A Meta-Analysis of Individual Data for One Million Adults in 61 Prospective Studies. The Lancet, 360, 1903-1913.
https://doi.org/10.1016/S0140-6736(02)11911-8 - 4. Chobanian, A.V., Bakris, G.L., Black, H.B., et al. (2003) Seventh Report of the Joint National Committee on Prevention, Detection, Evaluation, and Treatment of High Blood Pressure. Hypertension, 42, 1206-1252.
https://doi.org/10.1161/01.HYP.0000107251.49515.c2 - 5. National Heart, Lung, and Blood Institute, U.S. Department of Health and Human Services (2004) National High Blood Pressure Education Program. Seventh Report of the Joint National Committee on Prevention, Detection, Evaluation, and Treatment of High Blood Pressure (Complete Report).
https://www.nhlbi.nih.gov/files/docs/guidelines/jnc7full.pdf - 6. Mancia, G., Fagard, R., Narkiewicz, K., et al. (2013) 2013 ESH/ESC Guidelines for the Management of Arterial Hypertension: The Task Force for the Management of Arterial Hypertension: European Society of Cardiology (ESC). Journal of Hypertension, 31, 1281-1357.
https://doi.org/10.1097/01.hjh.0000431740.32696.cc - 7. AACN Practice Alert (2016) Obtaining Accurate Noninvasive Blood Pressure Measurements in Adults. Critical Care Nurse, 36, e12-e16.
https://doi.org/10.4037/ccn2016590 - 8. Omiboni, S., Aristizabal, D., De la Sierra, A., et al. (2016) Hypertension Types Defined by Clinic and Ambulatory Blood Pressure in 14143 Patients Referred to Hypertension Clinics Worldwide. Data from ARTEMIS Study. Journal of Hypertension, 34, 2187-2198.
https://doi.org/10.1097/HJH.0000000000001074 - 9. Almeida, J., Monteiro, J., Silva, J.A., Bertoquini, S. and Polónia, J. (2016) Central Pressures and Central Hemodynamic Values in White Coat Hypertensives Are Closer to Those of Normotensives than to Those of Controlled Hypertensives for Similar Age, Gender, and 24-h and Nocturnal Blood Pressures. Revista Portuguesa de Cardiologia (Portuguese Journal of Cardiology), 35, 559-567.
https://doi.org/10.1016/j.repc.2016.05.006 - 10. Bastos, J.M. (2016) Pulse Wave Velocity, Central Aortic Pressure, and Arterial Reflection Waves in White Coat Hypertension. Revista Portuguesa de Cardiologia (Portuguese Journal of Cardiology), 35, 569-571.
- 11. Cheng, H.-M., Pearson, A., Sung, S.-H., Yu, W.-C., Chen, C.-H. and Karnon, J. (2015) Cost-Effectiveness of Non-Invasive Central Blood Pressure Monitoring in the Diagnosis of Hypertension. American Journal of Hypertension, 28, 604-614.
https://doi.org/10.1093/ajh/hpu214 - 12. Boggia, J., Lee, Y., Hansen, L., et al. (2007) Prognostic Accuracy of Day versus Night Ambulatory Blood Pressure: A Cohort Study. The Lancet, 370, 1219-1229.
https://doi.org/10.1016/S0140-6736(07)61538-4 - 13. Conen, D. and Bamberg, F. (2008) Noninvasive 24-h Ambulatory Blood Pressure and Cardiovascular Disease: A Systematic Review and Meta-Analysis. Journal of Hypertensions, 26, 1290-1299.
https://doi.org/10.1097/HJH.0b013e3282f97854 - 14. Fagard, R.H., Celis, H., Thijs, L., et al. (2008) Daytime and Night Time Blood Pressure as Predictors of Death and of Death and Cause-Specific Cardiovascular Events in Hypertension. Hypertension, 51, 55-61.
https://doi.org/10.1161/HYPERTENSIONAHA.107.100727 - 15. Wohlfahrt, P., Cifková, R., Movsisyan, N., et al. (2016) Threshold for Diagnosing Hypertension by Automated Office Blood Pressure Using Random Population. Journal of Hypertension, 34, 2180-2186.
https://doi.org/10.1097/HJH.0000000000001076 - 16. Arrieta, A., Woods, J.R., Qiao, N. and Jay, S.J. (2014) Cost-Benefit Analysis of Home Blood Pressure Monitoring in Hypertension Diagnosis and Treatment. Hypertension, 64, 891-896.
https://doi.org/10.1161/HYPERTENSIONAHA.114.03780 - 17. Moran, A.E., Odden, M.C., Thanataveerat, A., et al. (2015) Cost-Effectiveness of Hypertension Therapy According to 2014 Guidelines. The New England Journal of Medicine, 375, 447-455.
https://doi.org/10.1056/NEJMsa1406751 - 18. Gadilhac, D.A. and Kim, J. (2015) Potential Cost-Saving May Be Considerable with Management of Hypertension According to Updated US Hypertension Guidelines, But for Women Aged 35 - 44 Years These Benefits Are Unlikely. Evidence-Based Medicine, 20, 150.
https://doi.org/10.1136/ebmed-2015-110202 - 19. Cuspidi, C., Sala, C., Grassi, G. and Mancia, G. (2016) White Coat Hypertension: To Treat or Not to Treat? Current Hypertension Reports, 18, 80.
https://doi.org/10.1007/s11906-016-0687-9 - 20. Cavallini, M.C., Roaman, M.J., Pekering, T.G., Schwartz, J.E., Pini, R. and Devereux, R.B. (1995) Is White Coat Hypertension Associated with Arterial Disease or Left Ventricular Hypertension? Hypertension, 26, 413-419.
- 21. Cuspidi, C., Marabini, M., Lanaoti, L., et al. (1995) Cardiac and Carotid Structure in Patients with Established Hypertension and White-Coat Hypertension. Journal of Hypertensions, 13, 1707-1711.
https://doi.org/10.1097/00004872-199512010-00036 - 22. Predomenico, S.D., Lapenna, D., Gulielmi, M.D., et al. (1995) Target Organ Status and Serum Lipids in Patients with White Coat Hypertension. Hypertension, 26, 801-807.
https://doi.org/10.1161/01.HYP.26.5.801 - 23. Verdecchia, P., Schulma, P., Borginoi, C., Ciucci, A. and Porcellati, C. (1997) Prognostic Significance of the White Coat Effect. Hypertension, 29, 1218-1224.
https://doi.org/10.1161/01.HYP.29.6.1218 - 24. Ribeiro, L., Gama, G., Santos, A., et al. (2000) Arterial Distensibility in Subjects with White-Coat Hypertension with and without Diabetes or Dyslipodaemia: Comparison with Normotensives and Sustained Hypertensives. Blood Pressure Monitoring, 5, 11-17.
https://doi.org/10.1097/00126097-200002000-00003 - 25. Kario, K., Shimada, K., Schwartz, J.E., Matsuo, T., Hoshide, S. and Pickering, T.G. (2001) Silent and Clinically Overt Stroke in Older Japanese Subjects with White-Coat and Sustained Hypertension. Journal of the American College of Cardiology, 38, 238-245.
- 26. Gustavsen, P.H., Hoegholm, A., Bang, L.E. and Kristensen, K.S. (2003) White Coast Hypertension Is a Cardiovascular Risk Factor: A 10-Years Follow-Up Study. Journal of Human Hypertension, 17, 811-817.
https://doi.org/10.1038/sj.jhh.1001643 - 27. Verdecchis, P., Reboldi, G.P., Angeli, F., et al. (2005) Short- and Long-Term Incidence of Stroke in White-Coat Hypertension. Hypertension, 45, 203-208.
https://doi.org/10.1161/01.HYP.0000151623.49780.89 - 28. Franklin, S.S., Thijs, L., Asayama, K., et al. (2016) The Cardiovascular Risk of White-Coat Hypertension. Journal of the American College of Cardiology, 68, 2033-2043.
https://doi.org/10.1016/j.jacc.2016.08.035 - 29. Muncia, G. and Grassi, G. (2016) The Heterogeneous Nature of White-Coast Hy- pertension. Journal of the American College of Cardiology, 68, 2044-2046.
https://doi.org/10.1016/j.jacc.2016.08.043 - 30. Marios, E., Michas, F., Stamatelopoulas, K., et al. (2016) White-Coat Systolic Hypertension Is a Risk Factor for Carotid Atherosclerosis. Journal of Clinical Hypertension, 18, 1095-1102.
https://doi.org/10.1111/jch.12888 - 31. Japanese Law Translation (2009) Industrial Safety and Health Act.
http://www.japaneselawtranslation.go.jp/law/detail/?id=1926&vm=&re= - 32. Nawata, K., Matsumoto, A., Kajihara, R. and Kimura, M. (2017) Evaluation of the Distribution of and Factors Affecting Blood Pressure Using Medical Checkup Data in Japan. Health, 9, 124-137.
https://doi.org/10.4236/health.2017.91009 - 33. Ministry of Health, Labour and Welfare (2008) Tokutei kennshin/hoken shidou no houkoku youshiki ni kansuru kitei tou [Rules and Related Guide Lines of Report for Specific Health Checkups and Specific Health Guidance]. (In Japanese).
http://www.mhlw.go.jp/stf/shingi/2r9852000001wy6m-att/2r9852000001wyun.pdf - 34. Guidelines Subcommittee (1990) 1999 World Health Organization—International Society of Hypertension Guidelines for Management of Hypertension. Journal of Hypertension, 17, 151-183.










