Received 19 May 2016; accepted 26 June 2016; published 29 June 2016

ABSTRACT

A hydraulic jump is a rapid transition from supercritical flow to subcritical flow characterized by the development of large scale turbulence, surface waves, spray, energy dissipation and considerable air entrainment. Hydraulic jumps can be found in waterways such as spillways connected to hydropower plants and are an effective way to eliminate problems caused by high velocity flow, e.g. erosion. Due to the importance of the hydropower sector as a major contributor to the Swedish electricity production, the present study focuses on Smoothed Particle Hydrodynamic (SPH) modelling of 2D hydraulic jumps in horizontal open channels. Four cases with different spatial resolution of the SPH particles were investigated by comparing the conjugate depth in the subcritical section with theoretical results. These showed generally good agreement with theory. The coarsest case was run for a longer time and a quasi-stationary state was achieved, which facilitated an extended study of additional variables. The mean vertical velocity distribution in the horizontal direction compared favorably with experiments and the maximum velocity for the SPH- simulations indicated a too rapid decrease in the horizontal direction and poor agreement to experiments was obtained. Furthermore, the mean and the standard deviation of the free surface fluctuation showed generally good agreement with experimental results even though some discrepancies were found regarding the peak in the maximum standard deviation. The free surface fluctuation frequencies were over predicted and the model could not capture the decay of the fluctuations in the horizontal direction.

Keywords:

SPH, Hydraulic Jump, Conjugate Depth, Free Surface Fluctuation, Vertical Velocity Distribution

1. Introduction

Fluid mechanics of large hydropower plants are characterized by very high flow rates and large physical dimensions both in production and spill waterways. The hydraulic head harvested in production needs to be handled when spillways are engaged. In open spillways, this is done by accelerating the flow and then using the dissipative features of a hydraulic jump. Hydraulic jumps are an effective way to eliminate problems caused by high velocity flow, e.g. erosion. The lower velocities past the jump may also create beneficial flow conditions for migrating species such as salmonoids [1] . A hydraulic jump is a rapid transition from high velocity supercritical flow to low velocity subcritical flow with rise of the free surface to keep continuity. The jump is characterized by the development of large scale turbulence, surface waves, spray, energy dissipation and considerable air entrainment. The highly turbulent transition zone is usually referred to as the roller and the start of the roller, the jump toe or the impingement point. A hydraulic jump is typically characterized by its inflow Froude number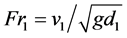, where 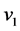is the depth average upstream flow velocity; 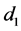is the upstream depth and g is the acceleration of gravity, see Figure 1. Based on the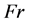, the jump may be classified into five types: undular, weak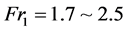, oscillating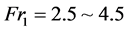, steady 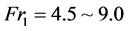and strong 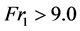, each with its own distinct characteristics [2] . By applying the continuity and momentum equation in integral form, a dimensionless relationship of the upstream depth 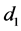and downstream depth 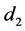can be obtained. For a horizontal and rectangular channel this procedure yields the Bélanger equation [2] ,

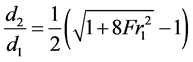. (1)

Hager, Bremen and Kawagoshi [3] reviewed a broad range of data and correlations and proposed a semi-em- pirical relationship for the length of the roller as,

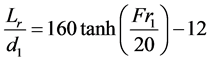, (2)

in the range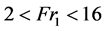. The external geometry of hydraulic jumps has been studied for a long time and only recently, the internal flow structures have been considered. Depending on the type of jump, a number of regions in the roller can be identified [4] and [5] , see Figure 1. For steady jumps, a boundary layer is seen close to the bottom which transitions in the vertical direction are into a high velocity jet or core region. Continuing in the vertical direction from the bottom, a highly turbulent air-water shear layer is observed where bubble breakup and coalescences occur and momentum is transferred to the region above. The final region is a highly aerated recirculation region with significant free surface wave and splash production.

Several authors have investigated the velocity field in the abovementioned regions using different experimental techniques, e.g. [4] - [8] . Chanson [9] showed that the velocity profiles in the developing shear layer followed a wall jet pattern proposed earlier by [4] and [6] . The maximum velocity in the horizontal direction had a longitudinal decay with increasing distance from the jump toe and the following the empirical function,

, (3)

where x is the distance downstream of the inlet and is the location of the jump toe, revealed the best correlation based on the data of [4] [9] - [11] . Long, Rajaratnam, Steffler and Smy [12] investigated hydraulic jumps with inflow using a high speed video camera in a horizontal rectangular channel. It was postulated in [12] that at any given time when the roller is at its most upstream location, the maximum number of vortices exists and their size increase in the downstream direction. The vortices showed an anticlockwise rotational tendency and vortex-pairing of smaller vortex structures was observed. Eventually, the smaller vortices merged with a semi-stationary larger vortex at the end of the roller causing a forward spill of water enabling further vortex production at the impingement point. At this stage, the jump toe was at the most downstream location observed and [12] argued that the vortex production was linked with the jump toe fluctuations. Mossa [13] investigated the oscillating behavior of several different hydraulic jumps using point gauge and concluded that a correlation between jump toe fluctuations and vortex structures in the roller is evident. Besides affecting the jump toe, the vortex structures influence the free surface. Mouazé, Murzyn, and Chaplin [14] investigated the behavior of the free surfaces using resistivity probes for four different hydraulic jumps with partially developed inflow conditions. At the jump toe, where bubbles were generated and entrained, there was a slight increase in the free surface elevation while a sudden large gradient in fluctuation was seen. Downstream the jump toe, a maximum in free surface fluctuations was observed indicating strong turbulence. Mouazé, Murzyn, and Chaplin [14] argued that the fluctuations were caused by large coherent structures reaching the free surface generated in the shear and roller regions, generally characterized by large recirculation vortices and bubbles. Further downstream, a large dissipative zone emerged as fluctuations decreased significantly and the free surface became almost horizontal. Murzyn, Mouazé, and Chaplin [15] continued the work of [14] but with a different experimental technique (wire gauges) and came to a similar conclusion. Kucukali and Chanson [10] investigated free surface fluctuations in hydraulic jumps with slightly larger inflow Froude number than previous studies using ultrasonic displacement meters, seeing the extended report [16] . Yet again, data of the mean free surface elevation showed a gradual increase towards the theoretical value in the downstream direction and the peak in standard deviation was typically found at. Murzyn and Chanson [17] (see extended report [18] ) used the same set-up and measuring apparatus as [10] and showed that the maximum standard deviation of free surface fluctuations was best correlated by the function

, (4)

where is the standard deviation of free surface fluctuations. Fast Fourier Transform (FFT) analysis of the displacement meter output signal indicated dominant frequencies in the range of 1 - 4 Hz anda minor tendency of the frequency to decrease in the downstream direction was noted. Murzyn and Chanson [17] showed also that the dimensionless Strouhal number, where is the frequency, decreased rapidly with increasing Reynolds number. More recently, Chachereau and Chanson [19] (see extended report [20] ) investigated hydraulic jumps with relatively small and large with acoustic displacement meters as the previously two studies. Similar conclusions were made as for the above studies regarding the mean and standard deviation of the free surface elevation as well as the free surface fluctuation frequencies. However, the for the free surface showed a minor decrease with increasing and data was best correlated by

, (5)

in the range.

Modelling of highly disturbed aerated free surface flows such as hydraulic jumps, is complex when grid based method is used [21] . Severe problems with mesh entanglement and determination of the free surface have been encountered [22] . The meshfree, Lagrangian particle based method Smooth Particle Hydrodynamic (SPH) has shown to be a good alternative to grid based methods to overcome such problems [23] and [24] . The technique was first proposed independently by Lucy [25] and Gingold and Monaghan [26] in the late seventies to solve astrophysical problems in three-dimensional open spaces. Today, the SPH method has been applied to a number of fields and problems [24] and the maturity of the method has increased significantly. A major advantage of SPH is that the method is meshfree, thus considerable time is saved as compared to methods that need a predefined mesh. However, as the SPH is relatively unexplored as compared to traditional finite volume methods (FVM) or finite element method (FEM) methods there are some areas that still need considerable attention. For instance, wall boundary conditions are generally difficult to set in SPH as they do not appear in a natural way within the SPH formalism. Furthermore, the SPH method is typically slower computational wise since the time step depends on the speed of sound and the explicit integration techniques used.

A few papers have been devoted to SPH modelling of hydraulic jumps. López, Marivela and Garrote [27] investigated the capability of the SPH method to reproduce mobile hydraulic jumps with different inflow. The 2D geometrical set-up composed of a tank and a gate, through which water discharged into a stilling basin where a weir triggered the jumps. Good agreement with experimental and theoretical results was shown for less than five. Jonsson, Jonsén, Andreasson, Lundström and Hellström [28] investigated the effects of altering the spatial resolution of the SPH particles and its impact on hydraulic jump behavior. Good agreement for the conjugate depth when comparing with the theoretical value was obtained for all cases. Federico, Marrone, Colagrossi, Aristodemo and Antuono [29] developed a 2D SPH model to enforce inlet and outlet boundary conditions and demonstrated through three cases, one being a hydraulic jump test case, the general ability of the SPH method to handle uniform, non-uniform and unsteady flows. By implementing inlet and outlet boundary conditions, the use of a tank and gate as well as a weir was no longer necessary hence improving the efficiency of the computation. Several jumps with different were investigated and good agreement when compared with theoretical values was found for the conjugate depth. Furthermore, good agreement was obtained for the internal velocity field when compared with the experimental work by [7] although the size of the vortex structures was generally over predicted. Chern and Syamsuri [30] displayed the possibility to investigate the effects of a corrugated bed on the hydraulic jump characteristics using SPH. The geometrical setup was similar to the one used by [27] but a more sophisticated method to model turbulence was employed, namely the laminar and sub-particle scale (SPS) technique. Several corrugated bed types were investigated and evaluated using the conjugate depthratio, jump length, bottom shear stress distribution and the energy dissipation. Padova, Mossa, Sibilla and Torti [31] investigated 3D undular hydraulic jumps influenced by waves generated at the channel walls. The results showed a reasonable agreement in terms of time-average water depths and longitudinal velocity components. However, poor agreement was found for the prediction of the inclination of the oblique wave front and [31] argued that this is possibly an effect of the wall boundary conditions used.

Present study will focus on the general behavior of hydraulic jumps when using the meshless, Lagrangian particle method SPH. Special attention will be given on how the spatial resolution of the SPH particles impacts the overall behavior of the jump and the conjugate depth. Apart from the geometrical parameters such as depth, the internal velocity field and its impact on the free surface will be studied. Based on the averaged velocity field the jump length will be determined and compared to experiments. The instantaneous velocity field showed large coherent vortices which affected the free surface. The fluctuations of the free surface will be studied extensively and numerical results will be compared to experimental data, e.g. the standard deviation and fluctuations frequencies.

2. Method

2.1. Governing Equations

In the SPH-method, the fluid domain is represented by a set of non-connected particles which possess individual material properties, e.g. density, velocity and pressure [32] . Besides representing the problem domain and acting as information carriers the particles also act as the computational frame for the field function approximations. As the particles move with the fluid their material properties changes as a function of time and spatial co-ordinate due to interactions with neighboring particles. In the following text, the superscripts and are used to denote coordinate directions and the subscripts i and j denotes particle indices. The continuity and momentum equations can be written in the SPH formalism according to,

, (6)

, (7)

where is the density, m is the particle mass; is the acceleration due to gravity and and is the position and the velocity vector respectively [32] . The term in Equation (6) and (7) is the gradient of the kernel function [33] , i.e.

, (8)

where the kernel function is

. (9)

In both Equation (8) and (9), h is the smoothing length; is the normalized distance between two particles; is the number of space dimensions and is the derivative of

(10)

where is a constant of normalization defined for one-, two- and three dimensional spaces as;, and [32] . By choosing according to Equation (10) the commonly used cubic B-spline kernel is obtained [32] . The total stress tensor in Equation (7) is made up from two parts [32] , the isotropic pressure p and the deviatoric viscous stress according to

. (11)

The NULL material model implemented in software package LS-DYNA defines the deviatoric viscous stress as,

. (12)

where is the deviatoric strain rate [33] . By setting the dynamics viscosity to zero the total stress tensor reduces to, where p is defined by an equation-of-state (EOS). The EOS relates density variation to pressure as

, (13)

where is the adiabatic speed of sound and is the initial density [32] . By using the Linear

Polynomial EOS implemented in LS-DYNA [33] as,

, (14)

where and setting and the other constants to zero Equation (13) is obtained. The artificial viscosity proposed by [34] is implemented as,

, (15)

where

, (16)

and are constants; is the distance vector and and are the mean speed of sound and density, respectively. If the smoothing length h is dynamic. The term is used to avoid the denominator to go to zero. In literature, many authors suggest setting in the range 0.01 - 0.1 and [35] and [36] . Following [37] , the artificial viscosity constants are set to and. With the reduction of the total stress tensor, the inclusion of the artificial viscosity term together with the symmetric properties of the term, the momentum equation reduces to the familiar expression [32] ,

. (17)

A first order time integration scheme is used and the time step is determined according to,

, (18)

where is the Courantcoefficient usually set equal to unity [33] .

2.2. Boundary Conditions

Wall boundaries were modelled as rigid shell finite elements and the coupling between the boundaries and the SPH-particles were governed by a penalty based “node-to-surface” contact-algorithm [33] [37] [38] . This is a so-called one-way contact where the SPH particles are defined as the slave side and the FEM elements as master side. In applying the penalty method, the slave nodes were checked for penetration through the master surface. If a slave node penetrated, an interface spring was placed between the master surface and the node. The spring stiffness was chosen approximately in the order of magnitude as the stiffness of the interface element normal to the interface. The resultant force applied to the SPH particle in the normal direction of the FEM element was proportional to the amount of penetration. As the normal component was considered only the wall boundaries are frictionless. This approach can be compared with the Lennard-Jones-type boundary condition where a central force is applied to fluid particles [36] .

2.3. Geometrical and Numerical Setup

A two dimensional horizontal spillway channel and hydraulic jump were investigated in present work with a single phase (water) model. The schematic geometrical setup is shown in Figure 2. Inside the computational box (dashed lines), SPH particles were activated meaning that the governing equations were solved. Outside the

box, SPH particles maintained the state from previous active time step or an externally imposed state and hence no governing equations were solved. By placing a fixed number of SPH particles in an ordered configurationoutside the computational box an inlet was obtained, see the black box at the inlet section in Figure 2. The SPH particles entering the domain had a prescribed inlet velocity of and a depth of generating a hydraulic jump with Froude number. The number of particles predefined outside the domain was matched with the total simulation time, i.e. 5 s or 30 s see Table 1. Above the inlet, a gate was placed to stop SPH particles from exiting the domain in the upstream direction. The stilling basin, located between the inlet and the weir, measured 1.1 m and was prefilled to the same depth as the incoming particles in order to trigger the jump faster. The weir height was set to and measured 0.8 m in the downstream direction. At the end of the weir, the boundary of the computational domain was used as an outlet where the state of the SPH particles was “frozen” in time except for their position. The dimensions of the computational box was and. All SPH particles were initially placed on a structured grid and the initial density. Usually, is reduced to 10 times the maximum flow velocity [36] . However, initial results showed severe compressible effects and contact instabilities, hence was set equal to the adiabatic speed of sound of. In order to investigate the influence of altering the number of nodes representing the system, four cases with different spatial resolution was set up. Here, the characteristic length scale was chosen to the incoming jet depth and consequently, the SPH spatial resolution of the four cases were, , and. The rigid shell finite elements, representing wall boundaries, measured half the initial SPH spatial resolution and varied for each case. A static smoothing length of 1.2 times the initial interpartical spacing was used for all cases, see [37] . All cases was run for 5 s, except the coarsest which was run for 30 s, and data was saved at each 0.01 s, see Table 1. All simulations were conducted using LSTC LS-DYNA v. 971 R7.0.0 on multicore Linux workstations. The post processing method proposed by [37] was used to visualize and interpolate the SPH data. Statistical measurements of the deviations of conjugate depth was determined by the following formulas,

, (19)

, (20)

A perfect agreement of numerical and theoretical results implies that and [39] .

3. Result and Discussion

In Figure 3 and Figure 4, the absolute velocity field for the coarsest and the finest case is shown. As an expected result, the number of detectable flow features increased with resolution, compare Figure 3 and Figure 4. All cases showed a similar overall behavior which can be described as follows. During the initial time steps, the stationary fluid in the stilling basin resisted the fast incoming jet thus creating a “mushroomlike” wave similar to the wave created in dam break flows over a wet bed (see [40] and [41] ). The wave broke in both up- and down-stream directions and formed a moving hydraulic jump. The jump propagated in the downstream

direction until it reached the weir, see Figure 3 & Figure 4 at 2 s. During this phase a minor difference the position of the jump toe was seen among the cases. At the weir, a bulking effect with linear increase of the free surface was observed and the jump toe shifted propagation direction, compare Figure 3, Figure 4 and Figure 5. As the jump shifted to an upstream propagation direction the difference of the position of the jump toe increased. The more refined cases showed a lower upstream propagation rate compared to the less refined. It was assumed, however, that the propagation rate was not zero and thus the more refined cases would have reached the gate if the simulation time was increased. The coarsest case which was set up to run until 30 s, continued to propagate upstream until approximately 11 s when it reached the gate and the inlet. Past 11 s, a quasi-stationary state was obtained. Generally, for experimental studies (e.g. [10] and [17] ) the jump toe becomes quasi-stationary at a certain distance downstream the inlet after an initial transient phase and not at the inlet itself. The continuing propagation of the jump toe in the upstream direction shown for the numerical results could potentially be explained by the frictionless contact algorithm used in the model. In all cases, especially the coarser ones, an “artificial” boundary layer close to the bottom affected the jet behavior, see Figure 3 at 1 s and Figure 6. However, this

should not be interpreted as an actual boundary layer. It was more likely an effect of the truncated kernel domain due to the lack of SPH nodes outside the boundary. Considerable research has been devoted to this topic and a possible solution is the use of a different boundary condition such as the ghost particle [42] , the repulsive particle [36] or the dynamic particle method [43] . Furthermore, the various density filters and kernel and kernel gradient correction methods proposed in literature (e.g. [44] ) may also be applied to reduce these unwanted effects.

In Figure 5, the dimensionless conjugate depth as a function of time is shown. The position where the depth was sampled was chosen to not include the effects by the weir as the flow depth was reduced to meet continuity, see for instance Figure 4. Good agreement was obtained for the conjugate depth which was comparable to the results of [27] - [29] . At roughly 0.8 s, increased rapidly followed by the almost linear increase, see Figure 5(a). The maximum depth was also visible followed by the release of water in the upstream direction. Beyond 2.5 s, an oscillatory behavior of the numerical depth for all cases around the theoretical value, determined by Equation (1), was observed. In Figure 5(b), the dimensionless conjugate depth for the coarsest case is shown only. As mentioned above, the jump toe reached the gate and the inlet at approximately 11 s which was indicated by a slight increase of the depth. Statistical measures, A and P, of the behavior of the dimensionless conjugate depth for the four cases were obtained by applying Equation (19) and Equation (20), see Table 2.

To exclude the initial transient phase, data was collected in the time interval 2.5 s to 5.0 s for all cases and in the interval 15 s to 30 s for the coarsest case. Generally, coarser cases showed better agreement than finer cases. This behavior could be explained by the increased number of flow features resolved which as reported in [28] and [37] . Henceforth, data from the coarsest case in the time interval 15 s to 30 s (the quasi-stationary state) will be discussed. In Figure 6, the dimensionless time averaged vertical velocity distribution in the downstream direction is shown where black lines represents data each 0.025 m in the interval. The incoming jet together with the recirculation zone represented by the negative values for the first steps in the downstream direction is visible. These results compared favorably with experimental results, see for instance [5] and [9] . Further downstream, the jet weakened and the velocity profile became almost uniform. However, two significant discrepancies were seen. Firstly, the effects of the “boundary layer” discussed above were seen close to the bottom. This was assumed to be an effect of the truncated kernel and not an actual boundary layer. Secondly, the velocity profiles collapsed to zero velocity close to the free surface. This was an effect of the interpolation and averaging process as interpolation points outside the water were given a value of zero. The red line in Figure 6 represent the first position downstream the jump toe with non-negative averaged velocity in the downstream direction. Hence, this position can interpreted as the end of the roller section and the length of the jump. Comparing the numerical value of the jump length with theoretical value by using Equation (2) a −25% discrepancy was obtained. The blue star markers in Figure 6 represent the averaged maximum velocity in the downstream direction which was compared with the empirical function (Equation (3)) obtained by [9] , see Figure 7. The jump toe position for the SPH results was assumed to be zero, i.e.. As can be seen in Figure 7, decreased rapidly downstream indicating a too dissipative zone as compared with the empirical function. A lower value of the artificial viscosity constant or a more sophisticated viscosity model could potentially improve this behavior. Beyond, stabilized and a more uniform velocity field was achieved. A minor tendency of to increase was also observed which can be explained by the influence of the weir, as discussed above.

As mentioned in the introductory section, several authors have commented on the existence and the implication of large vortex structures and its effect on the free surface in the roller region. The vortex paring mechanism and the merging with the stationary vortex reported in [12] were not observed in present results. However, individual

vortices translated with increasing size in the downstream direction in agreement with [12] . Figure 8 presents a snapshot of the flow structures found for the coarsest case where the blue lines represents streamlines. An active vortex is seen close to the jump toe which was translating downstream as well as a decaying vortex further downstream. The effects on the free surface of the vortices are marked in red and green. In Figure 9, the dimensionless averaged free surface profile is shown and good agreement between numerical and experimental results were observed, [16] [18] [20] . A minor over prediction of the averaged free surface profile was however noted which could be coupled to the jump toe reaching the inlet and the gate, hence, increasing the depth as discussed above, compare Figure 5(b) and Figure 9. Figure 10 presents the dimensionless standard deviation of the free surface fluctuations which indicated a minor under prediction as compared to the experimental results. Also, the peak was shifted in the downstream direction. A plausible explanation is that a single phase model was used where the dissipative contribution from the air bubbles and turbulence was not accurately included and thus vortex breakup and diffusion occurred further downstream.

However, when investigating the dimensionless maximum standard deviation as function of Froude number a good agreement with experimental results and the empirical function Equation (4) was observed, see Figure 11.

A Fast Fourier Transform (FFT) analysis of the numerical depth at several positions downstream the jump toe was conducted. Figure 12 presents a typical output which can be compared with outcomes from similar analysis of experimental data, see for instance [20] . The spectral analysis showed dominant frequencies in the range 2 - 5 Hz and a significant peak at approximately 3.5 Hz which was in agreement with experimental observations, see [16] [18] [20] . Figure 13 presents the characteristic free surface fluctuation frequency as function of the

dimensionless distance downstream the jump toe. In the experiments, the FFT analysis indicated several characteristic frequencies which here are shown as both individual dots and lines. For the numerical results, the characteristic frequency is shown only. Two trends are observed in Figure 13. Firstly, the numerical result over predicted the significant frequency. It should be noted, that the intensity or amplitude was greatly reduced in the horizontal direction for the FFT outcome but the most significant frequency was still at approximately 3.5 Hz. Secondly, the general trend of decreasing frequency in the downstream direction observed for the experimental data was not captured by the SPH model. Yetagain, the single phase model could be a plausible explanation to this behavior causing elevated vortex generation rates and as a consequence too high free surface fluctuation frequencies. Figure 14 presents the dimensionless Strouhal number as function of the inflow Froude number. A minor under prediction of was observed when comparing with the empirical function Equation (5) proposed by [20] , however, numerical results were within the experimental range.

4. Conclusion

Two dimensional hydraulic jumps have been investigated in present work using the Meshfree, Lagrangian particle based method Smoothed Particle Hydrodynamics. Four cases with different spatial resolution of the SPH

particles were set up and as a general result more flow features were observed for the highly resolved cases. All cases showed a tendency to propagate in the upstream direction, which was assumed to be a consequence of the frictionless boundary condition used. Furthermore, a “artificial” boundary layer was observed close to the bottom which affected the incoming jet and was likely caused by the truncated kernel due to the lack of SPH nodes outside the boundary. The conjugate depth was compared with the theoretical value for the various spatial resolutions and good agreement was achieved. For the coarsest case, which was run for 30 s, additional features were investigated as a quasi-stationary state was reached past 11 s. The vertical velocity distribution compared

fairly good with experimental results even though the length of the jump was under predicted by roughly 25%. The maximum velocity in horizontal direction indicated a too dissipative zone past the roller which was likely caused by the viscosity model used. The investigation of vortex structures and its effect on the free surface showed generally good agreement for the mean and the standard deviation, even though the peak in the standard deviation occurred further downstream as compared to the experimental results. However, when comparing the maximum standard deviation as function of the Froude number a favorable result was obtained. The investigation of free surface fluctuation frequencies indicated a general over prediction of frequencies and that the longitudinal decay was not captured by the SPH model. Also, a minor under estimation of the Strouhal number was obtained even though the outcome was within the range of experiments. This work has shown that it is possible to investigate the dynamics of the internal velocity field and its impact on the free surface in a hydraulic jump using a relative simple and coarse SPH model. However, a future study focusing on highly refined cases and a more sophisticated viscosity model would be interesting.

Acknowledgements

The research presented was carried out as a part of “Swedish Hydropower Centre-SVC”. SVC has been established by the Swedish Energy Agency, Elforsk and Svenska Kraftnät together with Luleå University of Technology, KTH Royal Institute of Technology, Chalmers University of Technology and Uppsala University www.svc.nu.

Cite this paper

Patrick Jonsson,Pär Jonsén,Patrik Andreasson,T. Staffan Lundström,J. Gunnar I. Hellström, (2016) Smoothed Particle Hydrodynamic Modelling of Hydraulic Jumps: Bulk Parameters and Free Surface Fluctuations. Engineering,08,386-402. doi: 10.4236/eng.2016.86036

References