Engineering
Vol.07 No.07(2015), Article ID:58139,6 pages
10.4236/eng.2015.77041
A New Method for the Dynamic Reserves of Gas Condensate Reservoir Using Cyclic Gas Injection Based on the Effects of Reinjection Ratio and Water Influx
Yu Xiong1, Ling Wang1, Zhongqian Zhu2, Wei Xie2
1Southwest Petroleum University, Chengdu, China
2Tarim Oilfield Research Institute, Beijing, China
Email: swpuwl@163.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 23 June 2015; accepted 18 July 2015; published 21 July 2015
ABSTRACT
As we all know, cyclic gas injection is one of the most effective development methods to improve condensate oil recovery. When dealing with the calculation of the reserves, the injection-produc- tion differences and water influx create great influence on the accuracy. Based on the existing research, we proposed a new material balance equation which considered the differences of composition between produced and injected fluids and the effect of water influx, and a solution was provided in this paper. The results of the method are closer to the actual situation because they are built on the law of conservation of mass, and the using of curve fitting method can not only avoid the use of water influx coefficient but also obtain the water influx rate and reserves at the same time. The YH-23 gas condensate reservoir is taking as a typical subject to do the research, which has been exploited by cycle gas injection for 14 years. Three different methods are used to calculate the reserves, and the results show that the method proposed in this paper has minimum error of 2.96%.
Keywords:
Condensate Gas Reservoir, Cyclic Gas Injection, Dynamic Reserves, Material Balance Method, Reinjection Ratio, Water Influx

1. Introduction
Classical material balance method is one of the fundamental tools of reservoir engineering. It can be used to determine original gas-in-place and recoverable reserves [1] - [3] . Condensate gas reservoir has special retrograde condensation phenomenon, when its formation pressure drops to below the dew-point pressure, condensate oil which is originally gas will become liquid. Depletion development will lead to a serious loss of condensate; cyclic gas injection is one of the major measures to keep formation pressure and improve condensate oil recovery [4] - [7] .
Gas cycling is a way that dry gas is separated from the produced well fluids and then injected to keep the pressure. The injected gas contains only light components, but produced well flow contains both light and heavy components. Although produced and injected fluids are both hydrocarbon fluids, there is a huge differentia in composition. When using material balance equation to determine the original gas-in-place of gas condensate reservoirs, the expression of two fluids must be separated, and otherwise the result is unreliable [8] .
In gas condensate reservoirs with edge-bottom water, water influx is one of the key parameters for determination of development scale and production plan [9] . How to calculate the rate of water invasion correctly while analyzing the performance and calculating the dynamic reserve with material balance equation is still a difficulty for a long time.
In this paper, we build a new method and solution, which can be used to determine reserves and water influx rate. The method is applicable to condensate gas reservoir developed by cyclic gas injection, which reflects the influence of water invasion and injection-production differences.
2. Derivation of Material Balance Equation
2.1. Fundamental Equation
According to the law of conversation of mass, the underground reserves can be determined by subtracting the produced oil and gas from the amounts of original reserves and dry gas injection combined, molar number is used to describe the relationship because it can’t be influenced by temperature and pressure, the equation can be expressed as Equation (1).
 (1)
(1)
where, ni is the mole number of initial reserves; nj is the mole number of underground remaining reserves; nij is the mole number of cumulative injected gas; np is the mole number of cumulative production.
The equation of authentic gas is  [10] . Using different parameters to describe the number of moles of hydrocarbons at the initial state:
[10] . Using different parameters to describe the number of moles of hydrocarbons at the initial state:
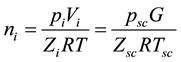 (2)
(2)
where, pi, Zi, Vi are the formation pressure, deviation factor and pore volume under the original condition respectively, psc, Zsc, Tsc are the pressure, deviation factor and absolute temperature under the standard condition respectively, G is the original condensate gas geological reserves, R is universal gas constant, T is the absolute temperature of reservoir.
Two phases, gas and liquid, exist in the formation when the bottom-hole pressure is lower than dew-point pressure, yet the two-phase deviation factor will be adopted to take place of single-phase deviation factor. The molar volume of underground hydrocarbon is:
 (3)
(3)
The mole number of cumulative injected gas is:
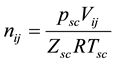 (4)
(4)
where, Vj is the pore volume in the process of production; Vij is the volume of injected gas; Z2 is the two-phase deviation factor.
Produced condensate gas will become dry gas and condensate oil after the separator, translate the number of condensate oil as gas volume [11] , thus the amount of produced hydrocarbons as follows:
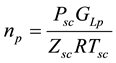 (5a)
(5a)
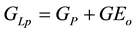 (5b)
(5b)
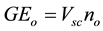 (5c)
(5c)
Plug the above equations in Equation (1), which is:
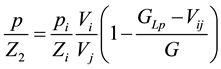 (6)
(6)
In the above equations, GLp is the cumulative production of condensate gas which includ dry gas and conversion volume of condensate oil, GEo is conversion volume of condensate oil, no is the cumulative production of condensate oil.
2.2. Introduction of Reinjection Ratio and Water Influx
As a non-ignorable factor in water drive gas reservoir, we must consider the influence of water invasion in the application of material balance method. With the exploitation of gas reservoir, water from water bodies flows into stratum, part will output and the rest still remain in the pore space. If we neglect the elastic expansion volume of rock and bound water, there is an equation about voids volume:
 (7)
(7)
Assuming that hydrocarbons exist as vapor phase in the strata under the original condition, the original pore volume of gas can be written as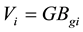 . We define the volume coefficient of remanent water as the ratio of the water storage in to the cubage, which is:
. We define the volume coefficient of remanent water as the ratio of the water storage in to the cubage, which is:
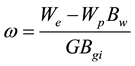 (8)
(8)
Then,
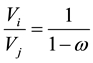 (9)
(9)
where, We is the cumulative water influx rate, Wp is the cumulative production of water, Bw is the water volume factor, Bgi is the original oil volume factor.
Combine Equation (6) with Equation (9), then the expression is:
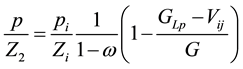 (10)
(10)
Reinjection ratio is volume ratio of injected dry gas vs. total produced gas. Research and practice show that with the increase of reinjection ratio, some medium weight hydrocarbons transfer from oil to gas, the recovery of condensate oil improved. The volume ratio of accumulative production of dry gas vs. condensate gas is Rv, and K is the reinjection ratio, therefore, we get Equation (11).
 (11)
(11)
We define an apparent reinjection ratio as , that the equation can be simplified further:
, that the equation can be simplified further:

With the growing water influx, the nonlinear degree of Equation (12) becomes higher. Change the equation as a linear relationship of 





2.3. Optimizing Solution
There are many methods can be used to obtain water influx [12] , but the process is complicated and apt to have deviation. In order to make the solution easier, new parameter, apparent relative pressure, is introduced to avoid using water influx.


There is a statistical relationship between 


We define 


Assuming a series of A, B values to seek an optimal fitting between the measured values and the predicted ones. When the deviation value is the minimum, we get the best fitting. Using the values of A and B can calculate the reserves and water influx.

Least squares method is widely used in curve fitting. To solve Equation (17) is equivalent to solve Equation (18).

The Newton iteration method and the steepest descent principle are conventional solutions for unconstrained problem, but their application ranges are different. To solve this problem, we introduce the levy berg algorithms into the solution, which is a combination of the two methods.



where, 

Plug the A value get from each iteration into Equation (17) to calculate the deviation, when the deviation reach the minimum, we get the optimal result.
3. Example and Results
The condensate gas reservoir of YH-23 located at the bottom of the paleogene and the top of the cretaceous, characterizing with high formation pressure, high dew pressure and high condensate oil content. The initial pressure is 56.11 MPa that is close to the critical state where saturation pressure is approach to maximum retrograde condensate pressure, and the phenomenon of retrograde becomes more obvious as pressure drops down. In order to maintain the formation pressure and enhance the oil recovery, cyclic gas injection has been lasting for 14 years. The temperature is 137˚C and gas bearing area is 24.5 km2 and the porosity is 13.9%. By the end of 2013, related production data are given in Table 1.
With the method proposed in the paper, we get an optimal fitting of measured values and predicted values of the apparent relative pressure, the fitting-curve is provided in the Figure 1, and the results are listed in Table 2.
3.1. Calculation of Reserves
According to the method in this paper, the reserves can be obtained by parameter A, and the calculation formula is Equation (20). We use three different methods to determine the reserves, the proven geological reserve is provided as a counterpoint, the final results are shown in Table 3.
Figure 1. The fitting-curve of the gas condensate reservoir.
Table 1. Production data of the condensate gas reservoir.
Table 2. The fitting result of the gas condensate reservoir.

As can be seen from Table 3, the number 1 is the proven geological reserve, and the number 2 - 4 are reserves calculated by three different methods. Comparing the results in the Table 3, we can find that method 2 has largest error and the suggested method has smallest error. To analyze the three methods, method 2 assumes that the gas reservoir has closed boundary and constant volume, which is the primary reason of error. Although the method 3 has significant improvement than method 2, the computed result is on the large side because of the calculation error of water influx. In contrast to the previous approaches, the application of the suggest method is more convenient and the result is more accuracy.
3.2. Prediction and Analysis of Water Invasion
According to the Equation (8) and the Equation (15), the water influx rate can be determined by parameter B:

Related parameters of water invasion can be calculated, which were shown in Table 4. In order to discuss the accuracy of prediction of water invasion, production data of 2010 are provided to contrast with the predicted value. As is shown in Figure 2 [14] , log interpretation indicates that gas-water contact of gas reservoir rose an
Figure 2. The log interpretation of YH23-2-H4.
Table 3. Reserves calculated by different methods.
Table 4. Predicted parameters of water invasion.
average of only three meters while single well water cone up seven meters. We can use volumetric balance formula to obtain the cumulative water influx rate, which is 1021.65 × 104 m3, the prediction result of suggested method is 1104.42 × 104 m3.
4. Conclusions
In summary, we draw the following conclusions:
1) We infer a material balance equation for dynamic reserves of condensate gas reservoir based on the law of conservation of mass, considering the influences of water invasion and injection-production differences. The structure of equation is simplified by the reinjection ratio and water influx, which is similar to the form of general material balance equation for gas reservoir.
2) The application of the optimization method avoids the use of water invasion coefficient. The results show that the fitting error and the dispersion degree of measurements and predictions of the apparent relative pressure are minor, which prove that this method is in line with the actual situation of gas reservoir and accurate in the calculation of reserves.
3) The forecast results of water invasion about the real gas reservoir by the proposed method correspond with the results of well log interpretation. This indicates that the proposed method can predict the basic parameters of dynamic water invasion accurately as well as dynamic geological reserves.
Cite this paper
YuXiong,LingWang,ZhongqianZhu,WeiXie, (2015) A New Method for the Dynamic Reserves of Gas Condensate Reservoir Using Cyclic Gas Injection Based on the Effects of Reinjection Ratio and Water Influx. Engineering,07,455-461. doi: 10.4236/eng.2015.77041
References
- 1. Vo, D.T., Jones, J. and Raghaven, R. (1989) Performance Predications for Gas Condensate Reservoirs. SPE Formation Evaluation, SPE-16984-PA.
- 2. Gus Alvarado, J.L., Le Blanc, F. and Farshad, F. (1992) A New and Improved Material Balance Equation for Retrograde Gas Condensate Reservoirs—Part I. SPE Rocky Mountain Regional Meeting, Casper, Wyoming, 18-21 May 1992, SPE-24355-MS.
- 3. Hsieh, F.S., Vega, C. and Vega, L. (2002) Material Balance as a Horizontal Line for a Gas-Condensate Reservoir. SPE Gas Technology Symposium, Calgary, 30 April-2 May 2002, SPE-75516-MS.
http://dx.doi.org/10.2118/75516-MS - 4. Nasiri Ghiri, M., Nasriani, H.R., Sinaei, M., et al. (2015) Gas Injection for Enhancement of Condensate Recovery in a Gas Condensate Reservoir. Energy Sources, Part A: Recovery, Utilization and Environmental Effects, 37, 799-806.
http://dx.doi.org/10.1080/15567036.2011.596901 - 5. Moradi, B., Tangsiri Fard, J., Rasaei, M.R., et al. (2010) Effect of Gas Recycling on the Enhancement of Condensate Recovery in an Iranian Fractured Gas Condensate Reservoir. Trinidad and Tobago Energy Resources Conference, Trinidad, 27-30 June 2010, SPE-132840-MS.
- 6. Smith, L.R. and Yarborough, L. (1968) Equilibrium Revaporization of Retrograde Condensate by Dry Gas Injection. Society of Petroleum Engineers Journal, 8, 87-94.
http://dx.doi.org/10.2118/1813-PA - 7. Torrens, R., Mohamed, M.E., Al Bairaq, A., et al. (2014) Integrated Asset Modeling of a Gas Condensate Field Operating Under Gas Recycling Mode. Abu Dhabi International Petroleum Exhibition and Conference, Abu Dhabi, 10-13 November 2014, SPE-171988-MS.
- 8. Kang, X.D., Li, X.F., Li, J.S., et al. (2005) Material Balance Equation of Condensate Reservoirs Exploited by Cycle Gas Injection Considering the Injection-Production Difference. Natural Gas Industry, 25, 118-120.
- 9. Jiao, Y.W., Li, B.Z., Jiang, M.Q., et al. (2010) Material Balance Equation of Condensate Gas Reservoirs with Bottom Water in Cyclic Gas Injection and Its Application. Journal of Oil and Gas Technology, 32, 325-327.
- 10. Danesh, A. (1998) PVT and Phase Behaviour of Petroleum Reservoir Fluids. Elsevier Science Ltd., Oxford.
- 11. Chen, Y.Q. (1993) The Calculation Method an Application of Equivalent Volume of Condensate Oil. Natural Gas Industry, 13, 57-59.
- 12. Marques, J.B. and Trevisan, O.V. (2007) Classic Models of Calculation of Influx: A Comparative Study. Latin American & Caribbean Petroleum Engineering Conference, Buenos Aires, 15-18 April 2007, SPE-107265-MS.
http://dx.doi.org/10.2118/107265-ms - 13. Zhang, L.Y. and Li, J. (1998) Curve Fitting Method for Calculation of the Dynamic Reserves of Water Drive Gas Reservoir. Natural Gas Industry, 18, 26-29.
- 14. Jiang, T.W., Zhu, Z.Q., Xiong, Y., et al. (2013) Dynamic Analytic Method and Practice of Condensate Gas Reservoir Developed by Cyclic Gas Injection. Petroleum Industry Press, Beijing, 136.




