Engineering
Vol. 3 No. 6 (2011) , Article ID: 5344 , 7 pages DOI:10.4236/eng.2011.36075
Application of Hypothesis of Replacement at the Analysis of a Slow Flow of a Body by a Viscous Fluid
Department of Physics, Samara State University, Samara, Russia
E-mail: volobuev@samaramail.ru
Received March 3, 2011; revised May 24, 2011; accepted June 2, 2011
Keywords: Hypothesis of replacement, Newton’s Law for Viscosity, Body Flow, Stokes formula, Resistance, Oblong Ellipsoid, Flat plate
ABSTRACT
On the basis of hypothesis of replacement and the vector formula of Newton’s law for a viscous fluid the way of a finding of resistance a slow flow by an incompressible fluid of bodies of the various form is represented. Application of an offered way to calculation of a flow of various bodies is shown: a sphere, a cylinder, an oblong ellipsoid, a flat plate. Comparison with results of other authors is given.
1. Introduction
Finding of resistance to a flow of bodies a viscous fluid the important problem for shipbuilding, aircraft, designing of devices for heat exchange, etc.
Therefore the finding of simple formulas is of interest for resistance to a slow flow of the cylinder, sphere, oblong ellipsoid, spheroid, etc. Except for formula Stokes for resistance to a flow of a sphere, the formula for other bodies at different authors considerably differ from each other.
The method for finding the force of the resistance to the flow around the cylindrical form with an arbitrary basis in based on the vector form of Newton’s law for the viscous friction in [1]. However, in some special cases, the vector form of Newton’s law for the viscosity allows the use of a simple method for solving the problems of the slow fluid flow of the body. On the basis of this method some from these tasks are below considered: a flow of the sphere, a flow of the cylinder, a flow of the oblong ellipsoid. Comparison of results of the decision with other authors is shown.
2. Hypothesis of Replacement
Let’s consider the following hypothesis which further we shall name a hypothesis of replacement.
Force of resistance to a slow flow of a body a viscous fluid is proportional to volume of the fluid superseded by a body, both due to replacement of a fluid by a body, and due to hydrodynamics of a boundary layer about a body.
Let W is a volume of the fluid superseded by a body. We count, that force of friction of a fluid about a body is proportional to volume of the superseded fluid 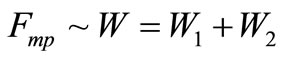 , where
, where 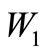 - the volume of a fluid superseded by a body,
- the volume of a fluid superseded by a body,  - the volume of a fluid superseded owing to hydrodynamics of a boundary layer about a body.
- the volume of a fluid superseded owing to hydrodynamics of a boundary layer about a body.
Check of a hypothesis it is spent for two limiting cases. First, for a flow so-called volumetric bodies where the relation of volume of a body to a surface is great. First of all, for a sphere, where . Second, for a flow of bodies with small (in a limit zero) the relation of volume of a body to its surface, in particular, for a flat plate, where
. Second, for a flow of bodies with small (in a limit zero) the relation of volume of a body to its surface, in particular, for a flat plate, where .
.
3. Slow Flow of the Sphere by a Viscous Fluid
Slow steady flow of the sphere by a viscous fluid was investigated for the first time by Stokes in 1851 [2]. The solution of the Stokes’ problem allows to get the result of the exceptional importance [3]. This is due to the fact that the result of this decision may be used in many fields of science. However, the derivation of Stokes formula, despite its simplicity, is rather cumbersome and not transparent. Therefore, in major monographs, it is either not given [4], although the formula is used, or derivation is not in its full form [5].
We will describe a simple and physically clear way to obtain the Stokes formula and the formula for the resistance of the cylinder in the flow, based on the vector form of Newton's law for a viscous fluid [1].
The vector form of the impulse momentum equation for incompressible fluid was found in [1]. This form is valid for arbitrary direction of the fluid velocity V:
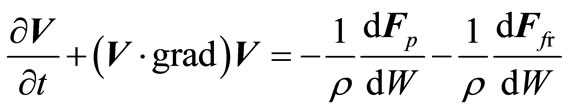 , (1)
, (1)
where 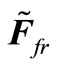 - the frictional force of fluid on the surface of a streamlined body,
- the frictional force of fluid on the surface of a streamlined body, 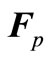 - the force, driving fluid,
- the force, driving fluid, 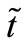 - time,
- time, 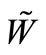 fluid volume,
fluid volume, 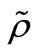 fluid density.
fluid density.
In [1] also shows that the differential force of friction for incompressible fluid can be written as:
 , (2)
, (2)
where S – vector of the contact area of the fluid and the body, h - dynamic viscosity of the fluid.
First, we will consider a slow steady sphere flow by the fluid with velocity v, figure 1, using the equations (1) and (2). In this case, using the standard approximation for the Stokes problem [3], equation (1) takes the form:
 . (3)
. (3)
We will distinguish, as we follow [3], the belt area on the surface of the sphere:
 , (4)
, (4)
where R – the radius of the sphere, q - angle at which the belt is located on the sphere.
When the fluid flows around the sphere, angular velocity vector of fluid particles w, flowing around the sphere, is always perpendicular to the general differential vector of the belt area dS, figure 1. Therefore
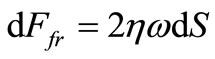 . (5)
. (5)
This equation (5) takes into account that  [4].
[4].
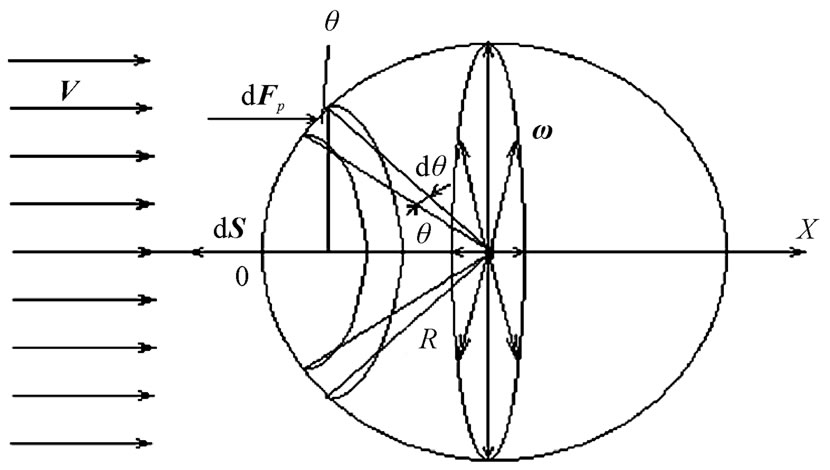
Figure 1. The scheme of the sphere flow by the fluid flow in order to find the Stokes formula.
Let us find the right part of equation (3) in the scalar form:
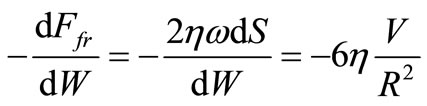 . (6)
. (6)
To find (6) we used the following formulas: 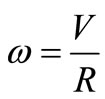 and
and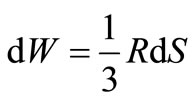 . The minus sign reflects the fact that the friction force
. The minus sign reflects the fact that the friction force  is directed against the force
is directed against the force 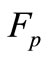 driving the fluid. We shall note, that have neglected a boundary layer, therefore at a flow of a sphere one value of linear speed V is considered only.
driving the fluid. We shall note, that have neglected a boundary layer, therefore at a flow of a sphere one value of linear speed V is considered only.
The use of the formula for the differential volume dW is defined as follows. In equation (1) volume W, in the denominator term, which determines the friction in the fluid, is covered by the surface area S, which is used in formula (2). Surface elements of volume 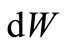 that aren’t flowed round by the fluid and the fluid velocity which is perpendicular to them, may not be considered. Therefore, the area of the belt on the sphere dS corresponds to the volume of the cone dW, the base of which is the belt dS.
that aren’t flowed round by the fluid and the fluid velocity which is perpendicular to them, may not be considered. Therefore, the area of the belt on the sphere dS corresponds to the volume of the cone dW, the base of which is the belt dS.
W – is volume of the superseded fluid, as in Arhimed’s law. Force of friction is proportional to volume of the superseded fluid . In given section
. In given section . If volume
. If volume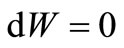 , force of friction
, force of friction
 . Otherwise in the equation (1)
. Otherwise in the equation (1)  that is impossible.
that is impossible.
We will find the scalar form of the left side of equation (3):
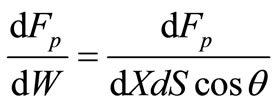 . (7)
. (7)
In (7) we take into account that the force 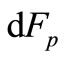 acts in the direction of the coordinate axis X on the area
acts in the direction of the coordinate axis X on the area .
.
Equating (6) to (7) and using (4), we find:
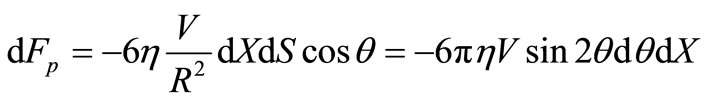 . (8)
. (8)
Integrating (8) according the angle q and the coordinate X, we have:
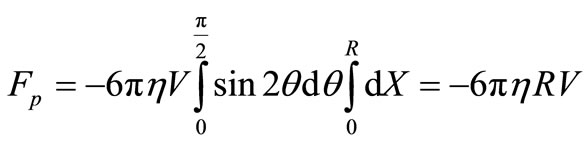 . (9)
. (9)
When setting the limits of integration we take into account that the force  acts on the left side of the sphere, figure 1. The beginning of X-coordinate is taken on the surface of the sphere on the left side.
acts on the left side of the sphere, figure 1. The beginning of X-coordinate is taken on the surface of the sphere on the left side.
Since the resistance force of the fluid movement from the sphere - Stokes force - is equal to the force , we can write:
, we can write:
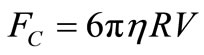 . (10)
. (10)
4. Slow Flow of the Plate by a Viscous Fluid
Let’s analyse, using a hypothesis of replacement a slow flow of a flat plate by the viscous fluid, figure 2.
Let’s find the right part of the equation (3) for a thin flat plate in width b, streamline along an axis X from two sides. Obviously, in this case all replacement is carried out due to hydrodynamics of a stream and .
.
Force of friction at a flow, taking into account two sides of a plate, is equal:
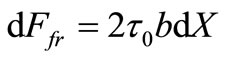 , (11)
, (11)
where 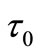 - stress of friction on a plate. Using [5], we shall write down:
- stress of friction on a plate. Using [5], we shall write down:
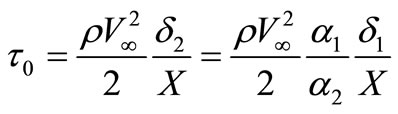 , (12)
, (12)
where  - speed of a fluid far from a plate,
- speed of a fluid far from a plate,
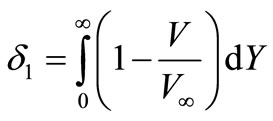 - thickness of replacement (Y – coordinate across plates),
- thickness of replacement (Y – coordinate across plates), 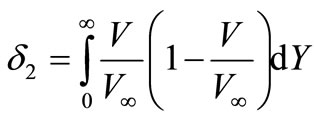 - thickness of loss of the impulse. Sizes
- thickness of loss of the impulse. Sizes  and
and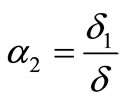 , where d - thickness of a boundary layer, figure 2.
, where d - thickness of a boundary layer, figure 2.
Substituting (12) in (11), we shall find:
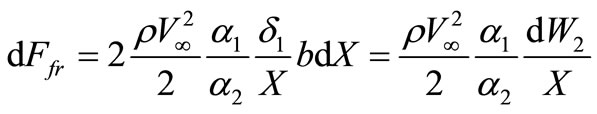 . (13)
. (13)
For a flat plate elementary volume of replacement
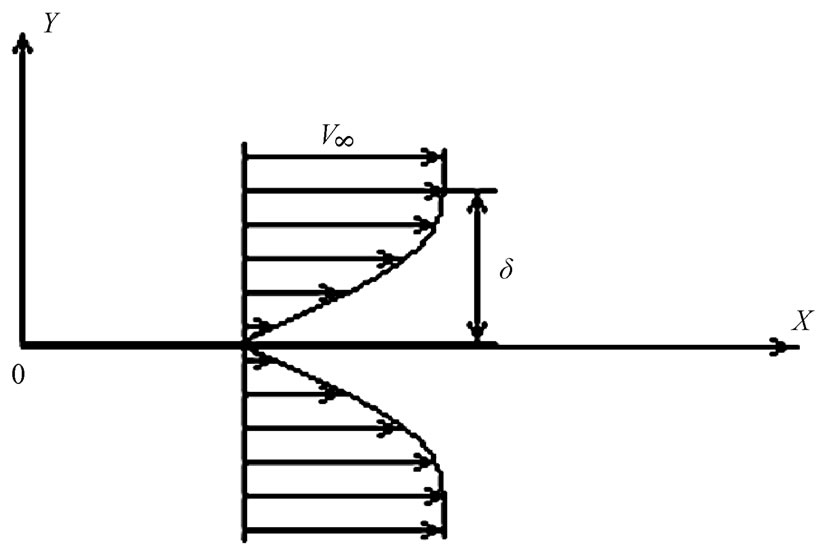
Figure 2. The scheme the flow of the flat plate flow by the viscous fluid.
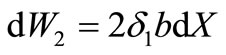 . The factor takes into account two, that replacement of a fluid goes from both sides of a plate. As
. The factor takes into account two, that replacement of a fluid goes from both sides of a plate. As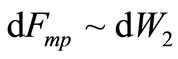 , that, actually, the hypothesis of replacement for a plate is proved. We shall show also, that the further transformations result in correct results.
, that, actually, the hypothesis of replacement for a plate is proved. We shall show also, that the further transformations result in correct results.
The right part of the equation (3), taking into account , for a plate looks like:
, for a plate looks like:
 . (14)
. (14)
Comparing (12) and (14), we find:
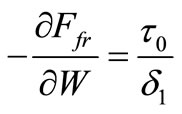 . (15)
. (15)
If to enter a gradient of pressure  and to take into account, that for an element of volume of a fluid
and to take into account, that for an element of volume of a fluid
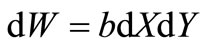 then differential of driving force
then differential of driving force
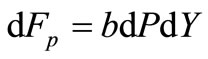 and
and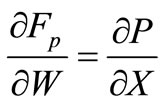 . Hence, from (3) and (15)
. Hence, from (3) and (15)
we shall find:
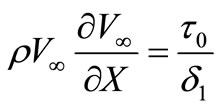 . (16)
. (16)
The known formula for flow in a boundary layer
 [5] is used. The received equation (18)
[5] is used. The received equation (18)
represents the equation of impulse as, found in [5], for a flow of a flat plate:
 , (17)
, (17)
under condition of neglect the first composed in the right part (a slow flow).
Thus, use of a hypothesis of replacement for a flat plate results in correct results.
Proceeding from (11) and using (16), we shall find force of friction of a fluid about a plate at its slow flow:
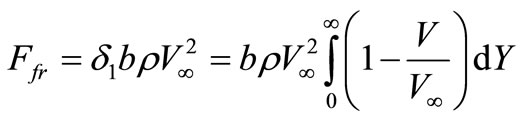 . (18)
. (18)
For a finding of resistance of a plate of a flow fluid the knowledge of size , i.e. actually forms of a structure of speed
, i.e. actually forms of a structure of speed  is necessary. If to use a structure of speed as a polynom of the fourth degree [5], thickness of replacement
is necessary. If to use a structure of speed as a polynom of the fourth degree [5], thickness of replacement , where l - length of a plate. Hence, for a slow flow of a plate force of friction:
, where l - length of a plate. Hence, for a slow flow of a plate force of friction:
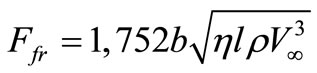 . (19)
. (19)
Let’s note, that in a result force of friction appeared proportional not the areas of a plate, and size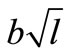 .
.
5. Slow Flow of the Long Cylinder by a Viscous Fluid
For a long cylinder, which is located across the flow, the flow problem can not be solved, even for very low Reynolds numbers, ignoring the inertial (nonlinear) terms of the momentum equation (1). In the case of writing Newton's law for a viscous fluid in the standard form there is a problem with the boundary conditions for the velocity at large distances from the body [6]. Accounting of inertial terms allows us to solve the problem [7], but, in fact, it is now in the nonlinear approximation. We will show the way to use the vector form of Newton’s law for a viscous fluid in the form (2), applying the used methodology for solution of the problem of cylinder flow by the viscous fluid, in the linear approximation, figure 3.
Now we will consider the fluid flow around a cylinder having an arbitrary profile in a cross section and a center of symmetry.
We distinguish the unit area on the surface of the cylinder:
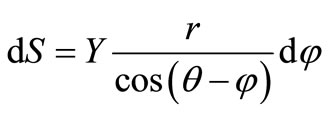 , (20)
, (20)
where r - variable radius of the cylinder, j - angle at which the platform is located on the cylinder, q - angle determining the position of the tangent to the section of the cylindrical form, Y - the length of the cylinder.
When the fluid flows around the cylinder, the vector of the angular velocity of the fluid particles w, a streamlined cylinder, is directed along the axis of the cylinder and is always perpendicular to the vector of the differential area dS, figure 3. Therefore, the modulus of the friction force is equal to:
 . (21)
. (21)
Let us find the right part of equation (3) in scalar form:
 . (22)
. (22)
To find (22) we used the following formulas: 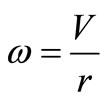 and
and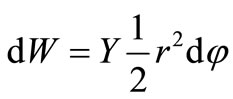 .
.
The selection principle of the volume dW is the same as the principle in the case of the flow of the sphere.
Now we will find the scalar form of the left side of the equation (3):
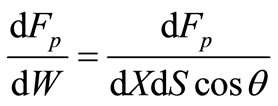 . (23)
. (23)
In (23) we take into account that the force  acts in the direction of the coordinate axis X on the area
acts in the direction of the coordinate axis X on the area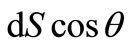 .
.
Equating (22) to (23) and using (20), we find:
 . (24)
. (24)
Integrating (24) on the angle of j and coordinate X, we have:
 , (25)
, (25)
where r0 - a half of the size of the profile in the direction of the X-axis.
When setting the limits of integration we take into ac-
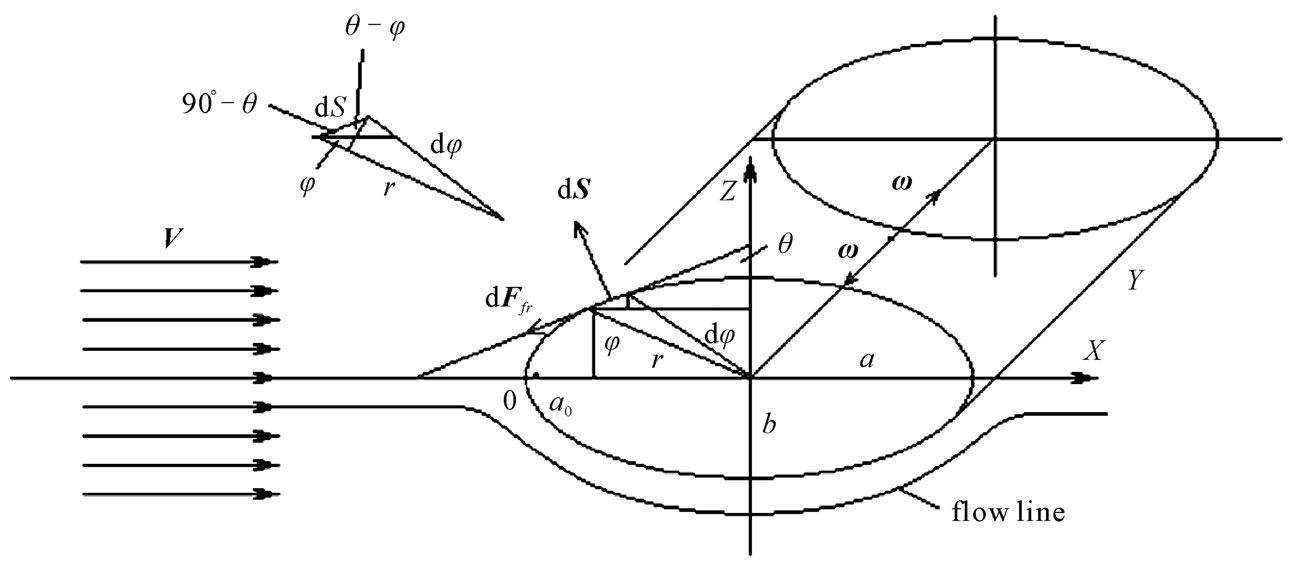
Figure 3. Scheme of a cylinder flow by the fluid flow.
count that the force  acts on the left side of the cylinder, figure 3.The beginning of the coordinate X, as well as in case of the sphere flow, is taken on the surface of the left side of the cylinder.
acts on the left side of the cylinder, figure 3.The beginning of the coordinate X, as well as in case of the sphere flow, is taken on the surface of the left side of the cylinder.
In case of a circular cylinder flow with the radius , corners
, corners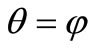 . Therefore:
. Therefore:
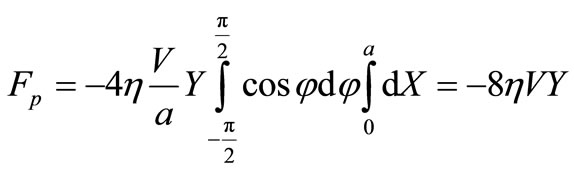 .
.
The strength of the resistance to the movement of fluid from streamline fluid of the cylinder is equal to:
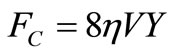 . (26)
. (26)
This formula is obtained in [1] according to another method, but it is also based on Newton’s law for a viscous fluid in the form (2).
The attention is drawn to the absence of dependence of the force 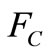 on the cylinder radius. This effect according to the analysis of dimension, is scored in [7]. It is lost in the transition to the nonlinear approximation in the calculation.
on the cylinder radius. This effect according to the analysis of dimension, is scored in [7]. It is lost in the transition to the nonlinear approximation in the calculation.
Abrupt changes in the kinetic energy flux at the inflection of the flow lines at the beginning and at the end of a cylinder flow, are mainly described by the convective nonlinear terms in the impulse momentum equation (1). Therefore, the dependence of the force 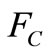 on the radius may occur only if we take into account this term, and thus the calculation of the inflection of the flow lines, which is confirmed in [7].
on the radius may occur only if we take into account this term, and thus the calculation of the inflection of the flow lines, which is confirmed in [7].
Due to the fact that the flow at the ends of the cylinder was not considered, equation (26) can be used in practical calculations only in the cases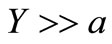 . It gives a good estimation of the resistance of the cylinder in the area Reynolds’s number
. It gives a good estimation of the resistance of the cylinder in the area Reynolds’s number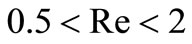 .
.
It is also important to note that due to the identity of the applied methods of finding resistance to the fluid flow of the sphere and the cylinder, the accuracy of the formulas (10) and (26) can be considered the same.
The elliptic cylinder flow is also of a great interest.
Using formula (25) and the ratio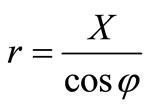 , we find:
, we find:
 .
.
In this case а – semiaxisis of the ellipse coinciding with the axis X, 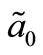 the beginning of integration over X. The position of а0 is approximately determined by the projection of an inflection point of the line flow to the X-axis, passing near the cylinder in the beginning of its flow. The exact position of the point а0 can be determined only by solving the nonlinear problem.
the beginning of integration over X. The position of а0 is approximately determined by the projection of an inflection point of the line flow to the X-axis, passing near the cylinder in the beginning of its flow. The exact position of the point а0 can be determined only by solving the nonlinear problem.
The relationship between the angles q and j can be easily found on the basis of the geometric meaning of the derivative of the ellipse equation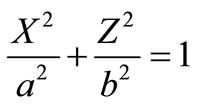 . Taking into consideration that both corners are sharp, we have:
. Taking into consideration that both corners are sharp, we have:  , where b – semiaxis of the ellipse, which is perpendicular to the flow. Unfortunately, it does not seem possible to find the force of the resistance of the elliptical cylinder as a simple computational formula similar to (26).
, where b – semiaxis of the ellipse, which is perpendicular to the flow. Unfortunately, it does not seem possible to find the force of the resistance of the elliptical cylinder as a simple computational formula similar to (26).
6. Slow Flow of Oblong Ellipsoid of Rotations by an Incompressible Fluid
Let’s consider a flow of ellipsoid of rotations by a viscous incompressible fluid. We believe, that ellipsoid’s section similar to section of the elliptic cylinder on figure 3. As well as in case of a sphere in a basis of calculation we shall put the equation (3).
Let’s allocate on a surface of ellipsoid of rotations the belt area:
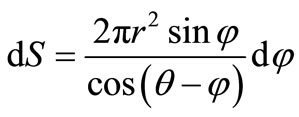 . (27)
. (27)
All designations in (27) correspond figure 3.
Force of friction on a platform 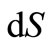 is equal:
is equal:
 . (28)
. (28)
The element of volume corresponding to this force of friction:
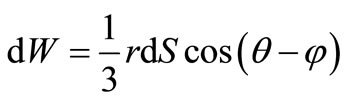 . (29)
. (29)
Taking into account , we find the scalar form of the right part of the equation (3):
, we find the scalar form of the right part of the equation (3):
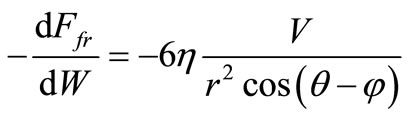 . (30)
. (30)
The scalar form of the left part of the equation (3) looks like, similar (23):
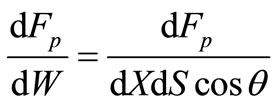 . (31)
. (31)
Equating (30) and (31), we find the force acts on ellipsoid in the direction of the coordinate axis X:
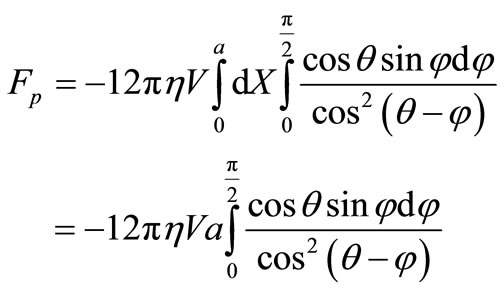 . (32)
. (32)
Force of resistance can be expressed through radius of an equivalent sphere [8]:
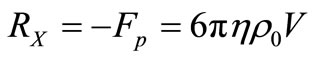 , (33)
, (33)
where in this case equivalent radius:
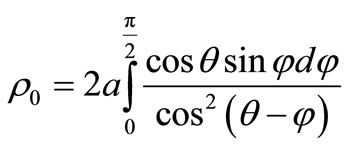 . (34)
. (34)
Size a – half-axle of ellipsoid along a stream.
Using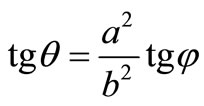 , where b – half-axle of ellipsoid of rotations perpendicular to a stream, we shall transform equivalent radius:
, where b – half-axle of ellipsoid of rotations perpendicular to a stream, we shall transform equivalent radius:
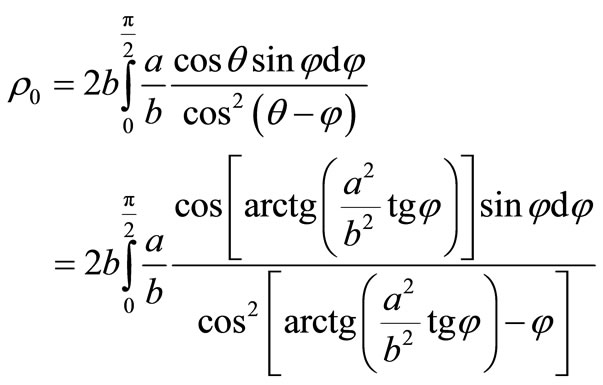 . (35)
. (35)
At 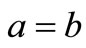 corners
corners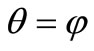 . From the formula (34) follows, that in this case
. From the formula (34) follows, that in this case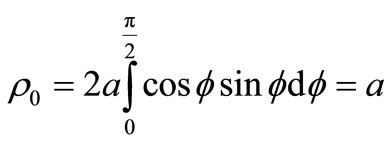 . Hencefor force of resistance (33) we receive formula Stokes (10).
. Hencefor force of resistance (33) we receive formula Stokes (10).
The integral (35) at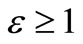 , i.e. for a oblong ellipsoid rotations, is integrated in quadratures. For this purpose preliminary we get rid from atangent with the help of the formula
, i.e. for a oblong ellipsoid rotations, is integrated in quadratures. For this purpose preliminary we get rid from atangent with the help of the formula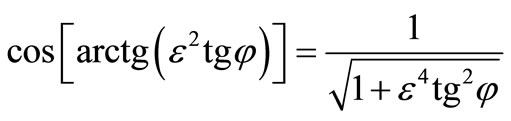 . After simple transformations the integral (35) will be transformed to a kind:
. After simple transformations the integral (35) will be transformed to a kind:
 .
.
Further substitution 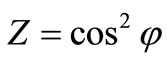 we pass to algebraic functions:
we pass to algebraic functions:
 .
.
Then, using substitution , we pass to rational algebraic functions and as a result we find:
, we pass to rational algebraic functions and as a result we find:
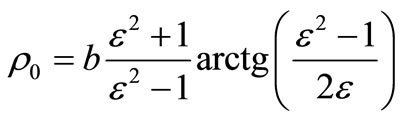 . (36)
. (36)
At , according to (36), equivalent radius
, according to (36), equivalent radius
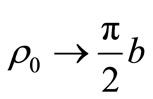 . Using (33), we shall find force of resistance of very much oblong ellipsoid rotations at its flow a viscous incompressible fluid along big half-axle:
. Using (33), we shall find force of resistance of very much oblong ellipsoid rotations at its flow a viscous incompressible fluid along big half-axle:
 . (37)
. (37)
The formula (37) has enough approached character. And force of resistance to a flow at calculation under the formula (37) appears underestimated. It is connected by that in process of lengthening ellipsoid the role of a boundary layer in replacement of a fluid grows.
Dependence of factor of resistance of ellipsoid in approach (37) from Reynolds's number looks like:
 , (38)
, (38)
where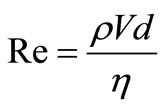 , diameter
, diameter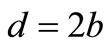 , r - density of a fluid.
, r - density of a fluid.
On figure 4 calculation under the formula (36) relative equivalent radiuses of ellipsoid rotations 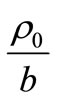 (line 1) is submitted depending on relative lengthening the form of it ellipsoid
(line 1) is submitted depending on relative lengthening the form of it ellipsoid .
.
For comparison results of calculation under the formula of authors [9]

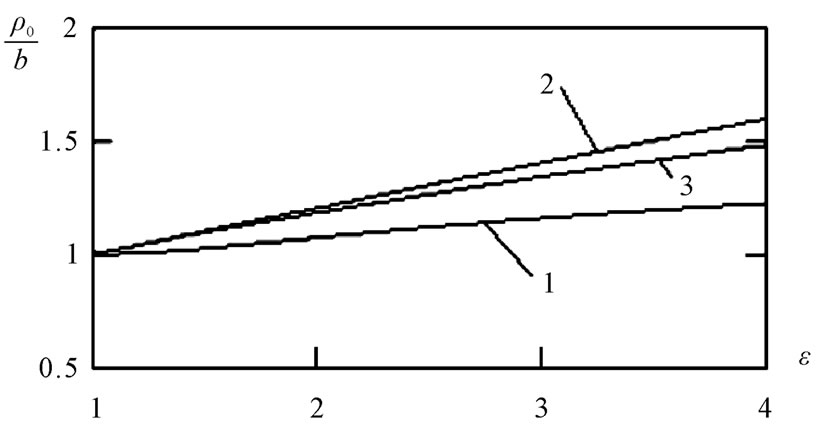
Figure 4. Calculation of relative equivalent radius ellipsoid depending on a degree of its elongation ε.
(line 2) and [10] under the formula  (line 3) are shown also.
(line 3) are shown also.
The line 1 has lower results, than lines 2 and 3. Apparently, it is connected to increasing influence of replacement of a fluid in a boundary layer in process of lengthening ellipsoid, but the final choice between the calculations resulted on figure 4 can be made only as a result of experiments.
7. Conclusions
Thus, use of a hypothesis of replacement allows to estimate resistance of bodies of the various form to a slow flow their fluid. Resistance of a body is defined by replacement of volume of a fluid, both a body, and a boundary layer on a streamline body. Therefore there is an opportunity of definition of parameters of a boundary layer. For example, calculation of thickness of replacement, at measurement the general resistance of a body to a flow and a finding of its geometrical volume. The carried out analysis shows: than it is more ratio of volume of a body to its surface, especially exact results of calculation of resistance of a body to a slow flow is possible to receive proceeding only from known geometry of a body.
8. REFERENCES
- A. N. Volobuev and E. S. Petrov, “The Research of the Flow of Bodies with Use of the Vector Form of the Newton’s Law for the Viscous Fluid,” Engineering, No. 3, 2011, pp. 162-167.
- G. G. Stokes, “On the Effect of Internal Friction of Fluids on the Motion of Pendulums,” Transaction of the Cambridge Philosophical Society, Vol. 9, Part 2, 1851, pp. 8-106.
- L. G. Lojtsansky, “Mechanics of a Fluid and Gas,” 7th Edition, Drofa, Moscow, 2003.
- G. N. Abramovich, “Applied Gas Dynamics,” Science, Moscow, 1969.
- G. Schlichting, “Theory of a Boundary Layer,” Science, Moscow, 1974.
- G. K. Batchelor, “An Introduction to Fluid Dynamics,” NIC, Moscow-Izhevsk, 2004.
- L. D. Landau and E. M. Lifshits, “Hydrodynamics,” Science, Moscow, 1986.
- H. Lamb, “Hydrodynamics,” Gostechizdat, Moscow, 1947.
- D. Happel and G. Brenner, “Hydrodynamics at Reynolds’s Small Numbers,” World, Moscow, 1976.
- I.V. Dudin and R. K. Narimanov, “Resistance at Slow Movement Ellipsoid,” The News of Tomsk Polytechnical University, Tomsk, Vol. 307, No. 3, 2004, pp. 17-21.

