Engineering
Vol. 3 No. 1 (2011) , Article ID: 3737 , 4 pages DOI:10.4236/eng.2011.31010
Theoretical Basis for Multiple Criteria Analysis of Variants and Selection of the Most Effective Technological Scheme for Hard Rock Surface Mining
Department of Chemical & Mining Engineering, College of Engineering & Technology, University of Dar es Salaam, Dar Es Salaam, Tanzania.
E-mail: massaweantipas@hotmail.com, mussaco@gmail.com
Received October 2, 2010; revised November 23, 2010; accepted November 26, 2010
Keywords: Level, Alternative Variants, Technological Schemes, Selection, Competent Variants
ABSTRACT
The technological scheme of a hard rock surface mine is a multiple level production system of interdependently functioning elements. Selection of the optimum combination of its elements constitutes a complex multiple variant and criteria problem of decision making. In this paper describes the theoretical part of the method proposed for the quantitative analysis and selection of the most competent technological schemes, based on the mathematical formulations of the selection criteria of the element of each level as functions of the alternative variants of the elements of the level and its adjacent levels. It is realized in accordance to standard procedures of decision making in the formation of the economical mathematical model of the cumulative influence of levels and elements on the effectiveness of all alternative variants in their analysis and generation of a small subset of the most competent variants, which are subjected to further analysis using the criterion of reliability in the generation of the optimum technological scheme. The scientific challenge inherent in its realization constitutes a PhD research opportunity for those interested in the problems of optimization in hard rock surface mines.
1. Introduction
The technological scheme of a hard rock surface mine represents a multiple level production system of interdependently functioning elements of mine design, equipment, mechanisms and processes [1,2]. The number of its alternative variants is huge and all exhibiting variable effectiveness in any class of mining and geological conditions. Selection of the most effective element for each level involves several conflicting criteria and the development and operation of the system is associated with huge capital and operational costs in the acquisition and exploitation of the expensive, but highly productive mining equipment and mechanisms. Therefore, it is necessary to consider all alternative variants and important criteria in the selection of the system elements most compatible in accordance to their production and/ other functional capacities and fitness in the given class of mining and geological conditions because this is the best way to achieve the maximum utilization of production capacities and justify investment in the hard rock surface mining industry. The methods available for the selection of solutions in hard rock surface mining don’t consider all possible variants and necessary criteria and most of them dwell on separate elements of the system in isolation [3-11]. The standard procedures of decision making successfully tested in the multiple criteria analysis of all possible variants and selection of the most effective parameters of underground coal mines in Bangladesh [12] and Tanzania [13] could be used to enhance effectiveness in the selection of technological schemes for hard rock surface mines as well.
2. Description of the Method
The selection method proposed in this paper is based on the structural model of the alternative variants of the most prospective technological schemes of hard rock surface mines and the mathematical formulations of criteria in the selection of the element of each level as functions of the alternative variants of elements for the level and its adjacent levels. The method is realized in accordance to standard procedures of decision making in the computer aided formation of the economical mathematical model of the cumulative influence of levels and their alternative variants of elements in the analysis and generation of a small subset of most competent technological scheme (s) of hard rock surface mines in any class of mining and geological conditions. The small subset is subjected in the generation of optimum variant.
2.1. The Structural Model of the Alternative Variants of the Technological Schemes of Hard Rock Surface Mines and the Selection Criteria
The alternative variants of the most prospective technological schemes of hard rock surface mines and the criteria considered in the optimum selection of the most effective element for each of the levels could be presented in the form of the structural model illustrated in Table 1.
The model is developed based on viewing the technological scheme of a hard rock surface mine as a complex production system of interconnected and interdependently functioning levels, each level having a definite number of alternative elements. The model shows that the alternative variants of the most prospective techno-

Table 1. Model of alternative variants and the criteria of selection.
logical scheme of a hard rock surface mine fit for any class of mining and geological conditions could be more than hundreds of thousands. Selection and optimization of the technological schemes of hard rock surface mines in any class of mining and geological conditions involves a huge number of alternative variants and several conflicting criteria in the selection of element for each of their levels which are interdependently and stochastically functioning under the influence of numerous mining, geological and organizational factors which are different for different mines and sections of the same mine. As a consequence, it is necessary to consider reliability of elements and the system as a whole in the selection of the most competent subset of variants and their optimization and generation of the optimum variant. Therefore, selection and optimization of the technological schemes of hard rock surface mines constitutes a complex multiple variant and criteria problem of decision making which could only be solved based on the systems approach methodology and the application of quantitative methods in the complex analysis of the whole set of alternative variants and generation of a small subset of the most competent which are subjected to further complex processes of optimization per criterion of reliability and generation of the most effective variant.
2.2. Analysis and Selection of the Subset of Most Competent Variants
Analysis and selection of the subset of most competent variants is carried out based on the economical mathematical model of the cumulative influence of levels and elements of the alternative variants of technological schemes on their effectiveness and in accordance to standard procedures of decision making. Procedures in the formation of the economical mathematical model of the cumulative influence of levels and elements of the alternative variants of the technological schemes of hard rock surface mines on their effectiveness are shown on Figure 1 [12,13].
Analysis and selection of the subset of most competent variants of the technological schemes of hard rock surface mines is based on the mathematical formulations of the criteria considered in the selection of the element most fit for each level, as a function of mining and geological conditions and all alternative elements of the level and its adjacent levels. The selection criteria of element for each of the levels could be established through literature review and their mathematical formulations determined from literature sources, analytical mathematical simulation and/development of empirical from the statistical data generated by the surface hard rock mines operating in variable geological and mining conditions

Figure 1. Block scheme for the formation of economical mathematical model.
worldwide. The method is realized in accordance to the procedures given on the block scheme shown on Figure 1. The block scheme describes the sequence of procedures in the formation of the economical mathematical model of the cumulative influence of levels and elements on the effectiveness of alternative variants in the analysis and generation of the most competent technological scheme (s) of a hard rock surface mine in any class of mining and geological conditions.
All procedures in the formation of the economical mathematical model described below are standard and borrowed from the theory of decision making, except block 2 which should be worked out in accordance to specially developed formulas.
Block 1: Criteria ranking and weights establishment
Each level of the structural model of technological schemes has one or several criteria. In the presence of several criteria, they should be ranked by experts in accordance to their significance within the framework of each level. In the process of ranking the criteria of each level, expert assigns rank 1 to the criteria he considers to be most significant compared to the others and the next rank is assigned to the criteria less significant than the first one, and so on. If the ranking is carried out by several experts, the rank of i-th criteria is calculated as using formula (1):
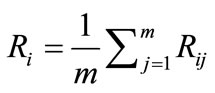 (1)
(1)
where: 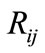 - the rank assigned to the i-th criterion by j-th expert; m - number of experts.
- the rank assigned to the i-th criterion by j-th expert; m - number of experts.
In the ranking of criteria within the framework of each level are arranged in the order of their significance, and then assigned weight 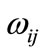 by experts. The most significant criterion is assigned weight
by experts. The most significant criterion is assigned weight 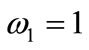 and the next criteria per significance assigned other weights
and the next criteria per significance assigned other weights 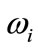 of values ranging between 0 and 1 in the order of decrement. Refinement of the weights of criteria is carried out by experts in accordance to the method of sequential comparison. If a criterion with weight 1 is more significant than the sum of other criteria, then weight
of values ranging between 0 and 1 in the order of decrement. Refinement of the weights of criteria is carried out by experts in accordance to the method of sequential comparison. If a criterion with weight 1 is more significant than the sum of other criteria, then weight 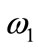 is revised in accordance to the condition expressed on formula (2).
is revised in accordance to the condition expressed on formula (2).
 (2)
(2)
where: 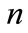 - the number criteria on the correspondent level.
- the number criteria on the correspondent level.
In case of the other way round, weight ω1 (if necessary) is reduced in accordance to the condition expressed on formula (3).
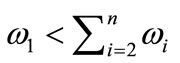 (3)
(3)
Then, similar checks are made on the remaining criteria in accordance to the order of their weights decrement (excluding the last criterion).
If the procedure of weights assignment to criteria is carried out by several experts, then the weight of criteria within the framework of each level is calculated using formula (4):
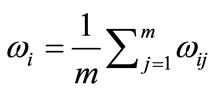 (4)
(4)
where:  - the weight assigned to the
- the weight assigned to the  -th criterion by
-th criterion by  -th expert;
-th expert; 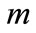 - number of experts.
- number of experts.
The standardized weight of criteria within the framework of each level is calculated using formula (5).
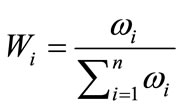 (5)
(5)
Block 2: Formulas for calculation of the absolute values of the combinations of elements of the adjacent levels of the technological schemes per each criterion
In order to establish the absolute values of the combinations of adjacent levels of the technological schemes per each criterion, the numerical values of criteria are worked out only considering the changing parameters of the examined and adjacent levels.
The value of the criteria of i-th level is generally influenced by the elements of both  and
and  levels. Consequently, the value of criteria should account for the possibility of transition along any of the
levels. Consequently, the value of criteria should account for the possibility of transition along any of the 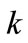 - arcs through the
- arcs through the 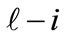 element of i-th level to any
element of i-th level to any 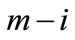 element of
element of 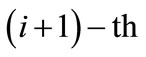 level and correspond to the values of the arcs illustrated on Figure 2.
level and correspond to the values of the arcs illustrated on Figure 2.
Block 3: Computation of Comparative values of the combinations of elements on adjacent levels
The comparative values of combinations of adjacent levels are established based on the absolute values. In doing so, the worst combination of each 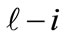 element i-th level with each m-i element
element i-th level with each m-i element 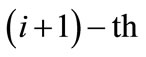 level is generated and counted basis. The comparative value of the combination of any elements of i-th level with the adjacent upper and lower levels is calculated using formulas (6) and (7).
level is generated and counted basis. The comparative value of the combination of any elements of i-th level with the adjacent upper and lower levels is calculated using formulas (6) and (7).
• When maximizing criterion:
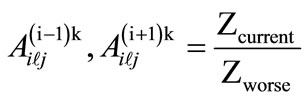 (6)
(6)
• When minimizing criterion:
 (7)
(7)
where: 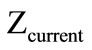 - the current value of criterion;
- the current value of criterion; 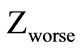 - the value of criterion at worse (basis);
- the value of criterion at worse (basis); 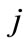 - number of criteria.
- number of criteria.
In the absence of mutual influence from adjacent levels, the comparative value of the combination of elements

Figure 2. Scheme of the formation of absolute values of the combinations of elements on adjacent levels.
from different levels is meaningless and replaced by the comparative value 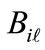 of the elements of assessed level, established from analogue formulas (8) and (9):
of the elements of assessed level, established from analogue formulas (8) and (9):
When maximizing criterion,
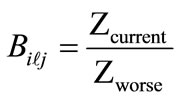 (8)
(8)
When minimizing criterion,
 (9)
(9)
Block 4: Establishment of overall value of the elements of technological schemes
The overall value of the elements of technological schemes is established by considering the weights of all criteria of the assessed level. The overall value of the combination of  element of
element of  level with
level with  element of i-th level is established using formula (10).
element of i-th level is established using formula (10).
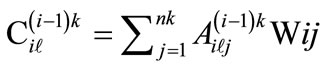 (10)
(10)
where: – Comparative value of the combination of k-th element of
– Comparative value of the combination of k-th element of 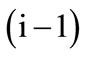 -th level with
-th level with 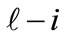 element of i-th level per
element of i-th level per  criterion;
criterion; 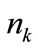 - the number of criteria of the investigated i-th level;
- the number of criteria of the investigated i-th level;  - the standardized weight of
- the standardized weight of  criterion of the i-th level
criterion of the i-th level
The overall value of the combination of m-th element of  level with
level with  element of i-th level is established using formula (11).
element of i-th level is established using formula (11).
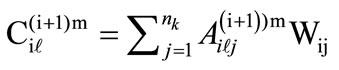 (11)
(11)
where: 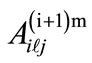 - The comparative value of the combination of
- The comparative value of the combination of 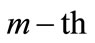 element of the
element of the -th level with
-th level with 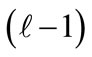 element of the i-th level per
element of the i-th level per  criterion.
criterion.
The overall value of the elements of i-th level under the mutual influence of 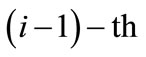 and
and 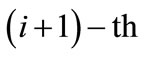 adjacent levels is calculated using formula (12).
adjacent levels is calculated using formula (12).
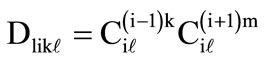 (12)
(12)
Obviously, the best combination corresponds to the maximum value of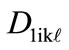 . In the absence of influence from one of the adjacent levels, the correspondent parameter in formula (12) is assigned 1. In the absence of influence from both adjacent levels, the overall value of the elements of i-th level per all criteria is established using formula (13).
. In the absence of influence from one of the adjacent levels, the correspondent parameter in formula (12) is assigned 1. In the absence of influence from both adjacent levels, the overall value of the elements of i-th level per all criteria is established using formula (13).
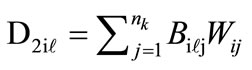 (13)
(13)
In such a way, each  element of each
element of each  level of the structural model of alternative variants of the technological schemes of hard rock surface mines presented on Table 1 is characterized by the overall values established in accordance to the relationships illustrated on formula (14) and (15)
level of the structural model of alternative variants of the technological schemes of hard rock surface mines presented on Table 1 is characterized by the overall values established in accordance to the relationships illustrated on formula (14) and (15)
• In the presence of the influence of adjacent levels:
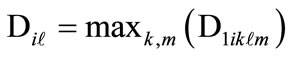 (14)
(14)
• In the absence of the influence of adjacent levels:
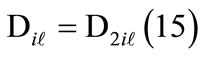 (15)
(15)
Block 5: Establishment of the weight of overall criterion for each level
Significances of the local and overall criteria of each level in the whole technological scheme are not the same. Therefore, in order to establish the real influence of levels and elements on the effectiveness of the technological schemes as a whole, it is necessary to establish the weights of the criteria of each level. The Assigning of weights to the criteria of each level could be made by experts, in accordance to the standard procedures, using formulas (1-5).
Block 6: Computation of the weighted values of elements
The weighted values of the elements of each level are calculated using formula (16):
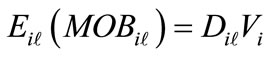 (16)
(16)
where: 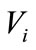 - The standardized weight of the local or overall criterion of the
- The standardized weight of the local or overall criterion of the  level.
level.
Block 7: The economical mathematical model of variants effectiveness
Includes all procedures described above and represents the algorithm for the formation of the values of arcs and nodes on the graph of alternative variants of the technological schemes of a hard rock surface mine. From the realization of this model will generate matrices of the weighted values of each element of all levels of the analyzed structural model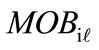 , with the help of which and on the basis of special procedures of decision making, it is possible to proceed into the formalized analysis of paths on the graph of formation of the alternative variants of the technological schemes of a hard rock surface mine. These procedures are also standard [12,13]. The weighted values of each element allows (through simple summation) to establish the comparative effectiveness of any path on the graph of the formation of alternative variants of the technological schemes of a hard rock surface mine. While considering compatibility of the elements of different levels, such path which goes through elements (graph nodes) with the maximum weighted values shall always lead into the generation of one competent variant of the technological schemes of a hard rock surface mine, counted the basis variant and having (at the average value of
, with the help of which and on the basis of special procedures of decision making, it is possible to proceed into the formalized analysis of paths on the graph of formation of the alternative variants of the technological schemes of a hard rock surface mine. These procedures are also standard [12,13]. The weighted values of each element allows (through simple summation) to establish the comparative effectiveness of any path on the graph of the formation of alternative variants of the technological schemes of a hard rock surface mine. While considering compatibility of the elements of different levels, such path which goes through elements (graph nodes) with the maximum weighted values shall always lead into the generation of one competent variant of the technological schemes of a hard rock surface mine, counted the basis variant and having (at the average value of 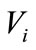 the total value of
the total value of , calculated using formula (17).
, calculated using formula (17).
 (17)
(17)
where: 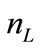 – the maximum number of levels on the structural model of variants.
– the maximum number of levels on the structural model of variants.
Generation of the other competent variants which are competitive with the basis could be made under the consideration of the variations of expert values for the significances of levels. For that purpose, it is necessary to group all levels of the technological schemes into  - subsystems, excluding the levels with one element, rank (in the order of decrement) the maximum weighted values of the elements of the levels of each subsystem and the elements of each level and, beginning with the most significant levels, sequentially compare variations of the sums of the weighted values for the basis variant, under the influence the assessed level for the optimistic and pessimistic views of experts
- subsystems, excluding the levels with one element, rank (in the order of decrement) the maximum weighted values of the elements of the levels of each subsystem and the elements of each level and, beginning with the most significant levels, sequentially compare variations of the sums of the weighted values for the basis variant, under the influence the assessed level for the optimistic and pessimistic views of experts  and
and  respectively) with the maximum possible decrement of the sums of weighted values when used for the formation of next variant of less significant elements of the assessed level. For that:
respectively) with the maximum possible decrement of the sums of weighted values when used for the formation of next variant of less significant elements of the assessed level. For that:
1) Weights are established for the optimistic 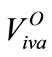 and pessimistic
and pessimistic  approaches for the level of
approaches for the level of  rank of the first subsystem
rank of the first subsystem  using formulas (18-21).
using formulas (18-21).
For the Optimistic Approach
• For the significant level:
 (18)
(18)
• For the other levels:
 (19)
(19)
For the Pessimistic Approach
• For the significant level:
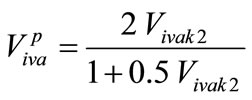 (20)
(20)
• For the other levels:
 (21)
(21)
where: 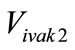 - the average value of the significant level of
- the average value of the significant level of 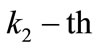 subsystem.
subsystem.
2) The new weighted values are established for the level of 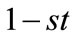 rank of the
rank of the  subsystem and the remaining levels using formulas (22,23).
subsystem and the remaining levels using formulas (22,23).
For the Optimistic Approach
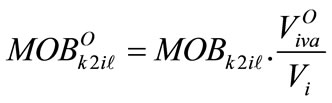 (22)
(22)
For the Pessimistic Approach
 (23)
(23)
And the transformed matrix is formed.
3) The total weighted value is established for the basis variant for the optimistic  and pessimistic
and pessimistic  using formula (17). Variations of the total weighted values for the basis variant are calculated using formula (24).
using formula (17). Variations of the total weighted values for the basis variant are calculated using formula (24).
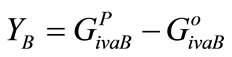 (24)
(24)
4) Shift is made to the element of 2nd rank of the level of first rank of the first subsystem and analysis of the weighted value of the element of i-st rank made. Compatibility of a picked element with the other elements of the basis variant is verified. Total weighted values are calculated and the decrement of values established using formula (25).
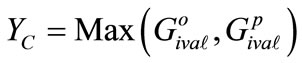 (25)
(25)
where: 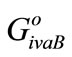 and
and 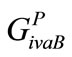 - variations of the total weighted values of the basis variant for the optimistic and pessimistic approaches respectively, established using formulas (26,27).
- variations of the total weighted values of the basis variant for the optimistic and pessimistic approaches respectively, established using formulas (26,27).
 (26)
(26)
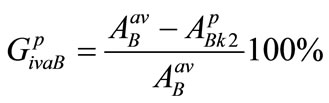 (27)
(27)
where: 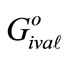 and
and 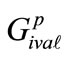 - the degree of influence of the individual elements of each significant level of each generated subsystem for the optimistic and pessimistic approach respectively, calculated using formulas (28,29)
- the degree of influence of the individual elements of each significant level of each generated subsystem for the optimistic and pessimistic approach respectively, calculated using formulas (28,29)
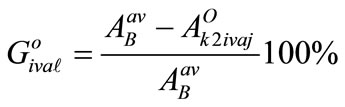 (28)
(28)
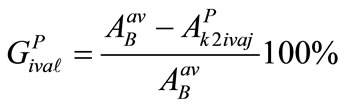 (29)
(29)
where: 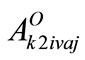 and
and 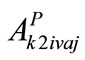 - The total weighted values in the transition to element of j-th rank of the level of 1-st rank for the optimistic and pessimistic approach respectively.
- The total weighted values in the transition to element of j-th rank of the level of 1-st rank for the optimistic and pessimistic approach respectively.
5) The difference between variations of the total weighted values is calculated. If the difference is greater or equal to the maximum decrement of values, the next variant of the technological scheme is formed.
6) Shift is made to the next subsystem  and procedures (1)-(5) repeated.
and procedures (1)-(5) repeated.
7) When subsystems for the generation of the required number of variants are all cleared, shift is made to the level of 2-nd rank of the first subsystem and procedures (1)-(6) repeated.
8) When the required number of variants (Nvar) is obtained, the final synthesis and generation of the whole subset of most competent variants of the technological scheme of a hard rock surface mine is carried out.
Realization of all procedures described above should always lead to the development of software for the computer aided analysis and selection of the subset of most competent variants of the technological scheme of a hard rock surface mine on the basis of the economical mathematical model of the cumulative influence of levels and elements of technological schemes for justification in the generation of the subset of most competent variants of technology from the whole set of alternative variants. The subset of generated variants is subjected to further detailed analysis and optimization to generate the most reliable as the most effective technological scheme of a hard rock surface mine.
3. Conclusions and Recommendations
Realization of all procedures in the method described in this paper will have both scientific and practical significance. The scientific significance includes formulation the economical – mathematical model of the cumulative influence of levels and elements on the effectiveness of the alternative variants of most prospective technological schemes of hard rock surface mines, enabling the development of software for the computer aided analysis of all alternative variants and generation of the optimum variant of the technological scheme of a hard rock surface mine. The practical significance includes the possibility of using the mathematical models and software developed in solving important practical questions in connection with the selection, justification and assessment of the economic effectiveness of the most prospective technological schemes of hard rock surface mines for the operating and new mines. The scientific challenge inherent in the realization of the method proposed in this paper constitutes a PhD research opportunity for those interested in the problems of optimization in hard rock surface mining.
4. REFERENCES
- W. Hustruli and M. Kuchta, “Open Pit Mine Planning and Design,” Taylor & Francis, London, 2006.
- B. Kennedy, “Surface Mining,” SME, 1990.
- T. Afeni, “Optimization of Drilling and Blasting Operations in an Open Pit Mining – The SOMAIR Experience,” Mining Science and Technology (China), Vol. 19, No. 6, November 2009, pp. 736-739. doi:10.1016/S1674- 5264(09)60134-4
- A. Bortolussi and R. Ciccu, S. Forte and B. Grosso, “A Contribution to a Better Design and Control of Surface Blasting,” Balkema, Rotterdam, 2000.
- S. Qu, S. Hao, G. Chen, B. Li and G. Bian, “The BLASTCODE Model: A Computer-Aided Bench Blast Design and Simulation System,” Fragblast, Vol. 6, No. 1, March 2002, pp.85-103.
- A. Mishra, “Design of Surface Blasts – A Computational Approach,” Bsc Thesis, Department of Mining Engineering, National Institute of Technology, Rourkela-769008, 2009.
- E. Bozorgrahimi, R. A. Hall and G. H. Blackwell, “Sizing Equipment for Open Pit Mining,” A Review of Critical Parameters of Mining Technology, December 2003, Vol. 112, pp. 171-179.
- R. Franke, “Combined Mining Systems for Open Pit Mines,” Bulk Handling in Open Pit Mines & Quarries, 1986, pp. 177-182.
- H. Althof, “Cost Reduction by In-Pit Crushing and Conveying,” Bulk Handling in Open Pit Mines & Quarries, 1986, pp. 205- 208.
- G. Adel, T. Kojovic and D. Thornton, “Mine-to-Mill Optimization of Aggregate Production,” Virginia, 2006. doi:10.2172/914568
- R. Zhang, Y. Zhang, T. X. Ren and B. Denby, “The Selection of Surface Mining Technology Using a Decision Making System,” Balkema, Rotterdam, 1998.
- S. K. Majimdar, “Justification and Selection of the Technological Schemes and Their Parameters for the Conditions of Underground Coal Mining in Bangladesh,” Ph.D. Thesis, Moscow State Mining University, Moscow, 1985.
- A. Massawe, “Selection of the Parameters of Development and Exploitation of Coal Faces in the Underground Coal Mines in Tanzania”, Ph.D. Thesis, Moscow State Mining University, Moscow, 1989.

