American Journal of Computational Mathematics
Vol.2 No.3(2012), Article ID:23209,5 pages DOI:10.4236/ajcm.2012.23031
The Relative Efficiency of the Conditional Root Square Estimation of Parameter in Inhomogeneous Equality Restricted Linear Model
Guangxi Normal University for Nationalities, Chongzuo, China
Email: nxl1971@sina.com
Received May 22, 2012; revised June 30, 2012; accepted July 11, 2012
Keywords: Generalized Conditional Root Square Estimation; Specific Conditional Root Square Estimation; Relative Efficiency
ABSTRACT
This paper made a discuss on the relative efficiency of the generalized conditional root square estimation and the specific conditional root square estimation in paper [1,2] in inhomogeneous equality restricted linear model. It is shown that the generalized conditional root squares estimation has not smaller the relative efficiency than the specific conditional root square estimation, by a constraint condition in root squares parameter, we compare bounds of them, thus, choose appropriate squares parameter, the generalized conditional root square estimation has the good performance on mean squares error.
1. Definition and Lemma
Definition 1 [1] In the model (1), defined as 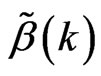 is the specific conditional root square estimation of
is the specific conditional root square estimation of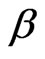 :
:
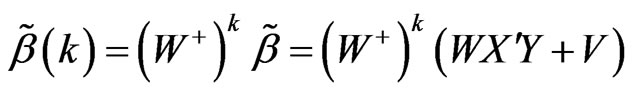 where 0 < k < 1,
where 0 < k < 1,
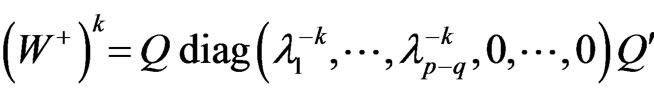 , W, V defined as above paper, Q is p-orthogonal matrix, make
, W, V defined as above paper, Q is p-orthogonal matrix, make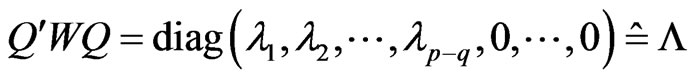 ,
, 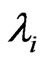 is Non-zero characteristic values of W, and
is Non-zero characteristic values of W, and 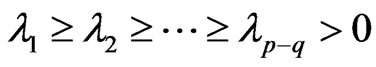 .
.
Definition 2 [2] In the model (1), defined as 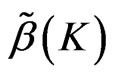 is the generalized conditional root square estimation of
is the generalized conditional root square estimation of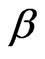 :
:
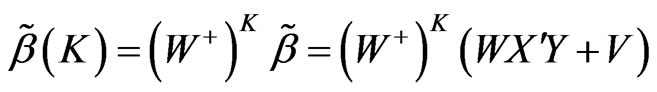 .
.
where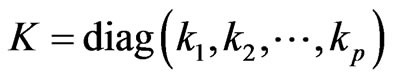 ,
,
 .
.
said 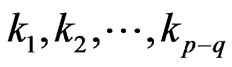 is
is 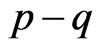 -root square parameter, W, Q, V defined as above paper.
-root square parameter, W, Q, V defined as above paper.
Definition 3 [3] Two estimation 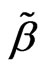 and
and 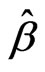 of the model (1), defined as
of the model (1), defined as 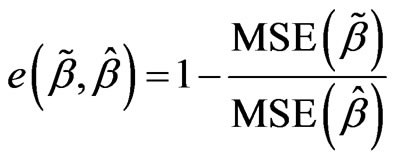 is elative efficiency of estimation
is elative efficiency of estimation 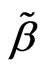 for elative efficiency estimation of
for elative efficiency estimation of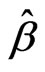 . If
. If 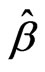 is the best linear unbiased estimation of
is the best linear unbiased estimation of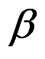 , then note
, then note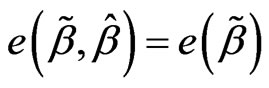 .
.
For the above definition 3, if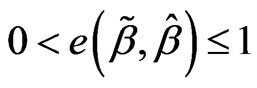 , then shows that
, then shows that  is better than
is better than 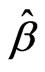 under mean squares error and if the bigger of
under mean squares error and if the bigger of 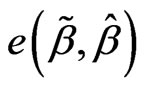 (that efficiency highter),
(that efficiency highter), 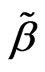 improve the degree of
improve the degree of 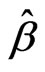 bigger.
bigger.
Lemma 1 [1]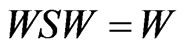 ,
,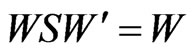 .
.
Lemma 2 [1] 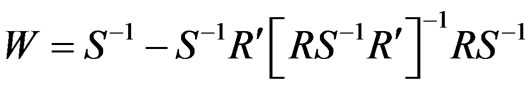 is positive semidefinite matrix, and rank of W is
is positive semidefinite matrix, and rank of W is .
.
Lemma 3 [1] Exist Q is p-order orthogonal matrix,
make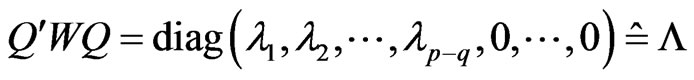 ,
,  is Non-zero characteristic values of W, and
is Non-zero characteristic values of W, and 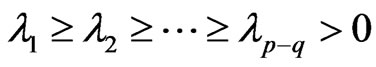 .
.
Lemma 4 [1] Mean squares error of 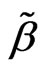 is
is
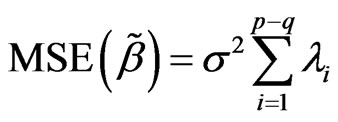 ,
, 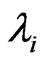 is Non-zero characteristic values of W, and
is Non-zero characteristic values of W, and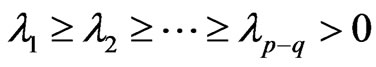 .
.
Lemma 5 [1] Assume 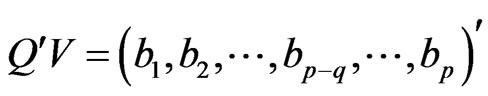 then
then
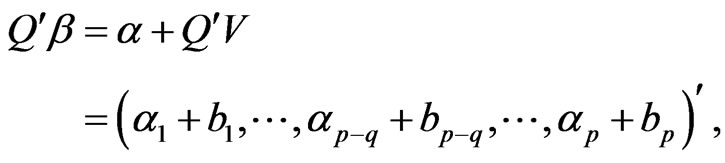
where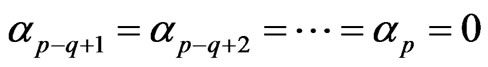 .
.
2. Main Results
We can prove the following exist theorem 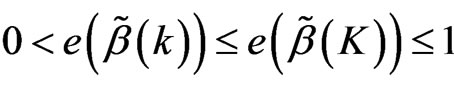 and bound of
and bound of 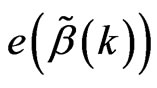 and
and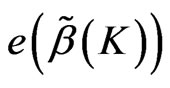 . Now, we have the following lemma.
. Now, we have the following lemma.
Assume , then
, then 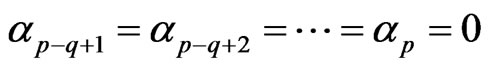 .
.
And the RLSE of  is
is
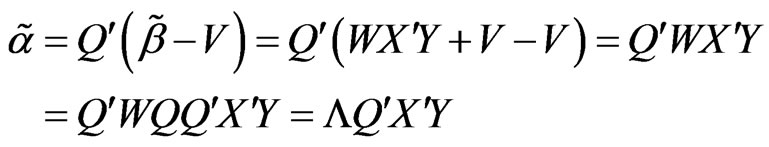
accordingly, the specific conditional root square estimation of  is
is
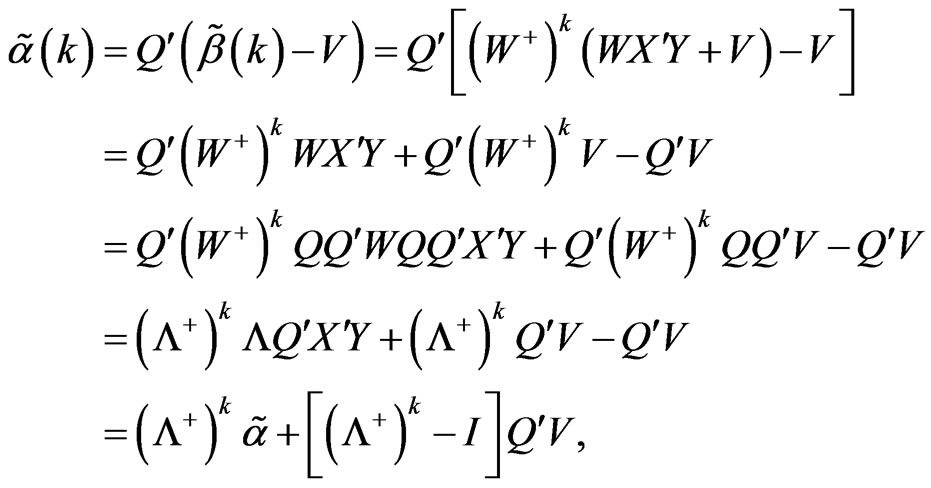
0 < k < 1.
similarly, the generalized conditional root square estimation of 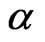 is
is
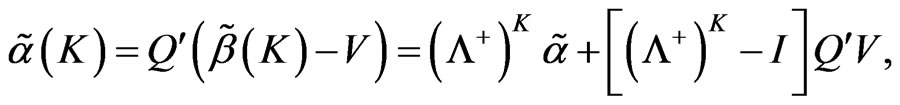
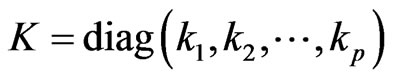 .
.
Lemma 6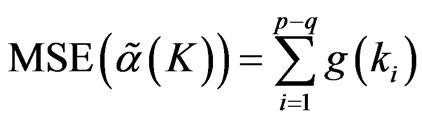 , where
, where 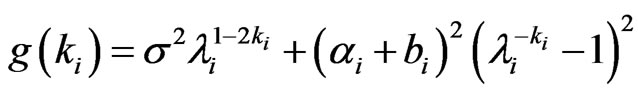 .
.
Proof:
when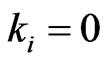 ,
,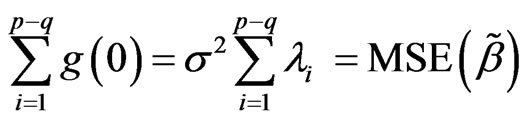 .
.
Because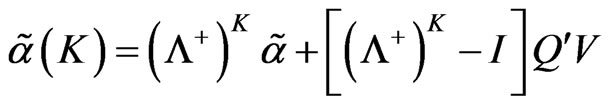 ,
,
so  .
.
Because
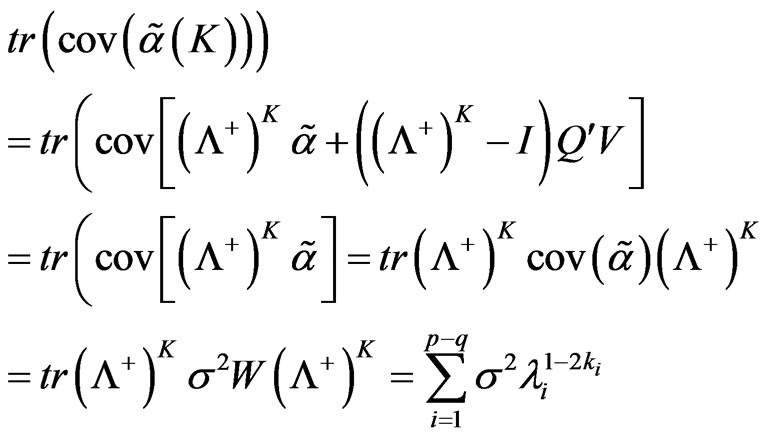
So
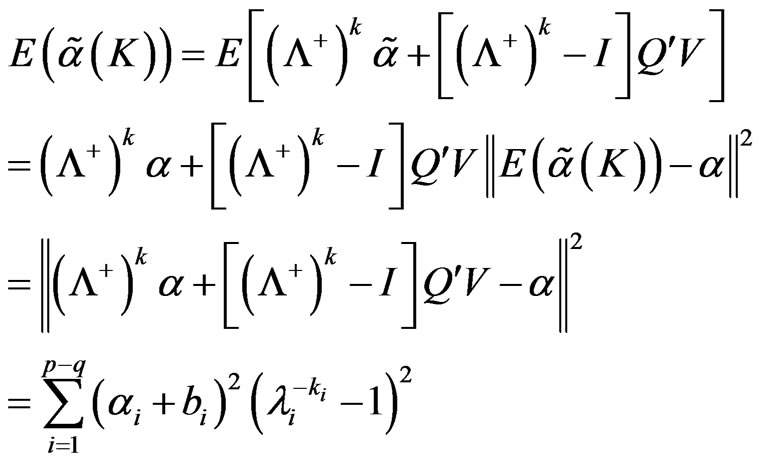
Lemma 7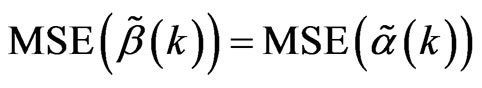 ,
,
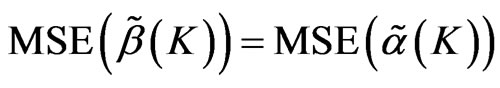 .
.
Lemma 8 When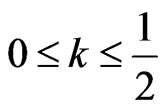 , exist
, exist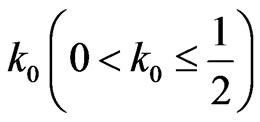 , when
, when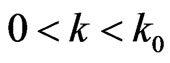 , then
, then
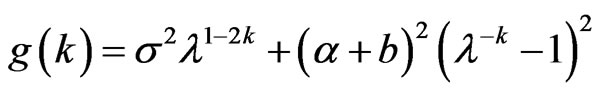
has minimum value.
Proof: Note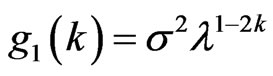 ,
, 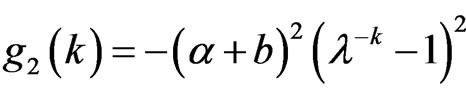 , then
, then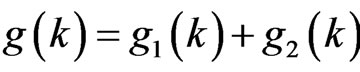 .
.
For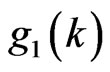 , we have
, we have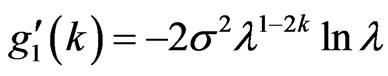 . When
. When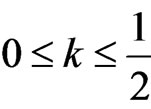 , if
, if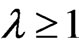 , then
, then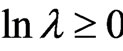 ,
,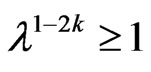 ; if
; if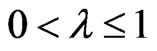 , then
, then ,
, . When
. When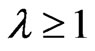 ,
, . so
. so 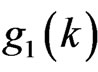 is a monotonically decreasing function in
is a monotonically decreasing function in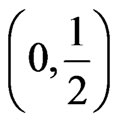 .
.
For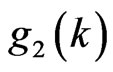 , when
, when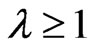 , we have
, we have
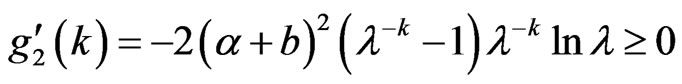 . this means
. this means
 is a monotonically increasing function in
is a monotonically increasing function in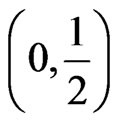 . so, there always exist
. so, there always exist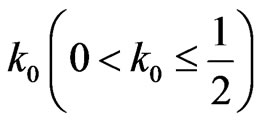 , when
, when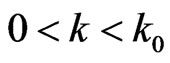 we have
we have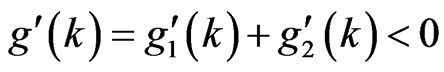 , so
, so 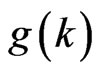 is a monotonically decreasing function in
is a monotonically decreasing function in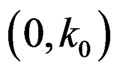 ,
, 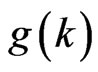 <
< ,
, 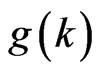 has minimum value.
has minimum value.
Lemma 9 In the model (1), for
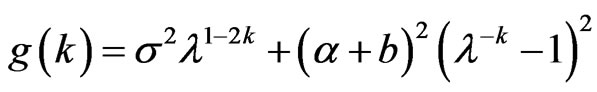 , when
, when 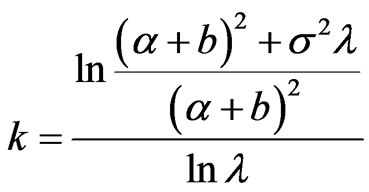 , then
, then 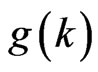 has minimum value.
has minimum value.
Proof: according to lemma 8,
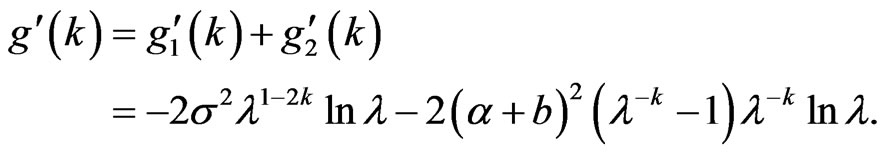
Let , we get
, we get
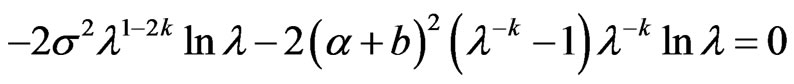 when
when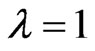 , the solution of this equation is
, the solution of this equation is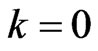 ; when
; when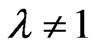 , the solution of this equation is
, the solution of this equation is
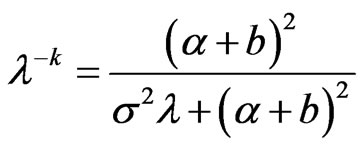 , that
, that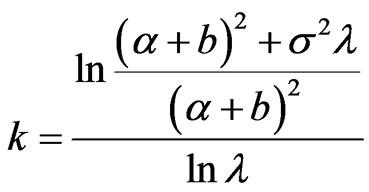 .
.
so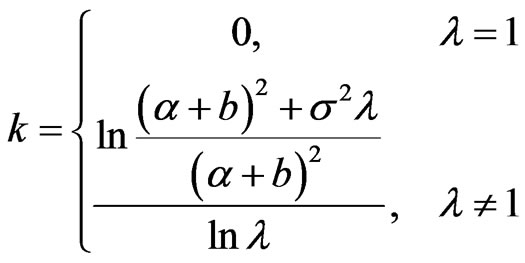 . Therefore when
. Therefore when 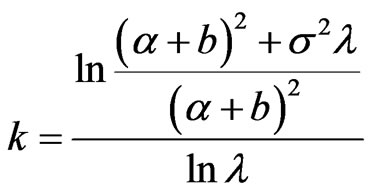 , then
, then 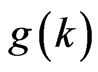 has minimum value.
has minimum value.
Lemma 10 In the model (1), exist root square parameter 0 < k < 1, then mean squares error of 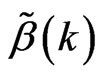 is
is
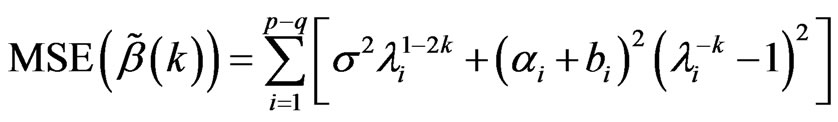 .
.
Lemma 11 In the model (1), 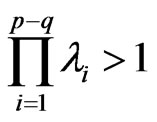 , always exist
, always exist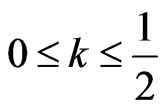 , then
, then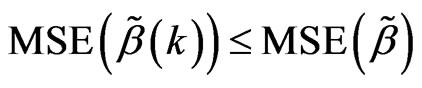 .
.
Proof: Based on the lemma 9 and lemma 10.
Theorem 1 In the model (1), 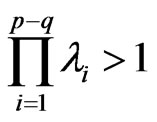 , always exist
, always exist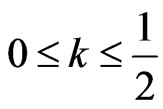 , then
, then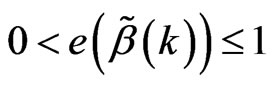 .
.
Proof: Based lemma 11 and definition 3, we get the conclusion.
Theorem 2 In the model (1), for , exist
, exist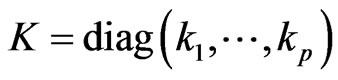 , then
, then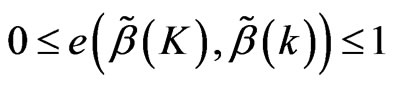 .
.
Proof: For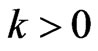 , if
, if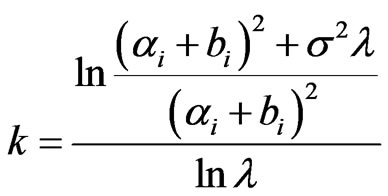 ,
,  , choose
, choose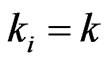 ,
,
we have 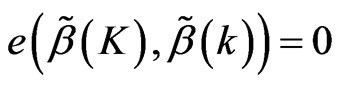 .
.
Assume at least exist i, that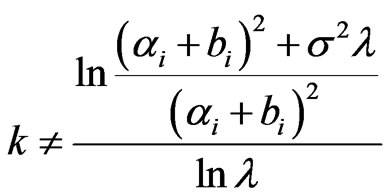 , assume
, assume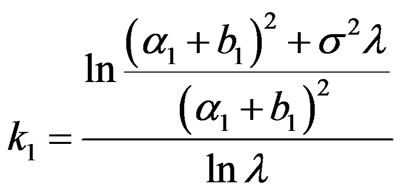 , where
, where 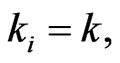
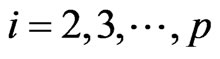 , based on lemma 6 and, we have
, based on lemma 6 and, we have
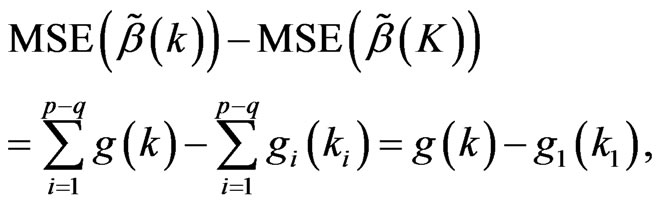
based on lemma 9, we have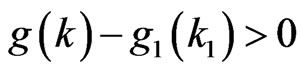 , then
, then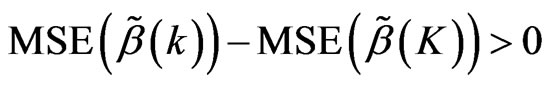 , so
, so 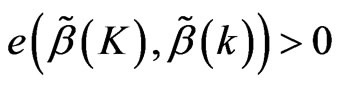 .
.
For above theorem, then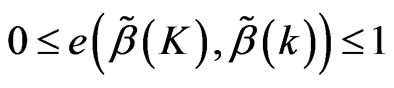 .
.
Using theorem 2, we get the following the conclusion.
Inference 1 In the model (1), for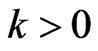 , exist
, exist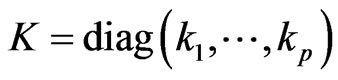 ,
,
then .
.
Inference 2 In the model (1), if 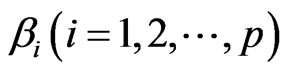 Are not all equal,
Are not all equal,
then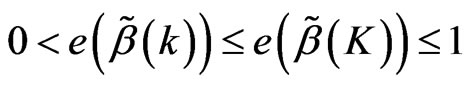 .
.
Proof: Because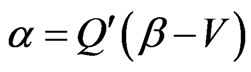 , Q is orthogonal matrix, so when
, Q is orthogonal matrix, so when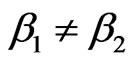 , then
, then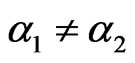 , based on theorem 2, we get the conclusion.
, based on theorem 2, we get the conclusion.
Theorem 3 In the model (1), when
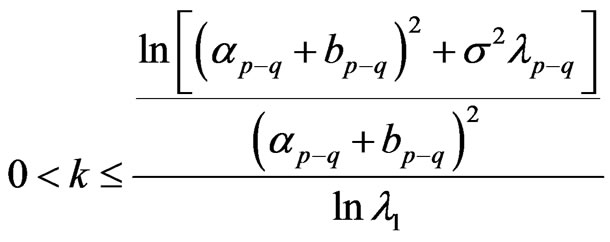 then
then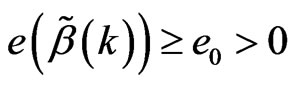 , where
, where
 ,
,
 is
is  the largest component of module.
the largest component of module.
Proof: Assume , then
, then

Assume
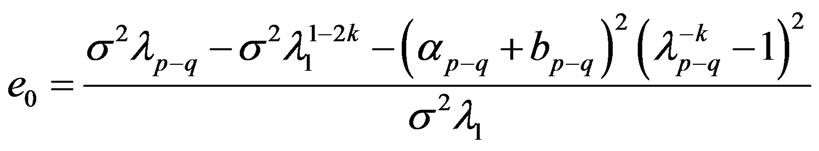 then
then
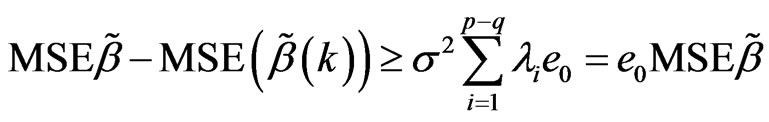 so
so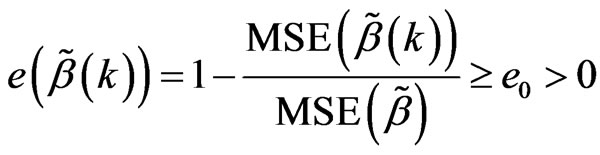 .
.
Theorem 4 In the model (1), for , if
, if 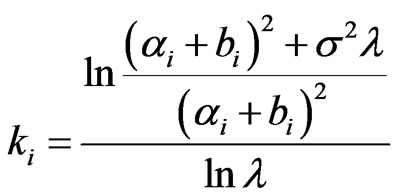
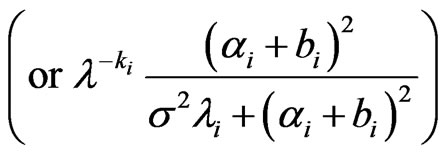 ,
, 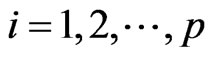 , then
, then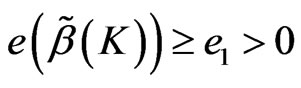 , Where
, Where
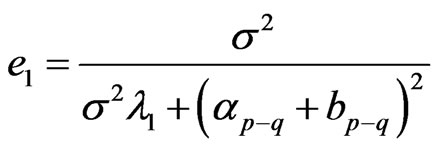 .
.
Proof:

Therefore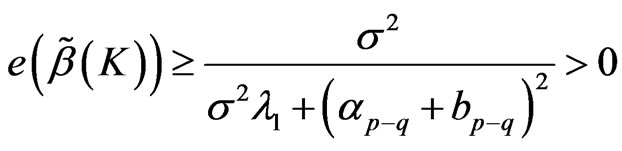 , let
, let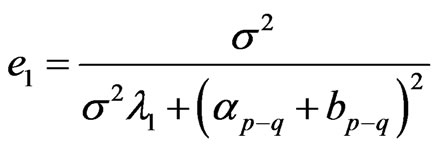 ,
,
then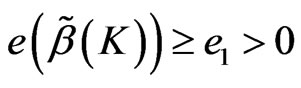 .
.
Theorem 5 In the model (1), assume the non-zero characteristic root  of W are not all equal
of W are not all equal  , for the efficiency lower bound
, for the efficiency lower bound 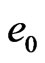 of
of 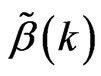 and the efficiency lower bound
and the efficiency lower bound 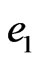 of
of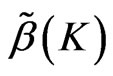 , the relationship of them is
, the relationship of them is .
.
Proof: By theorems 3 and 4, we get 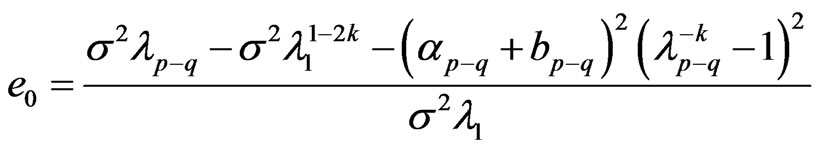 ,
,
 note
note 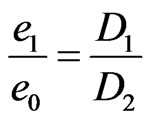 then
then
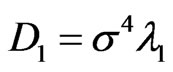 ,
,
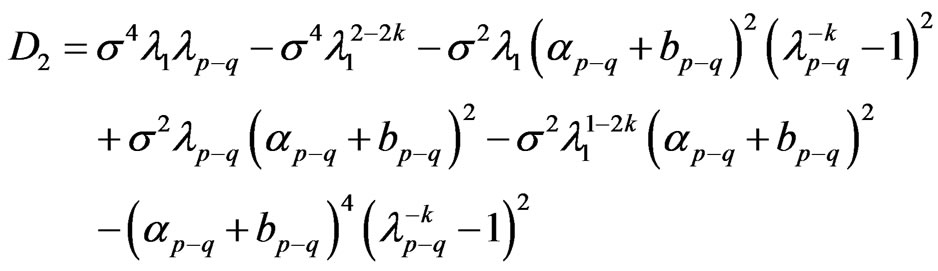
Then
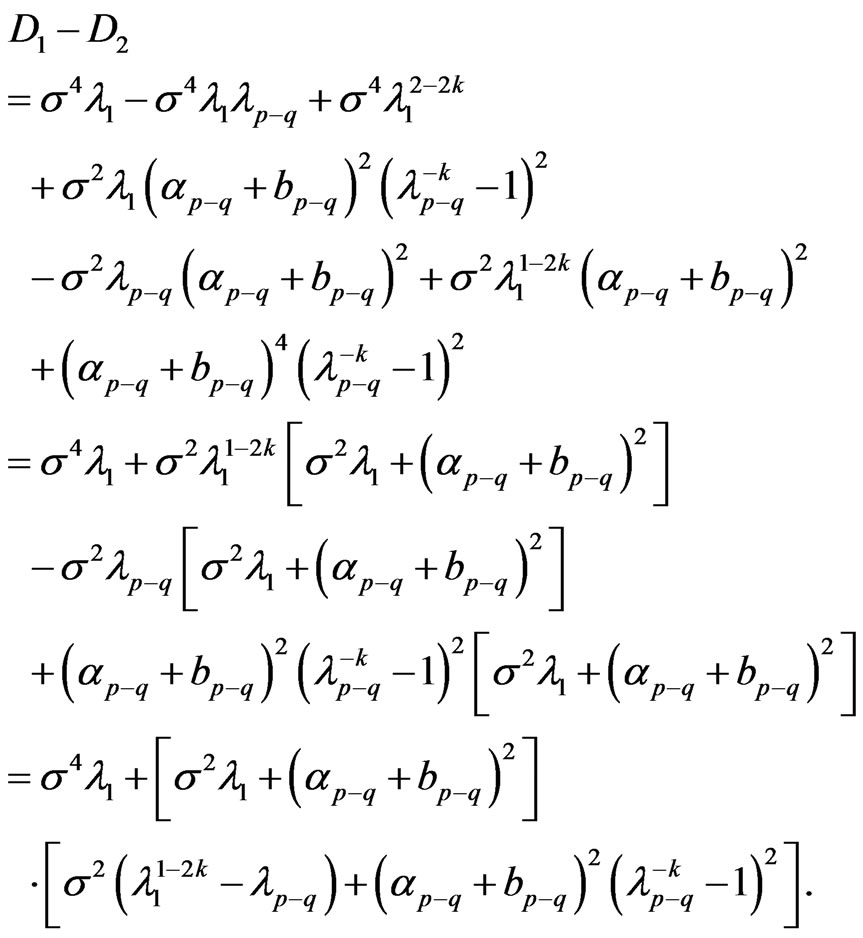
As 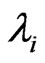 are not all equal
are not all equal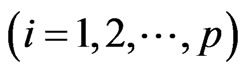 , therefore
, therefore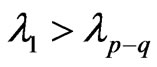 , also
, also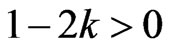 , then
, then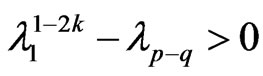 , thus
, thus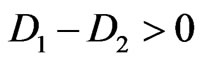 .
.
That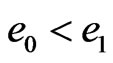 .
.
REFERENCES
- X.-L. Nong and W.-R. Liu, “The Conditional Root Square Estimation of Parameter of Restricted Linear Model,” Journal of Chongqing Normal University (Natural Science Edition), No. 2, 2007, pp. 24-28.
- X.-L. Nong, W.-R. Liu, et al., “The Generalized Conditional Root Squares Estimation of Parameter in Restricted Linear Model,” Journal of Guangxi University of Technology, Vol. 18, No. 3, 2007, pp. 24-27.
- P.-H. Wang, “The Relative Efficiency of the Generalized Ridge Estimation,” Journal of QuanZhou Normal College, Vol. 2, 1998, pp. 13-15.

