Received 18 June 2014; revised 21 July 2014; accepted 1 August 2014

ABSTRACT

The aim of this work is to study the notion of the gradient observability on a subregion 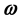of the evolution domain 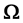for a class of semilinear hyperbolic systems. We show, under some hypothesis, that the gradient reconstruction is achieved following sectorial approach combined with fixed point techniques. The obtained results lead to an algorithm which can be implemented numerically.

Keywords:

Distributed Systems, Hyperbolic Systems, Gradient Reconstruction, Regional Observability, Fixed Point, Sectorial Operator

1. Introduction

The regional observability is one of the most important notions of system theory, and it consists in reconstructing the initials conditions (initial state and initial speed) for hyperbolic systems only in a subregion 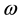of the system evolution domain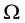. This concept was largely developed (see [1] [2] ) for parabolic systems and for hyperbolic systems (see [3] [4] ). Subsequently, the concept of regional observability was extended to the gradient observability for parabolic systems (see [5] [6] ) and for hyperbolic systems (sees [7] ), which consist in reconstructing directly the gradient of the initial conditions only in a critical subregion interior 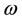without the knowledge of the initial conditions. This concept finds its application in many real world problems.

The aim of this paper is to study the regional gradient observability of an important class of semilinear hyperbolic systems. We will focus our attention on the case where the dynamic of the system is a linear operator and sectorial. This approach was examined for semilinear parabolic systems to reconstruct the initial gradient state ( [8] ) and for semilinear hyperbolic systems to reconstruct the initial state and the initial speed. For observability problem when one is confronted to the question of reconstructing the gradient state and the gradient speed, it is important to take into account the effects of non-linearity. For example, approximate controllability of semilinear system can be obtained when the non-linearity satisfies some conditions (see [9] [10] ), and the used techniques combine a variational approach to controllability problem for linear equation and fixed point method. The techniques are also based on linear infinite dimensional observability theory together with a variety of fixed point theorems.

The plan of the paper is as follows: Section 2 is devoted to the presentation of the problem of regional gradient observability of the considered system. Section 3 concerns the sectorial approach. Numerical approach is developed in the last section.

2. Problem Statement

Let 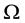be an open bounded subset of.

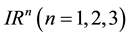For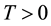, we denote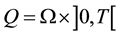, 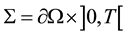and we consider the following semilinear hyperbolic system

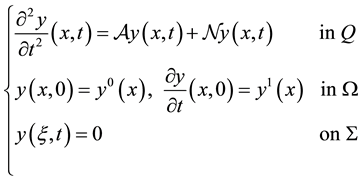(1)

where 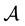is a second order elliptic linear operator, symmetric generating a strongly continuous semigroup

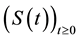and 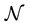is a nonlinear operator assumed to be locally Lipshitzian.

Let 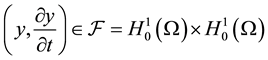denotes the solution of system (1) (see [11] ) and the function of measurements is given by the output function

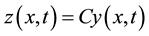(2)

where is a linear operator from to the space, and depends on the number and the nature of the considered sensors.

Let a basis of eigenfunctions of the operator, with Dirichlet conditions and the associated eigenvalues of multiplicity.

For any the semigroup is given by

Without loss of generality we note: and we associate to the system (1) the linear system

(3)

The system (3) admits a unique solution (see [12] ).

Let denote, for all, and.

The system (1) may be written as

(4)

and the system (3) is equivalent to

(5)

Systems (4) and (5) are augmented with the output function

with (6)

The system (1) can be interpreted in the mild sense as follows

(7)

and the output equation can be expressed by

Let be the observation operator defined by

which is linear and bounded with the adjoint.

Consider the operator given by

where

is the adjoint of.

The initial condition and its gradient are assumed to be unknown.

For an open subregion of and of positive Lebesgue measure, let be the restriction operator defined by

where

. (resp.) is the adjoint of (resp.), and we consider the operator

Let be the gradient of the initial condition, we have

(8)

where, and

Definition 1.

The System (3)-(2) is said to be exactly (respectively. weakly) -observable in if

(respectively.

Definition 2.

The semilinear system (1) augmented with output (2) is said to be gradient observable in (-observable in) if we can reconstruct the gradient of its state and the gradient of its speed in a subregion of at any time.

The study of regional gradient observability leads to solving the following problem:

Problem 1.

Given the semilinear system (1) and output (2) on, is it possible to reconstruct which is the gradient of initial state and the gradient of initial speed of (1) in?

Let’s consider and we define, for, the operator by

then we have the following results:

Proposition 1.

If the system (3) is weakly -observable, then the solution of the system (6) is a fixed point of the mapping defined by:

where is the pseudo inverse of the operator and such that

where is the residual part.

Proof

The solution of the system (4) can be expressed by thus, so we have

where is the output function which allows information about the considered system.

Using the second decomposition of initial condition we obtain which is equivalent to.

If the linear part of the system (1) is weakly -observable in, then we have

where is the pseudo inverse of the operator.

Finally, solution of problem of -observability in is a fixed point of the following function: define by:

(9)

Proposition 2.

If is closed in and if the function (9) has a unique fixed point such that

(10)

then is the initial gradient to be observed in of system (4).

Proof

Let a fixed point of equation (9), then

But the operator is the orthogonal projection of in and satisfy

condition (10), then.

Finally

which is the initial gradient to be observed in of system (4).

3. Sectorial Approach

In this section, we study Problem 1 under some supplementary hypothesis on and the nonlinear operator.

With the same notations as in the previous case, we reconsider the semilinear system described by the equations (4) and (6) where one supposed that the operator generates an analytic semigroup in the state space.

Let’s consider such that with is a positive real number and

denotes the real part of spectrum of. Then for, we define the fractional power as a closed operator with domain which is a dense Banach space on endowed with the graph norm

and consider.

We consider Problem 1 in endowed with the norm

(11)

We have

where is a constant. For more details, see ( [2] [6] [13] )

For, assume that

(12)

And the operator is well defined and satisfies the following conditions:

(13)

Those hypothesis are verified by much important class of semi linear hyperbolic systems. For example the equation governing the flow of neutrons in a nuclear reactor

which.

The operators and corresponding are

;

The assumption is satisfied with and.

Various examples are given and discussed in ( [13] [14] ).

We show that exists a set of admissible initial gradient state and admissible initial gradient speed, admissible in the sense that system (3) be weakly -observable.

Let’s consider given by

where is the restriction in and is the residual part in of the initial gradient condition.

We assume that

(14)

then we have the following result.

Proposition 3.

Suppose that system (3) is weakly -observable in, and (12), (13) and (14) satisfied, then the following assertion hold:

・ There exist and such that for all the function has a unique fixed point in the ball solution of the system (4).

・ There exist and such that the mapping f is lipschitzian where

Proof

・ Since, then there exists such that and we have.

Let us consider and in and we have

where

Using Holder’s inequality we take and using (13), we have

On the other hand, we have

but we have

and

and using Holder’s inequality we obtain

then we have

and

or

where

Finally

Let’s consider and , then.

It is sufficient to take and, then for all we have

Let and be the solution of system (4) corresponding respectively to the initial gradient in, we suppose that we have the same residual part, then for we have

but we have

and we deduce that

(15)

Finally is lipschitzian in.

Remark 1.

The given results show that there exists a set of admissible gradient initial state. If the gradient initial state is taken in, with a bounded residual part then the system (4) has only one solution in.

Here we show that if measurements are in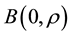, with is suitably chosen then the gradient initial state can be obtained as a solution of a fixed point problem.

Let us consider the mapping

(16)

and assume that.

Then we have the following result.

Proposition 4.

Assume that

(17)

(18)

and if the linear system(3)is weakly -observable in and (13) holds, then there exists and, such that for all, the function (16) admit a unique fixed point in which corresponds to the gradient initial condition observed in. Furthermore, the function

is lipschitzian.

Proof

Let us consider and in, using (11), (13), (15) and (17) we have

or, then there exists such that and we have. Then we obtain.

On the other hand, using the inequality (13), (17) and (18), we have

Let’s consider

In order to have, it suffices to consider.

For, we have

which gives

then

which shows that is Lipschitzian.

4. Numerical Approach

4.1. Numerical Approach

We show the existence of a sequence of the initial gradient state and initial gradient speed which converges respectively to the regional initial gradient states and initial gradient speed to be observed in.

Proposition 5.

We suppose that the hypothesis of Proposition 4 are verified, then for, the sequence of the initial gradient condition defined in by

converges to the regional initial gradient condition (the regional initial gradient state and the regional initial gradient speed) to be observed in, where is the residual part of the initial gradient condition in.

Proof

We have,

or, then there exists ,

Then is a Cauchy sequence on and its convergence.

We consider and with

We have, then

then

which shows that the sequence converges to in.

On the other hand, we have

Then converges to the regional initial gradient to be observed in.

4.2. Algorithm

Now let’s consider the sequence, then we have

and

Thus we obtain the following algorithm:

Algorithm:

1. Given the initial condition, the region, The domain and the function of distribution and the accuracy threshold,.

2. Repeat

a)

b)

c)

Until

3. which corresponds to the initial gradient condition to observed in.

Else and go to step 2.

5. Conclusion

The question of the regional gradient observability for semilinear hyperbolic systems was discussed and solved using sectorial approach, which uses sectorial properties of dynamical operators, the fixed point techniques and the properties of the linear part of the considered system. The obtained results are related to the considered subregion and the sensor location. Many questions remain open, such as the case of the regional boundary gradient observability of semilinear systems using Hilbert Uniqueness Method (HUM) and using the sectorial approach. These questions are still under consideration and the results will appear in a separate paper.

References