Received 29 December 2015; accepted 23 February 2016; published 26 February 2016

ABSTRACT

Among all statements of Second Law, the existence and uniqueness of stable equilibrium, for each given value of energy content and composition of constituents of any system, have been adopted to define thermodynamic entropy by means of the impossibility of Perpetual Motion Machine of the Second Kind (PMM2) which is a consequence of the Second Law. Equality of temperature, chemical potential and pressure in many-particle systems are proved to be necessary conditions for the stable equilibrium. The proofs assume the stable equilibrium and derive, by means of the Highest-Entropy Principle, equality of temperature, chemical potential and pressure as a consequence. A first novelty of the present research is to demonstrate that equality is also a sufficient condition, in addition to necessity, for stable equilibrium implying that stable equilibrium is a condition also necessary, in addition to sufficiency, for equality of temperature potential and pressure addressed to as generalized potential. The second novelty is that the proof of sufficiency of equality, or necessity of stable equilibrium, is achieved by means of a generalization of entropy property, derived from a generalized definition of exergy, both being state and additive properties accounting for heat, mass and work interactions of the system underpinning the definition of Highest-Generalized- Entropy Principle adopted in the proof.

Keywords:

Many-Particle Systems, Stable Equilibrium, Non-Equilibrium, Second Law, Generalized Potential, Generalized Reservoir, Generalized Exergy, Generalized Entropy, Highest-Generalized-Entropy Principle

1. Introduction

The literature reports that Second Law statement can be enunciated in terms of existence and uniqueness of stable equilibrium for a given value of energy content, compatible with a given composition of constituents and compatible with a given set of parameters of any system A. This statement implies that each subsystem of a whole system has to be individually in stable equilibrium and that the composite of all subsystems mutually interacting with each other has to be in stable equilibrium as well. Stable equilibrium is proved to be a sufficient condition for equality of temperature, equality of potential and equality of pressure, or thermodynamic potentials, in many-particle systems interacting with an external reservoir R by heat, mass and work mutual exchange. Considering the inverse logical inference, the sufficiency of stable equilibrium for equality of thermodynamic potentials is equivalent to the necessity of equality of temperature, potential and pressure, inside the system and between system and reservoir, for stable equilibrium of the composite system-reservoir AR. The proof of sufficiency of stable equilibrium, or equality of thermodynamic potentials, is achieved by Gaggioli through the Lowest-Energy Principle [1] and also by Gyftopoulos and Beretta through the Highest-Entropy Principle [2] .

The Second Law implies the definition of thermodynamic entropy property for a composite resulting from a system A and a reservoir R mutually interacting to determine the state of stable equilibrium of the composite AR [2] . The canonical definition of thermodynamic entropy can be proved by means of the concept of Perpetual Motion Machine of the Second Kind (PMM2) in turn representing a consequence to Second Law statement founded on existence and uniqueness of stable equilibrium [2] . The definitions of thermodynamic entropy reported in the literature are based on the temperature as the unique intensive property, or thermodynamic potential, which specifically characterizes heat interactions. At stable equilibrium, temperature has to be equal in all points of space region occupied by a system and the proof is achieved by the Highest-Entropy Principle. Besides, potential and pressure are additional necessary conditions, for stable equilibrium, to equality of temperature, and for potential and pressure necessity too, the proof is based again on the same Highest-Entropy Principle [2] . Thus, the existence and uniqueness of stable equilibrium imply PMM2 used to define entropy expressed by the temperature which, instead, does not represent the unique thermodynamic potential to be equal in the system for stable equilibrium. Therefore, potential and pressure are necessary conditions for stable equilibrium in addition to temperature; however potential and pressure do not appear neither in the canonical expression of thermodynamic entropy, nor in the Highest Entropy Principle. This logical inconsistency represents the outset of this research and its resolution is the objective to be achieved.

2. Assumptions and Method

The present analysis focuses on many-particle systems A constituted by particles interacting each other through inter-particle potential energy, here addressed to as potential, and inter-particle kinetic energy, namely temperature, determined by particles relative position and velocity respectively and constituting the system configuration at any state. The thermodynamic state of A can be global equilibrium or global non-equilibrium [2] -[4] .

The reservoir R consists of an auxiliary system behaving at constant temperature, constant potential 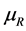and constant pressure while interacting with A and experiencing stable equilibrium states only [5] [6] . R is assumed to be any subsystem or external system, or a combination of the two, not limited to the environment for this reason here defined as generalized reservoir.

The method adopted is based on the canonical expression of entropy property

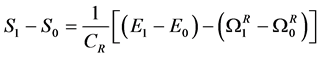
where 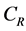is a positive and constant parameter depending on the characteristics of the reservoir only, E is the energy of the system and represents the generalized available energy of the composite AR so that entropy is an inherent property of any system, large or small, valid for equilibrium and non-equilibrium states where the function of reservoir is only auxiliary [2] [3] .

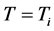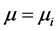The set of necessary conditions for stable equilibrium consisting of equality of temperature, , equality of potential, and equality of pressure, , 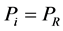where i represents the 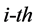subsystem of the whole system, will be accounted for in defining the generalized entropy deduced from generalized exergy property. If reference is made to a generalized reservoir, then the definition of exergy 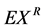results correlated to the generalized available energy which is considered a particular case of generalized adiabatic availability [2] , hence:

(1)

This definition of thermodynamic entropy is underpinned by equal temperature as the sole necessary condition for the stable equilibrium of AR and for this reason is based only on the constant temperature of the reservoir [3] [4] . Instead, the stable equilibrium implies the necessary conditions of equal potential and equal pressure, in addition to equal temperature, of two interacting systems [2] , nevertheless chemical potential and pressure of the reservoir do not appear in the definition of entropy property. To resolve this inconsistency, the definition of entropy will be generalized so that equality of potential and equality of pressure will be accounted for as necessary conditions of stable equilibrium in addition to equality of temperature to account for and in addition to. The definition of generalized entropy will be obtained from the generalized exergy here defined and underpins the statement of the Highest-Generalized-Entropy Principle suitable to infer that equality of temperature, equality of potential and equality of pressure are conditions also sufficient for stable equilibrium, in addition to necessity. The proof accounts for independent thermal, chemical and mechanical contributions to the generalized entropy associated to heat, mass and work interactions respectively.

Finally, the proof of definition of entropy property in which [2] , is based on the concept of Perpetual Motion Machine of the Second Kind (PMM2) representing a consequence of Second Law statement. A specific characterization of PMM2 will be used to demonstrate that is also proportional to or.

3. Necessity and Sufficiency of Temperature Equality

The canonical definition of physical exergy property is based on the amount of heat and work interactions occurring until the system reaches the mutual stable equilibrium with the reservoir. In particular, the (thermal) exergy between two thermodynamic states connected by a process, is

and corresponds to the maximum net useful work, obtained by means of a weight process resulting from the difference of generalized available energy between the (variable) temperature T of system A and the (constant) temperature of a reservoir R.

Physical exergy canonical definition reported in the literature [2] is

where the term constitutes the exergy loss corresponding to the amount of heat released to the reservoir once the equality of temperature, between system and reservoir has been achieved at thermal equilibrium. The term expresses the amount of work released to the reservoir at constant pressure differing from the (variable) pressure P of the system, as the composite system-reservoir AR is not in stable equilibrium even though AR is in a (restricted) thermal stable equilibrium state due to the equality of temperatures.

According to the procedure reported in the literature [2] , thermodynamic (thermal) entropy is defined as

and, taking into account the above mentioned relationship between

(thermal) generalized available energy and (thermal) physical exergy:

(2)

The above equation of entropy is associated to, and is determined by, heat interaction of system A with the reservoir R at temperature and for this very reason is here specified as thermal entropy. This definition of thermal entropy is proved by means of the impossibility of the PMM2 to perform a direct ideal cycle converting a total amount of heat into work with no heat released at lower temperature or, in other terms, without net effects on the external system. Being energy and generalized available energy defined for equilibrium and non-equili- brium states, thermodynamic entropy is valid for any state as well [2] -[4] .

The expression of thermal entropy property depends solely on temperature and does not include pressure despite it appears in the definition of thermal exergy property and despite pressure equality represents a necessary condition of stable equilibrium in addition to temperature equality. Although the equality of temperature is a necessary condition of stable equilibrium derived through the Highest-(Thermal)-Entropy Principle [2] [7] , this condition is not unique. In fact, even when two interacting systems are in thermal stable equilibrium due to equal temperatures, these systems can experience (constraints removed) states of non-equilibrium due to a not null difference of potential and or pressure. Therefore, equality of temperature has to be integrated by equality of potential and equality of pressure between system and reservoir and have to jointly constitute the set of necessary conditions ensured by the stable equilibrium of a system-reservoir composite. Whilst entropy property being defined solely with respect to the constant temperature of the reservoir [2] -[4] , the proof that equal potential and equal pressure are additional necessary conditions for stable equilibrium is founded on the Highest-(Thermal)-Entropy Principle [2] which is correlated to the Lowest-(Thermal)- Energy Principle [1] . The reason is that Second Law states the existence and uniqueness of stable equilibrium for each given value of energy related to entropy which is a consequence of Second Law itself. In fact, the fundamental relation of Stable-Equilibrium-State Principle establishes the relationship between energy and entropy, and in particular, energy depending on temperature, potential and pressure within the system at stable equilibrium as reported by Gyftopoulos and Beretta [2] :

,

and entropy depending on temperature, potential and pressure as well being the inverse equation of the former:

.

However, the Highest-(Thermal)-Entropy Principle couldn’t be able to prove the necessity of equal potential and equal pressure since the canonical definition of (thermal) entropy does not account for the equal potential, and equal pressure, and does not make reference to independent mass interaction or work interaction between system and reservoir. On the other hand, since the proof of necessity of equal temperature does not explicitly refer to the temperature of reservoir (or an intermediate equal temperature at stable equilibrium between system and a subsystem behaving as a reservoir), then entropy used in Highest-(Thermal)-Entropy Principle is intended to be valid also for potential and pressure [2] . Hence, the definition of entropy should require a generalization extended to mass and work interactions in order to account for the independent contributions of chemical entropy and mechanical entropy, in addition to thermal entropy, evaluated with respect to a reservoir at constant potential and constant pressure to validate its applicability to non-equilibrium states caused by potential and pressure non-equality between system and reservoir.

It is noteworthy that the necessity of equal temperatures within the composite AR implies that the assumption of stable equilibrium determines solely equal temperature and not necessarily equal potential and equal pressure which, therefore, do not ensure stable equilibrium itself as, instead, is assumed. Hence, equality of potential and equality of pressure have to become necessary conditions to be satisfied jointly with equality of temperature. Once equal temperature, potential and pressure within AR are assumed as a set of necessary conditions, then this set of conditions has to be proved to be also sufficient. Therefore, these equality conditions have to be necessary and sufficient with the consequence that stable equilibrium has to be sufficient and necessary condition as well. Thus, stable equilibrium is proved to be a necessary condition if it is derived from equality of temperature, equality of potential and equality of pressure, here addressed to as equality of generalized potential, within AR composite. This bi-univocal logical inference represents the objective of this study and will be proved in following sections.

From differential standpoint, if reference is made to the canonical definition of entropy property

the term or constitutes the integrating factor which makes the heat interaction an

exact differential according to Pfaff theorem and Schwarz relation. In fact, considering a process characterized by both heat interaction and work interaction, the Gibbs equation for an ideal gas is which, by virtue of the state equation becomes or, is an exact differential. Instead, δQ and δW are not individually exact differential. Indeed, applying the Schwarz relation to the expression it follows that and thus the Schwarz relation does not hold and δQ is not a state property. As known, multiplying the expression of δQ by the integrating factor then the ratio becomes the definition of thermal entropy which is a state property.

4. Necessity and Sufficiency of Potential Equality

Stable equilibrium is proved to be a sufficient condition for equality of potential between two interacting systems, in addition to equality of temperature and pressure. The proof reported in the literature assumes stable equilibrium, for a given energy content, to derive equality of potential using the Highest-(Thermal)-Entropy Principle where entropy depends solely on [2] . However, potential of the reservoir, and therefore equality of potential, is not accounted for in the definition of entropy property expressed in Equation (2). Since stable equilibrium is achieved once equality of potential is a condition verified in addition to equality of temperature and pressure (restricted stable equilibrium), then entropy equation should include the contribution of chemical entropy, associated to and determined by mass interaction and defined with respect to and the equality of system and reservoir potential, , in addition to the contribution of thermal entropy associated to heat interaction.

A system A with n chemical constituents is considered interacting with a chemical reservoir R assuming restricted stable equilibrium in the composite system-reservoir undergoing processes at equal temperature and pressure but different chemical potential so that mass can flow from system to the reservoir characterized by variable amount of constituents. The maximum net useful work withdrawn from A interacting with R, undergoing a process from initial state 0 to final state 1, until the system-reservoir composite AR reaches the chemical stable equilibrium state, corresponds to the chemical exergy, expressed by the following equation reported by

Kotas [8] : where the superscript “C” stands for “Chemical reservoir” since the

composite of system and reservoir undergoes a “mass interaction” determining a “useful work”. Mass interaction is characteristic of chemical energy transfer and it is moved by the difference of chemical potential between the system and the chemical reservoir. For this reason the expression of chemical exergy reported by Moran and

Sciubba [9] can be expressed as: where represents the chemical potential of the

constituent. In the general case of a mixture consisting of n chemical constituents, according to the defini-

tion [9] : where is the molar fraction of the constituent.

A definition of chemical entropy can be derived from chemical energy and chemical exergy according to the method previously adopted and the general definition of Equation (1). To do so, if the concept of (chemical) generalized available energy is again considered, the formulation of chemical exergy should be translated into which, in case of a chemical reservoir, becomes

. Now that chemical exergy is defined, chemical entropy may be derived

from both chemical energy and (chemical) generalized available energy which depend on mass interaction:

. Assuming that energy and generalized available energy are additive

properties, chemical entropy is an additive property as well and considering that the generalized reservoir allows a correlation between chemical generalized available energy and chemical exergy, then chemical entropy can be formulated as:

(3)

Chemical entropy is associated to and is determined by mass interaction between A and R at constant potential. This definition is valid for non-equilibrium, in addition to stable equilibrium, between system and chemical reservoir since it is derived through the same procedure adopted for equation of thermal entropy valid in turn for non-equilibrium states [2] . Nevertheless, it follows from the Second Law stated, in this case, as existence and uniqueness of chemical stable equilibrium since thermal and mechanical stable equilibrium are posited as restricted stable equilibrium.

Chemical entropy definition can be proved by means of PMM2. One could imagine a machine with a two- phase fluid operating at constant temperature between two different and constant pressures. The impossibility of PMM2 does not allow to withdrawn work interaction without net changes in the environment here constituted by the reservoir interacting with the system by mass transport. The proof, already provided by Gyftopoulos and Beretta to define the thermodynamic entropy, is general and no specific mention is made to its physical meaning, or to specific assumptions relating to the characteristics of the system, the number and type of particles, the type of potential as well as to the thermodynamic state. This is the rationale behind the generality of the theorems and proofs which, therefore, may be considered still valid also for chemical entropy here defined. This results from the fact that chemical entropy is an inherent property of any system, in any state. Therefore, the chemical entropy can be adopted to state the Highest-Chemical-Entropy Principle which can be assumed as complementary to the Lowest-Chemical-Energy Principle.

Necessity of equality of chemical potential for stable equilibrium can be proved by the Highest-Chemical- Entropy Principle which can also be adopted for the proof of sufficiency to infer chemical stable equilibrium from potential equality. This bi-directional logical implication can be worded as the necessity and sufficiency of chemical potential equality between the system and chemical reservoir, given the equality of temperature and pressure of the system-reservoir composite (restricted stable equilibrium).

Also in this case, from differential standpoint, the chemical entropy as for Equation (3) depends on the potential of reservoir and is formally analogous to the thermal entropy as for Equation (2) depending on the temperature of reservoit. The term in Equation (3) corresponds to the term in Equation (2) and, in this analogy, Chemical-Mechanical State Equation for an ideal multi-particle system results from the equivalence between inter-particle kinetic energy, associated to the temperature depending on particles relative velocity, and inter-particle potential energy, associated to the density depending on particles relative position, and can be expressed as. This state equation is suitable to prove that the term constitutes the integrating factor which makes the mass interaction an exact differential according to Pfaff theorem so that chemical

entropy is a state property. Considering the Pfaff theorem for an adiabatic process of a closed

system, Gibbs equation is where represents the specific mass (or the amount of mass corresponding to an increase of potential equal to one unit). That said, Gibbs equation can be written as

or representing the Pfaff equation. Applying Schwarz relation to Pfaff

theorem, it follows that and so that it is an exact differential.

In case of adiabatic process of an open system undergoing mass interaction, Gibbs equation assumes the form

. The first consequence is that for which Schwarz relation is not valid any-

more since while. The second consequence is that

for which again Schwarz relation is not valid anymore since while.

Assuming that behaves as an integrating factor, then which fulfils the

Schwarz condition being and therefore representing the definition of che- mical entropy as a state property.

5. Necessity and Sufficiency of Pressure Equality

Stable equilibrium is proved to be a sufficient condition also for equality of pressure within the AR composite in addition to equal temperature and equal potential [2] . The proof assumes stable equilibrium between two interacting systems to derive equality of pressure using the Highest-(Thermal)-Entropy Principle. However, also in this case, pressure and therefore equality of pressure between system and reservoir is not accounted for in the definition of entropy property which instead should include the mechanical entropy associated to and determined by thermodynamic work interaction, in addition to thermal entropy and chemical entropy contributions. A definition of mechanical entropy is here proposed analyzing the work interactions between system and a mechanical reservoir behaving at constant pressure.

The weight process represents the experimental measure of the maximum net useful work interaction

withdrawn from a system A releasing a corresponding minimum non-useful heat to a

(thermal) reservoir at constant temperature [2] -[4] according to the definition of generalized available energy and thermal exergy. The inverse (and reversible) process requires the weight process to represent the minimum net useful work released to A while extracting a corresponding maximum non-useful heat from. On the other hand, in addition to the maximum net useful work, the concept of available energy [1] addresses to

the maximum net useful heat associated to the minimum net useful work released to

the mechanical reservoir at constant pressure. This symmetric process underpins the definition of mechanical exergy [10] . In fact, in this case, the input work occurs through the interaction of system A with mechanical reservoir. As work interaction released to the mechanical reservoir is non-useful work, then it is no longer useful since it constitutes the non-convertible contribution of input work interaction. There-

fore, mechanical exergy property accounts for the maximum net useful heat withdrawn from the

system A releasing the minimum non-useful work to the mechanical reservoir. In this symmetric process, system A interacts with a mechanical reservoir behaving at constant pressure therefore the symbol is adopted with the superscript “M” standing for “Mechanical reservoir”:

(4a)

and considering again the meaning of generalized reservoir, then:

(4b)

This relation expresses the mechanical exergy corresponding to the amount of generalized mechanical availa-

ble energy of system A converted into heat interaction at variable temperature which is different

with respect to the constant temperature of thermal reservoir. Indeed, is determined by

the minimum amount of work interaction released to the mechanical reservoir along the isothermal

process where the heat interaction is withdrawn at T_R from the thermal reservoir to be converted into.

In fact, work interaction along the isothermal expansion process, could not be considered useful because it has to be entirely converted into heat by means of an inverse Joule cycle releasing heat (non-useful) to the thermal reservoir and non-useful work to the mechanical reservoir at a lower and constant pressure.

Thus, the maximum net useful heat results from the conversion process in which the input work

rises up to higher temperature the heat input withdrawn from the thermal reservoir constant temperature T_R while releasing, along the isothermal process at constant T_R, the minimum amount of non-useful work interaction expressed as follows [11] :

(5)

The term equals the (theoretically minimum) amount of work released to the mechanical reservoir and equals the low temperature heat, withdrawn from the thermal re-

servoir, converted into high temperature heat.

The definition of mechanical exergy, formulated by Equations (4a) and (4b), constitutes the basis to derive the expression of mechanical entropy using the same procedure adopted for thermal entropy and chemical entropy:

, and taking into account the mentioned relationship between me-

chanical generalized available energy and mechanical exergy:

(6)

The former Equation (5), substituted in the latter Equation (6), implies the expression of mechanical entropy [11] :

(7)

This expression is a consequence of the Second Law and the stable equilibrium state in a system-reservoir composite AR.

The proof of definition of entropy provided by Gyftopoulos and Beretta [2] may be used―mutatis mutandis―as a proof of mechanical entropy as well. In fact, the Second Law statement implies the impossibility of a PMM2 performing, in the case of mechanical entropy, an inverse cycle (instead of direct cycle) so that it may be expressed as the impossibility for mechanical energy to be transferred from a mechanical reservoir at lower pressure to a system at higher pressure P without the contribution of heat interaction. The impossibility of inverse PMM2 expresses the impossibility of any system to undergo a cyclic process that produces no external effect except the heat interaction and the change of another system from an initial state of stable equilibrium to a final state of non-equilibrium. Clearly both process have to be cyclic and therefore for both it is impossible to convert the entire amount of energy content transferred to the other one.

The definition of mechanical entropy can be used to state the Highest-Mechanical-Entropy Principle applicable to those processes causing changes in volume of the system. As regard pressure equality between system and mechanical reservoir, this condition can be proved, using the Highest-Mechanical-Entropy Principle, to be a necessary condition of mutual stable equilibrium between system and reservoir that needs to be complied, in addition to equality of temperature and equality of potential, to ensure the equilibrium state of the composite system-reservoir extending to pressure the stable equilibrium restricted to temperature and potential. On the other hand, the same Highest-Mechanical-Entropy Principle can be adopted to prove the sufficiency of pressure equality or, in different terms, to prove stable equilibrium from pressure equality within system-reservoir composite. This procedure is reported in next sections.

As far as the Pfaff theorem and Schwarz relation are concerned, is not an exact differential. Indeed thus and. In this case, if the former equation is mul-

tiplied by the integrating factor then it results that

from which and so that is an exact differential for and represents the mechanical entropy as a state property according to Pfaff theorem.

Although readers could consider the following clarification as obvious, it is worthy further underline that the concept of mechanical entropy here defined is correlated to the thermodynamic work only and has nothing to do with mechanical work. To better clarify, mechanical work is intended as the transfer work done by an external system behaving as an incompressible fluid, such as a liquid interacting with an hydraulic turbine whereas the thermodynamic work consists of the expansion work done by the internal system behaving as a compressible fluid, such as a vapor (steam) or a gas interacting with the expander of a gas turbine or with a cylinder-piston device.

6. Generalized Entropy Derived from Generalized Exergy

The definition of exergy is characterized by the property of additivity because it is defined with respect to an internal subsystem of the whole system [1] , or to an external reference system behaving as a reservoir [2] [3] . The definition of a generalized reservoir, characterized by constant temperature, constant chemical potential and constant pressure, implies the property of additivity of the components, thermal, chemical and mechanical, constituting the generalized exergy so that the sum of all contributions can be expressed as follows:

(8)

Generalized exergy can be regarded as the sum of generalized physical exergy, resulting from the sum of thermal exergy and mechanical exergy [10] , and generalized chemical exergy, resulting from the sum of chemical exergy and mechanical exergy [11] . An expression of the first one can be provided through two different procedures based on non-cyclic processes [10] and on cyclic processes, in particular the Carnot and Joule cycles [12] [13] .

Likewise, the additivity of the entropy property is proved considering the additivity of energy and generalized exergy from which it is defined. On the basis of the additivity of the entropy property, the generalized entropy results as the sum of entropy contributions, each derived from the corresponding exergy contribution, related to the generalized potential constituted by the set of temperature, chemical potential and pressure of the system. Therefore, generalized entropy can be expressed as follows:

(9)

Generalized entropy is derivable from generalized exergy for any state of the system, equilibrium or non- equilibrium with respect to generalized reservoir having auxiliary function only. For this reason, as the method expressed in Equation (1) is adopted, it depends on the properties of both system, namely system’s generalized potential and reservoir’s generalized potential. This condition implies equality of temperature, potential and pressure between system and reservoir which become a set of necessary conditions for the stable equilibrium state of the system-reservoir composite. The generalized entropy can be defined as an extensive and additive property resulting from the sum of entropy contributions (reversibility) and generations (irreversibility) associated to each kind of energy content (thermal, chemical, mechanical) transferred between two subsystems of a whole system by means of the related heat, mass or work interaction respectively. Although entropy property depends on temperature, potential and pressure (or generalized potential) by virtue of the Stable-Equilibrium-State Principle, its contributions are related to, and dependent on, each one of the specific interaction constituting the transfer of each specific energy namely thermal energy, chemical energy and pressure energy. The physical meaning of generalized entropy is that each form of energy is characterized by its own specific form of entropy property expressing the contribution or generation associated to energy transfer and respective heat, mass or work interaction.

Going back to Pfaff theorem demonstrated for each one of entropy components, or are not individually exact differentials if occurring simultaneously (in parallel), however they become exact differentials if occurring sequentially (in series). As well, or are not individually exact differentials if occurring simultaneously (in parallel), as well they become exact differentials if occurring sequentially (in series).

Although entropy property depends on temperature, potential and pressure (or generalized potential) by virtue of the Stable-Equilibrium-State Principle, its contributions are related to and dependent on each one of the specific interaction constituting the transfer of each specific energy, namely thermal energy, chemical energy and pressure energy, constituting the internal energy of whole system.

7. Highest-Generalized-Entropy Principle

The generalized statement of Highest-Entropy Principle is based on the definition of generalized entropy property. Hence, it is possible to state that the Highest-Generalized-Entropy Principle results from the contribution of thermal entropy, chemical entropy and mechanical entropy as well as the property of additivity. Then the Highest-Generalized-Entropy Principle is consistent with the Highest-Thermal-Entropy Principle, Highest-Chemical- Entropy Principle and Highest-Mechanical-Entropy Principle proved for each entropy property related to heat, mass and work interaction between system and reservoir. Therefore, making reference to the statement formulated by Gyftopoulos and Beretta [2] , the Highest-Generalized-Entropy Principle implies that among all states of a system characterized by given value of energy, number of constituents and parameters such as volume, there exist a unique stable equilibrium, according to Second Law statement here addressed to, and generalized entropy of this state is larger than the generalized entropy of any other state with the same value of energy, number of constituents and parameters.

On the other hand, if all states with same value of generalized entropy are considered, and assuming the Stable-Equilibrium-State Principle as the relationship between energy and entropy as reported in previous Section 3, one can infer the Lowest-Generalized-Energy Principle implying that among all states of a system characterized by given value of entropy, number of constituents and parameters, the generalized energy of the unique stable equilibrium state is lower than the generalized energy of any other state with the same value of generalized entropy, number of constituents and parameters.

8. Necessity and Sufficiency of Generalized Potential Equality

The present section describes the proof that generalized potential equality is a condition necessary and sufficient for stable equilibrium (or that stable equilibrium is a condition sufficient and necessary for generalized potential equality). This proof is included in a paper already published by the author [14] nevertheless is here again reported for sake of completeness and consistency as well as to better clarify the rationale behind the generalization of properties and principles here proposed.

According to the proof theory, deriving a thesis from a hypothesis implies the logical proof of hypothesis sufficiency and, vice versa, deriving the hypothesis from the thesis implies the logical proof of hypothesis necessity. The opposite is valid if thesis is replaced by hypothesis or, consistently, if hypothesis is replaced by thesis. The proof that equality of temperatures, potentials and pressures within the whole composite system-reservoir are necessary condition of stable equilibrium, hence “Equilibrium => Equality”, is described by Gyftopoulos and Beretta [2] who adopt the Highest-Entropy Principle to prove that temperature-potential-pressure equality is the consequence of subsystems individual-and-interacting stable equilibrium. With an opposite logical inference, the proof that individual-and-interacting stable equilibrium is inferred from temperature-potential-pressure equality is achieved by Gaggioli by adopting the Lowest-Energy Principle [1] . Therefore, in both cases, stable equilibrium is a sufficient condition for equality, hence, once again, “Equilibrium => Equality”. As sufficiency of equilibrium (or necessity of equality) is the sole condition established and proved and, on the other hand, the necessity of stable equilibrium (or sufficiency of equality) is not proved, then the system-reservoir composite can experience equality of temperature, potential and pressure while the composite itself is not in a stable equilibrium state since the equilibrium is not necessary as well (or equality is not sufficient as well) in contradiction to the assumed stable equilibrium. To resolve this contradiction, stable equilibrium has to be sufficient and necessary condition for equality of generalized potential or, vice versa, equality of generalized potential has to be necessary and sufficient condition for stable equilibrium. Reference can be made to the thermal, chemical, mechanical contributions of entropy, which is an additive property, so that the sum of these contributions constitutes generalized entropy which is the base of Highest-Generalized-Entropy Principle. To prove the necessity and sufficiency, without disproving the proofs already provided in the literature, one has to demonstrate that equality (or equilibrium) is necessary and sufficient conditions, thus Gaggioli’s statement is also necessary and Gyftopoulos and Beretta’s statement is also sufficient, both implying that the inference “Equality => Equilibrium” is complementary to the inference “Equilibrium => Equality” so that both equilibrium and equality are necessary and sufficient conditions for each other. In different terms, stable equilibrium is true if and only if generalized potential equality is true and vice versa generalized potential equality is true if and only if stable equilibrium is true. Figure 1 represents the hierarchical structure of the statement of necessity and sufficiency conditions.

Thus, Gaggioli adopts the Lowest-Energy Principle and Gyftopoulos and Beretta adopt the Highest-Entropy Principle, and since entropy depends on the difference between energy and generalized available energy which express the First Law and Second Law respectively, then entropy remains the suitable quantity to attain the proofs of both sufficiency and necessity. Therefore entropy property should account for equality of potential and equality of pressure, in addition to equality of temperature, in order to constitute the procedure for such a proof. First and Second principles are mutually correlated to each other: Lowest-Energy Principle ó Highest-Entropy Principle. In fact, the Stable-Equilibrium-State Principle establishes the mathematical relationship among all system properties at stable equilibrium. This relationship also exists between the Lowest-Energy Principle and the Highest-Entropy Principle which are intrinsic to the Stable-Equili- brium-State Principle as stated by the above fundamental relations [2] .

The proof of the necessity of stable equilibrium (or the sufficiency of generalized potential equality) consists of deriving stable equilibrium from equality and may be established through the “reductio ad absurdum” assuming that temperature, potential and pressure of system and reservoir are equal while the system-reservoir composite is not in stable equilibrium. Indeed, this condition is admitted by the sufficiency of stable equilibrium as the only

condition which does not “necessarily” imply that stable equilibrium is a consequence of equality of temperature, potential and pressure in the system-reservoir composite so that the equality may be compatible with non-equi- librium. This equality of generalized potential would thus be able to move the system into a non-equilibrium state without undergoing any net change of the environment, or, would be able to generate a weight process by means of a PMM2 which is impossible according to the Second Law statement based on stable equilibrium as assumed. The consequence is that equality must imply stable equilibrium, that is, equality must be a sufficient condition for stable equilibrium (or stable equilibrium must be a necessary condition for equality). The proof of this sufficiency can be based on the Highest-Generalized-Entropy Principle where generalized entropy depends on thermal, chemical and mechanical contributions associated to heat, mass and work interactions between system and reservoir. Indeed, entropy property depends on temperature, potential and pressure, however this relationship does not “suffice” to prove stable equilibrium. For instance, adiabatic reversible process, namely isoentropic, causes changes in pressure as well as in temperature but equality of temperature does not in turn imply equality of pressure between system and reservoir. Instead, equality of temperature, potential and pressure associated to heat, mass and work interactions respectively, each individually identified as an additive contribution, ensures stable equilibrium. Adopting once again the paradigm of “reductio ad absurdum”, if equality of generalized potential is not associated to stable equilibrium, then the system can undergo a process due to whatever interaction, bringing it to stable equilibrium with an increase of entropy due to even one type of interaction moved by not equal potential that is impossible as equality is an assumption and being stable equilibrium associated to the highest generalized entropy. Having assumed the equality of generalized potential between system and reservoir, then generalized entropy has to assume the highest value with respect to any other state with non-null difference of temperature, potential and pressure. Therefore, each thermal, chemical and mechanical contribution of generalized entropy, has to be individually the highest. To do so, each individual heat, mass or work interaction, determined by the difference of temperature, potential and pressure respectively, has to be able to bring the system itself to the stable equilibrium state.

Finally, on the basis of the bi-univocal logical inference between stable equilibrium and generalized potential equality, and also considering the validity of Stable-Equilibrium-State Principle which correlates stable equilibrium with all properties characterizing the system in each thermodynamic state [2] , the Second Law statement can be enunciated in terms of existence and uniqueness of generalized potential equality state for each given value of energy content compatible with a given composition of constituents and compatible with a given set of parameters of any system. This statement can be extended to and remains valid also for neutral equilibrium [6] .

9. Conclusions and Future Developments

The result of the present study is twofold. Firstly, it consists of a proposal to encompass the Second Law statement by a bi-univocal logical inference between stable equilibrium, assumed as a hypothesis, and generalized potential equality derived as the thesis of a theorem of necessity and sufficiency of stable equilibrium for generalized potential equality in many-particle systems. The second result is that the proof is achieved by means of the definition of Highest-Generalized-Entropy Principle in which the generalized entropy is derived from generalized exergy property.

A consequence emerging from the generalized definition of entropy is that chemical entropy is an intrinsic and independent property of any system in any state and represents additional contribution, with respect to thermal entropy, determined by potential of the system itself characterized by its atomic and molecular configuration, regardless of the content of thermal entropy. Moreover, chemical entropy characterizes mass interactions of a system with a reservoir even in case no heat interactions are occurring while mass is entering or leaving the system. On the other hand, work interaction, representing the mechanical exergy, can also be correlated to the chemical exergy associated to an amount of mass interaction released to the system. As far as chemical entropy is concerned, future developments may be envisaged for atomic and molecular systems undergoing non-equili- brium phenomena determining specific geometrical configurations within the systems. In particular, Entropy Generation Minimization (EGM) methodology [15] -[17] can include the chemical entropy to provide a system’s evolution schema suitable to describe organized structures and their self-assembling and self-organizing processes especially in living systems at molecular and cellular level [18] -[21] . The definition of generalized entropy can be also extended to Quantum Physics domain to account for the contribution of quantum entropy [22] within the framework of Unified Quantum Theory of Mechanics and Thermodynamics.

Future developments may concern further discussions about generalized entropy, characterizing heat, mass and work interactions depending on temperature, potential and pressure here restricted to many-particle systems. An extension of this generalized paradigm to definitions, properties and theorems relating to few-particle systems and non-equilibrium states will be based on, and account for, recent treatments of thermodynamic entropy property [23] [24] . This recent rigorous and formalized framework of definitions and theorems does not need the concept of reservoir to define thermodynamic entropy for each given value of energy content of the system which depends solely on the temperature. The extension to few-particle systems in non-equilibrium states would involve potential and pressure of the systems, in addition to temperature, aimed at generalizing the definition of thermodynamic entropy to all kinds and forms of potential characterizing matter at molecular, atomic and sub- nuclear level.

Cite this paper

PierfrancescoPalazzo, (2016) A Generalized Statement of Highest-Entropy Principle for Stable Equilibrium and Non-Equilibrium in Many-Particle Systems. Journal of Modern Physics,07,344-357. doi: 10.4236/jmp.2016.73035

References

Nomenclature

: system

: system-reservoir composite

: energy, J

: exergy, J

: mass interaction, J

: chemical constituent, mol

: pressure, Pa

: heat interaction, J

: reservoir

: universal gas constant, J/mol×K

: entropy, J/K

: temperature, K

: internal energy, J

: volume, cubic m

: work interaction, J

: mole

Greek Symbols

: chemical potential, mol×K

: adiabatic availability, J

: available energy, J

Subscripts and Superscripts

: composite system-reservoir

: chemical

: generalized

: irreversible

: mechanical

maximum

: minimum

: net

: reservoir

: reversible

: thermal

: initial state

: final state

: outward interaction flow

: inward interaction flow