Journal of Modern Physics
Vol.06 No.14(2015), Article ID:61306,4 pages
10.4236/jmp.2015.614213
The Masses of 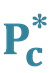 (4380) and
(4380) and 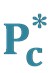 (4450) as Di-Hadronic States
(4450) as Di-Hadronic States
Rismita Ghosh1, Aparajita Bhattacharya1, Ballari Chalrabarti2
1Department of Physics, Jadavpur University, Kolkata, India
2Department of Physics, Jogamaya Devi College, Kolkata, India

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).



Received 7 October 2015; accepted 17 November 2015; published 20 November 2015
ABSTRACT
The masses of the recently reported by LHCb two pentaquark charmonium states 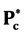 (4380) and
(4380) and 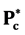 (4450) which are suggested to possess pentaquark configuration (
(4450) which are suggested to possess pentaquark configuration (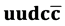 ) have been estimated considering a di-hadronic state consisting of a meson c and a baryon (uud). The binding energies of the states have been estimated with a van der Walls type of molecular interaction between the hadrons. A spin interaction has also been considered. Masses of these two states are well reproduced with the aforesaid molecular interaction which indicates that the multiquarks
) have been estimated considering a di-hadronic state consisting of a meson c and a baryon (uud). The binding energies of the states have been estimated with a van der Walls type of molecular interaction between the hadrons. A spin interaction has also been considered. Masses of these two states are well reproduced with the aforesaid molecular interaction which indicates that the multiquarks 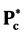 (4380) and
(4380) and  (4450) can be well described as meson-baryon bound states.
(4450) can be well described as meson-baryon bound states.
Keywords:
Pentaquark, Di-Hadronic Molecule, Molecular Interaction

1. Introduction
The existence of pentaquark charmonium states with the decay of 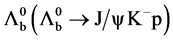 has been reported by LHCb [1] recently. The intermediate states have been identified as
has been reported by LHCb [1] recently. The intermediate states have been identified as 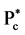 (4380) and
(4380) and 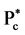 (4450). The states are
(4450). The states are
identified as sum of two up quarks, one down quark, one charm quark and one anti-charm quark with spin 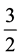 and
and 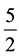 respectively. The identification of these pentaquark states is exciting and will give new impetus to the
respectively. The identification of these pentaquark states is exciting and will give new impetus to the
study of the properties and dynamics of multiquark states [2] . The exotics remain less known and less understood compared to the properties of mesons 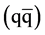 and baryons (qqq) which are well studied both in theory and experiment. The properties and dynamics of exotic states like tetraquark, pentaquark, hexaquark states are yet to be studied and it is well understood that they cannot be described in the framework of conventional quark model. A number of models like the quark model [3] [4] , bag model [5] [6] , and non-relativistic potential models [7] [8] have been used to study the multiquark systems. The description of the multiquark states as di-hadronic states considering them as a bound state of a meson and a baryon is one of the useful candidates for studying the properties of such systems.
and baryons (qqq) which are well studied both in theory and experiment. The properties and dynamics of exotic states like tetraquark, pentaquark, hexaquark states are yet to be studied and it is well understood that they cannot be described in the framework of conventional quark model. A number of models like the quark model [3] [4] , bag model [5] [6] , and non-relativistic potential models [7] [8] have been used to study the multiquark systems. The description of the multiquark states as di-hadronic states considering them as a bound state of a meson and a baryon is one of the useful candidates for studying the properties of such systems.
2. Method
In the present work pentaquark states  (4380) and
(4380) and  (4450) are described as di-hadronic molecules consisting of a meson and a baryon assuming a van der Waals type of molecular interaction acting between the con-
(4450) are described as di-hadronic molecules consisting of a meson and a baryon assuming a van der Waals type of molecular interaction acting between the con-
stituent hadrons [9] [10] . 





has also been considered. Masses of 

Assuming the pentaquark states as meson-baryon system the mass formula for the low-lying di-hadronic molecule runs as:

where M1, M2 represent the masses of the constituent hadrons respectively, EBE represents the binding energy of the di-hadronic system and ESD represents the spin-dependent term.
The binding energy can be expressed as:

where r is the radius parameter of the di-hadronic molecule and V(r) is the di-hadronic molecular potential which is expressed as [9] [10] :

where kmol [9] [10] is the residual strength of the strong interaction molecular coupling and C is the effective colour screening of the confined gluons. It may be mentioned that the residual interaction of the confined gluon is considered similar to van der Waals interaction and is assumed to be due to asymptotic expression (r12 → ∞) of the residual confined one-gluon exchange interaction with strength kmol [9] [10] .
Ψ(r) is the wave function of the di-hadronic state. To estimate EBE we have used the wave functions for the ground state of the hadronic molecule from statistical model which runs as: [11] [12]


corresponding to the linear type of background potential and harmonic type of background potential respectively [11] [12] . r12 is the radius of the hadronic molecule and 


where

The spin hyperfine interaction can be expressed as [20] :

where M1 and M2 are the masses of the constituent hadrons in the di-hadronic molecule, αs is the strong interaction constant, S1 and S2 are the spins of the hadrons involved, 


3. Discussions
In the present work we have estimated masses of particles 



ing them as di-hadronic (meson-baryon) molecules. The masses have been obtained as 4171 MeV and 4492 MeV for 



that the pentaquarks 


Waals type of interaction between them. It is also pertinent to point out that the statistical model wave function is also very successful in describing the hadrons. The pentaquark state is one of the leading candidates for the study of the multiquark state. The description of pentaquark as diquark-diquark-antiquark state has been done by a number of authors [3] [4] . It may be mentioned that recently some predictions of diquark model for hidden charm pentaquarks 

allowed decay channels is given by
Table 1. Binding energies and masses of pentaquark charmonium states as meson-baryon states.
Acknowledgements
Authors are thankful to University Grants Commission, New Delhi, India for their financial supports.
Cite this paper
Rismita Ghosh,Aparajita Bhattacharya,Ballari Chalrabarti, (2015) The Masses of Pc* (4380) and Pc* (4450) as Di-Hadronic States. Journal of Modern Physics,06,2070-2073. doi: 10.4236/jmp.2015.614213
References
- 1. Aaij, R., et al. (LHCb Collaboration) (2015) Physical Review Letters, 115, Article ID: 072001(50).
- 2. Gell-Mann, M. (1964) Physics Letters, 8, 214-215.
http://dx.doi.org/10.1016/S0031-9163(64)92001-3 - 3. Jaffe, R.L., et al. (2003) Physical Review Letters, 91, Article ID: 232003(1-4).
- 4. Karlinar, M., et al. (2003) Physics Letters B, 575, 249-255.
http://dx.doi.org/10.1016/j.physletb.2003.09.062 - 5. Jaffe, R.L. (1977) Physical Review D, 15, 281-289.
http://dx.doi.org/10.1103/PhysRevD.15.281 - 6. Strottman, D. (1979) Physical Review D, 20, 748-767.
http://dx.doi.org/10.1103/PhysRevD.20.748 - 7. Barnes, T., et al. (1987) Physical Review Letters B, 183, 210.
http://dx.doi.org/10.1016/0370-2693(87)90440-0 - 8. Weinstein, J., et al. (1983) Physical Review D, 27, 588.
http://dx.doi.org/10.1103/PhysRevD.27.588 - 9. Vinodkumar, P.C., et al. (1992) Pramana-Journal of Physics, 39, 47-70.
- 10. Vinodkumar, P.C., et al.(2003) DAE-BRNS Symposium on Nuclear Physics, 46B, 334.
- 11. Bhattacharya, A., et al. (1998) European Physical Journal C, 2, 671-673.
- 12. Bhattacharya, A., et al. (2005) Nuclear Physics (Proceedings Supplements), B142, 13.
http://dx.doi.org/10.1016/j.nuclphysbps.2005.01.002 - 13. Rai, A.K., et al. (2006) Indian Journal of Physics, 80, 387-392.
- 14. Chakrabarti, B., et al. (2009) Physica Scripta, 79, Article ID: 025103.
http://dx.doi.org/10.1088/0031-8949/79/02/025103 - 15. Mohr, P.J., et al. (2011) The 2010 CODATA Recommended Values of the Fundamental Physical Constants. National Institute of Standards and Technology, Gaithersburg.
- 16. Alexandrou, C., et al. (2007) PoSLAT2007, 149.
- 17. Banerjee, S.N., et al. (1987) International Journal of Modern Physics A, 2, 1829.
http://dx.doi.org/10.1142/S0217751X87000958 - 18. Bhattacharya, A., et al. (1988) Canadian Journal of Physics, 66, 749-751.
http://dx.doi.org/10.1139/p88-123 - 19. Hong, C., et al. (2001) Chinese Physics Letters, 18, 1558.
http://dx.doi.org/10.1088/0256-307X/18/12/305 - 20. Rai, A.K., et al. (2007) Nuclear Physics A, 782, 406-409.
http://dx.doi.org/10.1016/j.nuclphysa.2006.10.023 - 21. Lucha, W., et al. (1991) Physics Report, 200, 168.
http://dx.doi.org/10.1016/0370-1573(91)90001-3 - 22. Beringer, J., et al. (Particle Data Group) (2012) Physical Review D, 86, Article ID: 010001.
http://dx.doi.org/10.1103/PhysRevD.86.010001 - 23. Li, G.N., et al. (2015) arXiv:1507.08252v2 [hep-ph].



