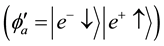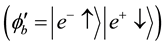Journal of Modern Physics
Vol.06 No.07(2015), Article ID:57671,10 pages
10.4236/jmp.2015.67098
Magnetic Moment of Photon
Ziya Saglam1, Gokhan Sahin2,3
1Department of Physics, Aksaray University, Aksaray, Turkey
2Department Electrical and Computer Engineering, Miami University, Oxford, OH, USA
3Departamento de Electrónica, Telecomunicações e Informática (DETI), Instituto de Telecomunicacoes, University of Aveiro, Aveiro, Portugal
Email: zsaglam@aksaray.edu.tr, sahing@muohio.edu
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 27 April 2015; accepted 27 June 2015; published 30 June 2015
ABSTRACT
We have calculated the intrinsic magnetic moment of a photon through the intrinsic magnetic moment of a gamma photon created as a result of the electron-positron annihilation with the angular frequency w. We show that a photon propagating in z direction with an angular frequency w carries a magnetic moment of mz = ±(ec/w) along the propagation direction. Here, the (+) and (−) signs stand for the right hand and left circular helicity respectively. Because of these two symmetric values of the magnetic moment, we expect a splitting of the photon beam into two symmetric subbeams in a Stern-Gerlach experiment. The splitting is expected to be more prominent for low energy photons. We believe that the present result will be helpful for understanding the recent attempts on the Stern-Gerlach experiment with slow light and the behavior of the dark polaritons and also the atomic spinor polaritons.
Keywords:
Magnetic Moment, Quantum Flux, Gamma Photons, Canonical Angular Momentum

1. Introduction
In an earlier study [1] , we calculated the intrinsic quantum flux of a photon through the intrinsic quantum flux of the gamma photons created as a result of the electron-positron ( -
- ) annihilation. By using the flux conservation rule, which is an element of the conservation of the canonical angular momentum, we find that each gamma photon carries a magnetic flux quantum of
) annihilation. By using the flux conservation rule, which is an element of the conservation of the canonical angular momentum, we find that each gamma photon carries a magnetic flux quantum of 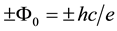 with itself along the propagation direction. Here, the (+) and (−) signs stand for the right and left hand circular helicity respectively. The aim of the present work is to calculate the magnetic moment of any photon through the magnetic moment of a gamma photon and to find a unique relation between the intrinsic fluxes and the magnetic moments of electron, positron and photon.
with itself along the propagation direction. Here, the (+) and (−) signs stand for the right and left hand circular helicity respectively. The aim of the present work is to calculate the magnetic moment of any photon through the magnetic moment of a gamma photon and to find a unique relation between the intrinsic fluxes and the magnetic moments of electron, positron and photon.
The first experiment about the magnetic moment of a photon was done in 1896 by Zeeman [2] , who discovered the spectral lines from sodium. When it was put in a flame, the light emitted was split up into several components in a strong magnetic field. A long period after Zeeman, experimental attempts about photon’s magnetic moment through the Stern-Gerlach experiment (SGE) with photons have started recently by Karpa et al. [3] - [5] .
SGE was devised in 1922 to show that electron had a non-zero magnetic moment [6] and later it was also extended to the nuclei [7] . In general, in the SGE the magnetic field gradient serves as a detector for the particle’s magnetic moment vector: If the magnetic field is a non-uniform field along the z direction such as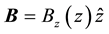 , then because of the torque
, then because of the torque 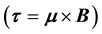 on the particles, the magnetic moment vector can have z-component only:
on the particles, the magnetic moment vector can have z-component only: 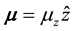 (where
(where 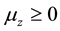 or
or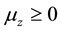 ). On the other hand, the potential energy
). On the other hand, the potential energy 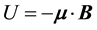 produces a force
produces a force
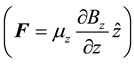 which has quantized values as
which has quantized values as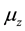 . Depending on whether (
. Depending on whether (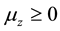 or
or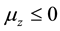 ), the particles
), the particles
are deflected upward or downward. In the SGE with electron, the electron beam is deflected into two sub-
beams which means that 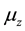 takes only two possible quantized values which are equal to
takes only two possible quantized values which are equal to 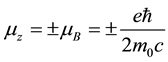
where 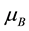 is called the Bohr magneton. Because of the negative charge of the electron, the relation between spin and the magnetic moment is set as
is called the Bohr magneton. Because of the negative charge of the electron, the relation between spin and the magnetic moment is set as 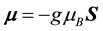
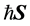
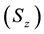
only two possible values which are: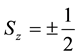
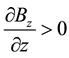
lected upward while the spin-up ones will be deflected downward. Similarly if we have SGE with a positron beam, because of the positive charge, the spin-down positrons will be deflected downward while the spin-up ones will be deflected upward. But when it comes to the gamma photons, which are the composite particles made up of an electron and a positron, the direction of the deflection is determined by the sign of the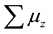
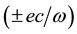
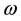
We have also found a unique relation between the intrinsic fluxes and the magnetic moments of the particles such as electron, positron and the photon. We show that for all these three particles the unique relation between the intrinsic fluxes and the magnetic moments is given by: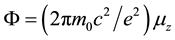
We argue that any photon propagating in z direction with an angular frequency 
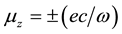
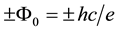

Because of the two symmetric values of the magnetic moment of a photon, we expect a splitting (deflection) of the beam into two symmetric subbeams in a Stern-Gerlach experiment. We also expect that the splitting will be more prominent for lower energies. We believe that the present work will help to understand the Stern-Gerlach experiment of photons [3] -[5] in detail. In the theoretical side, the present work will bring a new insight to quantum mechanics as well.
Electron-positron (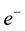
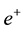


[20] calculated the intrinsic magnetic flux of an electron due to its orbital motion in a non-relativistic hydrogen atom by using the Schrödinger equation and then extended their result to incorporate the spin angular momentum as well.
Most recently Saglam and Sahin [1] calculated the intrinsic quantum fluxes of a free electron and free positron by a semi classical model in the absence of an external magnetic field. As the subject of present study is related to the intrinsic fluxes of 
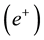
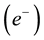
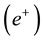
field. We then prove that the intrinsic fluxes of 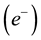
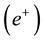
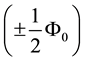
calculations [19] [20] .
In Appendix II, we introduce the conservation of the quantum flux in collisions: We write the Lagrangian of an electron moving in a uniform magnetic field in z direction then calculate the z-component of the conserved canonical angular momentum Jc which has two elements: The conservation of the kinetic angular momentum and the conservation of the magnetic flux. Therefore in the electron-positron annihilation, the conservation of the canonical angular momentum requires both conservation of the spin angular momentum and the conservation of the quantum flux which is originated from the intrinsic fluxes of 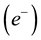
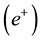
The outline of this paper is as follows: In Section 2, we derive the relation between the intrinsic fluxes and the magnetic moments of electron and positron. In Section 3, we calculate the magnetic moment of photon. In Section 4, we give the conclusions.
2. The Relation between the Intrinsic Fluxes and the Magnetic Moments of an Electron and Positron
The definition of the spin magnetic moment vector 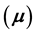

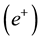
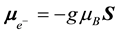
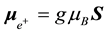
Here, g is the Lande-g factor which is equal to 2 for both particles and 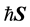
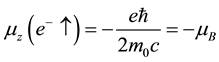
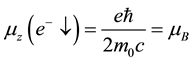
Similarly the related z-components of the magnetic moments for spin-up and down positron are:
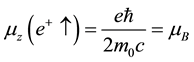
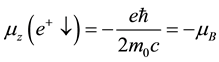
where 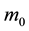
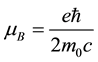
In Appendix I, we calculate the intrinsic fluxes of 
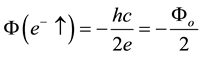

respectively. Similarly the intrinsic fluxes for spin-up and down positron are:

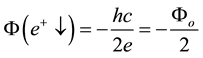
If we compare the z-components of the magnetic moments and the spin dependent fluxes for both electron and positron Equations (2a)-(5b) we write the relation between the intrinsic flux and the magnetic moment of both electron and positron.
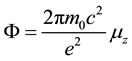
3. Calculation of the Magnetic Moment of a Photon
To calculate the magnetic moment of a photon, our starting point will be the electron-positron annihilation process ending with the creation of two gamma photons with right and left hand circular helicities. After the collision we will have two photons with the same energy 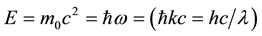


where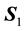
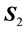
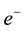
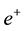
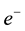
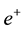
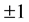
a) The electron is in spin-down state and the positron is in spin-down state.
b) The electron is in spin-up state and the positron is in spin-up state.
In Dirac notation, the states (a) and (b) can be defined as:
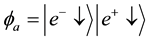
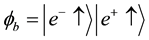
which build an orthonormalized set. Namely
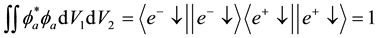
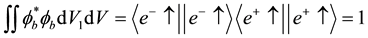
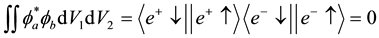
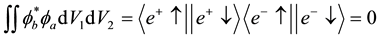
where 
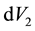
The expectation values of the total z-components of the spin 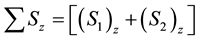
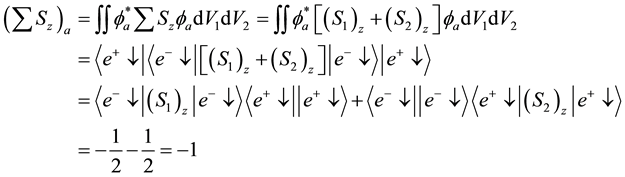
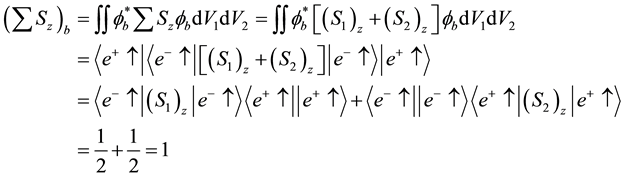
where 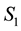
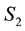
Since the states (a) and (b) are equally probable, the total wave function 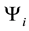
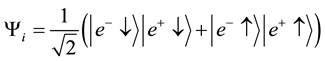
which is the quantum entanglement of the states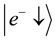
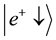
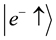
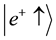
The expectation value of 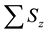
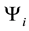
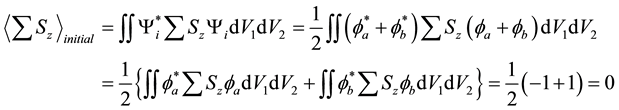
where we used Equations (9a), (9b).
The total wave function, 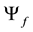
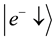
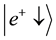

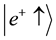
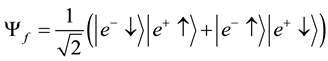
This corresponds to two different gamma photons created with opposite circular helicities [1] . The eigenstates corresponding to the right hand and left circular helicities are:
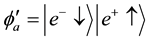
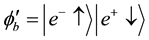
respectively.
As we calculated in Equations (9a), (9b), the expectation values of the total z-components of the spin 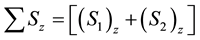
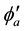


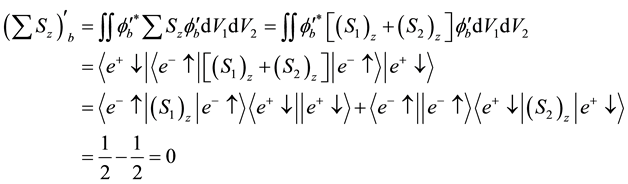
The expectation value of 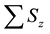
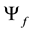

where we used Equations (14a) and (14b).
If we compare the expectation value of 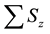
Now using the Equations (2a)-(3b) we can calculate the expectation values of the z-components of the magnetic moment vectors for the eigenstates
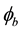

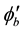
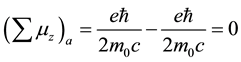


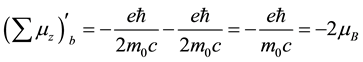
Next, using the Equations (16a)-(16d) we can calculate the expectation value of 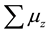
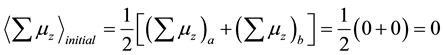

If we compare the expectation value of 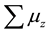
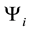
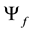
As we stated above, the final state wave function given in Equation (12) corresponds to two different gamma photons created with opposite circular helicities after the collision. Because the eigenstate
corresponds to the gamma photon with the right hand circular helicity and the second eigenstate
corresponds to the gamma photon with the left hand one.
From the Equations (16c) and (16d), the z-component of the magnetic moment of the eigenstates, 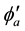
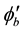

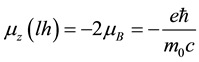
respectively.
Now substituting the relation 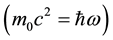
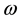
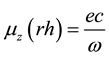
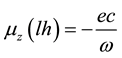
which must be true for any photon also. Namely a photon propagating in z direction with an angular frequency 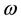
4. Conclusions
We have calculated the intrinsic magnetic moment of a photon through the intrinsic magnetic moment of a gamma photon created as a result of the electron-positron annihilation with the angular frequency w. We show that a photon propagating in z direction with an angular frequency 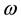
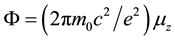
Since for a photon mz is inversely proportional to the angular frequency w, a lower frequency implies a higher magnetic moment. Therefore in the first experiment done by Zeeman [2] in 1896, yellow light of sodium which was in the low frequency range of the optical spectrum was a right choice for that purpose. On the other hand although we used gamma photons to calculate the magnetic moment of a photon, we believed that a Stern-Gerlach experiment (SGE) with gamma photons was almost impossible as we had an extremely high frequency. Because of these two symmetric values of the magnetic moment, we expect a splitting of the photon beam in two symmetric subbeams in a Stern-Gerlach experiment. The splitting is expected to be more prominent for low energy photons. We believe that the present result will be helpful for understanding of the Stern-Gerlach experiment with photons [3] -[5] and also the behavior of the dark polaritons and the atomic spinor polaritons which is useful for the storage of the photonic qubits in a single atomic ensemble. A more complete work will be presented in the future.
Acknowledgements
The authors express their thanks to Professor Mesude Saglam for her encouragement and for her invaluable help.
References
- Saglam, M. and Sahin, G. (2009) International Journal of Modern Physics B, 23, 4977-4985. http://dx.doi.org/10.1142/S0217979209053862
- Zeeman, P. (1897) Nature, 55, 357.
- Karpa, L. and Weitz, M. (2008) New Journal of Physics, 10, Article ID: 045015. http://dx.doi.org/10.1088/1367-2630/10/4/045015
- Karpa, L. and Weitz, M. (2007) IEEE, 17, 1.
- Karpa, L. and Weitz, M. (2006) Nature Physics, 2, 332-335. http://dx.doi.org/10.1038/nphys284
- Gerlach, W. and Stern, O. (1922) Zeitschrift für Physik, 9, 353-355. http://dx.doi.org/10.1007/BF01326984
- Sidles, J.A. (1992) Physical Review Letters, 68, 1124. http://dx.doi.org/10.1103/PhysRevLett.68.1124
- Einstein, A. Podolsky, B. and Rosen, N. (1935) Physical Review, 47, 777. http://dx.doi.org/10.1103/PhysRev.47.777
- Bohr, N. (1935) Physical Review, 48, 696. http://dx.doi.org/10.1103/PhysRev.48.696
- Schrödinger, E. (1935) Proceeding of the Cambridge Philosophical Society, 31, 555-563. http://dx.doi.org/10.1017/S0305004100013554
- Von Neumann, J. (1955) Mathematical Foundations of Quantum Mechanics. Princeton University Press, Princeton.
- Bohm, D. and Aharonov, Y. (1957) Physical Review, 108, 1070-1076. http://dx.doi.org/10.1103/PhysRev.108.1070
- Bell, J.S. (1964) Physics, 1, 195-200.
- Trimmer, J.D. (1980) Proceeding of the American Philosophical Society, 124, 323-328.
- Fine, A. (1982) Physical Review Letters, 48, 291-295. http://dx.doi.org/10.1103/PhysRevLett.48.291
- Fine, A. (1996) The Shaky Game: Einstein, Realism and the Quantum Theory. 2nd Edition, University of Chicago Press, Chicago. http://dx.doi.org/10.7208/chicago/9780226923260.001.0001
- London, F. (1950) Superfluids. John Wiley and Sons, New York.
- Onsager, L. (1954) General Discussion on Superconductivity. Proceeding of the International Conference on Theoretical Physics, Science Council of Japan, Tokyo, 935-936.
- Saglam, M. and Boyacioglu, B. (2002) International Journal of Modern Physics B, 16, 607-614. http://dx.doi.org/10.1142/S0217979202010038
- Wan, K.K. and Saglam, M. (2006) International Journal of Theoretical Physics, 45, 1132-1151. http://dx.doi.org/10.1007/s10773-006-9118-z
- Yilmaz, O., Saglam, M. and Aydin, Z.Z. (2007) Old and New Concepts of Physics, 4, 141-152. http://dx.doi.org/10.2478/v10005-007-0007-x
- Slater, J.C. (1930) Physical Review, 36, 57-64. http://dx.doi.org/10.1103/PhysRev.36.57
Appendix I: Calculation of the Intrinsic Quantum Fluxes of Electron and Positron by Dirac Equation
Solution of Dirac Equation for a free electron moving in a homogeneous magnetic field was given by Saglam et al. [21] :
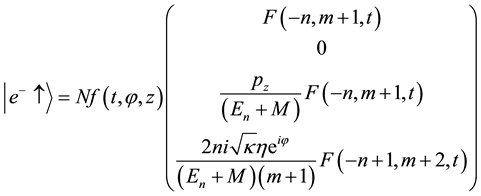
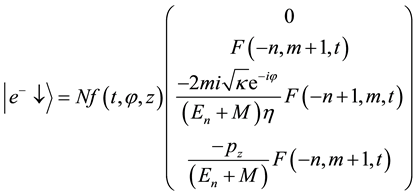
To calculate the intrinsic quantum flux of a relativistic free electron in a uniform magnetic field within the framework of Dirac theory, we shall follow a similar way that we followed earlier [20] : Namely, we shall first calculate the quantum flux through the probability current (particle current) density associated with the wave function of a free Dirac electron in a uniform magnetic field, then connect it to the flux element 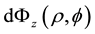
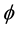

Assuming that electron is moving in 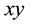

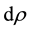
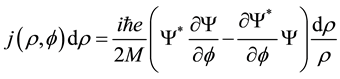
Our next objective is to establish a quantized magnetic flux coming from the above current. A current element circulating around z-axis in a circle of radius 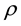
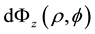
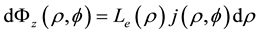
where 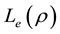
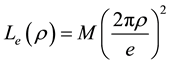
Substitution of Equations (AI-3) and (AI-6) into Equation (AI-5) gives the total induced quantized magnetic flux:
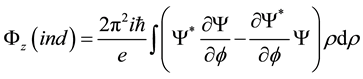
To calculate the total induced quantized magnetic fluxes for spin-up and spin-down electrons, we substitute the wave functions of 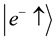
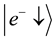
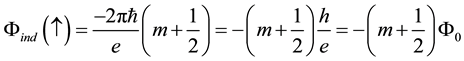

In Equations (AI-8a) and (AI-8b), the spin dependent intrinsic fluxes correspond to m = 0, which are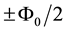
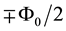

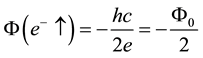
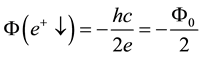

Appendix II: Conservation of the Canonical Angular Momentum in Terms of the Quantum Flux and the Magnetic Moment
The Lagrangian of an electron with mass 
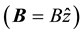
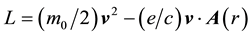
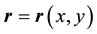
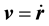
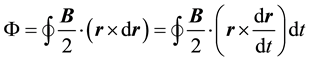
For an electron moving in the x-y plane in the counter clockwise direction with the angular frequency
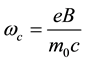
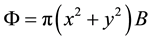

The vector potential, 
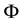
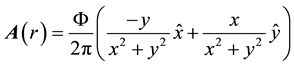
The z-component of the conserved canonical angular momentum Jc is given by

where J is the gauge invariant kinetic angular momentum of the electron.
Now using the relation in Equation (6):
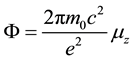
We can write the conserved canonical angular momentum Jc in terms of the magnetic moment. Substitution of Equation (6) into (AII-3) gives:
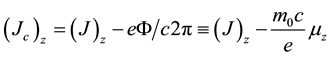
Here, Equations (AII-3) and (AII-4) simply state that the conservation of the canonical angular momentum requires also the conservation of the magnetic flux and the magnetic moment as well. In passing, we note that although the above calculations are carried out for an electron, the statement about the conservation of the magnetic flux and the magnetic moment will be valid for a positron as well. The only difference is that, for a positron the (−) signs in Equations (AII-3) and (AII-4) are replaced with the (+) signs.