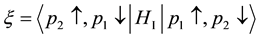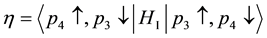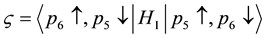Journal of Modern Physics
Vol.06 No.06(2015), Article ID:56571,16 pages
10.4236/jmp.2015.66085
Spin Polarization of Fractional Quantum Hall States with ν < 2
Shosuke Sasaki
Center for Advanced High Magnetic Field Science, Graduate School of Science, Osaka University, Osaka, Japan
Email: sasaki@mag.ahmf.sci.osaka-u.ac.jp, zazensou@gmail.com
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 26 March 2015; accepted 22 May 2015; published 25 May 2015
ABSTRACT
The spin polarization of a fractional quantum Hall state shows very interesting properties. The curve of polarization versus magnetic field has wide plateaus. The fractional quantum Hall effect is caused by the Coulomb interaction because the 2D electron system without the Coulomb interaction yields no energy gap at the fractional filling factor. Therefore, the wide plateau in the polarization curve is also caused by the Coulomb interaction. When the magnetic field is weak, some electrons have up-spins and the others down-spins. Therein the spin-exchange transition occurs between two electrons with up and down spins via the Coulomb interaction. Then the charge distribution before the transition is the same as one after the transition. So these two states have the same classical Coulomb energy. Accordingly, the partial Hamiltonian composed of the spin exchange interaction should be treated exactly. We have succeeded in diagonalizing the spin exchange interaction for the first and second nearest electron pairs. The theoretical results reproduce the wide plateaus very well. If the interval modulations between Landau orbitals are taken into the Hamiltonian, the total energy has the Peierls instability. We can diagonalize the Hamiltonian with the interval modulation. The results reproduce wide plateaus and small shoulders which are in good agreement with the experimental data.
Keywords:
Spin Polarization, Fractional Quantum Hall Effect, 2D Electron System, Quantum Theory

1. Introduction
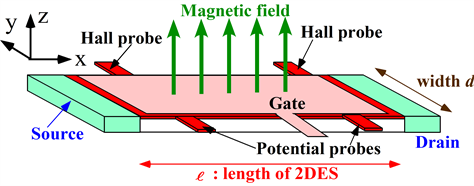
As well known, the integer and fractional quantum Hall effects (IQHE and FQHE) appear in a quasi-two dimensional electron system under a strong magnetic field perpendicular to the 2D electron channel the thickness of which is extremely thin [1] -[17] . Only the ground state along the z-direction of Figure 1 is realized actually for a low temperature and so we can treat the system as a 2D electron system. The confinement of the Hall resistance
Figure 1. Quantum hall device.
at IQHE is extremely accurate and then the confined resistance is employed as the resistance standard [18] . The IQHE and FQHE are observed in various materials namely Si, GaAs, graphene and so on. The QHE appears independently of materials and is caused only by many electrons in a thin film. The Hall resistance is the ratio between Hall voltage and electric current. In the IQHE the Hall voltage is larger than about 10−4 Volts and the diagonal (potential) voltage is less than 10−11 Volt. Also in the FQHE the Hall voltage is extremely large compared with the potential voltage. Therefore this asymmetry of x and y directions in Figure 1 should be taken into consideration in the investigations of QHE. Consequently the total Hamiltonian of many electrons should be composed of three kinds of interactions namely the strong magnetic field interaction, the Coulomb interactions between electrons, and the electric field produced by the Hall voltage. However, many theories ignore the electric field along the Hall voltage. We take account of the electric potential along the y-direction in Figure 1.
We have developed the theory of Tao and Thouless [19] [20] and have found out the most uniform configuration of electrons in the Landau orbitals which yields the minimum expectation value of the total Hamiltonian 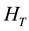 [21] -[25] . Since the Coulomb interaction depends only upon the relative coordinate between two electrons, the
[21] -[25] . Since the Coulomb interaction depends only upon the relative coordinate between two electrons, the  component of the total momentum is conserved in the Coulomb transition. Because of the momentum conservation and the most uniform configuration, the number of the allowed transitions takes the local maximum at the specific filling factors
component of the total momentum is conserved in the Coulomb transition. Because of the momentum conservation and the most uniform configuration, the number of the allowed transitions takes the local maximum at the specific filling factors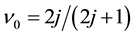 ,
, 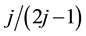 ,
, 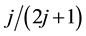 ,
, 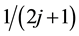 ,
, 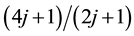 ,
, 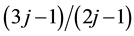 ,
, 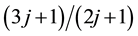 ,
, 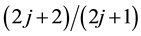 and so on. The transitions produce the binding energy of the electron pair. The larger the number of transitions, the pair energy is lowered. If the filling factor
and so on. The transitions produce the binding energy of the electron pair. The larger the number of transitions, the pair energy is lowered. If the filling factor 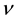 deviates from the specific filling factors
deviates from the specific filling factors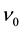 , many Coulomb transitions are forbidden. The forbidden mechanism yields the energy gap at the specific filling factors
, many Coulomb transitions are forbidden. The forbidden mechanism yields the energy gap at the specific filling factors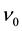 . Thereby, the Hall confinement appears at the specific filling factors. Thus the present theory can explain the FQHE well without any quasi-particle [21] -[26] .
. Thereby, the Hall confinement appears at the specific filling factors. Thus the present theory can explain the FQHE well without any quasi-particle [21] -[26] .
The spin-polarizations of FQHE are obtained by V. Kukushkin, K. von Klitzing, and K. Eberl [27] . They clarified the magnetic field dependence of the polarization under fixing the filling factors. Although their experiments are rather old, the polarization curves versus magnetic field give us the very important knowledge. The experimental polarization-curves have the wide plateaus and small shoulders.
There are many spin-arrangements in the most uniform configuration of electrons in the Landau orbitals. These spin-arrangements have the same minimum-expectation-value of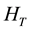 . That is to say many electron states with various spin-arrangements are perfectly degenerate. Therefore, we should exactly diagonalize the residual Coulomb interaction. We examine the partial Hamiltonian composed of the strongest and second strongest interactions between electrons. Then we have succeeded to diagnalize the Hamiltonian exactly. The theoretical results are in good agreement with the experimental data. Recently J. K. Jain has written the article [28] and compared the composite fermion (CF) theory [29] -[44] with the Haldane-Halaperin (HH) hierarchy theory [45] [46] . Also he summarized the composite fermion theory and showed the theoretical results on the spin-polarization of FQH states. We compare the polarizations by the CF theory with that by our theory in Section 5.
. That is to say many electron states with various spin-arrangements are perfectly degenerate. Therefore, we should exactly diagonalize the residual Coulomb interaction. We examine the partial Hamiltonian composed of the strongest and second strongest interactions between electrons. Then we have succeeded to diagnalize the Hamiltonian exactly. The theoretical results are in good agreement with the experimental data. Recently J. K. Jain has written the article [28] and compared the composite fermion (CF) theory [29] -[44] with the Haldane-Halaperin (HH) hierarchy theory [45] [46] . Also he summarized the composite fermion theory and showed the theoretical results on the spin-polarization of FQH states. We compare the polarizations by the CF theory with that by our theory in Section 5.
Next we observe the experimental data [27] in more details. Then we find small shoulders on the curves of the polarization versus magnetic field. The small shoulders appear at the middle between two wide plateaus. This property is similar to the famous feature in the spin-Peierls effect [47] . The spin-Peierls effect is caused by the lattice distortion with the period doubling the unit cell. The sum of spin-energy and distortion-energy (namely total energy) becomes lower than that without distortion. We applied the distortion to the intervals between Landau orbitals in the previous works [48] [49] where the magnitude of distortion was treated to be a fixed value. However the magnitude should be determined by minimizing the total energy in each field strength. Accordingly the magnitude of distortion depends on the field strength. The minimizing of the total energy needs a very complicated program and a long cpu-time. In this article we succeed to make the Mathematica program with parallel computation. The calculated results show the Peierls instability and the polarization curves are in better agreement with the experimental data than the previous results.
2. Fundamental Properties
A typical quantum Hall device is illustrated in Figure 1 where the current flows along the x-direction and the magnetic field  has the z-direction, namely
has the z-direction, namely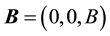
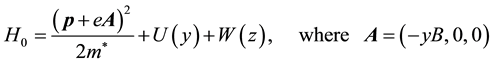
Therein 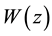
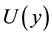
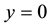
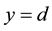
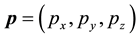
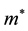
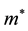
The eigen-value problem of 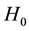
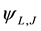
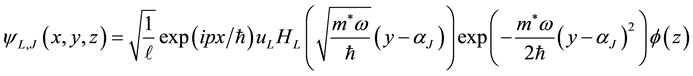
where 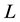
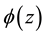
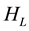
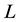
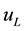
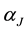
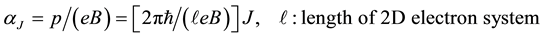
The eigenenergy is given by
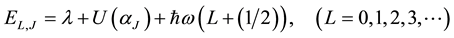
where 
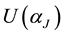
Next let us consider the many electron system. The total Hamiltonian is given by
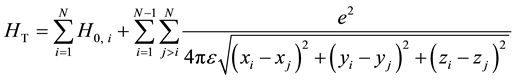
where 
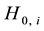
The eigenstate of 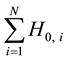
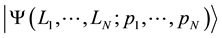
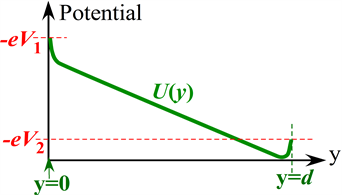
Figure 2. Potential 
level numbers 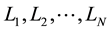
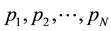
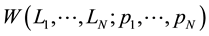
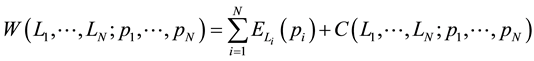
where 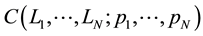
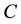
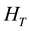
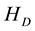
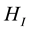
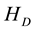
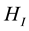
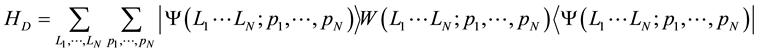
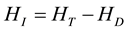
Because the Coulomb interaction depends upon only the relative coordinate, the total momentum of the x-direction is conserved in this system as follows:
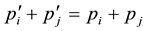
where 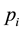
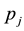
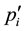
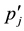
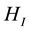
in the ground state of 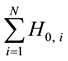
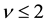
electrons can take up- and down-spin states. If the electrons with the momenta 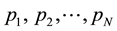
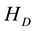
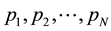
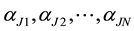
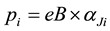
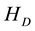
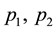
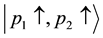
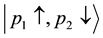
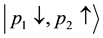
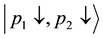
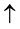
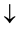
spectively. The final states are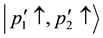
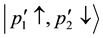
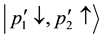
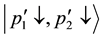
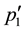
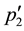
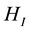
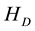
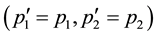
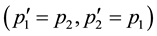
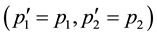
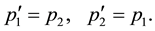
Even if Equation (9) is satisfied, the initial state is identical to the final state for the same spin direction of the two electrons. Therein the transition matrix element is zero. Accordingly non-zero matrix elements are
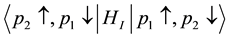
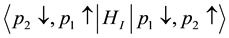
where
Case A: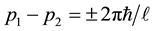
Case B: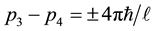
Case C: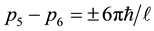
Figure 3 shows the case A.
This transition is equivalent to the following process: the spin at site 1 flips from up to down, and the spin at site 2 flips from down to up without changing the momenta. Thus the Coulomb transition of the case A is equivalent to a spin exchange process which is described by the interaction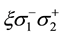
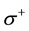
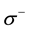
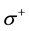
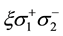
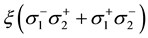
where 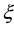
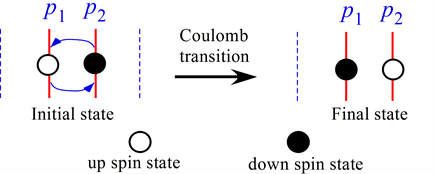
Next Figure 4 shows the case B.
Coulomb interactions in Cases B and C are equivalent to the following spin exchange interactions where 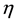
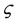

Let us study two examples of 
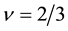
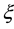
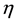
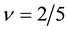
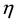
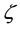
We examine the third strongest interaction at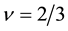
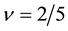
Figure 3. Equivalence of specific Coulomb transition and spin exchange interaction for case A.
Figure 4. Equivalence of specific Coulomb transition and spin exchange interaction for case B.
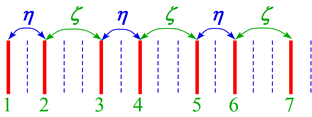
Figure 5. (a) Coulomb transitions at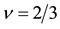
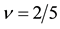
becomes weak by the screening effect of the interposing electron. Consequently the most effective interaction is obtained for 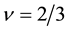
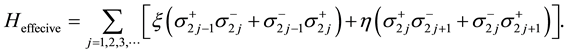
This Hamiltonian yields the quantum transition between the degenerate ground states. We take account of the Zeeman interaction and get the most effective Hamiltonian as
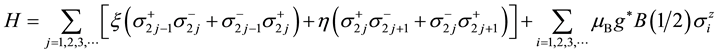
where 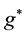
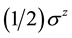
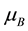
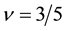
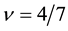
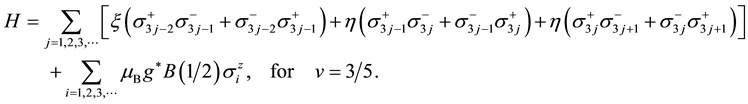
These three Hamiltonians can be exactly diagonalized by using the method of Ref. [50] .
3. Diagonalization of the Most Effective Hamiltonian for FQH States
We introduce a new mapping from a spin state to a fermion state. The down-spin state 

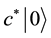
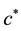
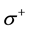
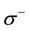
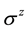
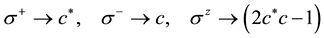
Many electron states are mapped to the many fermion states where the multiplying order of the creation operators is the same as the order of the up-spins:
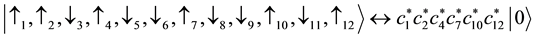
where the operators 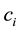
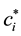
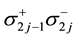
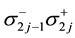
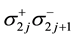
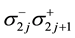
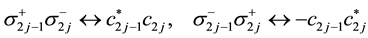
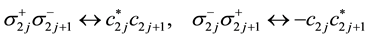
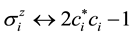
It has been verified in Ref. [50] that the mapping ((20a), (20b), (20c)) is isomorphic.
Accordingly Hamiltonian Equation (15) is equivalent to the following form:
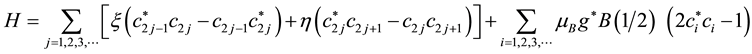
We can exactly solve the eigen-value problem of 
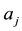
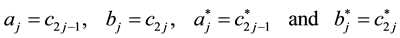
where 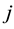
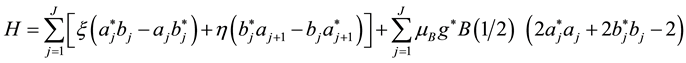
where 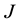
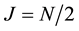
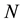
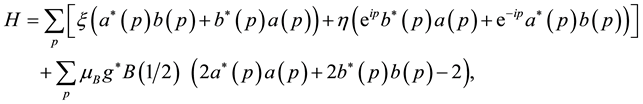
where
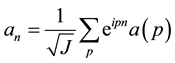
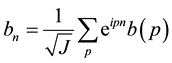
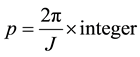
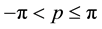
In Equation (24) the term with one value of 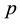
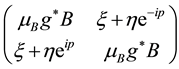
This matrix has two eigen-values 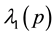
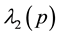
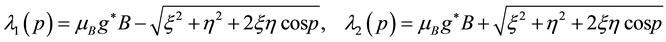
We introduce new annihilation operators 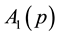
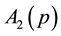

Hamiltonian (24) is expressed by making use of 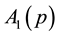
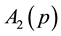
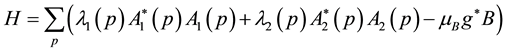
Thus we have succeeded in diagonalizing the original Hamiltonian (15).
4. Spin-Polarization
The electron-spin polarization 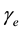
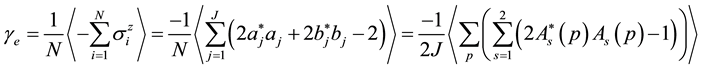
where 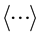
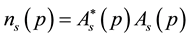
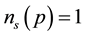
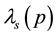
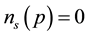
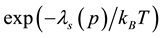
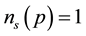
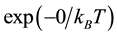
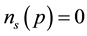
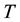
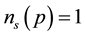
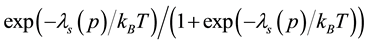
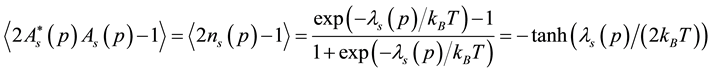
Substitution of Equation (31) into Equation (30) gives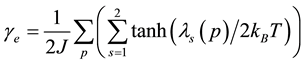
momentum interval is extremely small, the electron-spin polarization is expressed by the integration as
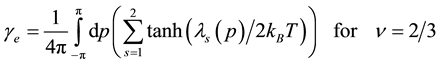
Similarly we obtain the spin-polarization at the filling factors of 3/5 and 4/7 as follows:
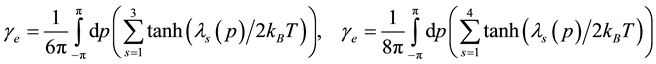
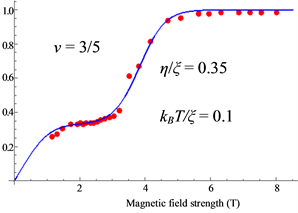
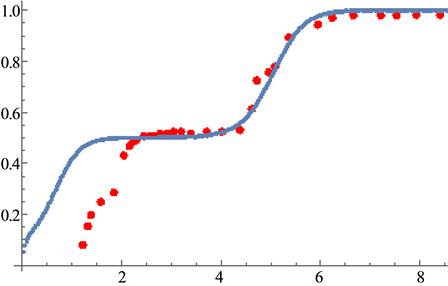
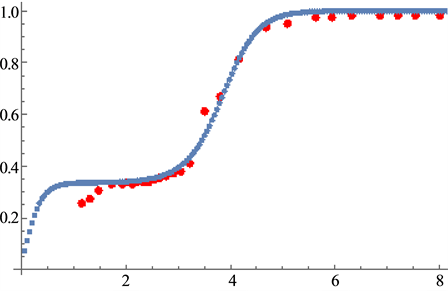
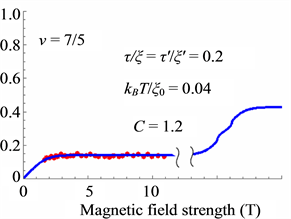
The calculated results are shown in Figure 6 which are in good agreement with the experimental data.
5. Comparison between Present Theory and Composite Fermion Theory
J. K. Jain examined the spin-polarization in the CF theory [28] . He wrote as follows: “For spinful composite fermions, we write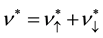
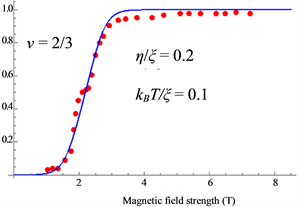
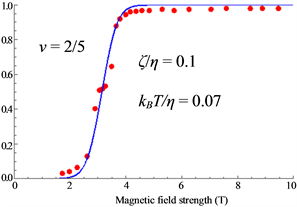
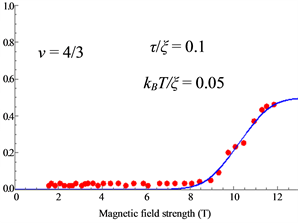
Figure 6. (a) Polarization at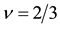
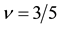
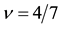
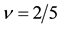

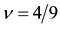
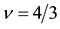
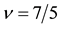
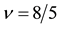
spinful electrons. For example, the 4/7 state maps into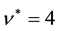
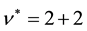
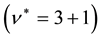
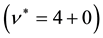
The CF cyclotron energy is proportional to 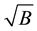
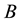
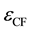
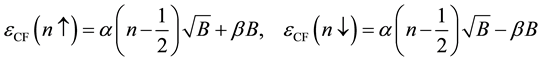
where 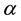
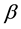

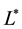
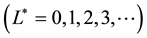

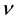
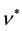
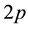
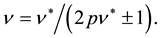
When the sign in the denominator is plus, the effective magnetic field is parallel to the applied magnetic field. So the coefficient 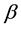
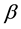
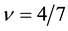
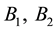
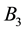
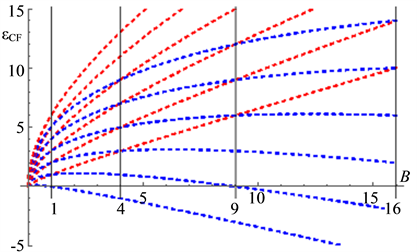
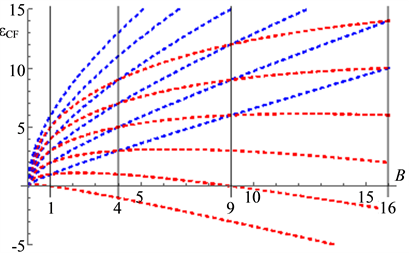
Figure 7. (a) Energy of CF for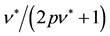
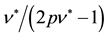
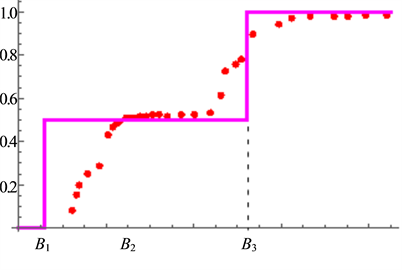
Figure 8. (a) Ground state in CF theory at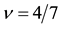
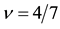
It is noteworthy that the effective field is opposite against the applied field at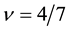
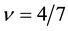
Similarly we compare the CF result with our result at 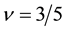
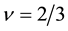
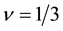
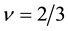
6. Spin Peierls Instability in FQH States
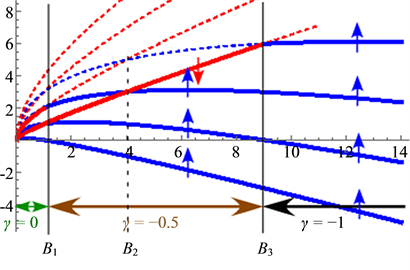
When the experimental data [27] of the spin polarization is carefully observed, we can find a small shoulder in the middle of two wide plateaus. This structure resembles the famous mechanism “spin Peierls effect”. R. E. Peierls studied an electron system in a one dimensional crystal and considered the lattice distortion with the period doubling the unit cell. This distortion produces new band gaps and the energy becomes lower than without the distortion. The effect is called spin Peierls effect [47] .
We apply a new distortion for the intervals between Landau orbitals. We change the distance between orbitals in the first unit-configuration longer, that in the second unit-configuration shorter and so on. We call it “interval modulation”. As an example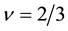
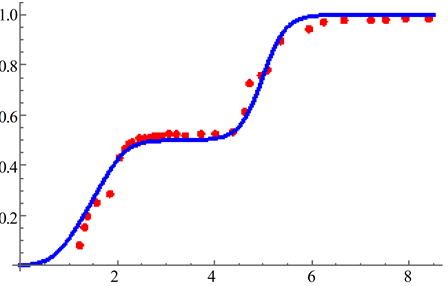
Figure 9. (a) CF result at 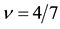
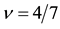
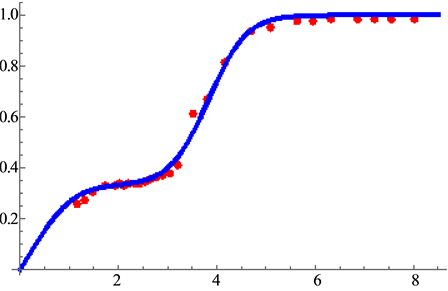
Figure 10. (a) CF result at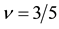
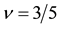
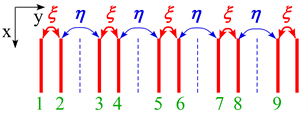
ξ η ξ' η' ξ η ξ' η'
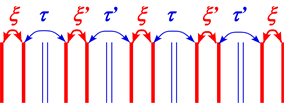
Figure 11. Coupling constants of interactions caused by distortion with double period.
coupling constants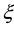
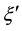
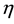
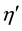
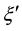
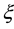
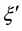
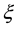
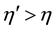
We express the distance between nearest Landau orbitals by the symbol 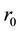
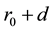
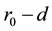
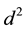
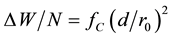
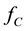
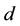
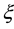
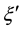
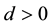
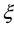
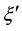
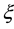
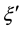
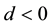
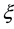
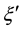
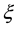
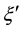
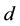
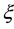
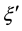
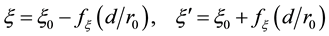
where 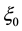
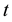
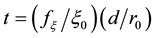
Thereby the coupling constants 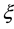
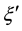
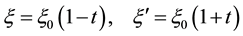
The increasing classical Coulomb-energy 
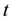
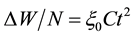
where 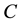
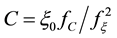
We calculate the total energy produced by this distortion. Use of the isomorphic mapping namely Equations ((20a), (20b), (20c)) give the spin exchange Hamiltonian for
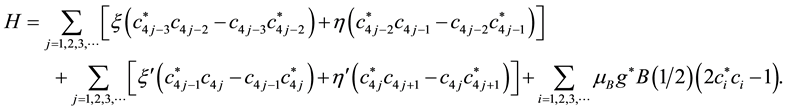
We introduce new operators 
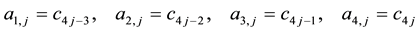
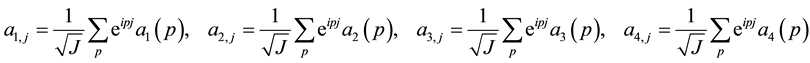
where 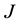
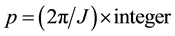
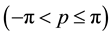
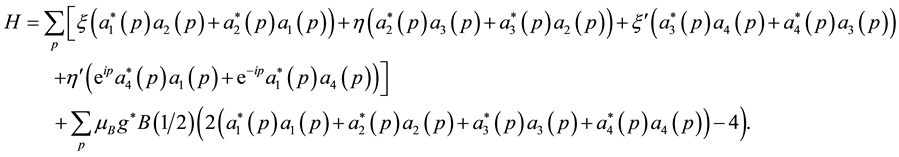
For each value of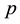
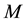
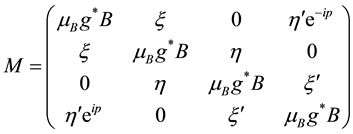
Here we assume that the ratio 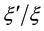
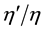
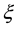
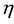
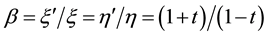
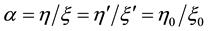
Four eigen-values of M are expressed by the symbols λ1(p), λ2(p), λ3(p) and λ4(p)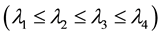
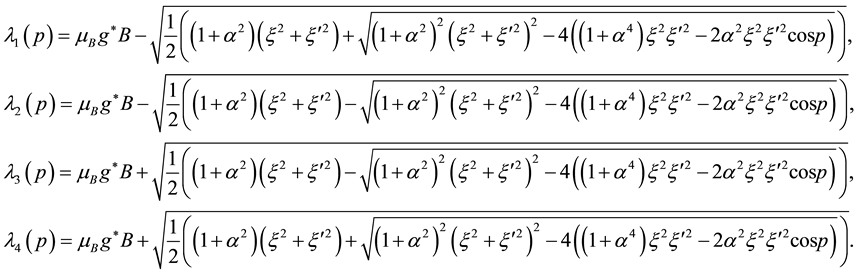
Then the diagonal form of the Hamiltonian (43) is expressed by the eigen-energies λ1, λ2, λ3, λ4 as:
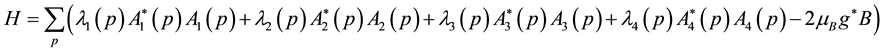
The thermal average 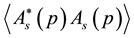
Then the spin exchange energy is
We can replace the summation in Equation (49) by the integration because the total number of electrons is a macroscopic value.
The total energy per electron is the sum of the classical Coulomb energy and the spin energy as
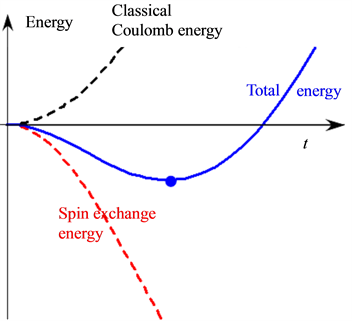
Figure 12 shows the classical Coulomb energy for the parameter 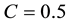
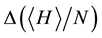
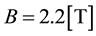
The blue curve indicates the total energy 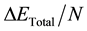
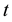
The 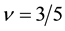
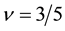
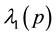
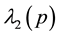
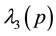
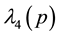
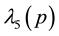
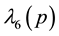
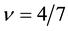
7. Spin Polarization with Interval Modulation
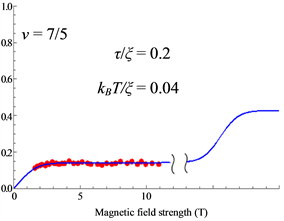
We have obtained the diagnal forms of the Hamiltonians which have the Peierls instability. The spin-polarization 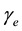
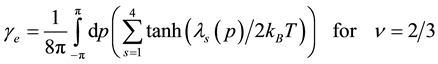
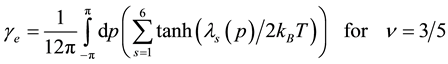
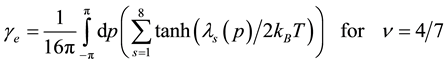
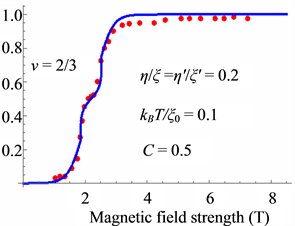
We numerically calculate the spin-polarization 
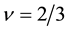
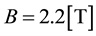
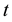
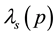
Therein we use the parameter-values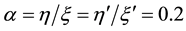
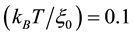
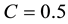
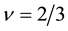
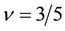
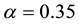
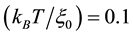
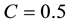
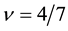
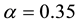

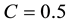
Next we examine the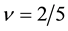
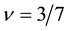
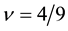
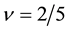
Figure 12. Total energy versus distortion parameter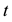
ξ η η ξ' η' η' ξ η η ξ' η' η'
Figure 13. Coupling constants for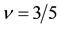
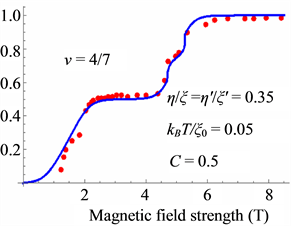
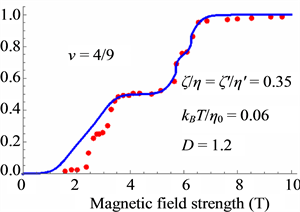
Figure 14. Polarization of the present theory (red dots indicate the experimental data [27] ).
η ζ η' ζ' η ζ η' ζ'
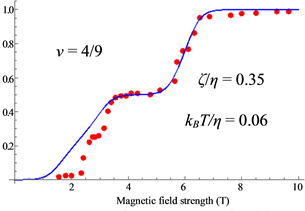
Figure 15. Coupling constants for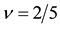
The interval modulation yields the coupling constants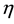
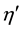
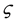
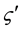
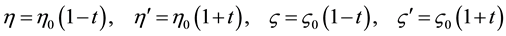
The ratios between the coupling constants satisfy the following relations;
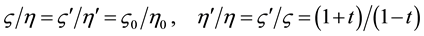
We express the spin-exchange and classical Coulomb energies by the same parameter 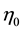
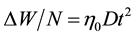
Therein the coefficient 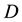
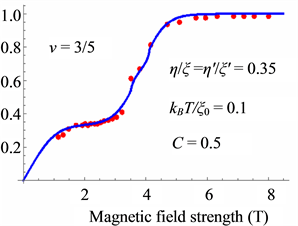
Next we examine the spin-polarization at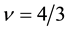
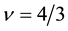
The coupling constants at 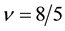
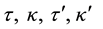
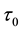
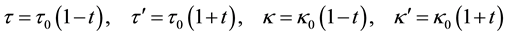
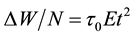
where the new coefficient 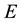
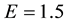
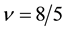
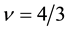
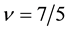
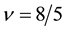
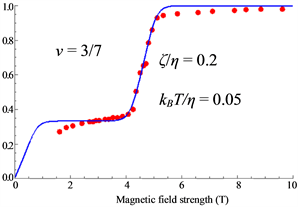
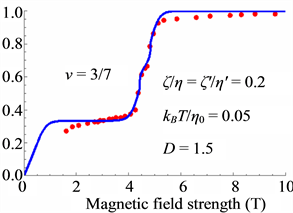
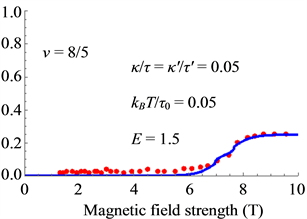
Thus the small shoulders are caused by the Peierls instability as seen in Figure 14, Figure 16 and Figure 18.
The theoretical results are in good agreement with the experimental data.
8. Discussion
In Jain’s scheme the 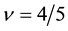
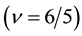
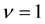
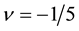
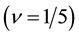
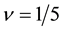
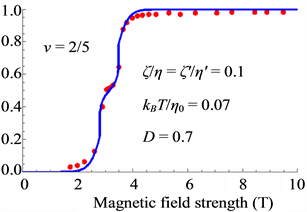
Figure 16. Spin-polarization for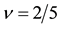
Figure 17. Coupling constants at 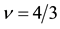
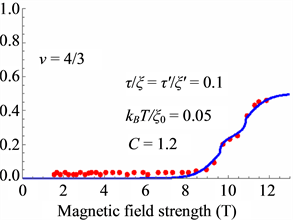
Figure 18. Spin-polarization for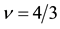
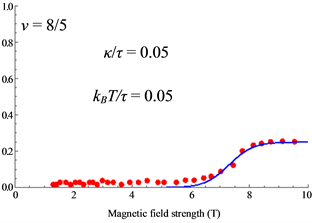
polarization behavior of the present theory at 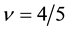
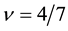
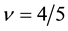
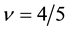
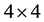
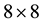
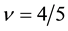
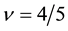
We cannot also find the experimental data of the spin direction. The effective magnetic field in the CF theory is opposite against the applied field for the filling factor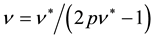
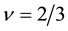
9. Conclusions
We have examined the 2D electron system with the total Hamiltonian composed of the three kinds of interactions namely the strong magnetic field interaction, the Coulomb interaction between electrons and the electric potential produced by the Hall voltage. We have found only one electron configuration in the Landau orbitals with the minimum expectation value of the total Hamiltonian for arbitrary filling factor. Up and down spins coexist when the magnetic field is weak. Accordingly there are various spin-arrangements with the same electron configuration. The many states with different spin-arrangements have the same Coulomb energy namely exactly degenerate states. Accordingly we must diagonalize the partial Hamiltonian between the degenerate ground states.
The total momentum along the x-direction conserves via the Coulomb interactions. When the electron 1 placed in the Landau orbital A transfers to the orbital B, the electron 2 placed in the orbital B should transfer to the orbital A because of the total momentum conservation and the relation between momentum and orbital position. We have found the most effective Hamiltonian which is composed of the strongest and second strongest Coulomb interactions. Then we have succeeded to diagonalize the most effective Hamiltonian exactly. The calculated eigen-energies yield the theoretical value of the polarization which has reproduced the wide plateaus on the spin polarization curves. Furthermore we have applied the interval modulation between Landau orbitals and have solved the eigen-equation of the new Hamiltonian. The total energy decreases by the interval modulation. So the modulation appears actually. Thereby the calculated polarization curves have the small shoulders in addition to the wide plateaus. The theoretical results are in good agreement with the experimental data [27] .
Acknowledgements
The author expresses his heartfelt appreciation for encouragement of Professor Masayuki Hagiwara, Professor Koichi Katsumata, Professor Hidenobu Hori, Professor Yasuyuki Kitano and Professor Takeji Kebukawa.
References
- von Klitzing, K., Landwehr, G. and Dorda, G. (1974) Solid State Communications, 14, 387-393. http://dx.doi.org/10.1016/0038-1098(74)90566-3
- Ando, T., Matsumoto, Y. and Uemura, Y. (1975) Journal of the Physical Society of Japan, 39, 279-288. http://dx.doi.org/10.1143/JPSJ.39.279
- von Klitzing, K., Dorda, G. and Pepper, M. (1980) Physical Review Letters, 45, 494. http://dx.doi.org/10.1103/PhysRevLett.45.494
- Tsui, D.C. and Gossard, A.C. (1981) Applied Physics Letters, 37, 550. http://dx.doi.org/10.1063/1.92408
- Tsui, D.C., Stormer, H.L. and Gossard, A.C. (1982) Physical Review B, 25, 1405. http://dx.doi.org/10.1103/PhysRevB.25.1405
- Tsui, D.C., Stormer, H.L. and Gossard, A.C. (1982) Physical Review Letters, 48, 1559. http://dx.doi.org/10.1103/PhysRevLett.48.1559
- Laughlin, R.B. (1983) Physical Review B, 27, 3383. http://dx.doi.org/10.1103/PhysRevB.27.3383
- Laughlin, R.B. (1983) Physical Review Letters, 50, 1395. http://dx.doi.org/10.1103/PhysRevLett.50.1395
- Girvin, S.M. (1984) Physical Review B, 29, 6012. http://dx.doi.org/10.1103/PhysRevB.29.6012
- von Klitzing, K. (1986) Reviews of Modern Physics, 58, 519-531. http://dx.doi.org/10.1103/RevModPhys.58.519
- von Klitzing, K. (1993) Nobel Lecture, December 9, 1985, The Quantized Hall Effect. In: Frängsmyr, T. and Ekspong, G., Eds., Nobel Lectures, Physics 1981-1990, World Scientific, Singapore, 317.
- Willet, R., Eisenstein, J.P., Stormer, H.L., Tsui, D.C., Gossard, A.C. and English, J.H. (1987) Physical Review Letters, 59, 1776-1779. http://dx.doi.org/10.1103/PhysRevLett.59.1776
- Eisenstein, J.P. and Stormer, H.L. (1990) Science, 248, 1510-1516. http://dx.doi.org/10.1126/science.248.4962.1510
- Stormer, H.L. (2002) Nobel Lecture, December 8, 1998, The Fractional Quantum Hall Effect. In: Ekspong, G., Ed., Nobel Lectures, Physics 1996-2000, World Scientific, Singapore, 295-325.
- Pan, W., Stormer, H.L., Tsui, D.C., Pfeiffer, L.N., Baldwin, K.W. and West, K.W. (2002) Physical Review Letters, 88, Article ID: 176802. http://dx.doi.org/10.1103/PhysRevLett.88.176802
- Pan, W., Stormer, H.L., Tsui, D.C., Pfeiffer, L.N., Baldwin, K.W. and West, K.W. (2003) Physical Review Letters, 90, Article ID: 016801. http://dx.doi.org/10.1103/PhysRevLett.90.016801
- Novoselov, K.S., Jiang, Z., Zhang, Y., Morozov, S.V., Stormer, H.L., Zeitler, U., Maan, J.C., Boebinger, G.S., Kim, P. and Geim, A.K. (2007) Science, 315, 1379. http://dx.doi.org/10.1126/science.1137201
- Jeckelmann, B. and Jeanneret, B. (2001) Reports on Progress in Physics, 64, 1603-1655. http://dx.doi.org/10.1088/0034-4885/64/12/201
- Tao, R. and Thouless, D.J. (1983) Physical Review B, 28, 1142-1144. http://dx.doi.org/10.1103/PhysRevB.28.1142
- Tao, R. (1984) Physical Review B, 29, 636-644. http://dx.doi.org/10.1103/PhysRevB.29.636
- Sasaki, S. (2012) Advances in Condensed Matter Physics, 2012, Article ID: 281371. http://dx.doi.org/10.1155/2012/281371
- Sasaki, S. (2000) Physica B: Condensed Matter, 281-282, 838-839. http://dx.doi.org/10.1016/S0921-4526(99)00840-6
- Sasaki, S. (2011) Binding Energy, Polarization of Fractional Quantum Hall State. Proceedings of the 25th International Conference on the Physics of Semiconductors, Part II, Osaka, 17-22 September 2000, 925-926.
- Sasaki, S. (2003) Surface Science, 532-535, 567-575. http://dx.doi.org/10.1016/S0039-6028(03)00091-8
- Sasaki, S. (2008) Journal of Physics: Conference Series, 100, Article ID: 042021. http://dx.doi.org/10.1088/1742-6596/100/4/042021
- Sasaki, S. (2014) Condensed Matter Physics, 2014, Article ID: 468130.
- Kukushkin, I.V., von Klitzing, K. and Eberl, K. (1999) Physical Review Letters, 82, 3665.
- Jain, J.K. (2014) Indian Journal of Physics, 88, 915-929. http://dx.doi.org/10.1007/s12648-014-0491-9
- Jain, J.K. (1989) Physical Review Letters, 63, 199-202. http://dx.doi.org/10.1103/PhysRevLett.63.199
- Lopez, A. and Fradkin, E. (1991) Physical Review B, 44, 5246-5262. http://dx.doi.org/10.1103/PhysRevB.44.5246
- Halperin, B.I., Lee, P.A. and Read, N. (1993) Physical Review B, 47, 7312-7343. http://dx.doi.org/10.1103/PhysRevB.47.7312
- Schwarzschild, B. (1993) Physics Today, 46, 17-20.
- Du, R.R., Stormer, H.L., Tsui, D.C., Pfeiffer, L.N. and West, K.W. (1993) Physical Review Letters, 70, 2944-2947. http://dx.doi.org/10.1103/PhysRevLett.70.2944
- Jain, J.K. (2007) Composite Fermions. Cambridge University Press, New York. http://dx.doi.org/10.1017/CBO9780511607561
- Das Sarma, S. (1996) Localization, Metal-Insulator Transitions, and Quantum Hall Effect. In: Das Sarma, S. and Pinczuk, A., Eds., Perspectives in Quantum Hall Effects: Novel Quantum Liquids in Low-Dimensional Semiconductor Structures, Wiley, New York, 1-36. http://dx.doi.org/10.1002/9783527617258.ch1
- Jain, J.K. and Kamilla, R.K. (1998) Composite Fermions: Particles of the Lowest Landau Level. In: Heinonen, O., Ed., Composite Fermions: A Unified View of the Quantum Hall Regime, World Scientific, New York, 1-90. http://dx.doi.org/10.1142/9789812815989_0001
- Halperin, B.I. (2004) Fermion Chern-Simons Theory and the Unquantized Quantum Hall Effect. In: Das Sarma, S. and Pinczuk, A., Eds., Perspectives in Quantum Hall Effects: Novel Quantum Liquids in Low-Dimensional Semiconductor Structures, Wiley, New York, 225-263.
- Stormer, H.L. and Tsui, D.C. (1996) Composite Fermions in the Fractional Quantum Hall Effect. In: Das Sarma, S. and Pinczuk, A., Eds., Perspectives in Quantum Hall Effects: Novel Quantum Liquids in Low-Dimensional Semiconductor Structures, Wiley, New York, 285-421. http://dx.doi.org/10.1002/9783527617258.ch10
- Lopez, A. and Fradkin, E. (1998) Fermionic Chern-Simons Field Theory for the Fractional Quantum Hall Effect. In: Heinonen, O., Ed., Composite Fermions: A Unified View of the Quantum Hall Regime, World Scientific, New York, 195-253. http://dx.doi.org/10.1142/9789812815989_0003
- Simon, S.H. (1998) The Chern-Simons Fermi Liquid Description of Fractional Quantum Hall States. In: Heinonen, O., Ed., Composite Fermions: A Unified View of the Quantum Hall Regime, World Scientific, New York, 91-194. http://dx.doi.org/10.1142/9789812815989_0002
- Smet, J.H. (1998) Ballistic Transport of Composite Fermions in Semiconductor Nanostructures. In: Heinonen, O., Ed., Composite Fermions: A Unified View of the Quantum Hall Regime, World Scientific, New York, 443-491. http://dx.doi.org/10.1142/9789812815989_0007
- Jain, J.K. (2000) Physics Today, 53, 39-45. http://dx.doi.org/10.1063/1.883035
- Halperin, B.I. (2003) Physica E: Low-Dimensional Systems and Nanostructures, 20, 71-78. http://dx.doi.org/10.1016/j.physe.2003.09.022
- Murthy, G. and Shankar, R. (2003) Reviews of Modern Physics, 75, 1101-1158. http://dx.doi.org/10.1103/RevModPhys.75.1101
- Haldane, F.D.M. (1983) Physical Review Letters, 51, 605-608. http://dx.doi.org/10.1103/PhysRevLett.51.605
- Halperin, B.I. (1984) Physical Review Letters, 52, 1583-1586. http://dx.doi.org/10.1103/PhysRevLett.52.1583
- Peierls, R.E. (1955) Quantum Theory of Solids. Oxford University, London.
- Sasaki, S. (2004) Surface Science, 566-568, 1040-1046. http://dx.doi.org/10.1016/j.susc.2004.06.101
- Sasaki, S. (2005) Binding Energies and Spin Polarizations of Fractional Quantum Hall States. In: Norris, C.P., Ed., Surface Science: New Research, Nova Science Publishers, Hauppauge, 103-161.
- Sasaki, S. (1996) Physical Review E, 53, 168-178. http://dx.doi.org/10.1103/PhysRevE.53.168