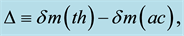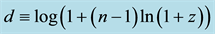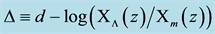Journal of Modern Physics
Vol.06 No.01(2015), Article ID:53590,9 pages
10.4236/jmp.2015.61010
A Possible Alternative to the Accelerating Universe
Frank R. Tangherlini
P.O. Box 928211, San Diego, CA 92192, USA
Email: frtan96@gmail.com
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 4 January 2015; accepted 24 January 2015; published 28 January 2015
ABSTRACT
A possible alternative to the accelerating universe is proposed, which shows that the diminished brightness of the high red shift Type Ia supernovae can be explained by assuming light travels with reduced speed through the dark energy of intergalactic space. It is also shown that support for the  model from baryon acoustic oscillations (BAO) studies can also be accommodated by the model. Two tables are given to compare the model with apparent magnitude differences and length differences between the flat
model from baryon acoustic oscillations (BAO) studies can also be accommodated by the model. Two tables are given to compare the model with apparent magnitude differences and length differences between the flat 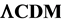 universe and the Einstein-de Sitter universe, and they show that the model yields these differences quite accurately. A third table comparing the apparent magnitude difference between
universe and the Einstein-de Sitter universe, and they show that the model yields these differences quite accurately. A third table comparing the apparent magnitude difference between 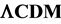 and a universe with
and a universe with  and
and 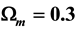 is also given. It exhibits poor agreement with
is also given. It exhibits poor agreement with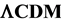 , and hence the model favors the need for dark ener- gy, albeit without negative pressure. As a new approach to the “why now?” problem, and its apparent challenge to the Copernican principle, it is proposed that dark energy is a condensed form of dark matter caused by expansion cooling, rather than a different substance. A motivation for an alternative to
, and hence the model favors the need for dark ener- gy, albeit without negative pressure. As a new approach to the “why now?” problem, and its apparent challenge to the Copernican principle, it is proposed that dark energy is a condensed form of dark matter caused by expansion cooling, rather than a different substance. A motivation for an alternative to  is presented based on a principle that rules out the cosmological term.
is presented based on a principle that rules out the cosmological term.
Keywords:
Accelerating Universe, Alternative Model, Speed of Light, Dark Energy

1. Introduction
This work will give an alternative to the accelerating model of the universe that has been used to describe the diminished brightness of the Type Ia supernovae (SNeIa), when compared to what would be the case in a decelerating universe, that was found by Perlmutter et al. [1] [2] , Riess, et al. [3] , and Schmidt et al. [4] . Although the alternative model agrees with the accelerating model as to the existence of dark energy, it does not associate a negative pressure with the dark energy, as given by the cosmological term, or a suitable form of quintessence, nor does it assume the diminished brightness is due to some form of extinguishing dust or evolution of the SNeIa, as discussed and rejected, e.g., by Riess et al. [5] . A significant feature of the alternative model is that it provides a novel approach to the “why now?” problem that seems to challenge the Copernican principle [6] [7] . This challenge arises because if the universe were accelerating now it would distinguish the present epoch from earlier epochs when this would not have been the case, whereas according to the principle, just as Bondi [6] notes with regard to space, “the Earth is not in a central favored position,” so too it should not be in a favored position in time. To be sure, in the alternative model, the “why now?” question is not understood to ask why the universe is accelerating now, since in the model it is decelerating now, as it was earlier, but rather why do the SNeIa exhibit diminished brightness now (cosmologically speaking) notably at redshift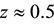 , rather than at, say,
, rather than at, say,  , where the expected brightness of a Type Ia supernova for a decelerating universe is possibly observed [8] ? To further motivate this work, a new argument pointing out a difficulty with the cosmological term that goes beyond the author’s earlier critique [9] is given in Section 2.
, where the expected brightness of a Type Ia supernova for a decelerating universe is possibly observed [8] ? To further motivate this work, a new argument pointing out a difficulty with the cosmological term that goes beyond the author’s earlier critique [9] is given in Section 2.
In Section 3, it is proposed that the novel approach to the “why now?” question is associated with the substantial increase in the volume of the expanding universe, particularly from 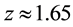 to
to , coupled with the corresponding reduction in density and temperature, causing it to condense into what is called “dark energy” which in the present model is a different thermodynamic phase of the dark matter, rather than a different type of substance. To be sure, this scenario does not explain why the dark matter parameters should have this property, or indeed why there is dark matter, rather than just baryonic matter, consequently, the term “approach” is used here rather than the term “answer”. In Section 4, it is proposed that the dark energy condensate reduces the speed of light, and hence behaves as though it has a non-electromagnetic index of refraction n. It is shown that the resulting reduction in the speed of light yields the equivalent of an added distance to the SNeIa, as if the universe were accelerating, and hence leads to their diminished brightness, or relative increase in apparent magnitude
, coupled with the corresponding reduction in density and temperature, causing it to condense into what is called “dark energy” which in the present model is a different thermodynamic phase of the dark matter, rather than a different type of substance. To be sure, this scenario does not explain why the dark matter parameters should have this property, or indeed why there is dark matter, rather than just baryonic matter, consequently, the term “approach” is used here rather than the term “answer”. In Section 4, it is proposed that the dark energy condensate reduces the speed of light, and hence behaves as though it has a non-electromagnetic index of refraction n. It is shown that the resulting reduction in the speed of light yields the equivalent of an added distance to the SNeIa, as if the universe were accelerating, and hence leads to their diminished brightness, or relative increase in apparent magnitude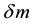 . An analytical expression for
. An analytical expression for  in terms of
in terms of 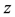 and n is derived. In Section 5, there is a description of how the curves for the distance modulus
and n is derived. In Section 5, there is a description of how the curves for the distance modulus 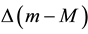 given in Tonry et al. [10] are used to obtain
given in Tonry et al. [10] are used to obtain 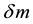 for the comparison between the accelerating universe for which one has
for the comparison between the accelerating universe for which one has ![]() and two different models with vanishing cosmological constant given by
and two different models with vanishing cosmological constant given by ![]() and the Einstein-de Sitter universe,
and the Einstein-de Sitter universe,![]()
![]() . This information is used to obtain a least squares fit for
. This information is used to obtain a least squares fit for ![]() for both cases, and a comparison of the results obtained for the theoretical value,
for both cases, and a comparison of the results obtained for the theoretical value,![]() . The differences of the distance moduli for the two non-accelerating models are given in Table 1 and Table 2, from which it emerges that the Einstein-de Sitter model is favored. It should be noted that the recent Planck satellite results [11] do not depart sufficiently from the fiducial values of
. The differences of the distance moduli for the two non-accelerating models are given in Table 1 and Table 2, from which it emerges that the Einstein-de Sitter model is favored. It should be noted that the recent Planck satellite results [11] do not depart sufficiently from the fiducial values of ![]() used here to merit any change in the following analysis. In Section 6, since baryon acoustic oscillations (BAO) favor the flat ΛCDM model, it is shown that the model can accommodate the BAO findings as well. The results are summarized in Table 3, and are in excellent agreement with Table 1. In Section 7, there is a discussion, and an empirical test of the model that would rule it out is suggested.
used here to merit any change in the following analysis. In Section 6, since baryon acoustic oscillations (BAO) favor the flat ΛCDM model, it is shown that the model can accommodate the BAO findings as well. The results are summarized in Table 3, and are in excellent agreement with Table 1. In Section 7, there is a discussion, and an empirical test of the model that would rule it out is suggested.
2. A Fundamental Difficulty with the Cosmological Term
As remarked in the Introduction, there is a difficulty with the cosmological term that was not discussed in the author’s previous critique [9] , and that further serves to justify seeking an alternative to the accelerating universe, at least one that employs the cosmological term. The difficulty is that the proper energy density associated with the cosmological term, ![]() , does not change as it acts together with the negative pressure,
, does not change as it acts together with the negative pressure, ![]() , associated with it as a source tensor in the field equations to accelerate the expansion of the universe. Thus, although the term does work, no work is done on it, or more generally stated, the cosmological term acts without being acted on. This is contrary to the general principle that emerged from Newton’s third law: if body A acts on body B, then body B acts on body A. To be sure, because of the relativistic correction to the instantaneous interaction envisaged in Newtonian physics, due to the finite speed of light, it well-known that the third law in its original form is no longer valid, but the principle in its less restrictive form as given above still remains valid: whatever acts gets acted on. There is no known exception to this generalized form of Newton’s third law in empirically established physics. Furthermore, the principle has predictive powers. For example, when one examines Newton’s definition of absolute time as flowing of itself, without regard to anything external, and takes into account that, as a consequence of the differential equations of classical dynamics, the flow of time acts to change the state of bodies while itself is not changed, and therefore acts without being acted on, one is led, following the principle, to conclude that absolute time cannot describe correctly the behavior of time in the physical world.
, associated with it as a source tensor in the field equations to accelerate the expansion of the universe. Thus, although the term does work, no work is done on it, or more generally stated, the cosmological term acts without being acted on. This is contrary to the general principle that emerged from Newton’s third law: if body A acts on body B, then body B acts on body A. To be sure, because of the relativistic correction to the instantaneous interaction envisaged in Newtonian physics, due to the finite speed of light, it well-known that the third law in its original form is no longer valid, but the principle in its less restrictive form as given above still remains valid: whatever acts gets acted on. There is no known exception to this generalized form of Newton’s third law in empirically established physics. Furthermore, the principle has predictive powers. For example, when one examines Newton’s definition of absolute time as flowing of itself, without regard to anything external, and takes into account that, as a consequence of the differential equations of classical dynamics, the flow of time acts to change the state of bodies while itself is not changed, and therefore acts without being acted on, one is led, following the principle, to conclude that absolute time cannot describe correctly the behavior of time in the physical world.
This inference is of course in agreement with what has been shown to be the case in relativity physics. Another example is furnished by the behavior of inertial mass: it acts to resist acceleration under the action of an external force. In Newtonian mechanics, inertial mass is a constant, and would act without being acted on; but according to the above principle that cannot be the case, and again from relativistic mechanics, it is well-known that inertial mass depends on velocity. To be sure, as has been widely discussed, quantum field theory, when supersymmetry is broken, or when the vacuum expectation value of the Higgs field is considered, yields an enormous value for the vacuum energy density, and hence for the cosmological constant; see, e.g., the recent books by Quigg [12] and Zee [13] , which contain numerous references to the literature. However, according to the above principle, this behavior of the vacuum energy density can only mean that quantum field theory is incomplete, as is already widely recognized, e.g., because of the large number of parameters it utilizes, and hence it is appropriate to infer that when the theory is complete, or at least when it is sufficiently complete, the vacuum energy density will be found to vanish, as it already does in unbroken supersymmetry [14] . This would not exclude small local changes in the zero-point energy of quantum fields, such as is the case in the Casimir effect [15] [16] for the electromagnetic field.
However, even if on the basis of the above critique one agrees with Einstein’s later view that the cosmological term does not belong in the field equations, this of course would not rule out the possibility that the universe is accelerating under the action of some other source, usually described as quintessence, whose energy-momen- tum tensor exhibits a negative pressure, and indeed, as is well-known, many such models are currently under study, see e.g., [17] [18] . However, none of these quintessence models have shown any compelling reason for their adoption, since they don’t address the apparent violation of the Copernican principle, and this is true as well of other more exotic models, such as those that propose a breakdown of the field equations. Consequently, it is reasonable to seek an alternative to the accelerating universe, as is done here.
3. Dark Energy, Dark Matter, Thermodynamics, and “Why Now?”
As emphasized in the Introduction, the “why now?” problem is fundamental, because of the apparent violation of the Copernican principle, as is widely recognized, and hence any solution to the diminished brightness of the SNeIa should provide an answer to this question. In this section, a novel approach to an eventual answer to this question will be given that, to be sure, does not explain why the universe is accelerating now, but rather why the universe appears to be accelerating now, even though, as is claimed here, it is actually decelerating. The trial idea is as follows: when the universe expanded, say from red-shift z =1 to z = 0, for which the central region exhibits the greatest diminution of brightness, since the expansion parameter for an FLRW expanding universe satisfies
![]() (1)
(1)
where ![]() is the expansion parameter at the present epoch, the volume of the universe increased by a factor of 8. Note that for a spherical universe, the volume is
is the expansion parameter at the present epoch, the volume of the universe increased by a factor of 8. Note that for a spherical universe, the volume is![]() , while for the flat universe, favored by inflation, since the observed universe occupies only a small portion of the otherwise infinite space, depending on the shape of the observed universe, its volume would be of the form
, while for the flat universe, favored by inflation, since the observed universe occupies only a small portion of the otherwise infinite space, depending on the shape of the observed universe, its volume would be of the form![]() , and in the simplest case,
, and in the simplest case, ![]() , so that for both cases, closed and flat, the volume behaves as
, so that for both cases, closed and flat, the volume behaves as![]() . To be sure, one can get the same volumetric expansion as above by choosing other pairs of values of z, e.g., from z = 5 to z = 2, or from z =11 to z = 5. However, the density and temperature of the dark matter in these latter cases is greater than for the smaller values of z. So it will be assumed that the density and temperature of the dark matter in the intergalactic space (IGS) are the critical parameters for the assumption that follows, as well as the volume increase; the density and temperature being of course related to the volume increase by the unknown equation of state. Also, since from [8] , the apparent magnitude at z = 1.65 ± 0.15 of a Type Ia supernova is observed as being from a universe that was not accelerating, while from observation as given in Figure 9 of [10] , the increase in apparent magnitude reaches its peak near
. To be sure, one can get the same volumetric expansion as above by choosing other pairs of values of z, e.g., from z = 5 to z = 2, or from z =11 to z = 5. However, the density and temperature of the dark matter in these latter cases is greater than for the smaller values of z. So it will be assumed that the density and temperature of the dark matter in the intergalactic space (IGS) are the critical parameters for the assumption that follows, as well as the volume increase; the density and temperature being of course related to the volume increase by the unknown equation of state. Also, since from [8] , the apparent magnitude at z = 1.65 ± 0.15 of a Type Ia supernova is observed as being from a universe that was not accelerating, while from observation as given in Figure 9 of [10] , the increase in apparent magnitude reaches its peak near![]() , the assumed effect described below would take place as a consequence of a volume increase of about 5.5, somewhat less than the trial value. Next, assume that for these higher values of z, say z > 1.65, there is negligible density of dark energy, and that apart from baryonic matter, Cosmic Microwave Background (CMB), and neutrino background, there is only dark matter. Further, assume that associated with the substantial increase in volume from
, the assumed effect described below would take place as a consequence of a volume increase of about 5.5, somewhat less than the trial value. Next, assume that for these higher values of z, say z > 1.65, there is negligible density of dark energy, and that apart from baryonic matter, Cosmic Microwave Background (CMB), and neutrino background, there is only dark matter. Further, assume that associated with the substantial increase in volume from ![]() to
to![]() , in a possible analogy with the case for suitable types of baryonic gases that exhibit expansion-cooling due to the Joule-Thomson effect, the dark matter for sufficiently low density and temperature also exhibits expansion-cooling, although the mechanism is left open. Then, under these circumstances, the dark matter would condense, and the resulting product would be the dark energy. Since the dark energy condensate would have a greater density than the dark matter from which it formed, in order to conserve mass, the dark energy would possibly be in the form of globules whose sizes and spatial distribution are left undetermined. Needless to say, this scenario in which dark energy is a condensed form of dark matter will require considerable further investigation that is well beyond the scope of this work, which is to show that with a suitable assumption about the propagation of light through the dark energy, the diminished brightness of the high redshift SNeIa can be explained.
, in a possible analogy with the case for suitable types of baryonic gases that exhibit expansion-cooling due to the Joule-Thomson effect, the dark matter for sufficiently low density and temperature also exhibits expansion-cooling, although the mechanism is left open. Then, under these circumstances, the dark matter would condense, and the resulting product would be the dark energy. Since the dark energy condensate would have a greater density than the dark matter from which it formed, in order to conserve mass, the dark energy would possibly be in the form of globules whose sizes and spatial distribution are left undetermined. Needless to say, this scenario in which dark energy is a condensed form of dark matter will require considerable further investigation that is well beyond the scope of this work, which is to show that with a suitable assumption about the propagation of light through the dark energy, the diminished brightness of the high redshift SNeIa can be explained.
It will be assumed in keeping with the findings of the SNeIa investigators, that the dark energy is non-disper- sive, and obviously transparent; however, unlike what has been assumed in the SNeIa studies, the dark energy will have an unexpected property when it comes to the propagation of light, namely: it will reduce the speed of light from its vacuum speed by a significant amount, as described in the next section. This assumed property is in contrast to the standard model of dark energy for the accelerating universe, which associates its energy-mo- mentum tensor with a negative pressure, such as in the cosmological term, but does not assume an influence on the speed of light. Also, it should be pointed out, that although in the ![]() model, one refers to the dark matter as “cold”, this is a relative term, and in this model it should be understood to mean that the kinetic energy density associated with the dark matter is not zero, but negligible compared to its energy density, so that the dark energy can be even colder, and the assumed expansion-cooling and condensation can take place. Clearly the cold dark matter used here is somewhat warm, but quantitatively how warm is an issue this scenario is still too qualitative to address. Also, since in the expanding universe it is only the space between the galaxies that expands, not the galaxies themselves, because of the strong gravitational binding pseudo-forces within the galaxies that are able to counteract the expansion of space locally, it follows that the dark matter in the galaxies is not condensed, and the speed of light when going through the dark matter in the galaxies is the vacuum speed c. Also there should not be any corrections to gravitational lensing, under suitable approximations, because of the lower light speed when light is traveling well outside the galaxies as is shown at the end of the next section. On the other hand, for light traveling through the galactic halos there would be a counteracting influence on gravitational lensing, since the light would experience a transition from a lower speed in the IGS to a range of higher speeds in the halos; this would act as a diverging lens, and tend to cancel the weaker gravitational attractive deflection of light that acts as a converging lens. This diverging lens prediction is left to future more detailed studies to see whether or not there is such an effect that could serve as a test of the model. As a further simplification, since the sizes of the galaxies are so much smaller than the cosmic distances light travels to the observer from the SNeIa, the correction for return to the vacuum speed of light c in the Galaxy will be ignored. However, importantly, this return to vacuum speed means that measurements made within the Galaxy that involve the speed of light have not been affected by the assumed slowing down of light traveling through the dark energy in the IGS. To be sure, the assumption made here that the vacuum speed of light within the galaxies is c, while in agreement with current astronomical practice, is one that should be further tested through suitable observations.
model, one refers to the dark matter as “cold”, this is a relative term, and in this model it should be understood to mean that the kinetic energy density associated with the dark matter is not zero, but negligible compared to its energy density, so that the dark energy can be even colder, and the assumed expansion-cooling and condensation can take place. Clearly the cold dark matter used here is somewhat warm, but quantitatively how warm is an issue this scenario is still too qualitative to address. Also, since in the expanding universe it is only the space between the galaxies that expands, not the galaxies themselves, because of the strong gravitational binding pseudo-forces within the galaxies that are able to counteract the expansion of space locally, it follows that the dark matter in the galaxies is not condensed, and the speed of light when going through the dark matter in the galaxies is the vacuum speed c. Also there should not be any corrections to gravitational lensing, under suitable approximations, because of the lower light speed when light is traveling well outside the galaxies as is shown at the end of the next section. On the other hand, for light traveling through the galactic halos there would be a counteracting influence on gravitational lensing, since the light would experience a transition from a lower speed in the IGS to a range of higher speeds in the halos; this would act as a diverging lens, and tend to cancel the weaker gravitational attractive deflection of light that acts as a converging lens. This diverging lens prediction is left to future more detailed studies to see whether or not there is such an effect that could serve as a test of the model. As a further simplification, since the sizes of the galaxies are so much smaller than the cosmic distances light travels to the observer from the SNeIa, the correction for return to the vacuum speed of light c in the Galaxy will be ignored. However, importantly, this return to vacuum speed means that measurements made within the Galaxy that involve the speed of light have not been affected by the assumed slowing down of light traveling through the dark energy in the IGS. To be sure, the assumption made here that the vacuum speed of light within the galaxies is c, while in agreement with current astronomical practice, is one that should be further tested through suitable observations.
4. Slowing Down of Light by Dark Energy, and the Effect on Apparent Magnitude
To describe the postulated slowing down of light by dark energy, a non-electromagnetic index of refraction n will be introduced. Since it has also been assumed that the dark energy formed from the expansion-cooling of the dark matter, and since this process obviously takes time, for sufficiently high z the index n must be close to unity, and hence n evolves. However, in the analysis below, n is taken to be a constant, and the failure to include the evolution of n will show up in a comparison of theory with the curve that describe the accelerating universe, so that the simplified model will yield an increase in apparent magnitude beyond what is observed as one approaches![]() . The description of the refraction has been characterized above as “non-electromagnetic”, since, unlike ordinary refraction by a baryonic medium that is based on the electromagnetic interaction between light and the electrically polarizable medium, the reduction in the speed of light caused by the interaction of light with the dark energy does not give rise to Cherenkov radiation for the high-energy cosmic-ray charged particles traveling through the dark energy faster than
. The description of the refraction has been characterized above as “non-electromagnetic”, since, unlike ordinary refraction by a baryonic medium that is based on the electromagnetic interaction between light and the electrically polarizable medium, the reduction in the speed of light caused by the interaction of light with the dark energy does not give rise to Cherenkov radiation for the high-energy cosmic-ray charged particles traveling through the dark energy faster than![]() . This scenario will require that the particles making up the dark energy are electrically neutral, and hence that the dark energy is not an electrically polarizable medium. On the other hand, since the photons will have to interact with the dark energy in order that their speed be reduced to
. This scenario will require that the particles making up the dark energy are electrically neutral, and hence that the dark energy is not an electrically polarizable medium. On the other hand, since the photons will have to interact with the dark energy in order that their speed be reduced to![]() , there will have to be some new kind of interaction between photons and dark energy that is not of an electromagnetic nature, and furthermore is negligible for dark matter. The mathematical form of this interaction is left open here, but it would be gauge invariant, and presumably involve coupling with the photon’s spin.
, there will have to be some new kind of interaction between photons and dark energy that is not of an electromagnetic nature, and furthermore is negligible for dark matter. The mathematical form of this interaction is left open here, but it would be gauge invariant, and presumably involve coupling with the photon’s spin.
To derive the effect on apparent magnitude due to the slowing down of light, one first obtains the extra amount of time ![]() it takes light to travel a distance
it takes light to travel a distance ![]() through the dark energy compared with that through the vacuum, that through the dark energy being
through the dark energy compared with that through the vacuum, that through the dark energy being![]() , and that through the vacuum being
, and that through the vacuum being![]() . Hence, one has
. Hence, one has![]() . Since the universe is expanding,
. Since the universe is expanding, ![]() , and hence the universe will expand by the extra amount
, and hence the universe will expand by the extra amount
![]() (2)
(2)
beyond what it would have expanded if ![]() The fractional expansion is given by
The fractional expansion is given by
![]() (3)
(3)
and this expression is to be integrated from the emission time to the present. But since it is red shift that is measured, it is desirable to convert this relation from one that is in terms of the time to one that is in terms of red-shift. Now from (1), ![]() , so that
, so that![]() , and the integral becomes
, and the integral becomes
![]() (4)
(4)
The standard expression for the flux F at the observer in terms of the luminosity ![]() and the luminosity distance DL is given by
and the luminosity distance DL is given by![]() . Hence, since the actual luminosity distance
. Hence, since the actual luminosity distance ![]() has been increased by the factor
has been increased by the factor![]() , one has
, one has
![]() (5)
(5)
and the resulting reduced observed flux ![]() is given by
is given by
![]() (6)
(6)
Consequently, since the apparent magnitude is![]() , it follows from (6) one has that
, it follows from (6) one has that
![]() . (7)
. (7)
with the second term on the right hand side being the increase in apparent magnitude ![]() due to the slowing down of light, and the resulting additional expansion, and hence removing the square in the argument for the log, it is given by
due to the slowing down of light, and the resulting additional expansion, and hence removing the square in the argument for the log, it is given by
![]() (8)
(8)
This equation is the basic finding of the model. In the next section, a least squares determination of ![]() is made, and comparison with the accelerating model given for two different decelerating models. This can be done, because as is clear from the above derivation, (8) does not depend on the particular expanding model that is being employed, but only that (1) holds, hence comparison could have been made, e.g., with a closed universe.
is made, and comparison with the accelerating model given for two different decelerating models. This can be done, because as is clear from the above derivation, (8) does not depend on the particular expanding model that is being employed, but only that (1) holds, hence comparison could have been made, e.g., with a closed universe.
It was noted in Section 3 that light, when traveling through the dark energy, well outside the lensing galaxies, travels at a speed less than c, and given here as![]() , should experience the same gravitational lensing as if it were traveling with speed c. To show this, note that in the asymptotic region, far from the lensing galaxy, but not so far that one has to take into account the time dependence of the expanding universe, to a first approximation the path of the light through the dark energy in the IGS is along the space-time null geodesic
, should experience the same gravitational lensing as if it were traveling with speed c. To show this, note that in the asymptotic region, far from the lensing galaxy, but not so far that one has to take into account the time dependence of the expanding universe, to a first approximation the path of the light through the dark energy in the IGS is along the space-time null geodesic![]() , where
, where![]() , and where
, and where ![]() is the Minkowski metric, and importantly, where
is the Minkowski metric, and importantly, where![]() , instead of
, instead of ![]() However, more exactly, the line element is
However, more exactly, the line element is ![]() with
with![]() , and where the
, and where the ![]() are the gravitational corrections to the metric due to the lensing galaxy, with
are the gravitational corrections to the metric due to the lensing galaxy, with ![]() in the asymptotic region. To the extent one can treat the lensing galaxy as static, the
in the asymptotic region. To the extent one can treat the lensing galaxy as static, the ![]() are time-independent,
are time-independent,![]() . Hence, since the gravitational deflection of light is due to the
. Hence, since the gravitational deflection of light is due to the![]() , at the above level of approximation, the lensing is independent of the light’s reduced speed.
, at the above level of approximation, the lensing is independent of the light’s reduced speed.
5. Determination of n
As described in the Introduction, the determination of n will be based on the curves of the distance moduli ![]() versus z given in Tonry et al. [10] ; there in Figure 8, in which the fall 1999 data points for SNeIa are highlighted, three curves are shown for
versus z given in Tonry et al. [10] ; there in Figure 8, in which the fall 1999 data points for SNeIa are highlighted, three curves are shown for ![]() that are given in a residual Hubble diagram for an empty universe in which the upper curve (a) is for
that are given in a residual Hubble diagram for an empty universe in which the upper curve (a) is for![]() , and the next curve lower down (b) is for
, and the next curve lower down (b) is for![]() , and further down (c), the Einstein-de Sitter universe, for which
, and further down (c), the Einstein-de Sitter universe, for which![]() . Although there is a great deal of scatter for the data points, the generally accepted view is that the uppermost curve (a) that ranges at
. Although there is a great deal of scatter for the data points, the generally accepted view is that the uppermost curve (a) that ranges at ![]() from
from ![]() to a maximum near
to a maximum near ![]() of
of![]() , and descends to a value of
, and descends to a value of ![]() at z = 1, that describes an accelerating universe, is the observationally preferred description over the two lower curves, (b) and (c). The middle curve (b) ranges for the values z = 0, 0.5, 1.0, from
at z = 1, that describes an accelerating universe, is the observationally preferred description over the two lower curves, (b) and (c). The middle curve (b) ranges for the values z = 0, 0.5, 1.0, from ![]() to −0.09, and then to −0.20 respectively, while the third curve (c), which will be shown to be of greater interest here, ranges
to −0.09, and then to −0.20 respectively, while the third curve (c), which will be shown to be of greater interest here, ranges ![]() respectively.
respectively.
The way these curves will be used to determine n is as follows: the difference between the distance moduli for the curve (a) and the two lower curves will be taken for the range of z from 0.10 to 1.0 as give in Table 1 and Table 2. (The differences were obtained by enlarging Figure 8, and measuring the difference between the two curves with a pair of dividers, and further subdividing the scale given in units of 0.1 mag by a factor of sixteen.) In taking the difference, the M correction to the distance moduli cancels out, so one has that ![]() , and also that
, and also that![]() , are independent of
, are independent of![]() . Because of the greater interest in the Einstein-de Sitter universe (c), the latter differences will be given first in Table 1, and used in conjunction with (8) to obtain a least squares fit to (n − 1). One finds,
. Because of the greater interest in the Einstein-de Sitter universe (c), the latter differences will be given first in Table 1, and used in conjunction with (8) to obtain a least squares fit to (n − 1). One finds, ![]() , and hence
, and hence![]() , a surprisingly large value. The least squares value of n − 1 can now be used in conjunction with (8) to obtain a theoretical value for the apparent magnitude difference, denoted in the third column of Table 1 by
, a surprisingly large value. The least squares value of n − 1 can now be used in conjunction with (8) to obtain a theoretical value for the apparent magnitude difference, denoted in the third column of Table 1 by ![]() for the different values of z. In the fourth column, labeled “
for the different values of z. In the fourth column, labeled “![]() ”, one has
”, one has ![]() In the last column, the ratio
In the last column, the ratio ![]() is given as a percentage. Note that for z = 0.1, in order to avoid excessive and possibly misleading round-off error, three places after the decimal point are used in columns 2 - 4. In Table 2, with three places after the decimal point being used for z = 0.1, 0.2, the same results as above for the
is given as a percentage. Note that for z = 0.1, in order to avoid excessive and possibly misleading round-off error, three places after the decimal point are used in columns 2 - 4. In Table 2, with three places after the decimal point being used for z = 0.1, 0.2, the same results as above for the ![]() universe are shown for comparison. The least squares value for
universe are shown for comparison. The least squares value for ![]() was found to be 0.26, and hence
was found to be 0.26, and hence![]() . It is clear that the fit in Table 2 is poor, by comparison with the results in Table 1, as should be the case, since it is known from the studies of the CMB that the total
. It is clear that the fit in Table 2 is poor, by comparison with the results in Table 1, as should be the case, since it is known from the studies of the CMB that the total ![]() is very close to unity, and hence if the proposed model is on the right track, it should disfavor this low
is very close to unity, and hence if the proposed model is on the right track, it should disfavor this low ![]() model of the universe, which it does.
model of the universe, which it does.
6. Baryon Acoustic Oscillations
Although the above analysis shows that the reduction of light speed through the dark energy can provide an alternative explanation for the diminished brightness of the SNeIa, the question arises whether the proposed model can also accommodate the findings from the study of baryon acoustic oscillations (BAO), that have been shown to be consistently described by the flat ΛCDM model [19] ? Outside the scope of the work here is the BAO work itself, that provides new determinations of cosmological parameters, see e.g. [20] , and, significantly, provides a “standard ruler” [21] in the range of redshifts of interest here. In the simple flat space model being used here, if the ruler is transversely oriented with a width ![]() and subtends an angle
and subtends an angle![]() , then the angular diameter distance is given by
, then the angular diameter distance is given by![]() , and from distance duality [22] , the luminosity distance is given by
, and from distance duality [22] , the luminosity distance is given by![]() . In what follows, expressions will be obtained for
. In what follows, expressions will be obtained for![]() , and hence
, and hence![]() , for the two flat space models:
, for the two flat space models: ![]() and
and![]() , and it will be shown that the ratio of the two values for
, and it will be shown that the ratio of the two values for ![]() agrees with the fractional distance increase predicted by reduction of light speed model, and hence it is in complete agreement with the results already found for the diminished brightness of the SNeIa.
agrees with the fractional distance increase predicted by reduction of light speed model, and hence it is in complete agreement with the results already found for the diminished brightness of the SNeIa.
The following derivation is standard in the literature, and is given for completeness, and to deal specifically with the particular case considered here, in which the only two source terms in Einstein’s field equations are the CDM tensor, and the cosmological term.
From the FLRW flat space-time element, ![]() , for the Einstein field equation
, for the Einstein field equation![]() ,
, ![]() , and
, and![]() , one has
, one has
![]() (9)
(9)
where ![]() is the CDM mass density. From (9) one has
is the CDM mass density. From (9) one has
![]() (10)
(10)
where ![]() is the Hubble parameter, and H0 is its value at the present epoch.
is the Hubble parameter, and H0 is its value at the present epoch.
Since ![]() from the fact that the “cold” matter tensor obeys the energy conservation law, since pressure, i.e., kinetic energy, is ignored, one has from (1) that
from the fact that the “cold” matter tensor obeys the energy conservation law, since pressure, i.e., kinetic energy, is ignored, one has from (1) that![]() . Also, with
. Also, with![]() ,
, ![]() , and with
, and with ![]() and
and![]() , (10) can be rewritten as a function of z rather than time as follows
, (10) can be rewritten as a function of z rather than time as follows
![]() (11)
(11)
Following standard notation, introducing the definition, ![]() , (11) can be written as
, (11) can be written as
![]() (12)
(12)
Since in these models light travels along a null geodesic, ![]() , one has that
, one has that![]() , and hence
, and hence
![]() (13)
(13)
Once again, upon making use of (1), and integrating the left hand side of (13), one has
![]() (14)
(14)
Note that some authors effectively set![]() , and their “r” has the dimensions of a length, in contrast with the usage here, for which “r” is dimensionless.
, and their “r” has the dimensions of a length, in contrast with the usage here, for which “r” is dimensionless.
The angular distance for flat space is![]() , and for the luminosity distance one has
, and for the luminosity distance one has ![]()
![]() Now for the ΛCDM model, one obtains a value for
Now for the ΛCDM model, one obtains a value for ![]() from (14) given by
from (14) given by![]() , and likewise for the Einstein-de Sitter model one obtains another value for
, and likewise for the Einstein-de Sitter model one obtains another value for ![]() given by
given by![]() . Taking the ratio of either
. Taking the ratio of either![]() , or
, or![]() , the quantities
, the quantities ![]() and
and ![]() cancel, and hence introducing
cancel, and hence introducing ![]() defined as
defined as
![]() (15)
(15)
both ratios reduce to![]() . The claim of this work is that because of the effective increase in distance,
. The claim of this work is that because of the effective increase in distance, ![]() , so that taking logs, one should have that
, so that taking logs, one should have that
![]() (16)
(16)
Thus, to within a factor of five, since one is comparing distance here rather than apparent magnitude, the difference should be equal to that found in Section 3 for![]() . Upon setting
. Upon setting![]() , and
, and![]() , the integral for
, the integral for ![]() is given by
is given by
![]() (17)
(17)
which has to be evaluated numerically. On the other hand, for the Einstein-de Sitter model, one has![]() ,
, ![]() , and the integral for
, and the integral for ![]() is readily evaluated and given by
is readily evaluated and given by
![]() (18)
(18)
The check of the validity of (16), for the same range of ![]() as before, is given in Table 3 below, where it is clear that, to within the factor of five, and the allowance for small rounding-off errors, the agreement with the results in Table 1 is excellent. Note that once again, to lessen the round-off error for z = 0.1, four places after the decimal point have been used in columns 2 - 4. Thus the BAO observations, as was found above for the SNeIa observations, can be explained alternatively as due to the slowing down of light, rather than due to the acceleration of the universe. This is most likely true of other proposed methods for establishing an accelerating universe, but it is left to future investigations to determine whether this is in fact the case.
as before, is given in Table 3 below, where it is clear that, to within the factor of five, and the allowance for small rounding-off errors, the agreement with the results in Table 1 is excellent. Note that once again, to lessen the round-off error for z = 0.1, four places after the decimal point have been used in columns 2 - 4. Thus the BAO observations, as was found above for the SNeIa observations, can be explained alternatively as due to the slowing down of light, rather than due to the acceleration of the universe. This is most likely true of other proposed methods for establishing an accelerating universe, but it is left to future investigations to determine whether this is in fact the case.
7. Discussion
It is clear from Table 1 and Table 3 that the proposed model provides a very good fit to the accelerating model for the range![]() , since the error in Table 1 ranges from −3.7% at z = 0.3 to 3.8% at z = 0.8, while from Table 3, it ranges from −3.6% at z = 0.3 to 2.8% at z = 0.8. Also the model gives an excellent fit for the more restricted range,
, since the error in Table 1 ranges from −3.7% at z = 0.3 to 3.8% at z = 0.8, while from Table 3, it ranges from −3.6% at z = 0.3 to 2.8% at z = 0.8. Also the model gives an excellent fit for the more restricted range, ![]() , since for Table 1 one has −2.9% at z = 0.4 to 2.0% at z = 0.7, while for Table 3 one has −2.9% at z = 0.4 to 1.0% at z = 0.7. For the range
, since for Table 1 one has −2.9% at z = 0.4 to 2.0% at z = 0.7, while for Table 3 one has −2.9% at z = 0.4 to 1.0% at z = 0.7. For the range![]() , the fit from both Tables becomes somewhat poorer, and this can be explained as due to the possibility that the postulated condensation of
, the fit from both Tables becomes somewhat poorer, and this can be explained as due to the possibility that the postulated condensation of
the dark matter into dark energy in the IGS is incomplete, and that the index of refraction ![]() is no longer constant, but approaches unity as one goes to higher redshifts, which the present model does not take into account. On the other hand, the fact that the magnitude of the percent of disagreement steadily increases from 2.9 percent at z = 0.4 for both Tables, to ~6.5 percent at z = 0.1, after averaging the values from the two Tables, undoubtedly represents an increasing disagreement with the
is no longer constant, but approaches unity as one goes to higher redshifts, which the present model does not take into account. On the other hand, the fact that the magnitude of the percent of disagreement steadily increases from 2.9 percent at z = 0.4 for both Tables, to ~6.5 percent at z = 0.1, after averaging the values from the two Tables, undoubtedly represents an increasing disagreement with the ![]() model for lower z. Although this continues as one goes to z < 0.1, it eventually starts to diminish since
model for lower z. Although this continues as one goes to z < 0.1, it eventually starts to diminish since ![]() vanishes for z = 0, and hence the disagreement between the two models vanishes at z = 0, as it must. Thus there is a value of z where the magnitude of the percentage of disagreement between the two models is a maximum, and this was found to be about 6.4% in the neighborhood of z = 0.03, by the same calculation that led to Table 3. Thus there is a systematic trend for the model to estimate the SNeIa to be slightly brighter in this lower z range than is predicted by the
vanishes for z = 0, and hence the disagreement between the two models vanishes at z = 0, as it must. Thus there is a value of z where the magnitude of the percentage of disagreement between the two models is a maximum, and this was found to be about 6.4% in the neighborhood of z = 0.03, by the same calculation that led to Table 3. Thus there is a systematic trend for the model to estimate the SNeIa to be slightly brighter in this lower z range than is predicted by the ![]() model, which may eventually prove to be helpful in deciding between the two models. Although the large scatter in the data at these lower values of z, and the uncertainties in median values ranging almost to 0.05 mag, as shown in Figure 9 in the above cited article of Tonry et al. [10] , and discussed there, make it difficult to see how one could prefer one model over the other in this range of redshifts, since from Table 1 for z = 0.1, the magnitude of the difference in apparent magnitude between the two models is only 0.007 mag.
model, which may eventually prove to be helpful in deciding between the two models. Although the large scatter in the data at these lower values of z, and the uncertainties in median values ranging almost to 0.05 mag, as shown in Figure 9 in the above cited article of Tonry et al. [10] , and discussed there, make it difficult to see how one could prefer one model over the other in this range of redshifts, since from Table 1 for z = 0.1, the magnitude of the difference in apparent magnitude between the two models is only 0.007 mag.
However, undoubtedly, the main challenges for the model are: 1) to explain theoretically how the non-electro- magnetic interaction of light with the dark energy could possibly give rise to such a substantial slowing down of light that its speed is reduced to approximately two-thirds its vacuum speed, and to see whether this proposed interaction predicts dispersion, which could lead to measurably different arrival times for visible light and X-rays and gamma rays; 2) to describe analytically the condensation phase transition of dark matter into dark energy, and to show that it is complete by![]() , and possibly somewhat earlier, with a corresponding smaller volume increase than the above approximate factor of 5.5; and 3) to extend the analysis that led to (8) to the redshift range, say,
, and possibly somewhat earlier, with a corresponding smaller volume increase than the above approximate factor of 5.5; and 3) to extend the analysis that led to (8) to the redshift range, say, ![]() so as to allow for n tending to unity as one goes to higher redshifts. Despite these challenges, there would appear to be excellent agreement with the BAO studies [19] , because their recent distance measurement is for galaxies with an effective redshift z = 0.57, and this is precisely the redshift region where the present model, as indicated in Table 1, is in excellent agreement with the accelerating flat
so as to allow for n tending to unity as one goes to higher redshifts. Despite these challenges, there would appear to be excellent agreement with the BAO studies [19] , because their recent distance measurement is for galaxies with an effective redshift z = 0.57, and this is precisely the redshift region where the present model, as indicated in Table 1, is in excellent agreement with the accelerating flat ![]() model for the increased magnitude of the SNeIa, and hence in agreement for the distances to the supernovae, as corroborated by Table 3, since on account of the slowing down of light, the distances in the proposed model are increased over the non-accelerating model distances according to (5). Thus, since the BAO studies in this redshift range agree with the flat
model for the increased magnitude of the SNeIa, and hence in agreement for the distances to the supernovae, as corroborated by Table 3, since on account of the slowing down of light, the distances in the proposed model are increased over the non-accelerating model distances according to (5). Thus, since the BAO studies in this redshift range agree with the flat ![]() cosmology, they also agree with the present model as well.
cosmology, they also agree with the present model as well.
In conclusion, although the proposed model is not without challenges, it has the advantage that it gives a new approach to the fundamental “why now?” question, that left unanswered would undermine the Copernican principle. Also, importantly, as pointed out in Section 2, the model, in contrast with the ![]() model, avoids a conflict with a fundamental principle, based on a generalization of Newton’s third law, that rules out the cosmological term. In addition, the model unites the dark matter and dark energy as two states of the same substance, instead of making use of two totally unrelated substances, as in the present accelerating model. Finally, the model suggests a new investigation to supplement programs to investigate dark energy, such as that prepared at Fermilab [23] : there should be attempts made to determine the speed of light in the intergalactic regions of space, as well as in the outermost halo regions of the galaxies. Obviously, if such measurements showed that the speed of light is indeed
model, avoids a conflict with a fundamental principle, based on a generalization of Newton’s third law, that rules out the cosmological term. In addition, the model unites the dark matter and dark energy as two states of the same substance, instead of making use of two totally unrelated substances, as in the present accelerating model. Finally, the model suggests a new investigation to supplement programs to investigate dark energy, such as that prepared at Fermilab [23] : there should be attempts made to determine the speed of light in the intergalactic regions of space, as well as in the outermost halo regions of the galaxies. Obviously, if such measurements showed that the speed of light is indeed ![]() in these regions, this would rule out the model proposed here, and lend further support to the accelerating universe.
in these regions, this would rule out the model proposed here, and lend further support to the accelerating universe.
References
- Perlmutter, S., et al. (1998) Nature, 391, 51-54. (Erratum, 392, 311).
- Perlmutter, S., et al. (1999) Astrophysical Journal, 517, 565-586. http://dx.doi.org/10.1086/307221
- Riess, A., et al. (1998) Astronomical Journal, 116, 1009-1038. http://dx.doi.org/10.1086/300499
- Schmidt, B., et al. (1998) Astrophysical Journal, 507, 46-63. http://dx.doi.org/10.1086/306308
- Riess, A., et al. (2000) Astrophysical Journal, 536, 62-67. http://dx.doi.org/10.1086/308939
- Bondi, H. (1952) Cosmology. Cambridge University Press, Cambridge, 13.
- Uzan, J.-P. (2010) Dark Energy, Gravitation, and the Copernican principle. In: Ruiz-Lapuente, P., Ed., Dark Energy, Cambridge University Press, Cambridge, 5-6. http://dx.doi.org/10.1017/CBO9781139193627.002
- Riess, A., et al. (2001) Astrophysical Journal, 560, 49-71. http://dx.doi.org/10.1086/322348
- Tangherlini, F.R. (1991) Nuovo Cimento B, 106, 123-146.
- Tonry, J.L., et al. (2003) Astrophysical Journal, 594. 1-24. http://dx.doi.org/10.1086/376865
- Ade, P.A.R., Aghanim, N., Arnaud, M., et al. (2014) Astronomy and Astrophysics, 571, 66 p.
- Quigg, C. (2013) Gauge Theories of the Strong, Weak, and Electromagnetic Interactions. 2nd Edition, Princeton University Press, Princeton, 246-247.
- Zee, A. (2010) Quantum Field Theory in a Nutshell. 2nd Edition, Princeton University Press, Princeton, 448-451.
- Wess, J. and Zumino, B. (1974) Nuclear Physics B, 70, 39-50. http://dx.doi.org/10.1016/0550-3213(74)90355-1
- Casimir, H.B.G. (1948) Proceedings of the Royal Netherlands Academy of Arts and Sciences Series B, 51, 793-795.
- Lamoreaux, S.K. (1997) Physical Review Letters, 78, 5-8. http://dx.doi.org/10.1103/PhysRevLett.78.5
- Amendola, L. and Tsujikawa, S. (2010) Dark Energy. Cambridge University Press, Cambridge, 134-295.
- Wang, Y. (2010) Dark Energy, Wiley-VCH, Verlag GmbH & Co, KGaA, Weinheim, 34-49.
- Anderson, L., et al. (2011) Monthly Notices of the Royal Astronomical Society, 000, 2-33.
- Eisenstein, D.J., Zehavi, I., Hogg, D.W., Scoccimarro, R., Blanton, M.R., Nichol, R.C., et al. (2005) Astrophysical Journal, 633, 560-574. http://dx.doi.org/10.1086/466512
- Cooray, A., Hu, W., Huterer, D. and Jeffre, M. (2001) Astrophysical Journal, 557, L7-L10. http://dx.doi.org/10.1086/323323
- Etherington, I.M.H. (2007) General Relativity and Gravitation, 39, 1055-1067. http://dx.doi.org/10.1080/14786443309462220
- Kolb, R. (2006) Report of the Dark Energy Task Force. Fermi National Accelerator Laboratory, Batavia, IL, 1-123.



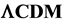 model from baryon acoustic oscillations (BAO) studies can also be accommodated by the model. Two tables are given to compare the model with apparent magnitude differences and length differences between the flat
model from baryon acoustic oscillations (BAO) studies can also be accommodated by the model. Two tables are given to compare the model with apparent magnitude differences and length differences between the flat 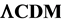 universe and the Einstein-de Sitter universe, and they show that the model yields these differences quite accurately. A third table comparing the apparent magnitude difference between
universe and the Einstein-de Sitter universe, and they show that the model yields these differences quite accurately. A third table comparing the apparent magnitude difference between 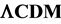 and a universe with
and a universe with  and
and 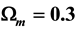 is also given. It exhibits poor agreement with
is also given. It exhibits poor agreement with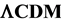 , and hence the model favors the need for dark ener- gy, albeit without negative pressure. As a new approach to the “why now?” problem, and its apparent challenge to the Copernican principle, it is proposed that dark energy is a condensed form of dark matter caused by expansion cooling, rather than a different substance. A motivation for an alternative to
, and hence the model favors the need for dark ener- gy, albeit without negative pressure. As a new approach to the “why now?” problem, and its apparent challenge to the Copernican principle, it is proposed that dark energy is a condensed form of dark matter caused by expansion cooling, rather than a different substance. A motivation for an alternative to  is presented based on a principle that rules out the cosmological term.
is presented based on a principle that rules out the cosmological term.
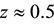 , rather than at, say,
, rather than at, say,  , where the expected brightness of a Type Ia supernova for a decelerating universe is possibly observed [8] ? To further motivate this work, a new argument pointing out a difficulty with the cosmological term that goes beyond the author’s earlier critique [9] is given in Section 2.
, where the expected brightness of a Type Ia supernova for a decelerating universe is possibly observed [8] ? To further motivate this work, a new argument pointing out a difficulty with the cosmological term that goes beyond the author’s earlier critique [9] is given in Section 2.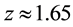 to
to , coupled with the corresponding reduction in density and temperature, causing it to condense into what is called “dark energy” which in the present model is a different thermodynamic phase of the dark matter, rather than a different type of substance. To be sure, this scenario does not explain why the dark matter parameters should have this property, or indeed why there is dark matter, rather than just baryonic matter, consequently, the term “approach” is used here rather than the term “answer”. In Section 4, it is proposed that the dark energy condensate reduces the speed of light, and hence behaves as though it has a non-electromagnetic index of refraction n. It is shown that the resulting reduction in the speed of light yields the equivalent of an added distance to the SNeIa, as if the universe were accelerating, and hence leads to their diminished brightness, or relative increase in apparent magnitude
, coupled with the corresponding reduction in density and temperature, causing it to condense into what is called “dark energy” which in the present model is a different thermodynamic phase of the dark matter, rather than a different type of substance. To be sure, this scenario does not explain why the dark matter parameters should have this property, or indeed why there is dark matter, rather than just baryonic matter, consequently, the term “approach” is used here rather than the term “answer”. In Section 4, it is proposed that the dark energy condensate reduces the speed of light, and hence behaves as though it has a non-electromagnetic index of refraction n. It is shown that the resulting reduction in the speed of light yields the equivalent of an added distance to the SNeIa, as if the universe were accelerating, and hence leads to their diminished brightness, or relative increase in apparent magnitude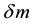 . An analytical expression for
. An analytical expression for  in terms of
in terms of 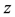 and n is derived. In Section 5, there is a description of how the curves for the distance modulus
and n is derived. In Section 5, there is a description of how the curves for the distance modulus 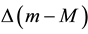 given in Tonry et al. [10] are used to obtain
given in Tonry et al. [10] are used to obtain 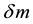 for the comparison between the accelerating universe for which one has
for the comparison between the accelerating universe for which one has