Received 10 August 2014; revised 5 September 2014; accepted 1 October 2014

ABSTRACT

A new updated simple local optical potential is proposed for analyzing low-energy π⁻-¹²C elastic scattering data at 80 MeV and below. This potential is composed of two real terms and an imaginary term. The nature of the real part of the potential is repulsive at smaller radii and attractive at larger ones. In fact, the height of the repulsive term is found to change linearly with the incident pion kinetic energy. On the other hand, the imaginary part of the potential is attractive, shallow and non-monotonic with a dip at about 1.6 fm. Such a nature of the potential makes it feasible to predict π⁻-¹²C cross sections at other energies in the energy region considered herein. Coulomb effects are incorporated by following Stricker’s prescription. This study will serve positively in studying both pionic atoms and the role of negative pions in radiotherapy.

Keywords:

Pion-Nucleus Potential, Elastic Scattering, Inverse Scattering Theory, Low-Energy Physics

1. Introduction

Pions play a major role in studying the nucleus and, as such, they are crucial in nuclear physics and other disciplines [1] [2] . For this reason, many pion facilities have been constructed to provide pions with both charges and different energies [3] . In the delta resonance region (T_π = 200 ± 100 MeV), the pion has a very small mean free path of less than 1 fm and usually faces a complete absorption at the surface of the nucleus. Such a scattering process of pions from different nuclei is usually described by simple optical potentials [4] . These potentials are usually reevaluated, and other theoretical models are also used to allow for achieving better results [5] . Even though, these potentials are criticized for several drawbacks mainly, not being able to account for large angle data [6] .

Recently Shehadeh et al. [7] have proposed a new simple local optical potential which proves to be successful in explaining the angular distributions of elastically scattered charged pions from different nuclei over the whole angular range in the delta resonance region. This potential relies on extracting potential points from available phase shifts using inverse scattering theory (IST), as a guide, and the full Klein-Gordon (K-G) equation with all necessary relativistic kinematical effects. Such a preferable success forms an inducement to extend the use of this potential in explaining the low-energy pion-nucleus data.

In the low energy region (T_π < 100 MeV), the pion has a large mean free path of few Fermi which enables it to penetrate deeply in the nucleus. As such, it can be used as a probe for studying the nuclear structure and discovering subtler aspects [8] of the pion-nucleus interaction. The accumulation of large amount of reliable low-energy pion-nucleus elastic scattering data compels theoreticians to build theories and formulate theoretical models in order to explain these data. Although the suggested theoretical potentials showed a reasonable success, but indeed it is not complete. In fact, these potentials have been criticized as difficult, impossible to interpret in physical terms, and didn’t provide a completely adequate description of the elastic scattering process [9] [10] . In view of this we’ll address here the use of our new potential, and testing the extent of its success, in analyzing low-energy π⁻-¹²C elastic scattering data.

In Section 2, the theory is presented. Section 3 is mainly concerned with results and discussion. The last section draws the conclusions.

2. Theory

The analytical form of our potential, usually used, has the following form:

(1)

Which consists of Satchler’s potential form [6] supplemented by the second term in Equation (1). In this study, and for the scattering of low-energy negative pions from a light nucleus (¹²C-nucleus), one may disregard the W₂ term, i.e. W₂ = 0, in Equation (1). As such, Equation (1) becomes

(2)

The parameters in this potential form are determined by implementing the IST outlined in Ref. [11] and will not be repeated here. Then a minimal number of parameters are adjusted to give a general nice fit to the measured cross sections, without losing the good match between the obtained potential points, real and imaginary, using IST from available phase shifts and the analytical forms, real and imaginary, of the potential, respectively. For charged pions, this can theoretically be tested by inserting this spherical symmetric potential in the radial part of K-G equation:

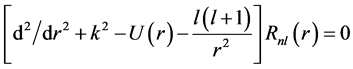(3)

In Equation (3), 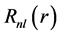is the r times the radial part of the wave function, also k² and 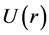are given by

(4)

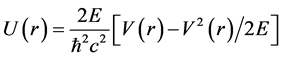(5)

where E, m, c, and 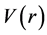are the effective pion energy, effective pion mass, velocity of electro-magnetic wave in vacuum and the complex pion-nucleus potential, respectively. Following Stricker’s prescription [12] , the Coulomb potential V_c is implicitly considered as a constant in. For π⁻-¹²C, V_c is taken +3.4 MeV for an effective Coulomb radius R_c = 2.54 fm.

To sustain the possibility of using available standard optical codes, Zemlyanaya et al. [13] have recently summarized the basic equations needed in transforming the true pion mass m_π and the pion bombarding energy in the laboratory system to the effective mass of the incident pion M_π and the actual beam energy 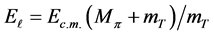where m_T is the target mass. The calculated values using Zemlyanaya et al.’s method agree very well with the values obtained from Satchler’s treatment. Zemlyanaya et al.’s method can be considered as another version of Satchler’s treatment. Here we adopt Zemlyanaya et al.’s method, and computer codes are modified accordingly. As such, one can start by calculating the pion’s momentum in the laboratory system 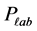using the equivalent form of the well-known relativistic energy-momentum relation:

(6)

and obtain

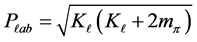(7)

The relativistic momentum of the pion in center-of-mass system P_cm can then be calculated,

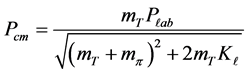(8)

So the total energy of the pion in the center-of-mass system E is given by

(9)

Comparing with Satchler’s treatment, E is M_π.

Since, one can find γ_π, and then the relativistic wave number of the pion k in the center-of-mass system,

(10)

where the constant (0.707447967) is not more than the ratio between the true rest mass of the pion m_πc² = 139.6 MeV and = 197.329 MeV∙fm.

One can now easily calculate the pion’s kinetic energy in the center-of-mass system (E_c.m.),

(11)

where the constant (20.90104704) is; and is the reduced mass of the two interacting particles in atomic mass units (u). In atomic mass units, the mass of the target nucleus m_T = 12u for ¹²C and.

3. Results and Discussion

The drawbacks of several theoretical models, as Kisslinger first-order pion-nuclear optical potential, to give a full understanding of π^±-nucleus elastic scattering data obliges theoreticians to solve this problem. As an example, Gmitro et al. [14] have supplemented the first-order pion-nuclear potential by a phenomenological ρ²-de- pendent term to give a reasonable explanation for the data. This was actually hinted by Johnson et al. [15] and embedded in the work of others [16] . Although Gmitro et al.’s full potential showed an improvement in analyzing the data, but it is still incomplete. In this work, we’ll continue using IST, as a guide, to obtain a potential which gives a remarkable consistent description of pion-nucleus interaction from 0 to 80 MeV.

The IST, used in extracting potential points from available phase shifts, has proved to be successful in determining the analytical form of the potential and its parameters. Such a potential has shown a remarkable success in describing nicely the elastic scattering of charged pions from calcium, calcium isotopes, ⁵⁴Fe [17] [18] and ¹²C above 100 MeV [19] , and from ⁴⁰Ca below 100 MeV [20] . Here, the same strategy has been used in determining the potential used for analyzing π⁻-¹²C elastic scattering data at several energies; namely at 80 MeV and below. Fortunately, and benefiting from the general trend and behavior of the extracted potential points from available phase shifts, the imaginary and real parameters of the potential are kept unchanged in the two energy sub-regions, 50 ≤ T_π < 100 and T_π < 50, except for the strength of the repulsive real part V₁ which is found to change linearly with the incident pion kinetic energy T_π. The potential parameters in Equation (2) are: V₀ = 37.0 MeV, R₀ = 3.75 fm, a₀ = 0.324 fm, R₁ = 3.00 fm, a₁ = 0.333 fm, W₃ = 100.0 MeV, R₃ = 1.70 fm, a₃ = 0.370 fm for T_π = 80, 69.5, 50 MeV. For T_π = 40, 30, 20 MeV, all these parameters are kept unchanged except R₀ = 3.95 fm and W₃ = 70.0 MeV. The parameter V₁ is found to change with T_π as V₁ = 18, 35, 70, 90, 110, 140 MeV for T_π = 80, 69.5, 50, 40, 30, 20 MeV, respectively. These values were fitted to a linear equation form, as shown in Figure 13, and the following relation is obtained:

(12)

The theoretical predictions of the differential cross sections deduced using our new complex potential defined in Equation (2) are compared with the experimental ones in Figure 2, Figure 4, Figure 6, Figure 8, Figure 10 and Figure 12 at 80, 69.5, 50, 40, 30 and 20, respectively. The potentials used in obtaining the theoretical differential cross sections are plotted in Figure 1, Figure 3, Figure 5, Figure 7, Figure 9 and Figure 11. The analytical forms of these potentials, with their real and imaginary parts, are compared with the potential points obtained from available shifts using IST at 80, 50, 40, and 30 MeV. Nevertheless, the calculated reaction cross sections are 332, 321, 181, 157, 152, and 138 mb at 80, 69.5, 50, 40, 30 and 20 MeV, respectively. They are in good agreements with the experimental ones [21] [22] .

The nature of the imaginary part of the potential is the same at all energies. It is non-monotonic and shallow with a minimum at about 1.6 fm. On the other hand, the real part is non-monotonic, shallow with a small repulsive core at 80 MeV which grows linearly as the pion’s incident kinetic energy decreases. In fact, it is repulsive at small radii (r ≤ 2.5 fm) and attractive at large ones (r > 2.5 fm). On the other hand, Figure 2, Figure 4, Figure 6, Figure 8 and Figure 10 show clearly that the calculated cross sections describe the data reasonably well. A similar nature for the potential, real and imaginary parts, was reported by Friedman [28] . For the 80 and 50 MeV cases, a reasonable number of phase shifts are available [23] , and deduced potential points from available phase shifts using IST are compared with the analytical forms of the potentials in Figure 1 and Figure 5. On the other hand, a small number of phase shifts available at 40 and 30 MeV [10] [23] were legitimately used to extract potential points using IST for a light nucleus (¹²C-nucleus) case with a radius of 2.54 fm. The extracted potential points are also compared with the analytical potential forms in Figure 7 and Figure 9. Nevertheless, and as Figure 8 and Figure 10 show, the agreement between calculated and measured angular distributions is excellent. In essence, it is very impressive to see the same potentials in each energy sub-region, except for V₁ parameter approximated from Equation (12), are very successful in accounting nicely for the data at all six energies: 80, 69.5, 50, 40, 30, and 20 MeV. Such a nature of the potential makes it feasible to predict the differential cross sections at other energies in a certain energy sub-region. As an example Figure 14 shows the predicted differential cross sections for the 60 MeV case, and the reaction cross section is 301 mb. It is also worthy to mention

that successful analyses of data at several energies reduces the ambiguity and selects a unique potential. The use of this successful potential can be tested at energies below 20 MeV for explaining pionic atom data, and a reasonable link may be established between pionic atom results and the scattering data. In contrast, Friedman et al. [29] have used optical potentials known from fits to pionic atom data to explain the observed cross sections.

As an important application for this investigation, Raju [30] has confirmed that negative pions, with energies considered herein, are of considerable interest and importance in radiotherapy. Low-energy negative pions can be captured by main tissue elements and provide kinetic energy enough to damage hypoxic cells in these tissue elements with no harm to other nearby cells.

4. Conclusion

The new updated potential proves to be successful in explaining low energy π⁻-¹²C elastic scattering data. In fact, the calculated differential and reaction cross sections are in nice agreements with the measured ones. It is interesting to see that the imaginary part of the potential, in each energy sub-region, is energy independent; and only the strength of the repulsive part V₁ of the real part decreases linearly as the incident pion kinetic energy T_π increases. This, and for the first time, establishes a relation between V₁ and T_π given by Equation (12). It is worth noting that when T_π ≈ 0, V₁ ≈ 172 MeV; and when T_π > 87 MeV, V₁ becomes negative. The nature of the potential makes it possible to predict the differential and reaction cross sections at other energy in the energy range of 20 - 80 MeV. Moreover, this investigation emphasizes the strength of IST in predicting our new updated potential which proves to be very successful in explaining low-energy π⁻-nucleus elastic scattering data. In addition, it will serve positively in both pionic atom studies and radiotherapy applications.

Acknowledgements

The author is very pleased to acknowledge the encouragement and financial support of the Deanship of Scientific Research at Taif University for carrying out this investigation. Many thanks go to Prof. F. B. Malik, to whom this paper is dedicated, for fruitful discussions.

References