Journal of Modern Physics
Vol.5 No.12(2014), Article
ID:48121,15
pages
DOI:10.4236/jmp.2014.512115
Transition Temperatures
Shpend Mushkolaj
Claragraben 116, Basel, Switzerland
Email: sh.mushkolaj@hispeed.ch
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 7 May 2014; revised 1 June 2014; accepted 21 June 2014
ABSTRACT
Despite intense experimental and theoretical efforts, it is still unclear why at temperatures of phase transitions, materials change completely their physical properties. Experimentally we are able to measure any microscopic, mesoscopic, and macroscopic variations of physical observables, but we still do not have a universal theoretical model that can predict all phase transitions, qualitatively and quantitatively. For instance, experimentally we can measure all physical properties of superconductors, but we do not have a unique theoretical model that is able to describe both types of superconductivity, namely the conventional and unconventional superconductivity. Here I present a simple quantum-mechanical and universal theoretical model that is able to calculate and predict critical temperatures for phase transitions: between magnetic order and disorder, superconductivity and normal conductivity, superconductivity and insulator, metal and insulator, melting and crystallization and many other phase transitions. All these phase transitions are described with four wave functions that are eigenfunctions of the Hamiltonian and the momentum operators.
Keywords:Transition Temperatures, Phase Transitions, Superconductivity, Magnetic Order, Hidden Order

1. Introduction
There is a widely held hypothesis which postulates that transition temperatures (Tc) need to be proportional to the order parameter p. For instance, magnetic order or spontaneous electric polarization needs to be proportional to their effective ordered magnetic and electric moments, i.e. Tc µ p2. However, experimental results negate very often this hypothesis, e.g., the Curie temperature of the order of 1000 K in ferromagnetic hexaboride compounds cannot be proportional to the effective magnetic moments, because in these compounds the ordered magnetic moments are very small, namely between 10−2 and 10−4 μB per formula. Although it is known that Iron impurities on the surface cause magnetic order, the intrinsic origin of the magnetic order is confirmed from many experimental results. There are other cases where the order parameter is unknown (hidden), e.g., the enigmatic phase transition at 17.5 K in URu2Si2. These phase transitions even after decades of intensive experimental research, remain enigmatic and confusing.
Why is it so important to understand the Tc-s? We have dreamt since decades to produce superconductors with transition temperatures at room temperature or higher, or why not produce organic superconductors. The current world energetic problem would be highly solved if we are able to produce room temperature superconductors. We will have a clue how to produce such materials only when we have a simple universal theoretical model that contains explicitly experimentally measurable observables, and we know exactly the dependency of the Tc functions from chemical composition and crystalline structure. Multiferroic materials are also very promising materials for future spintronic applications, and adjusting of the critical temperatures of these materials are of crucial importance.
We have many theoretical models that are able to explain the thermodynamics and predict many physical properties that change during phase transitions, e.g., the temperature dependence of specific heat, electric resistivity, magnetic susceptibility etc. Band theory calculations are able to predict many marvellous physical properties for solid state materials. In systems with a finite number of atoms molecular orbital models are able to predict exactly any energy excitation. Nevertheless, in spite of our giant achievements there are still many problems that we are not able to solve. One that I mention over and over is for instance our inability to predict transition temperatures for the phase transitions from unpolarized state to the spontaneous electric polarization and vice versa, that are shown in Table1
Why are we not able to predict transition temperatures? There might be several problems, but let me mention three of them: 1) electrical neutrality would simplify our models, but although it is everywhere in the microscopic and macroscopic worlds we do not find it in our models; 2) it is believed that atom-atom collisions in solid materials do not happen, and therefore the role of the atomic masses in phase transitions is highly neglected; 3) the fact that the elastic collisions are the only way to transport energy quanta in space and time from 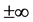 to
to ![]() is often not taken into account.
is often not taken into account.
Do we need a simple universal model that is able to predict transition temperatures or any energy gap (kBTc), and what are the main impulses that pushed me to search for such a model? Yes (some will disagree), as long as the simple universal model is based on the universal conservation laws of energy and momentum, is quantummechanical, there is no experimentally immeasurable (free) parameter, and is utilised as a “cooking recipe” to produce materials with required physical properties.
The three main impulses that pushed me to search for a simple universal model are as follows:
1) I worked in low temperature physics and every time when we switched on and off our superconducting magnets with the help of a resistive heater (persistent switch) that is in thermal contact with a segment of the superconducting wire I was fascinated, because the kinetic energy (this is proportional to the magnetic field strength) that we inserted with an external current source remained in the superconducting magnet conserved. This experimental fact ensured me that the conservation of the kinetic energy should be the kernel of the new model.
2) The second impulse came from the fact that I have studied the so called high Tc weak ferromagnets. These are Hexaboride compounds (such as CaB6, SrB6, BaB6) with no d-electrons but with very high Curie temperatures. These materials have effective ordered magnetic moments of the order between 10−2 and 10−4 μB per formula unit and a Tc of ~1000 K. This is totally in disagreement with the Curie temperature formula that is proportional to the effective number of the ordered magnetic moments1. From ferromagnetic Hexaborides I understood
Table 1 . Different compounds, type of electric order, experimental Curie temperatures and fitted (calculated) Tc-s. These data were obtained from Ref. [1] .
that we need a completely new model that can explain the high Tc weak ferromagnetism, and is independent on the ordered magnetic moment.
3) Iron is the simplest ferromagnetic solid with a cubic crystalline structure. The distances between ordered magnetic moments are equal to the lattice constant of 2.866 Å, i.e., the same thing (parallel oriented magnetic moments) is repeated in the real space and in time. This space and time periodicity can be described quantummechanically with plane wave functions. Since any unit cell is electrically neutral, I need only kinetic parts of the atomic and electron Hamiltonians.
From the superconducting magnets I felt that kinetic energy (Ekin) should be conserved in the collective quantum states, but the problem was, how can Ekin propagates to the ±∞. Elastic collisions are the only way, but if we think classically (central elastic collisions between a heavy atom and the light electron) electrons should vibrate only between two heavy atoms (i.e., the Ekin is located between two atoms). The solution was to create an electrically neutral particle from the kinetic energy and momentum conservation laws that allows the propagation of the Ekin to ±∞ distances and to perpetuity. I found that such particles should have masses of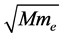 , were M and me represent the masses of atoms and electrons, respectively. My prime calculation was the Curie temperature of Iron with an experimental value of 1043 K. In my Tc formula I inserted the atomic mass of Iron, free electron mass, and the lattice constant of 2.866 Å, and I got the value of 1043 K.
, were M and me represent the masses of atoms and electrons, respectively. My prime calculation was the Curie temperature of Iron with an experimental value of 1043 K. In my Tc formula I inserted the atomic mass of Iron, free electron mass, and the lattice constant of 2.866 Å, and I got the value of 1043 K.
In this paper at first I will derive the Tc functions for elastic collisions from the plane wave eigenfunctions of the Schrödinger Equation. In the Section 3 I explain how kinetic energy can be arrested through elastic springs into the solid. From the elastic springs I derive Tc functions that are just the inverse of the Tc functions derived from the elastic collisions. Section 3 is separated into three main subsections, namely, magnetic order, superconductivity, and hidden order. Section 4 summarizes the calculations obtained for each type of phase transitions and presents some conclusions.
2. Derivation of the Tc Functions
Let us start from the fact that matter is electrically neutral, i.e., and the total number of positive protons and negative electrons are equal. Electrical neutrality scales from neutrinos, neutrons, atoms, molecules, crystalline unit cells, etc., to the macroscopic objects such as planets and stars. Here, I consider only ordered solids, i.e., three-dimensional crystals that are networked from one-dimensional atomic chains. In some of these one-dimensional atomic chains the elastic atom-atom, electron-electron and atom-electron collisions may appear, which are the origin of phase transitions.
In spite of electrical neutrality, we know that inside the unit cells reside electrically charged ions and electrons that interact electromagnetically with each other. But let us analyse first, what is the role of the electromagnetic interactions in crystals. At the absolute zero atoms do not vibrate, i.e., they rest on their equilibrium positions and there are no fluctuations of magnetic and electric moments and the total energy of systems are solely of electrostatic and magnetic origin. Therefore, the role of the electromagnetic interactions is the control of the equilibrium positions of ions and of the fixed orientations of magnetic and electric dipole moments, to reword it is responsible for the periodicity in real space. When we heat the system above the absolute zero, atoms vibrate around their zero-Kelvin positions and magnetic and electric moments fluctuate around their polarization directions. Vibration and fluctuation amplitudes increase with increasing temperature, and at a critical temperature, moments become disoriented or the distances between atoms in 1D atomic chain may vary strongly (e.g., melting of a solid crystal). In general at the critical temperatures systems switch over from disordered (T > Tc) to the ordered (T < Tc) collective quantum states, i.e., the potential energy (electromagnetic interactions) at T = Tc is equal to the kinetic energy. Therefore, we claim that the critical temperature unless it is the measure of the kinetic energy, it yields also information on the strength of the potential energy at T = 0 K that is responsible for the static spatial order of ions, polarization of magnetic and electric moments, superconductivity and other collective quantum states.
Let us analyse for example the superconducting magnets at the absolute zero temperature. If the charge carriers (electrons or holes) are frozen at T = 0 K, the magnetic field should be zero, if we insert kinetic energy with an external current source, magnetic field becomes nonzero and it remains constant in time. There is an upper limit (critical current and critical magnetic field) of the kinetic energy that can be inserted into the superconducting magnet. The nonzero magnetic fields in permanent magnets and superconducting magnets indicate that charge carriers rotate with a kinetic energy even at T = 0 K.
What about the atoms, do they vibrate (collide) at zero Kelvin? The isotope effect ensures us that atoms (ions) cooperate with charge carriers even at the absolute zero, i.e., their kinetic energies are nonzero and conserved. For two vibrating neighbour atoms the term collision may be more appropriate. This is justified by the fact that atom radii are smaller or equal to the half atom-atom distances, and very small vibrations cause the kinetic energy propagation through the electrostatic repulsions between electron clouds. These atomic vibrations are equivalent to the neutral atom-atom, cation-cation, anion-anion and atom-ion collisions (in following all these types of collisions I will call as atom-atom collisions). It is obvious that cation-anion collisions cannot be elastic because of their attractive electrostatic interaction.
Because solids are very dense and electrons move permanently, it is impossible to exclude the possibility that electrons and atoms collide with each other, these collisions at the phase transitions needs to be elastic, otherwise, the kinetic energy will dissipate with time.
To arrest the kinetic energy into solid materials it is not enough just to have elastic collisions in bulk. What happen when the next-to-last atom collides with outermost (last) atom? For the outermost atoms in the atomic chains we need elastic springs since they have only one neighbour atom. These elastic springs are needed to transform the kinetic energy into potential energy (U) and vice versa (see Figure 1). No kinetic energy is dissipated into heat if and only if the condition U = Ekin is fulfilled. There are several cases where the influence of the outermost atoms is very strong, e.g., in the superconducting or magnetically ordered thin films. Application of the external pressure, especially in thin films, could tune also the force constants of these elastic springs until the Ekin is arrested into the system. If the springs of the outermost atoms are not elastic, the kinetic energy dissipates into heat and the periodicity in time and space decay slowly.
The plan wave functions are simplest and unique way to describe quantum mechanically the time and space (real space) periodicity of the kinetic energy and momentum propagation:
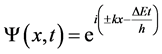 and
and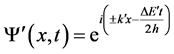 . (1)
. (1)
Is it reasonable to describe an ordered many particle system with just four plane wave functions? I think yes, let us analyse, e.g., the ferromagnetic state of iron, all what we have, are the parallel ordered magnetic moments located in distances of 2.866 Å. If the propagation of the kinetic energy starts at time zero we know that during propagation in 1D atomic chain we get always the same thing (parallel oriented magnetic moments) at distances 2.866 Å and at undetermined time periods of t. This space and time periodicity propagates from ±∞ distances to
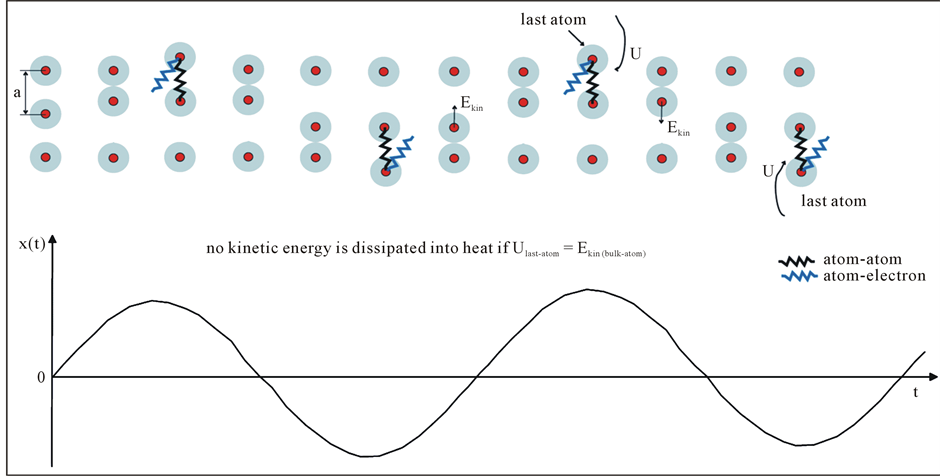
Figure 1. A schematic representation of the elastic atom-atom collisions, elastic atom-atom springs (black) and atom-electron springs (blue). Elastic atom-atom springs connect the outermost atoms with the next-to-last atoms, elastic electron-atom springs connect outermost atoms with electrons. The diagram below represents the time periodicity of the atomic displacements.
perpetuity, at any temperature between 0 K and 1043 K.
These plane wave functions are simultaneously eigenstates of the Hamiltonian operator of two elastically colliding particles with masses M1 and M2 and momentum operator (ħ/i)Ñ, i.e.,:
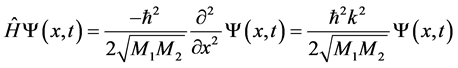 , (2a)
, (2a)
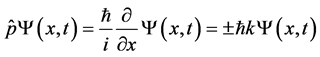 . (2b)
. (2b)
The propagation of the kinetic energy is given by the time-dependent Schrödinger wave equation:
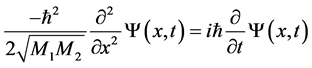 . (3)
. (3)
After inserting the plane wave functions from Equation (1) into the time-dependent Schrödinger Equation (3), we get:
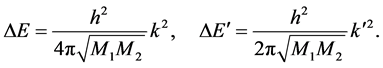 (4)
(4)
where, k and k' represents the wave numbers of the electrically neutral particles with masses 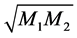 in the collision direction. Inserting k, k',
in the collision direction. Inserting k, k', 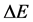 , and
, and ![]() from Equation (5) into Equation (4),
from Equation (5) into Equation (4),
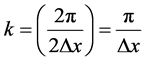 ,
, 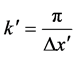 ,
, 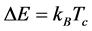 and
and 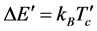 (5)
(5)
we get the following two formulas for transition temperatures:
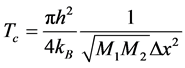 , (6a)
, (6a)
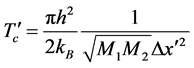 . (6b)
. (6b)
where, h and kB represent Planck constant and Boltzmann constant, respectively. In the case of elastic atomatom collisions 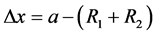 and
and  represent the covered distances between atoms (ions) at the moment of collisions (vibrations); a, a', and R1, R2 are the equilibrium distances between atoms and the atomic (ionic) radii, respectively. For elastic electron-atom and electron-electron collisions Dx and Dx' represent the magnitudes
represent the covered distances between atoms (ions) at the moment of collisions (vibrations); a, a', and R1, R2 are the equilibrium distances between atoms and the atomic (ionic) radii, respectively. For elastic electron-atom and electron-electron collisions Dx and Dx' represent the magnitudes  of direct lattice vectors. With the above universal formulas that differ from each other only by a factor of two, one can predict any critical temperature for any phase transition.
of direct lattice vectors. With the above universal formulas that differ from each other only by a factor of two, one can predict any critical temperature for any phase transition.
As mentioned above, three-dimensional crystals are networked from one-dimensional atomic, ionic, or molecular chains. Along these 1D chains move light charge carriers (electrons or holes), collide elastically with each other or with atoms, and vibrate (collide) the heavy atoms, ions or molecules. In general there might be three main types of elastic collisions, namely: atom-atom (or ion-ion), electron-electron, and electron-atom. The kinetic energy and momentum that propagates during these elastic collisions bear the corresponding masses: ,
, 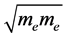 , and
, and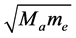 .
.
3. Applications of the Tc Functions and Introduction of Elastic Springs
3.1. Magnetic Order
Iron is the simplest ferromagnetic solid with a Curie temperature of 1043 K. The crystal structure is body-centred cubic with a lattice constant of 2.866 Å. For elastic atom-electron collisions M1 = MFe and M2 = me (me is free electron mass) and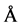
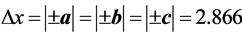 , from (6a) we get a Tc of 1043 K. From (6b) and
, from (6a) we get a Tc of 1043 K. From (6b) and  we get exactly the same result.
we get exactly the same result.
Let us analyse the elastic atom-atom collisions. Depending on the spin state iron atoms have different radii, namely: 1.32 Å for low spin and 1.52 Å for high spin iron [2] . Since the sum of two high spin radii is 3.04 Å, and this is larger than the lattice constant we can say, that their electron clouds are overlapped. In other hand the sum of two low spin radii is 2.64 Å, which is smaller than the lattice constant. In this case iron electron clouds are not overlapped and there is a short distance of Dx = a ‒ (R1 +R2) = 0.226 Å for vibration amplitude. From formula (6b) we get a value of 1046 K for Tc.
For elastic electron-electron collisions we get a
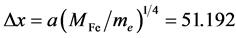 , but at the moment it will be very speculative to interpret this Dx. At the end of this section I will relate it to the elastic springs, sound velocity, and lattice constant.
, but at the moment it will be very speculative to interpret this Dx. At the end of this section I will relate it to the elastic springs, sound velocity, and lattice constant.
I claimed above that, to arrest the kinetic energy into solid materials in addition to the elastic collisions in the bulk, elastic springs are needed that transform the kinetic energy into the potential energy and vice versa (i.e. these elastic spring do not let the kinetic energy to escape from the crystal). These elastic springs connect the outermost atoms, electrons and quasiparticles (MFeme)1/2 with the bulk.
We derive the formula for spring constant from the group velocity [3] of the sound waves that is:
 . (7)
. (7)
where, f, M, k and a represents the spring constant, the mass of the vibrating particle, the wave-number, and the lattice constant, respectively. Since the wavelengths of the sound waves are much longer than lattice parameters, we have 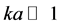 (i.e., cos(ka/2) = 1), and from the Equation (7) we get the following equations for spring constants:
(i.e., cos(ka/2) = 1), and from the Equation (7) we get the following equations for spring constants:
 ,
, 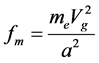 and
and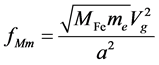 . (8)
. (8)
Below the Curie temperature collisions between particles are elastic for long times and long distances. Because of this fact, it is comprehensible to claim that the propagation of the sound waves is also adiabatic. The experimental values for the sound speed in iron are between 5120 m/s [4] and 4910 m/s [2] . For our spring constant calculations we take the average value of Vg = 5015 m/s and a = 2.866 Å. From Equation (8) we get: fM = 28.59 N/m, fMm = 8.89 ´ 10‒2 N/m, and fm = 2.78 ´ 10‒4 N/m. These elastic springs can store the corresponding potential energies:
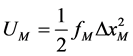 ,
, 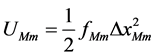 , and
, and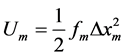 , (9)
, (9)
where, DxM, DxMm, and Dxm are the displacements during the elastic atom-atom, electron-atom and electronelectron collisions.
As I pointed out above, to arrest the kinetic energy into a crystal, the sum of the total potential energies stored in elastic springs needs to be equal to kBTc, i.e.,:
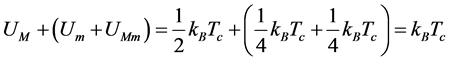 . (10)
. (10)
Hence follows that:
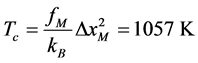 ,
,  , and
, and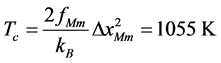 . (11)
. (11)
As one can see, the relation of the elastic collisions to the elastic springs produced two inverse Tc-functions of the forms:
 and
and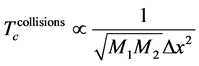 . (12)
. (12)
The three intersection points of these two functions appear at the temperature of 1043 K and three different distances (i.e., DxM, DxMm, and Dxm). These distances represent the distanced between colliding particles and the sprig stretch lengths in Hooke’s region. In the case of iron, there are total nine positive intersection points between these two types of Tc functions. A detailed discussion of these intersection points goes beyond the scope of this paper.
3.2. Superconductivity
Since elastic atom-atom collisions are the simplest way to relate the Tc to the crystalline structure and atomic radii, I use mainly this type of collisions to calculate superconducting Tc-s. High-Tc superconductors are more interesting because in these materials also the elastic electron-atom and electron-electron collisions can be easily related to the crystalline structure. In the following I will use the minus sign instead of the conventional overbar for specifying directions of lattice points in real space ±n1a ± n2b ± n3c from the origin, i.e., [±n1, ±n2, ±n3].
LaFePO is a superconductor with a onset transition temperature of 7.4 K [5] . The layered crystal structure of LaFePO is a tetragonal of ZrCuSiAS type with lattice parameters a = 3.9610(1) Å and c = 8.5158(2) Å. In the following I calculate the Tc (when I calculated the Tc of 7.4 K, I was disappointed, since at the time when I have done these calculations it was reported that the Tc for LaFePO is 7K) based on the elastic atom-atom collisions.
La chains: Along the [±1, ±1, 0] directions of the real space, for the maximal vibration amplitude of  with atomic radius RLa = 1.95 Å, we calculate a Tc of 7.4 K.
with atomic radius RLa = 1.95 Å, we calculate a Tc of 7.4 K.
Fe chains: Along the [±1, ±1, 0] directions of real space, at the maximal vibration amplitude of
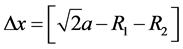 with atomic radius R1 = 1.40 Å and R2 = 1.52 Å, we get a Tc of 7.4 K. In the [±1, 0, 0]
with atomic radius R1 = 1.40 Å and R2 = 1.52 Å, we get a Tc of 7.4 K. In the [±1, 0, 0]
and [0, ±1, 0] directions, for 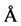
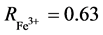 and
and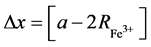 , we get a Tc of 7.3 K.
, we get a Tc of 7.3 K.
P chains: Along the [±1, ±1, 0] directions of real space, at the maximal vibration amplitude of 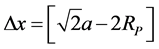 with atomic radius RP = 1.4 Å, we calculate a Tc of 7.4 K.
with atomic radius RP = 1.4 Å, we calculate a Tc of 7.4 K.
O chains: Along the [±1, ±1, 0] directions, there are elastic intramolecular O-O collisions, where the minimal distance between oxygen mass centres is equal to the empirical atomic radius of oxygen that is 0.6 Å. In this case, 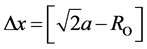 , and we get a Tc of 7.4 K. Along [0, 0, ±1] directions O−1-O−1 elastic collisions with
, and we get a Tc of 7.4 K. Along [0, 0, ±1] directions O−1-O−1 elastic collisions with
 , where
, where  = 1.76 Å, we calculate a Tc of 7.4 K.
= 1.76 Å, we calculate a Tc of 7.4 K.
There are many other solutions to calculate the Tc from elastic atom-atom collision, and atom-electron collisions, but rather we try to find an elastic spring that can arrest the kinetic energy of kBTc (with Tc = 7.4 K). From the bulk modulus of 96.2 GPa [6] and the mass density of ρ = 3933 kg/m3, we can estimate the sound velovity, that is:
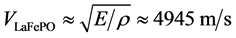 . (13)
. (13)
From Equation (8) I can estimate the spring constant between electrons, which is fm = 1.416 ´ 10‒4 N/m. Since the radius of electrons is negligible small we take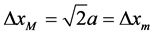 , and from the Equation (11) we get a Tc of 6.4 K, i.e., the Tc function of atom-atom collisions cut the Tc function of the electron-electron springs. This means electron springs are able to arrest the kinetic energy that propagate with elastic atom-atom collisions.
, and from the Equation (11) we get a Tc of 6.4 K, i.e., the Tc function of atom-atom collisions cut the Tc function of the electron-electron springs. This means electron springs are able to arrest the kinetic energy that propagate with elastic atom-atom collisions.
Superconductors of the group 13 are: aluminium, gallium, indium and thallium, with the superconducting Tc-s of: 1.175 K, 1.083 K, 3.4 K and 2.38 K, respectively. In some cases, the electronic configurations imply different equally possible combinations which do not allow propagation of kinetic energy of elastic “single-atom”- “single-atom” collisions. Therefore, we are forced to consider elastic collisions between clusters of atoms. If there are n different combinations we need clusters of (n + 1) atoms to get the energetic replications along the atomic chain. In the following I will try to explain these situations.
In the Figure 2 we present the clusters with 9-atoms that result from the ground state electronic configurations [inert element] ns2, np1 (n = 3, 4, 5, 6). As one can see we get 8 different equally probable combinations that result from the spin combinations ±px , ±px ¯, ±py , and ±py ¯ and from the electrostatic interactions. Since the kinetic energy is arrested into the superconductor energetic replications, the first and the last atom within a cluster needs to be at the same state. In the case of the group 13 elements we need clusters with (8 + 1)-atoms.
In the Table 2 are listed the obtained Tc values by considering the elastic collisions between 9-atom clusters for: Al, Ga, In and Tl.
The factor 9 can be found also in the elastic electron-atom collisions. By inserting the following masses and distances into the Equation (6a):
 ,
, 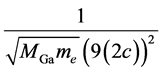 ,
, 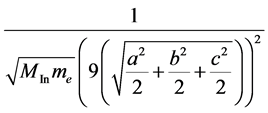 ,
, 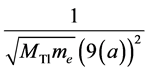 ,
,
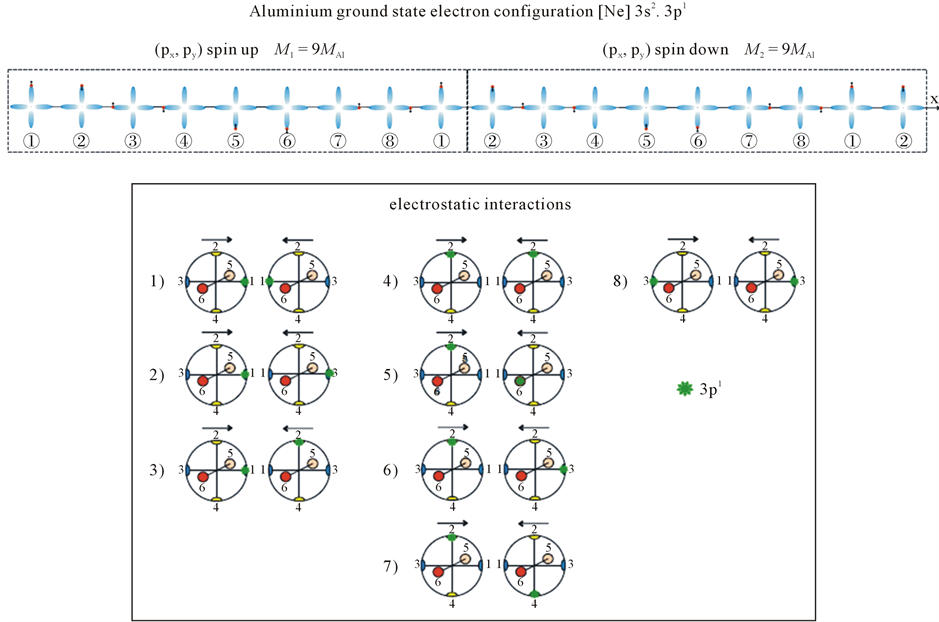
Figure 2. The valence electrons in np1 states yield the 9-atom clusters. The 8 different equally probable combinations, that results from the spin combinations ±px , ±px ¯, ±py , and ±py ¯, and from the electrostatic interactions.
Table 2. Calculated Tc-s for Al, Ga, In and Tl with corresponding lattice parameters: (a = b = c = 4.0495 Å), (a = 4.5192 Å, b = 7.6633 Å, c = 4.526 Å), (a = 3.2523 Å, b = 3.2523 Å, c = 4.9461 Å), and (a = b = 3.4566 Å, c = 5.5248 Å).
we get the corresponding Tc-s of: 1.16 K, 1.15 K, 3.23 K and 2 K, which are in agreement with the calculated values for elastic atom-atom collisions.
Which electronic configuration is the best suitable for superconductivity?
The spherical symmetry of the s-valence electrons destroy the collective quantum state of superconductivity, because between the minimal and maximal Coulomb interactions there is a very large number of different equally probable combinations. In the Figure 3 I show some different equally probable and non-degenerated combinations between the maximal and minimal Coulomb interactions. To get the repetition of the first state we need very large atomic clusters, and this leads to the superconducting Tc-s close or equal to zero Kelvin.
In multi-component compounds the first check that I usually do is, if there is oxygen in the formula unit, because I am sure that, oxygen usually contributes to any phase transition. This was one practical experience during my innumerable Tc calculations.
Elements with valence electrons in np4 (oxygen belongs to this group) are the most suitable elements for superconductivity, because during atom-atom collisions in 2D space there is only one possible combination (see Figure 4), and therefore we need singe atoms to collide with each other. In the oxidation state-2 there is also one possible combination yet in the 3D space.
In some cases the spherical s-orbital may be deformed through hybridisation, overlapping of s-electrons with non-spherical orbitals (p, d, f) or by compressing under high external pressures. Such deformed s-orbitals may become superconductive. One interesting example is the superconducting lithium.

Figure 3. Here we show some different equally probable and non-degenerated combinations during atom-atom collisions where valence electrons are in the spherical ns1 orbital.

Figure 4. Schematic representation of elastic O-O collisions.
Superconducting lithium: In the multi-component compound of LiFeAs, the spherical symmetry of the s electrons of Li may be abrogated through s-d and s-p overlapping with iron and arsenic valence orbital. Since electro-negativity differences between three elements are between 0.85 and 1.2 the bonds are polar covalent, and therefore s-d and s-p orbital overlapping are possible. We can test the existence of this overlapping by calculating the Tc of the elastic (LiFe)-(LiFe)-(LiFe) and (LiAs)-(LiAs)-(LiAs). In the Table 3 we show some of the elastic atom-atom collisions that contribute to the onset of superconductivity in LiFeAs.
As one can see, in fact the molecules (Li1+Fe) and (Li1+As1−) yield the exact experimental values for Tc, i.e., the spheres of s-orbital are deformed and therefore there is also a contribution of elastic Li1+-Li1+ collisions in the low-Tc directions, namely [0, 0, ±1]. Now we calculate the spring constants of the elastic springs that are able to arrest the kinetic energy inside the crystal. Let start with the Li1+-Li1+ collisions; these collisions I connect with the electron-lithium springs. Inserting the calculated bulk modulus of 93.4 GPa [7] and mass density of 5059 kg/m3 into Equation (13) we get a sound speed of 4296.7 m/s. The spring constant and the Tc for electron-Li springs in [0, 0, ±1] are given as:
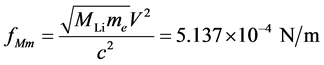 ,
, .
.
Applying high external pressures leads also to the deformation of the s-orbital and superconductivity appears between 5 K and 14 K [8] . In a next paper I will fit the Tc-s as function of the external pressure for superconducting lithium.
La2CuO4+y is classified in the group of unconventional superconductors and has three transition temperatures [9] : Tc1 » 16 K, 32 ≤ Tc2 ≤ 36 K, and 40 ≤ Tc3 ≤ 45 K. The crystalline structure is orthorhombic with lattice parameters [10] : a = 5.406 Å, b = 5.37 Å, and c = 13.15 Å. In the following I present some of the possible elastic atom-atom collisions that contribute to the onset of superconductivity.
O chains: Along the [±1, ±1, 0] directions of real space, the shortest O-O distance is . For empirical covalent radius of RO = 0.73 Å [2] , we imagine two types of O chains—the ∙∙∙-O-O-O-∙∙∙ and the ∙∙∙-2O-2O-2O-∙∙∙—with masses M1 = M2 = MO and M1 = M2 = 2MO respectively. The maximal vibration amplitude for these vibrations is given as:
. For empirical covalent radius of RO = 0.73 Å [2] , we imagine two types of O chains—the ∙∙∙-O-O-O-∙∙∙ and the ∙∙∙-2O-2O-2O-∙∙∙—with masses M1 = M2 = MO and M1 = M2 = 2MO respectively. The maximal vibration amplitude for these vibrations is given as: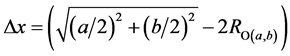 . We get two Tc values that agree with the experimental results for Tc1, and Tc2: 16.8 K and 33.77 K for 2O-2O and O-O collisions, respectively.
. We get two Tc values that agree with the experimental results for Tc1, and Tc2: 16.8 K and 33.77 K for 2O-2O and O-O collisions, respectively.
Cu chains: The shortest Cu-Cu distance in [±1, ±1, 0] direction is also equal to: . Similarly to O chains, we imagine two types of copper “atomic Newton cradles”: one ∙∙∙-Cu-Cu-Cu-∙∙∙ and the other ∙∙∙-2Cu-2Cu-2Cu-∙∙∙ with masses M1 = M2 = MCu and M1 = M2 = 2MCu respectively. The maximal vibration amplitude for copper vibrations is given as:
. Similarly to O chains, we imagine two types of copper “atomic Newton cradles”: one ∙∙∙-Cu-Cu-Cu-∙∙∙ and the other ∙∙∙-2Cu-2Cu-2Cu-∙∙∙ with masses M1 = M2 = MCu and M1 = M2 = 2MCu respectively. The maximal vibration amplitude for copper vibrations is given as: . The calculated Tc-s for different types of Cu radii are listed in Table4 Vibrations of ∙∙∙-2Cu-2Cu-2Cu-∙∙∙ chain give a Tc of 17 K that agrees with the experimental value of Tc1.
. The calculated Tc-s for different types of Cu radii are listed in Table4 Vibrations of ∙∙∙-2Cu-2Cu-2Cu-∙∙∙ chain give a Tc of 17 K that agrees with the experimental value of Tc1.
Cu-O chains: For collisions in aand b-directions, the ∙∙∙-Cu-O-Cu-O-Cu-O-∙∙∙ chains may contribute to the onset of superconductivity. In a-direction, the Cu-O pairs vibrate with amplitudes of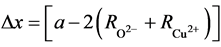
Table 3. Calculated transition temperature for tetragonal LiFeAs with lattice parameters: a = b = 3.791 Å and c = 6.364 Å. The experimental value for Tc is ~18 K.
Table 4. Calculated transition temperatures for ∙∙∙-Cu-Cu-Cu-∙∙∙ chain and different types of atomic radii. The atomic radii were obtained from Ref. [2] .
and M1 = MO and M2 = MCu. For 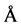
 and
and
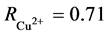 , we get a Tc of 41.3 K. In b-direction with
, we get a Tc of 41.3 K. In b-direction with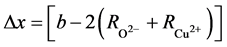 , we get 43.3 K for Tc.
, we get 43.3 K for Tc.
La chains: In [±1, ±1, 0] directions, the ∙∙∙-La1-La2-La1-La2-∙∙∙ chains may contribute to the onset of superconductivity at 40.3 K for M1 = M2 = MLa, RLa1 = 1.69 Å, RLa2 = 1.39 Å and
 .
.
La-O chains: In [±1, ±1, 0] directions, the ∙∙∙-La-O-La-O-La-O-∙∙∙ chains may contribute to the onset of superconductivity at 44 K for M1 = MLa, M2 = MO, RLa = 1.95 Å, RO = 0.66 Å and
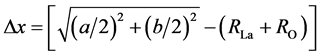 .
.
Elastic electron-O, electron-Cu and electron-La collisions induce also the onset of the superconductivity in this compound. In the Table 5 are listed the obtained Tc values by considering the elastic electron-atom collisions.
One may find more elastic electron-atom collisions that induce superconductivity, but at the moment, my aim was just to prove that additionally to the elastic atom-atom collisions also the elastic electron-atoms collisions contribute to the superconductivity.
What about the elastic electron-electron (e-e) collisions, do they contribute to the superconductivity?
Yes. This one may proof from the critical carrier concentration. It is known that the insulating parent compound La2CuO4 becomes superconductive by doping beyond a critical carrier concentration of 0.0605 [11] . This means that to induce the insulator-superconducting transition we need at least 0.0605 electrons per unit cell.
How many diagonal lengths  are needed to get one electron with the mass equal to the mass of the free electron?
are needed to get one electron with the mass equal to the mass of the free electron?
One very simple answer would be, exactly 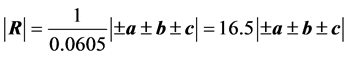 diagonals are needed to get one electron with a mass that is equal to the free electron mass. If these two electrons collide elastically with each other than we obtain a Tc value that is exactly equal to the experimental value (see Table 6). A second answer may say, in the directions [±1, 0, 0] and [0, ±1, 0] collide elastically two Cooper pairs, i.e., 2e-2e collisions. We get again one superb agreement with experiment. A third answer would be, electrons collide elastically with the over-next electrons in [±1, ±1, 0] directions.
diagonals are needed to get one electron with a mass that is equal to the free electron mass. If these two electrons collide elastically with each other than we obtain a Tc value that is exactly equal to the experimental value (see Table 6). A second answer may say, in the directions [±1, 0, 0] and [0, ±1, 0] collide elastically two Cooper pairs, i.e., 2e-2e collisions. We get again one superb agreement with experiment. A third answer would be, electrons collide elastically with the over-next electrons in [±1, ±1, 0] directions.
Let us find at least an intersection point between the two types of Tc functions. From bulk modulus of 185 GPa [12] and mass density of 7107 kg/m3 we can estimate the sound velocity of ~5100 m/s. One of the possible spring constants and the Tc-s for electron-electron springs in [±1, 0, 0] are given as:
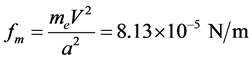 ,
,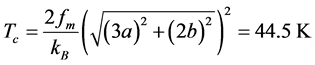 .
.
Table 5. Calculated transition temperatures for orthorhombic La2CuO4 from elastic electron-atom collisions.
Table 6. Calculated transition temperature from elastic e-e collisions.
3.3. Hidden Order
The semimetal URu2Si2 exhibits an enigmatic transition at Tc = 17.5 K to a hidden collective quantum state for which the order parameter remains unknown after 25 years of intense experimental and theoretical research. Beside innumerable experiments there are circa 25 theoretical models that try to explain this enigmatic transition. Here I will try to explain this enigmatic phase transition based on the elastic atom-atom, atom-electron and electron-electron collisions, and find the elastic spring that could arrest the kinetic energy inside the crystal.
In comparison with the superconductivity where many elastic atom-atom collisions may be found, in URu2Si2 seems that the number of solutions based on elastic atom-atom collisions is much smaller, namely I found at least one solution, that is given as:
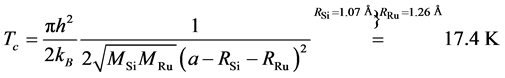 .
.
One can find many different solutions from elastic electron-atom collisions, some of them are listed in the Table7
The long range antiferromagnetic order may be caused by the elastic e-Ru collisions in the c direction. Experimental results reveal an ordered magnetic moment of 0.03 µB/fu in the c-direction. In the isostructural DyRu2Si2 the Ru magnetic moment was calculated to be of the order of 0.02 µB/fu [13] . Therefore one may speculate that elastic e-Ru collisions cause the antiferromagnetic order along c-direction. However, the small magnitude of the ordered magnetic moment is inconsistent with the large value of the entropy associated with the specific heat anomaly at 17.5 K. How can we explain this inconsistency? From the Table 7 one can see that in addition to the antiferromagnetic electron-Ru collisions in c-direction, there are many other hidden elastic electron-Si, heavy electron-U, electron-(RuSi)1/2 and another electron-Ru in [±4, 0, ±1] direction collisions, which cannot be experimentally proven (i.e., the above mentioned elastic collisions do not cause magnetic order, crystalline structure change, spontaneous electric polarisation, superconductivity and any measurable transformations). During the cooling of the sample at 17.5 K lot of heat needs to be released (exothermic) because of occurrence of these many quantum states (elastic collisions) and a large entropy reduction is expected. During the heating from a T <17.5 K to 17.5 K, lot of heat needs to be absorbed (endothermic) into the system and a large entropy increase is expected.
Below 17.5 K the Hall effect measurements reveal a carrier concentration of the order of n = 6 ´ 1020 cm‒3 [14] , this is equal to 0.0488 carriers per formula unit. Since the antiferomagnetic order is in the c-direction and the same state repeats (spin up or spin down) at the distances of 2c, for 0.0488 carriers per formula unit the space periodicity in c-direction would be equal to 2c ´ 0.0488‒1 Å. For elastic charge carrier-charge carrier collisions with masses equal to the free electron mass and in the c-direction we get a Tc that is:
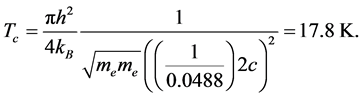
Which are the elastic springs that are able to arrest the kinetic energy into the crystal? From the experimental results in the high quality URu2Si2 single crystal, it was found that a minimum in C11 (T) modulus appears at 20
Table 7 . Calculated Tc-s from Equation (6b) for elastic collisions of electrons and heavy electrons with Ru, Si, (RuSi)1/2 and U in different crystalline directions.
K, this temperature is very close to the Tc of 17.5 K and a step-like anomaly at the superconducting Tc [15] . Let us calculate the kinetic energy that the spring constant C11 can arrest in the compound URu2Si2. For C11 (20 K) = 255 GPa and the mass density of ρ = 10009 kg/m3 we get a sound speed of Vs = 5047 m/s. Independently on the crystalline direction the electron-electron springs are able to arrest a kinetic energy that is given as:
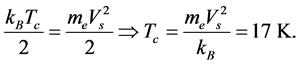
4. Summary and Conclusions
In this paper I presented the model of the elastic atom-atom, atom-electron and electron-electron collisions described by four plane wave functions. Transition temperature functions are derived from the solutions of the time dependent Schrödinger equations. I calculated the transition temperatures of ferromagnetic Fe; superconductors: of LaFePO, Al, Ga, In, Tl, LiFeAs, and La2CuO4; and hidden order in URu2Si2. To arrest the kinetic energy that propagates through elastic collisions I have assumed the existence of elastic springs for the outermost particles. Combining elastic springs with elastic collisions produced two inverse Tc functions. The intersection points of these two inverse Tc-functions, may be related to the kinetic energy conservation at temperatures ≤Tc. I have explained which electronic configuration is more suitable for superconductivity, and why spherical s-orbitals are not adequate for high Tc superconductivity. The role of the sound velocity in building the collective quantum states has been shown. Since sound velocity depends directly from the mechanical and elastic properties of the solid materials, we can analyse and predict the transition temperatures in relation to these properties, crystalline structure, chemical composition and electronic configurations of each atom. To arrest the kinetic energy during the superconducting phase transition, electron-electron springs are introduced beside atom-atom and (electron-atom)-(electron-atom) springs. These electron-electron springs are the best equivalent to the attractive interaction between electrons which is the basic assumption of BCS theory.
Here I have passed on the Tc predictions, because in this paper, my aim was just to show the universality of the model and to explain how the kinetic energy can be arrested into the solid materials. In a next paper I will take a chance to do Tc predictions, and to explain many other physical phenomena, such as isotope and Meissner effects, London penetration depths, critical magnetic field and pressure and doping dependences of the Tc functions.
Acknowledgements
I would like to thank Prof. Roald Hoffmann for his constructive critics and motivating me to keep trying on getting my work published, and Prof. Pekka Pyykkö for enlightening discussions on atomic radii.
References
- Strukov, B.A. and Levanyuk, A.P. (1997) Ferroelectric Phenomena in Crystals. Springer, Madrid.
- www.webelements.com
- Kittel, C. (1971) Introduction to Solid State Physics. 4th Edition, Wiley, New York.
- www.wikipedia.org
- Yamashita, M., Nakata, N., Senshu, Y., et al. (2009) Physical Review B, 80, Article ID: 220509.http://dx.doi.org/10.1103/PhysRevB.80.220509
- Igawa, K., Arii, A., Takahashi, Y., et al. (2009) Journal of Physics: Conference Series, 150, Article ID: 052075.
- Shein, I.R. and Ivanovskii, A.L. (2009) arXiv:0905.3126v1.
- Deemyad, S. and Schilling, J.S. (2003) Physical Review Letters, 91, Article ID: 167001.http://dx.doi.org/10.1103/PhysRevLett.91.167001
- Fratini, M., Poccia, N., Ricci, A., et al. (2010) Nature, 466, 841. http://dx.doi.org/10.1038/nature09260
- Grande, V.B., Muller-Buschbaum, Hk. and Schweizer, M. (1977) Zeitschrift fur Anorganische und Allgemeine Chemie, 428, 120. http://dx.doi.org/10.1002/zaac.19774280116
- Bollinger, A.T., Dubuis, G., Yoon, J., et al. (2011) Nature, 472, 458. http://dx.doi.org/10.1038/nature09998
- Fietz, W.H., Wassilew, C.A., Ewert, D., et al. (1989) Physics Letters A, 142, 300. http://dx.doi.org/10.1016/0375-9601(89)90334-4
- Budzioch, J., Jezierski, A., Ivanov, V., et al. (1999) Journal of Physics: Condensed Matter, 11, 8069.http://dx.doi.org/10.1088/0953-8984/11/41/310
- Schoenes, J., Schonenberger, C., Franse, J.J.M., et al. (1987) Physical Review B, 35, 5375.http://dx.doi.org/10.1103/PhysRevB.35.5375
- Knetsch, E.A., Menovsky, A.A. and Mydosh, J.A. (1994) Journal of Low Temperature Physics, 94, 307.http://dx.doi.org/10.1007/BF00754672
NOTES

1This problem was uncovered from My Ph.D. Supervisor Prof. H. R. Ott.


