Received 16 March 2014; revised 12 April 2014; accepted 8 May 2014

ABSTRACT

For the first time the vector differential equation of central motion of single electron in electric field of an atomic nucleus as in external central electric field is set up and solved. Here the following findings are reported. Each of single electrons of a part of atoms of atomic gas of hydrogen and a part of hydrogen-like ions in the form of a gas or a vapour revolves around corresponding atomic nucleus in a flat spiral which has an interior maximum of turns density. The distance between each of these single electrons and corresponding atomic nucleus increases while a speed of single electron decreases. Such motion of single electrons takes place with no expenditures of external energy and points to decays of foregoing parts of atoms and ions. The electric field strength of the atomic nuclei of atoms of atomic gas of hydrogen and hydrogen-like ions in the form of a gas or a vapour is inversely proportional to the distance between the atomic nucleus and the corresponding single electron by greater than the power of 3. Calculated cyclic frequency (rough value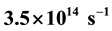) of revolution of the electron around the nucleus of atom of atomic gas of hydrogen (in interior maximum of turns density of the flat spiral), which moves at speed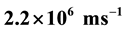, and central cyclic frequency of -line of Balmer series 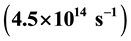have the same order of magnitude. This fact and line structure of experimental emission line spectra confirm the formation of all lines of these spectra by continuous slight emission of light front by single electrons. The formation of series of lines of emission line spectra is linked to repeated creations of atoms of atomic gas of hydrogen and hydrogen-like ions in the form of a gas or a vapour.

Keywords:

Atomic Gas of Hydrogen, Hydrogen-Like Ions, Slight Emission of Light Front by Single Electron, Emission Line Spectra

1. Introduction

Atomic gas of hydrogen (atomic hydrogen) and hydrogen-like ions in the form of a gas or a vapour have been used for experimental study of emission line spectra (see e.g. [1] ). Theory of these spectra was proposed by N. Bohr (1913) and developed in quantum mechanics and quantum electrodynamics.

However phenomena of atomic physics and optics have been described not only by quantum theory. Generally known example [1] is Cerenkov radiation (1934), which was interpreted on the basis of classical electrodynamics. This effect applies to slight emission of light front in the form of a conical surface by charged particles (for example, by electrons), passing through a transparent medium at a speed greater than the speed of light in that medium. According to [1] the effect is similar to that of a sonic boom when an object moves faster than the speed of sound.

In our time at the end of XX century the effect of substantial reduction of light speed in atomic gas of Na with the high atomic density was discovered [2] .

The discoveries of Cerenkov radiation and afore-named effect of substantial reduction of speed of light give ground for a new research of emission line spectra with such supposition. I have supposed that a speed of single electrons of atoms of atomic gas of hydrogen and a speed of single electrons of hydrogen-like ions in the form of a gas or a vapour are greater than the speed of light in electric field of corresponding atomic nuclei. Consequently, these single electrons, moving around atomic nuclei, simultaneously emit slight light front in the form of a conical surface (like Cerenkov radiation), i.e., form a line of emission line spectrum.

In order to establish fact of formation of a line and identify the way of formation of series of lines with slight emission of light front by single electrons a necessity appeared to find out the motion characteristics of single electron (especially the characteristics of its velocity) in electric field of an atomic nucleus. As far as I know these characteristics with a strict physical and mathematical argumentations have never been ascertained.

In the beginning of my work I had found out that motion of single electron around an atomic nucleus of a part of atoms of atomic gas of hydrogen and a part of hydrogen-like ions in form a gas or a vapour may be considered as plane. To define these motion characteristics I have set up the vector differential equation of central motion using the formulas for plane motion of a moving point (see e.g. [3] - [5] ). After transformations of this equation I have found equivalent to it final system of two scalar differential equations, which describe the changes of magnitude and direction of the velocity of single electron. On the basis of solution of final system the characteristics of plane motion of single electron were ascertained by me. In particular, I have found out that single electrons of foregoing parts of atoms of atomic gas of hydrogen and hydrogen-like ions in form a gas or a vapour move away from corresponding atomic nuclei, i.e., such parts of atoms and ions inevitably decay.

The ascertained characteristics, the slight emission of light front by single electrons which move around corresponding atomic nuclei, and also creation according to [4] of new atoms of atomic gas of hydrogen and new hydrogen-like ions in form a gas or a vapour define the formation of emission line spectra.

All novel results of the paper are formulated further in Section 12, Results.

2. Methods

This investigation is theoretical. The object of the investigation is plane motion of single electrons of a part of atoms of atomic gas of hydrogen and a part of hydrogen-like ions in form a gas or a vapour. A single electron is considered as a point, which has electric charge, mass and an initial speed, and moves on definable distance from an atomic nucleus.

The criterion of choice of mentioned parts of atoms and ions is the distance between single electron and an atomic nucleus. I have chosen this distance as enough big when it is possible to study the system: an atomic nucleus―single electron as two-body problem, while the motion of single electron may be considered as plane motion. Reducing two-body problem to one-body problem [4] , I passed to the question about definition of motion of single electron in electric field of an atomic nucleus as in external central electric field. According to such model I have set up the vector differential equation of central motion of single electron. This equation was transformed by me to equivalent system of two scalar differential equations which I have solved as extreme- value problem and obtained the answers to such questions:

-how does single electron move relative to atomic nucleus;

-does a speed of single electron change and what changes may be;

-what is a curve along which single electron moves;

-what is instantaneous angular rate of revolution of this electron around atomic nucleus;

-what is an electric field strength of an atomic nucleus as a function of the distance between atomic nucleus and single electron.

Additionally I have considered the process of formation of emission line spectra. This process is defined by motion of single electrons not only in separately taken atoms of hydrogen or hydrogen-like ions (during decays of such atoms and ions), but also in a gas or a vapour, which consist of such atoms or ions. I have compared results of this consideration with the results [6] of experimental study of emission line spectra.

3. Electric Field Strength of Atomic Nuclei

Let us elucidate, where in electric field single electrons of atoms of atomic gas of hydrogen and hydrogen-like ions in form a gas or a vapour may be found. Accordingly quantum mechanics an electron is located in an atom or molecule in a region of space, which is called orbital [1] . Taking into account this formulation of quantum mechanics one may affirm that distance 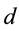between single electron and corresponding atomic nucleus of the part of foregoing atoms and the part of foregoing ions satisfies condition

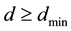(1)

where 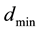is the distance to atomic nucleus which approximately equals to atom sizes (of the order of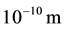) and is much more than nucleus sizes (of the order of) [1] . Consequently, on the distance 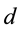we can consider an atomic nucleus as a point and its electric charge as a point charge.

Then vector 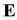of the electric field strength of an atomic nucleus may be written down in a simple form

(2)

where is the positive magnitude of the electric field strength of the nucleus (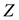is number of protons of the nucleus: if, the question is the electric field strength of atomic nuclei of atoms of atomic gas of hydrogen; if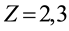, etc., the question is the electric field strength of atomic nuclei of corresponding hydrogen-like ions in form a gas or a vapour; is the function which depends on the distance only and is negative monotonic, i.e., such function, that decreases, as increases); is unit vector of direction of vector.

4. Coordinate Systems and Frame of Reference

Let mutually perpendicular axes, , (intersecting at the origin) of right-handed rectangular cartesian coordinate system are specified. Additionally cylindrical coordinate system is also specified and its cylindrical coordinates, , defined so that

(3)

where, , were rectangular cartesian coordinates of a point [3] .

I have studied the motion of single electron around an atomic nucleus (distanced from other the same nuclei) in inertial frame of reference. Taking into account condition (1) I have considered the motion of single electron in the scope of two-body problem: an atomic nucleus and single electron. According to [4] the center-of-mass system in two-body problem is inertial frame of reference. I have chosen just such frame of reference on the condition, that its center of mass was motionless. For that I had matched the point with this center of mass.

Also I had directed axis perpendicularly to plane of motion of single electron, because the motion of particles of two-body problem was plane in the center-of-mass system [4] . Further I have passed from two-body problem to one-body problem, consequently, I have considered the motion of single electron in electric field of an atomic nucleus as in external central electric field.

Thus, single electron moves at some initial speed along the plane curve, whose coordinates satisfy the system of parametric equations

(4)

where, , are rectangular cartesian coordinates of single moving electron as the functions of and in inertial center-of-mass system (is the arc length of the curve (4); is time); is the position vector of single moving electron; and are the initial and the finite values of time, respectively. (In this paper rectangular cartesian coordinates and the position vector of single electron as well their derivatives are often written without parameters and.) The functions of the system (4) have unique

continuous first derivatives with respect to and, and for (is the

unit vector of tangent to the curve (4); is the velocity of plane motion of single electron). The cylindrical coordinates of single electron as the functions of and in inertial center-of-mass system are, , and

. The cylindrical coordinate of single electron (see [4] ), or

(5)

because (,are mass of atomic nucleus and electron, respectively; is number of nucleons).

5. Acceleration of Plane Motion of Single Electron

Let us consider the acceleration of motion of single electron. I write down this acceleration in inertial center-of- mass system. Accordingly the second Newton’s law single electron accelerates in electric field of an atomic nucleus

(6)

where the acceleration vector and the unit base vector of cylindrical coordinate system are vector functions of and; is the charge of single electron; is positive magnitude of the electric field strength of an atomic nucleus in inertial center-of-mass system; is the function which depends on coordinate of single electron only and is negative monotonic, i.e., such function, which decreases as increases; interdependence of the functions and (see Equation (2)) is defined by equalities

.

6. Vector Differential Equation of Central Motion of Single Electron

According to [3] the indefinite integral

(7)

оf a suitable vector function is defined as the solution of the vector differential equation

(8)

which may be replaced by a set of differential equations for the components of; is a scalar parameter.

In Equations (7) and (8) I have changed by velocity of plane motion of single electron in inertial center-of-mass system; by acceleration vector of single electron (see Equation (6)) and did a scalar parameter by time. Then changed Equation (8) is the vector differential equation of central motion of single electron

(9)

The Equation (9) may be solved after its replacement accordingly [3] by the set of two differential equations for physical components of in cylindrical coordinate system. From the solution the characteristics of and suitable function (according to Equation (6)) may be found. But first of all I have made necessary transformations of Equation (9) taking into account that both and are vector functions of the arc length of the curve (4) and time.

7. Transformations of Vector Differential Equation (9)

According to [3] - [5] I have decomposed derivative with respect to time into tangential and

normal components of acceleration, i.e., transformed Equation (9) to the form

(10)

where is the rate of change of speed of single electron with respect to (the dot above a

letter indicates differentiation with respect to time); is the positive instantaneous angular rate of turn around instantaneous position of axis, which is matched with; is the unit binormal vector to the curve (4) in each its point.

Then I have transformed Equation (10)

(11)

In Equation (11) replacement of angular rate by other characteristics of plane motion of single electron

is expedient. According to [3] may be represented as or may be written down thus

(12)

where is curvature of plane curve (4) in each its point; is the angle between the tangent to this curve and the radius-vector, which at each point of a curve (4) is given by (in this paper I have de-

fined the angle in plane by cylindrical coordinates, as polar coordinates; then curve is plane curve (4)); is instantaneous angular rate of revolution of the position vector of single electron around instantaneous position of axis.

Decomposition of derivative with respect to time into tangential and normal components of accele-

ration is illustrated by Figure, that gives the graphic idea about the plane motion of single electron in electric field of an atomic nucleus.

On this Figure 1is shown, in particular, that angle is acute. It means coordinate of this electron increases during its motion.

Further, according to [4] I have decomposed into two physical components along the local base vectors and (is not shown on Figure):

(13)

Here the directional derivative, where is the angle (not shown on Figure) between the unit vectors and (findings of derivative and the angular rate see in Apps. A and B, respectively).

Then I have substituted in Equation (11) from Equation (6), from the second Equation (12), from Equation (13), and also replaced in Equation (11) the unit vector by the local base vector, which is equal to

(14)

Let us rewrite the vector differential Equation (14) in that way

(15)

Now I calculate the vector products and:

(16)

(17)

Let us substitute results of Equations (16) and (17) into Equation (15):

(18)

Obtained Equation (18) is equivalent to Equation (9).

8. Finding of Final System of Two Scalar Differential Equations

I have replaced the vector differential equation (18) by the set of two differential equations for physical components of (see Equation (13)) in cylindrical coordinate system

(19)

The set of Equations (19) may be written down in scalar form

(20)

After elementary transformations of the set (20) I have found the derivatives, , and also conditions for them (see App. C), and represented these derivatives as final system of two scalar differential equations on general conditions:

(21)

In the system (21)

(22)

(23)

In Equations (21)-(23) the quantities, (and thus also), , , , and, consequently, deriv-

atives, depend on while depends on time.

The values of the function change in the range

(24)

where is the instant of time of creation (initial value of time) and is the instant of time of decay (finite value of time) of the part of atoms of atomic gas of hydrogen and the part of hydrogen-like ions in form a gas or a vapour.

The final system (21) is equivalent to Equation (9) and describes the revolution of single electron around instantaneous position of the center of mass of foregoing parts of atoms and ions. Instantaneous angular rate (see Equation (23)) may be also considered as instantaneous angular speed of revolution of single electron around an atomic nucleus (not only around instantaneous position of the center of mass), because according to Equation (5). The first equation of system (21) describes changes with respect to of magnitude of velocity of single electron, and the second one describes the changes with respect to of direction of this vector, which is specified by the angle.

9. Solution of Final System (21) As Extreme-Value Problem [3]

To solve the system (21) as extreme-value problem it is necessary to find the conditions which maximize the angle: condition for values of angle and condition for values of the functions, ,

and also derivative.

In the beginning according to [3] let us write down the conditions for the existence of interior maximum and interior minimum of angle:

a) if exists for, then can be a (necessarily interior) maximum or minimum only if

has a stationary value for, i.e.,

(25)

Here the first derivative is the second differential equation of system (21) and value is interior point of the range (24);

b) if and has the second derivative for, then on condition

(26)

is interior maximum, and on condition

(27)

is interior minimum.

(Finding of second derivative, where the derivative from the first differential equation of sys-

tem (21) is also used, see in App. D.)

According to condition (25) and the second differential equation of system (21) I have obtained the equality

(28)

which relates a value with corresponding values of other quantities of this equality.

Then according to App. D I have determined the value of second derivative for:

(29)

Taking into account the equality (28) in Equation (29) I have obtained

(30)

Accordingly condition (27) I have investigated the function for availability of interior minimum. From Equation (30) one can see, that condition (27) takes place, if

(31)

because in the paper.

Consequently, according to Equation (31) condition (27) takes place in two cases:

1) if, i.e.,

(32)

and, i.e.,

(33)

2) and vice versa, if, i.e.,

(34)

and, i.e.,

(35)

Both these cases have no physical sense. In the case 1) values of derivative (see inequality (33))

may be neither zero nor positive, because the function may be neither constant nor increasing by definition. In the case 2) angle may not take such values (see condition (34)), because these values are out the range of values of angle. Consequently, interior minimum of the function is impossible.

Further I have investigated the function for availability of interior maximum according to condition (26). From Equation (30) one can see that the condition (26) is fulfilled, if

(36)

because, as were pointed out before.

Consequently, accordingly Equation (36) the condition (26) takes place in such two cases:

1) if, i.e.,

(37)

and, i.e.,

(38)

2) and vice versa, if, i.e.,

(39)

and, i.e.,

(40)

Investigating interior maximum of the function, I have considered the case 2) at first. This case has no

physical sense, because values of derivative (see inequality (40)) may be neither zero, nor positive

(the function may be neither constant, nor increasing, as we had found out). Additionally, the case 2) has no physical sense because values of angle (see condition (39)) are out the range of values of angle.

Let us consider the case 1). From condition (37) one can see the values of angle may be coincided

with the values of angle. According to condition (38) values of derivative may be negative on-

ly. That corresponds to definition of the function which is decreasing function. Consequently, the case 1) has physical sense and interior maximum of angle takes place, i.e., by conditions (37) and (38) the angle maximizes.

10. Motion Characteristics of Single Electron as Results of Maximization of Angle

Maximization of angle let to find the characteristics of revolution of single electron in the form of description or functions of general form, etc. For example, the function of speed of single electron may be found only as negative monotonic function.

From the range of values of angle (see App. C) follows that as a result of maximization of this angle

(41)

It means, that for an suitable function the unit vector is directed at acute angle to the unit vector (see Figure). So long as single electron revolves around atomic nucleus in a plane, it moves in flat spiral, that untwists. Consequently, during the motion of single electron its coordinate increases, therefore the distance between this electron and corresponding atomic nucleus increases too. As a result of such motion single electron moves away from atomic nucleus. It means, the part of atoms of atomic gas of hydrogen and the part of hydrogen-like ions in form a gas or a vapour inevitably decay (without any expenditure of external energy).

For the range of values of angle by definition of angle and according to condition (37). Therefore, and

. (42)

From condition (42) and the first differential equation of system (21) I have concluded, that

, (43)

i.e., speed of single electron only decreases during its revolution around an atomic nucleus. The inequality (43)

means also, that tangential component of acceleration of single electron is directed against (i.e., against), because the derivative. Consequently, the direction of motion of single electron, that is il-

lustrated by arrow on the curve (4) (see Figure), is confirmed by solution of system (21).

There are two reasons of decrease of speed of single electron: slight emission of light front (see 1. Introduction) and self-ionization of atom or ion, which is contained single electron. If both these reasons lead to a small

decrease of speed of single electron, then one may assign, from which.

Now one may explain, how interior maximum of turns density of flat spiral is formed. Such maximum is connected with maximum of angle. Increase of angle to maximum value causes to:

-increase of turns density of flat spiral;

-approach of turns form of this spiral to circle form.

So long as for the angle has interior maximum, the turns density of spiral has also interior maximum for.

Let us consider the characteristics of revolution of single electron around an atomic nucleus in the interior maximum of turns density of flat spiral. According to Equation (23) value of instantaneous angular rate

(44)

because value.

Now let us consider equality, that I have obtained from the relation (28):

(45)

The right side of Equation (45) approximately equals to value of angular rate accordingly Equation (44). Consequently, for value we can obtain one new formula

(46)

In maximum of turns density of spiral the form of these turns approaches to the form of a circle, consequently the motion of single electron may be characterized by cyclic frequency. Dividing (44) and (46) by I have found correspondingly

(47)

(48)

In Equations (47) and (48) is cyclic frequency of revolution of single electron around an atomic nucleus in maximum of turns density of spiral, which is approximately equals to cyclic frequency of revolution of this electron in a circle of radius at constant speed.

At last let us consider the result of maximization of angle about the electric field strength of an atomic nucleus. Proceeding with the inequality (38) I have proved, that the function is proportional to

and the power (the proof see in App. E).

Let us pass from the function to the function (see 5. Acceleration), where. So long as, the electric field strength of an atomic nucleus (on condition (1)) is inversely proportional to the distance by greater than the power of 3.

11. Formation of Separate Line and Series of Lines of Emission Line Spectra

A. Formation of separate line

In my supposition (see Section 1. Introduction), a separate line is formed by single electron when it moves around an atomic nucleus and emits a slight light front in the form of a conical surface simultaneously. However such line is formed not by one single electron, but by many single electrons of the part of atoms of atomic gas of hydrogen (and the part of hydrogen-like ions in form a gas or a vapour). During the formation of separate line each single electron revolves around corresponding atomic nucleus in interior maximum of turns density of the spiral. Approximate value of cyclic frequency of revolution of such electrons may be determined by Equations (47) and (48).

From each of these single electrons the light front comes to spectral device one time per a turn of single electron around an atomic nucleus. Therefore central cyclic frequency of separate line equals to corresponding value, i.e.,

(49)

The formation of separate line is connected with the interior maximum of turns density of flat spiral and therefore this line has the form of a top which is confirmed in experiment [6] . Such form of the line indicates, that decrease of speed of single electrons is caused, in particular, by slight emission of light front.

B. Formation of series of lines

Formation of series of lines takes place, when the same single electrons move consecutively through electric fields of several atomic nuclei and simultaneously emit slight light front. Such motion of single electrons is possible because of the decays of the part of atoms of atomic gas of hydrogen (or the part of hydrogen-like ions in form a gas or a vapour) and also because of small decrease of a speed of single electrons.

Let us consider formation of series of lines using as example Balmer series. After creation of primary atoms of atomic gas of hydrogen (for example, from a vapour of water [6] ) each electron of the part of these atoms distances from corresponding atomic nucleus in flat spiral and forms the first line, i.e., -line of Balmer series. Accordingly Equations (48) and (49) central cyclic frequency of this line may be defined as

(50)

where inferior index denotes the quantities which are concerned to -line; is value of the electric field strength of atomic nuclei of primary atoms of atomic gas of hydrogen in maximum of turns density of flat spiral, i.e., for; is value of speed of the electrons in maximum of turns density of flat spiral.

After formation of -line the electrons move away from electric fields of the part of primary atoms of atomic gas of hydrogen at speed, which decreases a little. Thus, the part of primary atoms of atomic gas of hydrogen decays to free moving atomic nuclei and free moving electrons. According to the theory of central forces [4] free moving atomic nucleus captures the suitable free moving electron and creates secondary atom of atomic gas of hydrogen. The electrons of the part of secondary atoms form -line of Balmer series and also move away from secondary atoms, i.e., the part of secondary atoms also decays. By analogy with definition of (see Equation (50)) I have found central cyclic frequency of -line of Balmer series

(51)

where inferior index denotes the quantities which are concerned to -line; is value of the electric field strength of atomic nuclei of secondary atoms of atomic gas of hydrogen in maximum of turns density of flat spiral, i.e., for; is value of speed of the electrons, which form - line, in maximum of turns density of flat spiral.

By analogy with considered formation of - line also -, - and other lines of Balmer series (except last lines of exceptionally long Balmer series) are formed.

From studying emission line spectra it is known [1] [6] , that for series of lines central cyclic frequency of emission of every next line is greater than corresponding frequency of previous line. I explain this fact, using also Balmer series as example. So long as all lines of a series are formed by the same single electrons, speed of which decreases during formation of lines, then. Further, the less is the speed of the electrons

during creation of secondary atoms (in the way of capture [4] ) the more is value. Consequently,. Both mentioned inequalities define, that accordingly Equations (50) and

(51). But intensities of lines decrease as their ordinal number increases. That may be explained by decrease of probability of capture of the electrons with atomic nuclei because of decrease of quantity of these electrons and nuclei (in particular, because of scattering). From this explanation it is clear, that way of formation of series of lines is linked to repeated creations of atoms of atomic gas of hydrogen (and hydrogen-like ions in form a gas or a vapour) after decays of such atoms and ions.

Formation of other series of lines both atoms of atomic gas of hydrogen and any hydrogen-like ions in form a gas or a vapour takes place like formation of Balmer series. But, in my opinion, the first line of each such series (except the first lines of main series of hydrogen-like ions) is formed with the help of electrons of gas discharge, if a speed of these electrons may be assigned in experiment. Probably, last lines of exceptionally long Balmer series are formed also by the electrons of gas discharge.

Let us illustrate, how just separate line is formed by the electrons at assigned speed.

C. Formation of separate line by electrons at assigned speed

Firstly I have considered the following. If atomic gas of hydrogen is bombarding by the electrons with assigned energy 13.6 eV, these electrons will move through electric fields of free moving atomic nuclei (which are in atomic gas of hydrogen) at assigned speed. These electrons will be captured by free moving atomic nuclei, i.e., new atoms will be created. If current of the electrons of bombardment is intensive, then in a result of decays of newly-created atoms intensive series of lines is formed. Accordingly Equations (48), (49) central cyclic frequency of the most intensive line of this series is determined by the speed. This speed approximately equals to, because during the spiral in electric field of atomic nucleus the speed of the electron decreases comparatively little. Frequency of the most intensive line coincides with central cyclic frequency of -line of Balmer series, i.e.,. From this coincidence one can conclude, that speed of the electrons in primary atoms of atomic gas of hydrogen (before bombardment) approximately equals to.

Then I have made such calculation. Using Equation (47) and the value I have obtained the value, which corresponds to frequency of line. To calculate I have used

numerical value which is in 10 times more than value of size of atoms [1] , because during emission of light front in atom of atomic gas of hydrogen the coordinate of the electron increases. Thus, .

The calculation by Equation (47) gives. By the order of magni-

tude the value equals to the value of central cyclic frequency of -line of Balmer series, which I have obtained as the result of division of speed of light in vacuum by the length of wave [1] . The equality of the orders of magnitudes of these frequencies confirms of a line formation with continuous slight emission of light front by the electrons during their motion around corresponding atomic nuclei. Difference of the values and may be explained by impossibility to determine the value of exactly.

12. Results

In the paper the model of motion of single electron in electric field of an atomic nucleus as in external central electric field is developed. During development of this model I have found out, that after creation of atoms of atomic gas of hydrogen and hydrogen-like ions in form a gas or a vapour the motion of single electrons of the parts of mentioned atoms and ions one may consider as plane motion. To define the characteristics of such motion of single electron the vector differential equation of central motion was set up. As a result of solution of the final system of differential equations, which is equivalent to aforementioned vector differential equation, I have found the following.

Not a single electron of foregoing parts of atoms and ions “falls” on corresponding atomic nucleus but only moves away from it, revolving around the nucleus along flat spiral and continuously emitting a slight light front in the form of a conical surface. The spiral has the interior maximum of turns density. Moving away from the nucleus, each single electron decelerates with its electric field and the speed of single electrons decreases slightly. As a result single electrons move away from electric fields of atomic nuclei with no expenditures of external energy. I have proved, that the electric field strength of an atomic nuclei of atoms of atomic gas of hydrogen and hydrogen-like ions in form a gas or a vapour for a point of single electron location (accordingly condition (1)) is inversely proportional to the distance between the corresponding atomic nucleus and single electron by greater than the power of 3. I have also found relations (47) and (48) for calculation of cyclic frequency of revolution of single electron around an atomic nucleus in maximum of turns density of flat spiral.

One can see in the paper, that calculated cyclic frequency (rough value) of revolution of the electron around the nucleus of atom of atomic gas of hydrogen (in the interior maximum of turns density of flat spiral), which moves at speed, and central cyclic frequency of -line of Balmer series have the same order of magnitude. This fact confirms the formation of a line with continuous slight emission of light front by single electrons. And what is more, slight emission of light front defines the formation of all lines of emission line spectra, i.e., their line structure. The way of formation of series of lines is linked to repeated creations of atoms of atomic gas of hydrogen and hydrogen-like ions in form a gas or a vapour.

13. Discussion

The results of the paper may be conditionally classified into two groups. The first group of results has a bearing on motion characteristics of single electron, the second one applies to the formation of emission line spectra.

Using the second Newton’s law, I have ascertained the motion characteristics of single electrons of the part of atoms of atomic gas of hydrogen and the part of hydrogen-like ions in form a gas or a vapour. Ascertained characteristics mean these parts of atoms and ions inevitably decay, that was unknown before. During their decays emission of light front and self-ionization take place, which need a small expenditures of internal energy, i.e., expenditures of external energy are not necessary (according to currently accepted opinion, expenditures of definite external energy are necessary, that is incorrectly).

Also I have proved, that the electric field strength of an atomic nucleus (in considered region of electric field) is inversely proportional to the distance from nucleus by the power greater than 3. It means, that interaction between single electron and electric charge of an atomic nucleus is not described by Coulomb’s law.

Note that both mentioned results: decays and condition are interconnected, because they follow from two solutions of system (21). The electric field of an atomic nucleus may not retains single moving electron on finite distance from this nucleus, when the power greater than 3. Therefore single electron moves away from atomic nucleus, revolving in flat spiral. These conclusions do not contradict known results of the theory of central forces [4] . According to this theory it is necessary to fulfill such condition for stable motion of a particle around motionless point, which attracts this particle. The power of inversely proportional dependence of force on the distance between the particle and the motionless point must be less than 3. Therefore for stable motion of single electron around an atomic nucleus the power must be less than 3 too.

In a future research it is necessary to elucidate why the atoms of hydrogen which are connected in chemical compounds (for example, in molecules of water) are stable, whereas the atoms of atomic gas of hydrogen decay, and their electrons emit light front in this time. To approach the answers to these and, perhaps, other questions, I have made the following. From Equation (50) when I have found the formula to determine the electric field strength inside of atoms of atomic gas of hydrogen

(52)

where all quantities are known:, ,

,. The conversion factors (for SI and CGS units) are known too:,. Taking into account these factors I have determined

For atomic nucleus with which is more than 1 the electric field strength is still more. Probably the great value of the electric field strength of any atomic nucleus is the factor that causes reduction of speed of light in these fields to level, that is less, than speed of single electron. On such condition single electron emits light front (see 1. Introduction), revolving around an atomic nucleus along flat spiral, which untwists. If we decrease both the electric field strength, which acts on single electron, and the corresponding power, then emission of light front may disappear and single electron may stably revolve on finite distance from atomic nucleus. Corresponding decreases may be simultaneously caused with electric field of additional electron (or electrons).

Let us discuss now the second group of results of the paper?the formation of emission line spectra. I have shown, that all lines of these spectra are formed with slight emission of light front by single electrons. The hypothesis of slight emission of light front is confirmed by line structure of these spectra, which was discovered in experiments.

In future research it is necessary to ascertain, in particular, the values of frequency of revolution of single electron around atomic nucleus of atoms of atomic gas of hydrogen and hydrogen-like ions in form a gas or a vapour (in maxima of turns density of spiral) as function of values of speed of this electron in mentioned maxima.

14. Conclusions

In conclusion such statements may be added.

The second Newton’s law may be applied to define the motion characteristics of single electron in electric field of an atomic nucleus.

Coulomb’s law does not describe the interaction between electric charges of single electron and an atomic nucleus.

Emission line spectra are formed with slight emission of light front by single electrons during their revolution around corresponding atomic nuclei.

Energy of decays of the part of atoms of atomic gas of hydrogen and the part of hydrogen-like ions in form a gas or a vapour may be used in practice.

Cite this paper

Ivan AntonovychStrilets, (2014) Motion Characteristics of Single Electrons of Atoms of Atomic Gas of Hydrogen and Single Electrons of Hydrogen-Like Ions in Form Gas or Vapour during Decays of Such Atoms and Ions. Emission Line Spectra. Journal of Modern Physics,05,1302-1320. doi: 10.4236/jmp.2014.514131

References

Appendixes

Appendix A: Finding of Directional Derivative

If the direction of motion of single electron is assigned by the unit vector of tangent to the curve (4), then according to [3] :

(A1)

where (nabla) is the linear operator. In terms of rectangular cartesian coordinates is defined by

(A2)

where, , are the unit vectors, directed along the, , axes, respectively.

According to the rules for operations with the operator nabla I have obtained

(A3)

Let us substitute the result (A3) into Equation (A1)

(A4)

where is the angle between the unit vectors and; the values of angle, as angle, are positive.

The sign of directional derivative indicates the motion of single electron relatively the point. If

, then the electron moves away from the point, and vice versa, if, then the electron approaches to the point.

Appendix B: Finding of Instantaneous Angular Rate

Accordingly [3] in terms of polar coordinates, the distance element is given by

(В1)

Let us divide Equation (В1) by (is time)

(В2)

Taking into account in Equation (В2), that, and, one may written down

(В3)

From Equation (В3) I have obtained instantaneous angular rate of revolution of single electron around instantaneous position of the point (see Figure) during the electron motion in the plane:

(В4)

In this paper, as were mentioned. The sign “+” before the square root (see Equation (В4)) means.

Appendix C: Finding of Derivatives and

I have divided the first differential equation of the set (20) by, the second one divided by , and obtained

(С1)

Then I have added the first differential equation of the set (С1) to the second one

(С2)

and multiplied differential equation (С2) by:

(С3)

The left side of differential equation (С3) is equal to according to Equation (В3). Taking into account

Equation (В3) in Equation (С3) I have found after elementary transformation of Equation (С3):

(С4)

Then I have multiplied the first differential equation of the set (20) by and the second one multiplied by:

(С5)

I have subtracted the first differential equation of the set (С5) from the second one

(С6)

I have multiplied differential equation (С6) by, and taken into account in it Equation (В3):

(С7)

After elementary transformations of Equation (С7) I have found derivative

(С8)

Let us consider the ranges of values of some quantities that contains Equations (C4) and (C8). The positive

angle changes in the range by definition. The values, are defined by the relation. If this relation is minimum, then angle is minimum too. If the relation is as great as possible, the angle equals to. The positive angle changes in the range by definition. Differential

Equations (С4) and (С8) have the same conditions:

(С9)

If we take into consideration, , , , , then conditions for differential Equations (C4), (C8) can be written down as

, , , ,. (С10)

Appendix D: Finding of Second Derivative

(D1)

Let us substitute the derivative from Equation (С4) into Equation (D1)

(D2)

Let us transform Equation (D2)

(D3)

Appendix E: Finding of Function, That Satisfies Inequality (38)

At the beginning I have solved the equation, which is connected with inequality (38). To make that, in inequality (38) I have replaced the sign “<” by sign “=” the value replaced by the parameter, the function replaced by auxiliary function:

(Е1)

Separating variables in differential Equation (Е1), I have integrated it with definite conditions, :

(Е2)

i.e.,

(Е3)

or

(Е4)

The function (Е4) is the solution of differential Equation (Е1), that I have obtained from inequality (38). If we

substitute the function (where is real number) in inequality (38),

we will obtain. It means, that the function satisfies inequality (38) for, if, i.e.,

(E5)

and is the function, that must be found.