Journal of Modern Physics
Vol.4 No.12(2013), Article ID:41152,8 pages DOI:10.4236/jmp.2013.412200
Speed Testing of the Graviton and the Movement Track of Graviton in the Spiral Galaxy
Yunqu Yuan, Huilong Guan, Changping District, Beijing, China
Email: luopingan6362@sohu.com
Copyright © 2013 Pingan Luo. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received September 17, 2013; revised October 19, 2013; accepted November 16, 2013
Keywords: Graviton; Graviton Speed; Movement Track; Spiral Galaxy; M51; Upper Limit of Speed; Super Velocity of Light
ABSTRACT
According to a series of hypothesis, for the spiral galaxy, a mathematical equation of the graviton movement track is built, it is also the central curve of the nebulae density distribution, which offers the method to measure the moving speed of the graviton. Using the observed images of the M51 galaxy, it confirms that the graviton movement curve in the spiral galaxy conforms to the image,  QUOTE
QUOTE 
![]() QUOTE
QUOTE 
![]() is a constant. It points out that by measuring the rate of angular motion of the equivalent center in the galaxy, the real speed of the graviton can be estimated. Under the measuring condition of the M51,
is a constant. It points out that by measuring the rate of angular motion of the equivalent center in the galaxy, the real speed of the graviton can be estimated. Under the measuring condition of the M51, . The theory presented in this article also helps to calculate the rotation speed of a galaxy, provided the graviton speed is known for certain. With the model in this article and fitting data from the observation images of M51 galaxy, the guess which says “the moving speed of graviton is a constant” is supported unprecedentedly by observation data. It is for the first time that the upper limit of graviton speed, i.e. no more than
. The theory presented in this article also helps to calculate the rotation speed of a galaxy, provided the graviton speed is known for certain. With the model in this article and fitting data from the observation images of M51 galaxy, the guess which says “the moving speed of graviton is a constant” is supported unprecedentedly by observation data. It is for the first time that the upper limit of graviton speed, i.e. no more than  QUOTE
QUOTE 
![]() QUOTE
QUOTE 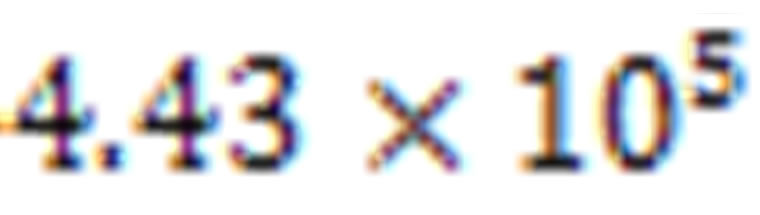
![]() times of light speed, is obtained from observation data. At the same time, the paper puts forward one possible way that the lower limit of graviton speed may be measured. And a new idea also brought forward in the paper is that the rotational angular velocity w of the equivalent center which plays an important role in a spiral galaxy may be measured according to the observed data of the thickness of galactic center of the spiral galaxy.
times of light speed, is obtained from observation data. At the same time, the paper puts forward one possible way that the lower limit of graviton speed may be measured. And a new idea also brought forward in the paper is that the rotational angular velocity w of the equivalent center which plays an important role in a spiral galaxy may be measured according to the observed data of the thickness of galactic center of the spiral galaxy.
1. Introduction
On September 22, 2011, the website of the American Cornell University [1] and the website of the British Nature magazine [2] reported that the European researchers found out the unexplainable phenomenon of the superluminal velocity of the neutrino. T. Adam [1] and others pointed out:
1) During the distance of 730 kilometers, the observed moving speed of neutrino is 60 ns faster than the light, which means it runs 6 more kilometers in a second;
2) The moving speed of the neutrino is related to its energy.
In June 2012, scientists of European Organisation for Nuclear Research clarified: results of prior experiments were incorrect. Problems occurring at the cable connection of experimental equipment resulted in the error [3].
According to Albert Einstein’s Special Theory of Relativity, light speed is the limit speed in the universe; nothing can exceed the light speed. Indeed, no particle faster than light has been detected so far due to the constriction of current experimental conditions. But this neither means that particles of this kind are nonexistent nor ensures that they won’t be discovered in the future. If it is true that the moving speed of XX particle is faster than the light speed, then the classical theory of Einstein’s shall be revised. If the phenomenon that the moving speed of XX particle is faster than the light speed is truly the case, then will the speed of graviton also exceed the light speed? How to measure? Is there any experimental data to support it?
The answers to the above questions involve the dark clouds shrouded on the modern physics, they are: where is the graviton? what are the properties? what is the speed? And why cannot be found in experiment? Whether the speed of graviton exceeds the light speed or not, the physicists know the property of graviton will have a great influence on the construction of the whole physical theories. Today, when graviton is also undetectable, it is not appropriate either to simply believe that the moving speed of graviton equals to or never exceeds light speed. Due to the weak gravity, it cannot be found with the current experimental conditions. It may be better if we switch the study angle of graviton to the astronomy field.
To study the speed of the graviton, we hope to find a spiral galaxy and use its observing data to do deeper study. Document [4] points out, in the near more than 400 galaxies, according to the Hubble’s classification means, most of the galaxies have the oval or eddy shape structure, among which only about 3% of the galaxies have the irregular form. According to the related documents, it can be seen that the M51 galaxy is a representative galaxy for the observing data are quite complete. Document [5] summarized a series of recent international achievements by studying the M51. It clearly pointed out that the projector distance from the M51 center to the companion NGC5195 (or M51b) is 15.5 kpc.
2. The Movement Track of the Graviton in the Spiral Galaxy
Under some assumptions he proposes without compulsorily using the hypothesis that light speed is the upper limit of all particles movement, the writer of this article puts forward the mathematical equation of the graviton movement and brings up with the method of using the astronomy measuring result to measure the graviton speed for the first time, and published on the J. Modern Physics, Vol. 3, No. 4, 2012 [6].
Hypothesis:
1) In any of the inertial reference system, the velocities of gravitons are the same in different directions shottheory of the unchanged graviton speed. i.e.: the graviton has the properties similar to the photon.
2) Spin velocity of a spiral galaxy equivalent centrebody is a constant rotational angular velocity w, radian/s as its unit. Please be noted that there may be a plus or minus due to different direction of spinning axis.
3) In this spiral galaxy, gravitons launched outwards mostly come from equivalent centrebody of the galaxy and form main part of the galaxy’s gravitational field. Other stars are in this field.
4) Launching of gravitons are independent to each other.
5) Possible interaction between gravitons during their motion can be omitted.
6) In this galaxy, perpendicular lines between outerring stars along motion traces of gravitons are normal distribution.
Then the motion trace of the graviton shall satisfy Formula (1), and get the graviton speed by Formula (2).
 (1)
(1)
 (2)
(2)
where in:
 —graviton moving speed (m/s), or (light year/s);
—graviton moving speed (m/s), or (light year/s);
q—the rotation angle of the galaxy equivalent center (radian);
q0—the initial rotating angle of the galaxy equivalent center (radian);
r—the distance of graviton away from the galaxy center (m), or (light year);
w—during spiral galaxy, the rotational angular speed of the equivalent center which plays an important role (radian/s), may be faster than the optically observed rotational angular speed of the galactic center of the spiral galaxy, but the lower limit of the graviton speed can be determined according to the rotational angular speed of the galactic centersurface.
This theory believes that the distribution of the gravitational field is built by the gravitation property of the galactic center in the galaxy. The stars on the spiral periphery of the galactic center do not have a great influence on the distribution of the gravitational field of the spiral galaxies. However, the stars’ location in the gravitational field of the spiral galaxies will be affected by the distribution of the gravitational field of the spiral galaxy, which means the shape of the spiral arm in the spiral galaxy indicates the distribution status of the gravitational field for the spiral galaxy. This status is similar to the experiment of using the petty scrap iron to trace the distribution of the magnetic lines of force for the U shape/ horse hoof shaped magnet.
In Formulas (1) and (2), w is not the rotational angular speed of the spiral arm of the galaxy and those stars in the spiral arm around the center of galaxy, but the autorotation angular speed of the spiral galaxy equivalent centrebody which plays an important part in the building process of the gravitational field of the spiral galaxy. The part which plays an important role in building gravitational field of galaxy in the galactic center is defined as the equivalent centrebody of this spiral galaxy. Because the galactic center is not the rigid body, the internal rotational angular speed is faster than that of the surface, thus, there may be a multiple relation between the autorotation angular speed of the equivalent centrebody in the galactic center of the spiral galaxy and the surface rotational angular speed. With the analogy of atom movement, the observed galactic center surface of the galaxy is similar to the shape of the K layer electron cloud rotating around the atomic nucleus which embraces the real equivalent centrebody; the equivalent centrebody of the galaxy is similar to the atomic nucleus.
The feature of this theory (see the previous hypothesis 1) and 2)) conforms to the Archimedes’ spiral line in mathematics [7]. In another word, the physical model of this theory can be abstracted to a mathematical model, which will be the model of “Archimedes’ spiral line”.
Document [7] describes the Archimedes’ spiral line: “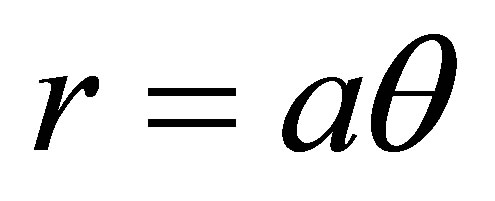 , the curve is the trace drawn by a moving point which moves along a ray with a constant speed v, and the ray moves around the pole point o with a fixed angular speed of w. The proportionality coefficient is
, the curve is the trace drawn by a moving point which moves along a ray with a constant speed v, and the ray moves around the pole point o with a fixed angular speed of w. The proportionality coefficient is .”
.”
To summarize, the measuring value of the ratios of graviton moving speed to the autorotation angular speed of the equivalent center in the spiral galaxy can be obtained by using the observed astronomical results (such as M51) and using the least square. Because the size of the sun is much smaller than that of equivalent center in the galaxy which is an important part in the gravitational field of the M51, we can estimate that the autorotation angular speed of the sun surface is much larger than that of the equivalent center in the galaxy which is an important part in the gravitational field of the M51. Therefore, we can use the autorotation angular speed of the sun surface to estimate the upper limit of the autorotation angular speed for the equivalent center in the M51 galaxy; and the rotating speed of the galactic center surface of the M51 galaxy to estimate the lower limit of the autorotation angular speed for the equivalent center in the M51 galaxy. And then get the upper and lower limit of the graviton moving speed.
3. The Handling Method of the Observed Pictures of M51 Galaxy
From some professionally organized astronomy websites, the observed pictures of the M51 with different resolutions can be obtained. Due to the limit of the operation conditions of my computer, I chose the picture with the resolution of 1854 ´ 1830, see Figure 1.
3.1. The Distance Indicated by the M51 Image and the Selection of the Processing Area
Use the projector distance 15.5 kpc from the center of M51 to the companion NGC5195 (or M51b) provided by the document [5] to scale the distance in Figure 1 (see Figure 2). The distance calibration factor k is:


Figure 1. Observed pictures of M51 galaxy. The pixel of the image is: 1854 ´ 1830.
Due to the limits of the data processing software, the data matrix cannot be too large. For convenience, the companion and outward flange of the Figure 1 can be cut by using the picture processing software. The result is as Figure 3, (the pixel of the image turns to 1084 ´ 836).
3.2. The Division of the Spiral Arm Area before the Image of M51 Is Changed
When handling the data, the coordination of the data in image M51 shall be changed in order to compare the data before and after changing. First, draw two grouping isolation curves 2 and 3 on Figure 3 by hand and use a circle similar curve 1 to embrace the galactic center of M51, see Figure 4.
3.3. Change the Data of the Image to the System of Polar Coordinates
Set the origin point in the galactic center of the M51 galaxy; the positive direction of the shaft of rotational angle q is rightwards, the anti-clockwise direction is a positive angle; the radius r is the positive direction. Change the color in Figure 4 to grey, and then change the coordination. The image changed to the plane of r - q, see Figure 5.
In Figure 5, the origin point in the r - q plane is in the lower left corner; the r direction is the ordinate axis, upward is positive; the q direction is the horizontal axis, rightward is positive; please be specially noted that, the negative data of the q angle is translated 2p to be put into the fourth quadrant, see the curve 3 in the lower right corner of. Figure 6 clearly indicates the corresponding

Figure 2. Set the distance scale of the M51 galaxy image.

Figure 3. The main galaxy image of M51 used in the data processing subsequently. The pixel of the image is: 1084 ´ 836.

Figure 5. In the r - q plane of the M51 galaxy image, the curves 1, 2, 3 are corresponding to the related curve in Figure 4. (Note: the space interval of the rotational angle q (the horizontal axis) is [0, 2p], unit is 0.01 radian; the unit of r is the same as Figure 3. The pixel of the image is: 629 ´ 846.)
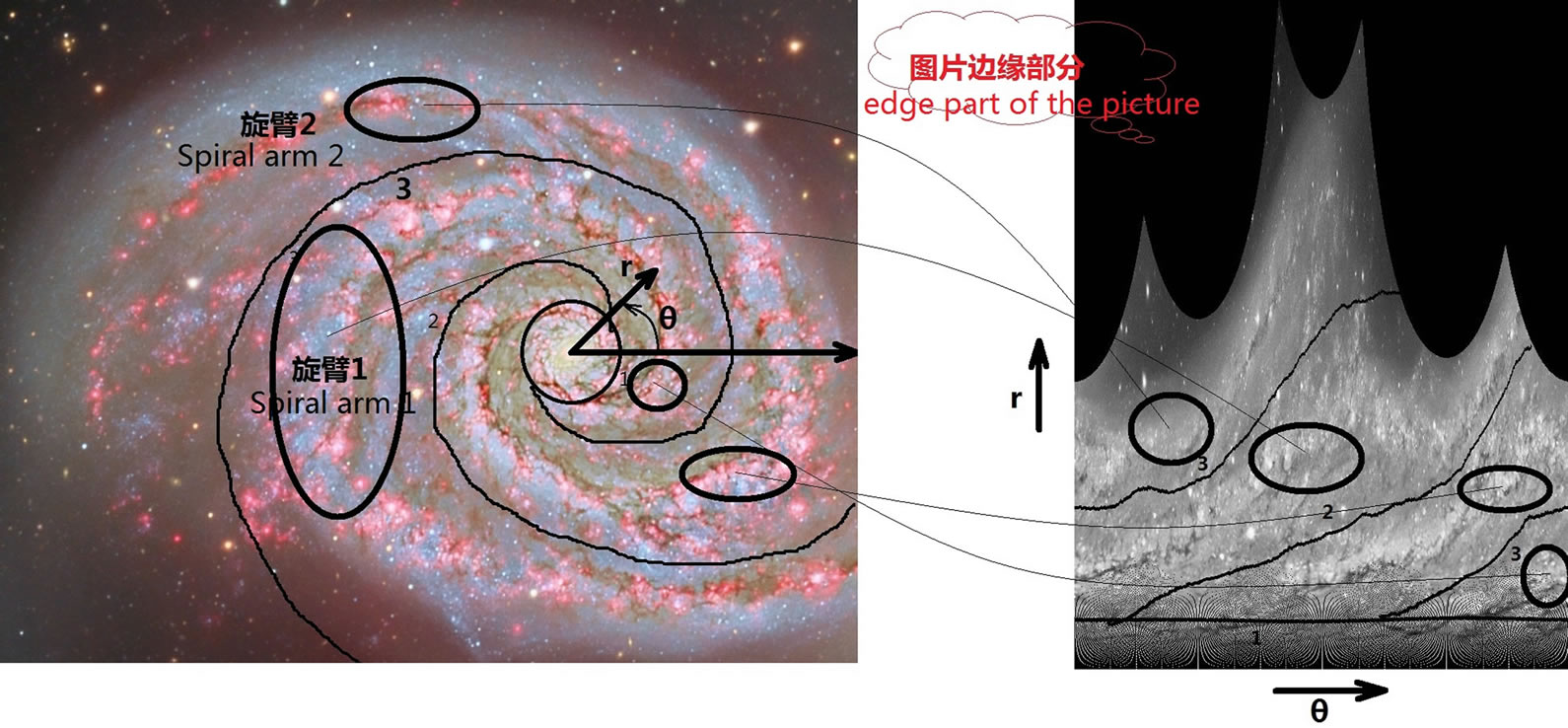
Figure 6. The corresponding relationships between each part in Figures 4 and 5.
relationships between the Figures 4 and 5.
4. Data Processing of one Spiral Arm in the Image of M51 Galaxy
The picture processing in the last step is only a preliminary step for doing the data processing. On that basis, a deeper analysis of Figure 5 must be done.
4.1. Completely Show the Relationship between the Two Spiral Arms of M51
In order to see the interactive relation between the spiral arm 1 and spiral arm 2 more conveniently, it is necessary to join the negative and positive part of q smoothly. We add 2p to all the qs in Figure 5, which means to translate the image (Figure 5) by angle of 2p and then join with the original figure; to indicate the relation, leave a slit between the two pictures. See Figure 7.
Figure 7 exhibits that the two spiral arms of M51 are parallel to each other. Considering that the cause of physical change at the edges is complicated, and removing the edge part, it can also be fund that spiral arms of spiral galaxies are distributed nearly in lines. The exhibittion agrees with the discipline indicated in Formula (1).
4.2. Data Grouping of Spiral Arms
In Figure 5, data of two spiral arms are mixed in the same figure and it is not easy for further data treatment. Thus the data need to be grouped with a computer, which is data grouping. After the data grouping, as shown in Figure 8, process data of positive q-angle of spiral arm 1

Figure 7. Relationship between the two spiral arms of M51. The interval of q axis (horizontal axis) of the angle is expanded from [0, 2p] to [0, 4p] with the unit of 0.01 radian.

Figure 8. Data of positive q-angle of spiral arm 1 of M51. The resolution of the image is 629 ´ 864.
in Figure 5. To minimum the effect of the edge, remove data related to edge effect as shown in Figure 9.
4.3. Linear Regression of Multiple-Valued Function with Weight Coefficient
Use least-square fitting for data in the picture on the right in Figure 9 with Formula (1). It can be found that a q-angle is corresponded with multiple r-values, and the brightness in different r-locations are different. This is a problem of linear regression of multiple-valued function with weight coefficient describing in Mathematical language, but it is omitted as it is outside the category of the physical problem being described in the article and refer to special articles of data analysis regarding this late.
Process the data in the picture on the right in Figure 9 with Formula (1) and algorithm of linear regression of multiple-valued function with weight coefficient and comes Formula (3):
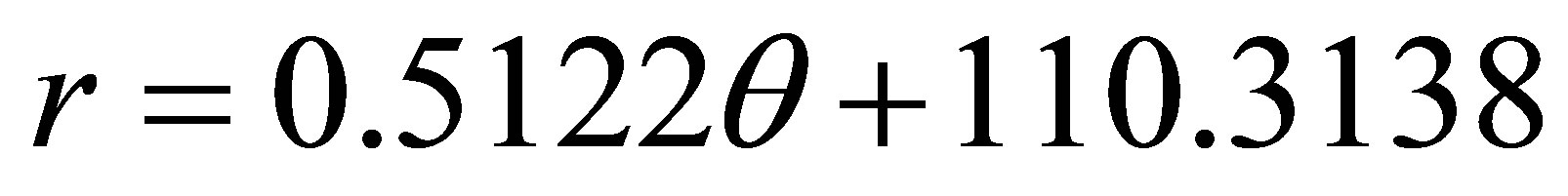 (3)
(3)
Attention: the coefficient in Formula (3) is related to the pixel only in the picture and the units in the formula are not converted into usual units system. The units are: r—pixel, q—0.01 radian The effect after least-square fitting added to Figure 8 is as the line shown in Figure 10.
4.4. Comparison of Track of Movement of Graviton Indicated by Fitting Formula and Original Picture
To verify if the fitting effect is reasonable, compare the track of movement of graviton indicated by fitting Formula (3) to original picture as shown in Figure 11. In Figure 11, the radius r of the circle is 70 pixel units. In addition to showing the galactic center region of galaxy M51, Figure 11 can be used for the comparison of distance in the picture and actual observation distance.

Figure 10. The effect after least-square fitting (refer to the line).

Figure 11. Comparison of track of movement of graviton indicated by fitting formula and original picture. The curve in the picture is fitting curve and the circle with the radius at 70 is the edge of galactic center. Both them can be used to distance scaling.
Figure 11 exhibits that the data fitting agrees the picture well which means that the physical idea Formulas (1) or (2) indicates is correct.
4.5. Fitting Formula of Velocity of Graviton and Rotation Angle of Equivalent Center of Galactic Center of Galaxy M51
Put the distance calibration factor k obtained from Figure 2 in Formula (3) and convert the unit of q into radian, we get the result as Formula (4).
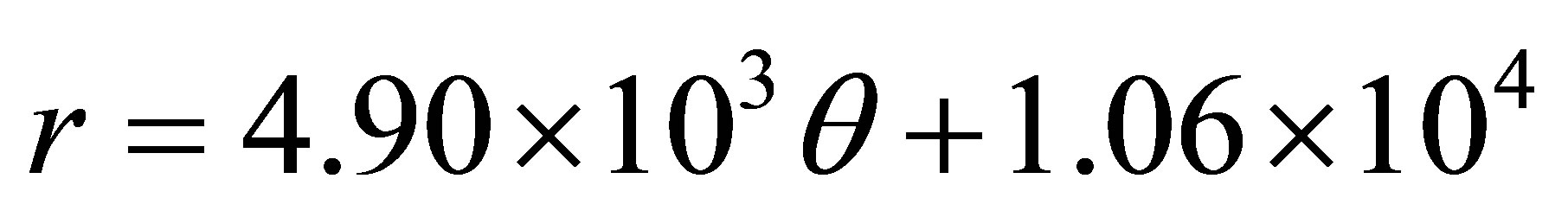 (4)
(4)
Units: r—light year, q—radian.
Comparing Formula (1) and (4), we get the follows:
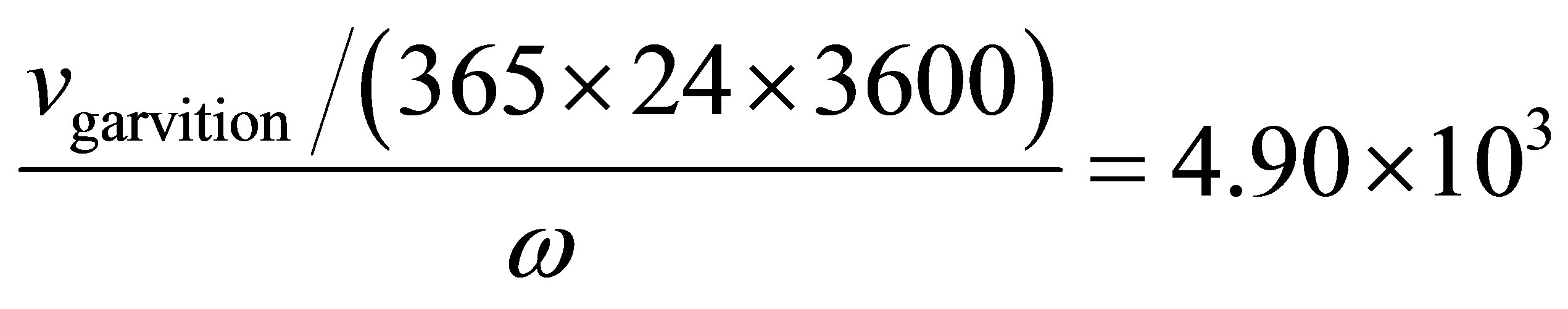 (5)
(5)
 (6)
(6)
Unit:  —Speed of graviton and the unit is c which refers to light velocity.
—Speed of graviton and the unit is c which refers to light velocity.
w—The velocity of rotation angle which plays a main role in spiral galaxies and faster than the velocity of rotation angle of surface of galactic center in spiral galaxies by optical observation. Unit: radian/s.
In current available literature, there is not any record of velocity of rotation angle of equivalent center of spiral galaxies M51, or record of velocity of rotation angle of surface of galactic center of spiral galaxies. As the temperature of galactic center of spiral galaxies is very high while the galactic center is not rigid body, the rotation characterized at the exterior distribution characteristic is formed by the towing effect of gravitational field of interior equivalent center. Thus, the velocity of rotation angle of equivalent center playing a main role is possibly faster than the velocity of rotation angle of surface of galactic center of spiral galaxies by optical observation.
To get the value of , we have to get the value of w. Conversely, the rotation speed of a galaxy could be calculated by using the theory in this article, provided the graviton speed is known for certain.
, we have to get the value of w. Conversely, the rotation speed of a galaxy could be calculated by using the theory in this article, provided the graviton speed is known for certain.
Calculation for an extreme case: as the volume of sun is much smaller than the volume of equivalent center of spiral galaxies M51, it is predictable that the velocity of rotation angle of equivalent center of spiral galaxies M51 is smaller than the velocity of rotation angle of the surface of sun. As known from astronomical materials, the rotation period of solar equator is 25 days.
Namely:

Put it in (6) and we get the upper limit of the velocity of graviton as the follows:
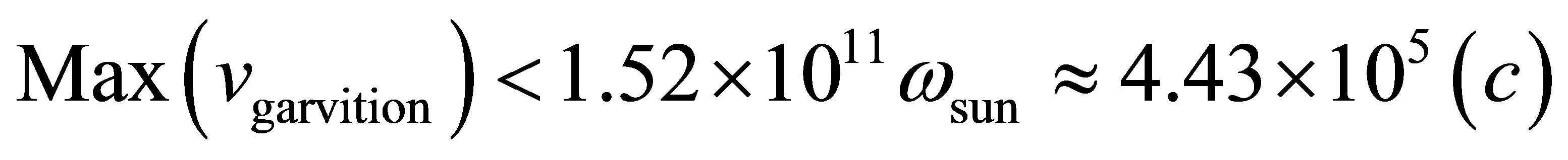
This is to say that maximum velocity of graviton is no larger than 4.43 ´ 105 times of light velocity.
This result is unexpected. But after all, the upper limit of graviton speed has been obtained from observation data.
5. Summary
In sum, we get the follows:
1) The theory of movement track of graviton of spiral galaxies described in Section 2 shows deep physical background of formation of galaxies.
2) Figure 7 exhibits that the two spiral arms of M51 are parallel to each other and spiral arms are distributed nearly in a line which shows that all assumptions about the theory of movement track of graviton of spiral galaxies are correct. Especially, once the graviton is emitted, it moves at a constant velocity.
3) In different spiral galaxies, the velocities of rotation angles of equivalent centers playing main role may be different, but  is a constant. Thus a possible direction of research to fix
is a constant. Thus a possible direction of research to fix  is getting close to the real velocity of graviton through measuring the velocity of rotation angle of equivalent center of galaxies.
is getting close to the real velocity of graviton through measuring the velocity of rotation angle of equivalent center of galaxies.
4) In spiral galaxies, velocity of equivalent center of galaxies affects its formative size together with the mass. It is known from Formula (1) that the size of spiral galaxies is inversely proportional to the velocity of rotation angle of its core. It is also known from the gravity formula, the size of galaxies is proportional to square root of the mass of its equivalent center.
5) Based on the layout of spiral galaxies being perpendicular to the rotation axis, we will get the value of
 with Formula (1). But to get the value of
with Formula (1). But to get the value of
 really, additional separate formula to measure the velocity w of rotation angle of equivalent core is needed. To get the velocity w of equivalent core, another possible direction of research is that trying to use the observed data of the thickness of galactic center of spiral galaxies. The thickness of galactic center of spiral galaxies is presented as a certain function of the velocity of rotation angle of its core. Of course further research work is needed to get such relationship expression.
really, additional separate formula to measure the velocity w of rotation angle of equivalent core is needed. To get the velocity w of equivalent core, another possible direction of research is that trying to use the observed data of the thickness of galactic center of spiral galaxies. The thickness of galactic center of spiral galaxies is presented as a certain function of the velocity of rotation angle of its core. Of course further research work is needed to get such relationship expression.
6) That the theory of movement track of graviton coincides with distribution chart of spiral arms of galaxies M51 verified the assumption of the theory is correct. Especially the velocity of movement of graviton is a constant is now supported with experimental data. The characteristic (refer to aforementioned assumption 1 and 2) of the theory is coincident with Archimedes’ spiral in mathematics [7].
7) The characteristic of the theory of movement track of graviton (refer to aforementioned assumption 1 and 2) is in keeping with the description in literature [8], namely that the distribution characteristic of velocity of stars’ movement in spiral arms along with the radius r is coincident with Lagrange velocity distribution. It shows that the theory of movement track of graviton is compatible with the popular kinetic theory in astronomy, but theory of movement track of graviton shows further physical characteristic.
6. Acknowledgements
Great thanks to Maths professor Doctor Li Jinming in China Agricultural University for providing great support and astronomical export Professor Cao Shenglin in Beijing Normal University for offering plenty of valuable suggestions in the research of the project.
REFERENCES
- T. Adam, N. Agafonova, et al., “Measurement of the Neutrino Velocity with the OPERA Detector in the CNGS Beam,” 2011. http://arxiv.org/abs/1109.4897
- G. Brumfiel, “Particles Break Light-Speed Limit,” 2011. http://www.nature.com/news/2011/110922/full/news.2011.554.html
- “The Scientists Affirm that Speed of Neutrino Isn’t Supervelocity of Light and still Submits to the Einstein’s Theory,” 2012. http://tech.sina.com.cn/d/2012-06-13/09067262117.shtml
- M. Min and K. Xu, Progress in Astronomy, Vol. 25, 2007.
- Z. Chen and P. Williams, Progress in Astronomy, Vol. 24, 2006.
- P. A. Luo, Journal of Modern Physics, Vol. 3, 2012.
- Y. H. Shen, Z. Z. Liang, et al., “Practical Mathematical Manual,” Science Press, 2001, p. 79.
- T.-F. Chen, G. H. Vatistas, et al., Journal of Thermal Science, Vol. 17, 2008, pp. 61-63. http://dx.doi.org/10.1007/s11630-008-0061-6



