Journal of Modern Physics
Vol.5 No.1(2014), Article ID:42261,7 pages DOI:10.4236/jmp.2014.51010
MHD Flow of a Non-Newtonian Power Law through a Conical Bearing in a Porous Medium
1Department of Mathematics, Faculty of Science, Benha University, Benha, Egypt
2Department of Mathematics, Faculty of Science, Princess Norah Bint Abdelrahman University, Riyadh, KSA
Email: gamalm60@yahoo.com
Received October 10, 2013; revised November 12, 2013; accepted December 11, 2013
ABSTRACT
The problem of analytical study of the MHD effect through a porous medium of the non-isothermal flow of a non-Newtonian power law lubricant through the gap of conical bearing through a porous medium when an external magnetic field is applied. At first, the more general basic equations of motion, continuity and energy in curvilinear form in the width direction are derived. Then, as a special case, a conical bearing gap is considered. By integrating a modified form of Reynolds equation, the bearing characteristics for a non-Newtonian power law lubricant when an external magnetic field is applied through a porous medium are obtained. Numerical results were presented in each of these forms: pressure, temperature and capacity of the conical bearing. The effects of the parameters of the non-Newtonian power law, magnetic field and porous medium are shown and discussed.
Keywords:MHD; Non-Newtonian Fluid; Conical Bearing; Porous Medium
1. Introduction
Firstly the study of an electrically conducting fluid through a porous medium under the influence of a magnetic field has many applications in engineering problems such as magnetohydrodynamics (MHD) generators, liquid metal, plasma studies, nuclear reactors, metal working process, geothermal energy extraction and in many other applications. MHD flow of non-Newtonian fluids also has application in different fields. An important field is the electromagnetic propulsion. And some fluids with thixotropic behavior help in the flow of blood, coating of paper, plastic extension and lubrication with heavy oils and greases.
Advance in modern technology and extremely severe requirements for rotating elements of machines imposes upon design engineers the necessity of continous development of improved lubricants in order to assure the stability, safe operation and reliability of various bearings. For operations under high molecular-weight polymer components are used in modern bearings. Such lubricants exhibit a non-Newtonian Rheological behavior [1].
The effect of the non-Newtonian behaviour of lubricants on the performance of hydrodynamic cylindrical journal bearing of infinite width has been investigated by I. Teipel et al. [2,3], and K. wierzcholski [4]. A somewhat similar problem but for cylindrical bearing of finite width had been considered. Swamy et al. [5].
This problem was studied in the magnetic case by Z. Nowak et al. [1], and also had been studied in magnetic field and a Newtonian lubricant by R. Janiszweski [6]. Very recently, Abdel-Rahman G. M. [7] studied the above mention flow of a non-Newtioan power law through a conical bearing in an applied magnetic field in the absence of the porous medium ( ).
).
In the present paper a magnetohydrodynamic flow for a non-Newtonian power law lubricant through the gap of a conical journal bearing in a porous medium is investigated. At first, the more general basic equations of motion, continuity and energy in curvilinear form in the width direction are derived. Then, as a special case, a conical bearing gap is considered. By integrating a modified form of Reynolds equation the bearing characteristics for a non-Newtonian power law lubricant when an external magnetic field is applied through a porous medium are obtained. It seems to the author that they succeeded in omitting the numerical procedures and obtained a relatively solution to the problem discussed.
2. Mathematical Analysis
The analytical study of the MHD effect through a porous medium of the non-isothermal flow of a non-Newtonian power law lubricant through the gap of conical bearing when an external magnetic field through the curvilinear bearing gap will be performed by using the following basic equations in orthogonal curvilinear coordinates.
Equation of motion:
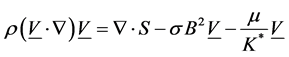 (1)
(1)
Equation of continuity:
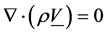 (2)
(2)
Equation of energy:
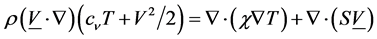 (3)
(3)
where 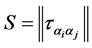 -is the stress tensor in the lubricant,
-is the stress tensor in the lubricant, ![]() is the local lubricant velocity vector,
is the local lubricant velocity vector, ![]() is the dynamic viscosity,
is the dynamic viscosity, ![]() is the lubricant mass density
is the lubricant mass density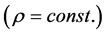 ,
, 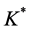 is the permeability of the porous medium,
is the permeability of the porous medium, ![]() is the specific heat of the lubricant,
is the specific heat of the lubricant, ![]() is the temperature in the lubricant,
is the temperature in the lubricant, ![]() is its coefficient of thermal conductivity,
is its coefficient of thermal conductivity, ![]() is the electric conductivity in the lubricant and
is the electric conductivity in the lubricant and ![]() is the applied magnetic field.
is the applied magnetic field.
The movable local coordinate system —connected with the rotating journal surface—is assumed to be curvilinear and orthogonal. The components of the stress tensor S are expressed as
—connected with the rotating journal surface—is assumed to be curvilinear and orthogonal. The components of the stress tensor S are expressed as 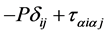 where
where  is the hydrodynamic pressure and
is the hydrodynamic pressure and  is the Kronecker symbol.
is the Kronecker symbol.
From the Reiner-Rivlin equations follows immediately that for a power law lubricant, as considered is this paper, the stress-strain relations are of the form:
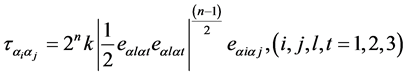 (4)
(4)
where k is the fluid of consistency and n is the flow behaviour index of the lubricant.
The components of the strain tensor 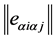 are:
are:
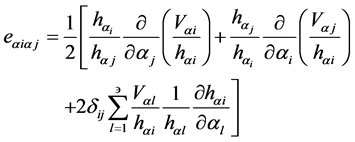 (5)
(5)
where 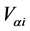 denote the components of velocity vector in
denote the components of velocity vector in 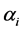 -direction respectively.
-direction respectively.
In the first approximation, both the fluid of consistency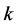 , and the flow behaviour index
, and the flow behaviour index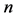 , are assumed to be independent of temperature. The viscous dissipation (dissipation function) for the lubricant, however, taken into account. Since the journal of the bearing always is a rotating body, the lame’s coefficients
, are assumed to be independent of temperature. The viscous dissipation (dissipation function) for the lubricant, however, taken into account. Since the journal of the bearing always is a rotating body, the lame’s coefficients  become respectively
become respectively![]() . Assuming the ratio of the radial component of 1ubricant velocity to the peripheral velocity of the journal bearing to be of order of the relative radial clearance and hence, neglecting the terms having the order of the latter, than equations of: motion, continuity and energy, become
. Assuming the ratio of the radial component of 1ubricant velocity to the peripheral velocity of the journal bearing to be of order of the relative radial clearance and hence, neglecting the terms having the order of the latter, than equations of: motion, continuity and energy, become
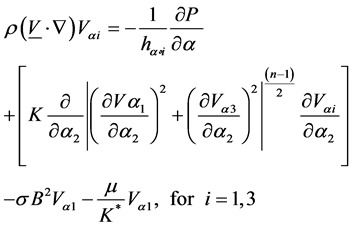 (6)
(6)
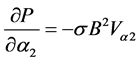 (7)
(7)
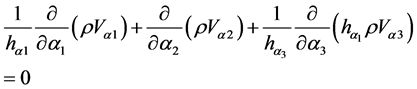 (8)
(8)
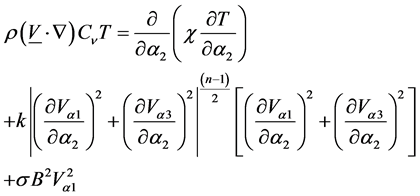 (9)
(9)
For 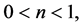 Equations (6)-(9) describe the magneto-hydrodynamic flow of a non-Newtonian power law lubricant in a porous medium through the curvilinear (in width direction) gap of a slide bearing.
Equations (6)-(9) describe the magneto-hydrodynamic flow of a non-Newtonian power law lubricant in a porous medium through the curvilinear (in width direction) gap of a slide bearing.
For n = 1, the equations listed above hold for a Newtonian gap flow [6], the unknown functions , p and T may be found by solving the Equations (6)-(9).
, p and T may be found by solving the Equations (6)-(9).
In the special case of a conical bearing gap , the curvilinear coordinates  become
become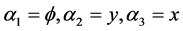 , respectively, see Figure 1.
, respectively, see Figure 1.
Thus, the Lame’s coefficients are ![]()
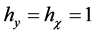 where
where 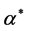 denotes the slope of the generating line of conical surface. The components of the local lubricant velocity
denotes the slope of the generating line of conical surface. The components of the local lubricant velocity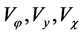 , the hydrodynamic pressure
, the hydrodynamic pressure 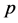 and temperature
and temperature ![]() are now assumed to be of the following forms:
are now assumed to be of the following forms:
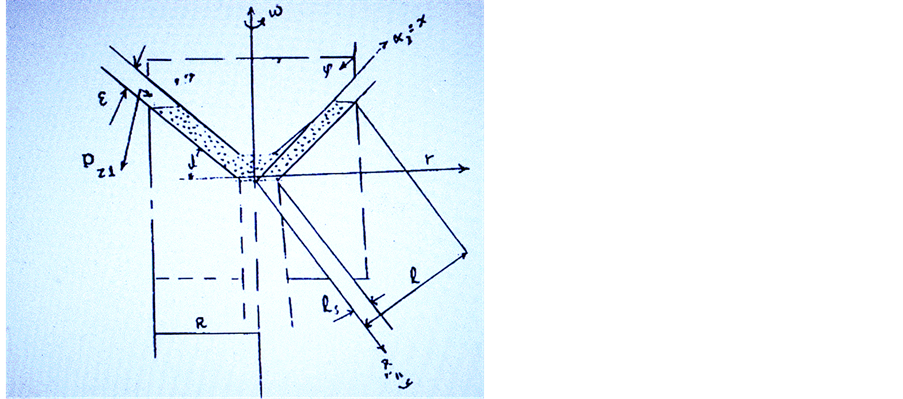
Figure 1. Conical bearing gap.
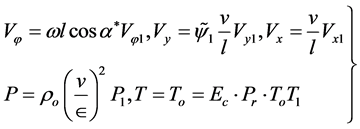 (10)
(10)
where  and
and 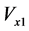 are the dimensionless components of the local lubricant velocity in the
are the dimensionless components of the local lubricant velocity in the 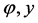 and
and  directions, respectively,
directions, respectively, ![]() is the dimensionless hydrodynamic pressure
is the dimensionless hydrodynamic pressure 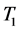 is the temperature,
is the temperature,  is the length of the cone generating line, e denotes the height of the gap,
is the length of the cone generating line, e denotes the height of the gap, 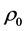 is the dimensional characteristic value of lubricant density,
is the dimensional characteristic value of lubricant density, ![]() denotes the ambient temperature, w is the angular velocity of the journal, Ec and Pr are the Eckert and Prandtl numbers, respectively. Moreover
denotes the ambient temperature, w is the angular velocity of the journal, Ec and Pr are the Eckert and Prandtl numbers, respectively. Moreover
 (11)
(11)
where ![]() is the modified Kinematic viscoity,
is the modified Kinematic viscoity, ![]() is a dimensionless number that characterizes the magnetic field,
is a dimensionless number that characterizes the magnetic field,
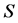 is a dimensionless porous medium and
is a dimensionless porous medium and 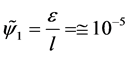
is the relative redial clearance of the bearing.
Let 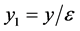 be the dimensionless vertical coordinate, and
be the dimensionless vertical coordinate, and 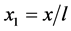 be the dimensionless coordinate in the direction of cone generating line.
be the dimensionless coordinate in the direction of cone generating line.
After substituting Equations (10) and (11) into Equations (6)-(9), provided that the axisymmetrical flow is considered, with simultaneous neglecting the terms of the  -order, one obtains finally:
-order, one obtains finally:
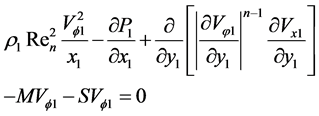 (12)
(12)
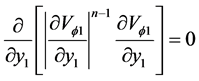 (13)
(13)
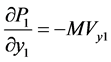 (14)
(14)
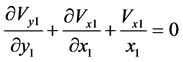 (15)
(15)
 (16)
(16)
for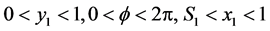 , where
, where  and
and 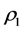 are the dimensionless thermal conductivity and density of the lubricant, respectively,
are the dimensionless thermal conductivity and density of the lubricant, respectively, 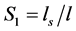 is the dimensionless distance between the sleeve surface and the axis of the journal. Moreover,
is the dimensionless distance between the sleeve surface and the axis of the journal. Moreover, 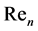 signifies the modified Reyolds number, defined by
signifies the modified Reyolds number, defined by
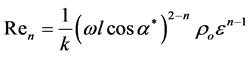 (17)
(17)
The term  appearing Equation (12) describes the centrifugal forces generated in the lubricant by the rotation of the journal. The expression
appearing Equation (12) describes the centrifugal forces generated in the lubricant by the rotation of the journal. The expression 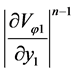 occurring in Equations (12), (13) and (16) determines the dimensionless apparent viscosity of the lubricant. The remaining “viscous” terms in (12), (13) and (16) have been neglected since their values are of the
occurring in Equations (12), (13) and (16) determines the dimensionless apparent viscosity of the lubricant. The remaining “viscous” terms in (12), (13) and (16) have been neglected since their values are of the 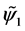 -order. Equation (13) does not appear the term,
-order. Equation (13) does not appear the term, 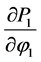 , because of the
, because of the
per-assumed axisymmetry of the lubricant flow.
Form the simplified form of Equation (14) follows immediately that the pressure has been assumed to be uniform along the film thickness.
In the equation of energy (16) the terms due to the forced heat convection in the lubricant have been disregarded, since their values are of the  -order. However, it should be noted here that the terms due both to the viscous dissipation and heat conduction in the radial direction have been taken onto account.
-order. However, it should be noted here that the terms due both to the viscous dissipation and heat conduction in the radial direction have been taken onto account.
3. Solution of Equations
Assuming the lubricant to be an incompressible flow, we have 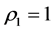 since the difference between the ambient temperature and the temperature both in the gap and in the bearing sleeve, is generally small, the coefficient of thermal conductivity is assumed to be independent of temperature i.e.
since the difference between the ambient temperature and the temperature both in the gap and in the bearing sleeve, is generally small, the coefficient of thermal conductivity is assumed to be independent of temperature i.e. 
The boundary conditions to this system are
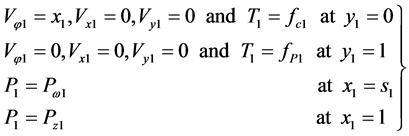 (18)
(18)
where 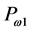 is the dimensionless pressure,
is the dimensionless pressure,  is the ambient pressure fc1 is the dimensionless temperature on the journal surface and
is the ambient pressure fc1 is the dimensionless temperature on the journal surface and  is the dimensionless temperature of the bearing sleeve.
is the dimensionless temperature of the bearing sleeve.
For Equation (13) solution for 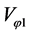 which satisfy the boundary condition (18) is
which satisfy the boundary condition (18) is
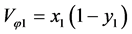 (19)
(19)
After substituting the function  into Equation (12) and taking into account the boundary condition (18), we find
into Equation (12) and taking into account the boundary condition (18), we find 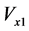 as a function of the parameter
as a function of the parameter![]() , we get
, we get
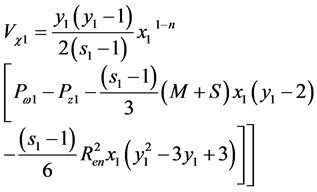 (20)
(20)
substituting the function  into Equation (15), hence, we get
into Equation (15), hence, we get
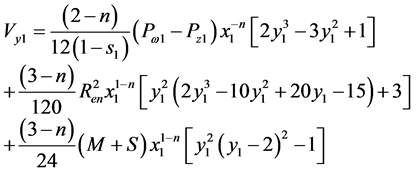 (21)
(21)
The boundary condition  at
at  imposed upon the velocity component
imposed upon the velocity component 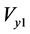 leads to an equation from which the pressure function may be determined. After solving this equation with the boundary condition (18), we obtain the sought-for function
leads to an equation from which the pressure function may be determined. After solving this equation with the boundary condition (18), we obtain the sought-for function  as
as
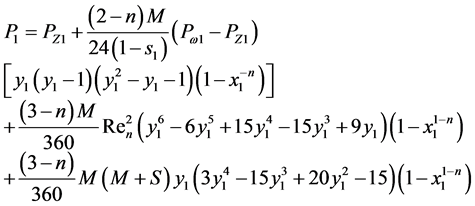
(22)
By inserting the function 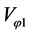 into Equation (16) and integrating it with boundary condition (18), we calculate the temperature function
into Equation (16) and integrating it with boundary condition (18), we calculate the temperature function 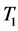 as
as
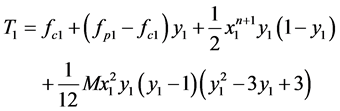
 (23)
(23)
For 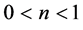 the above relations hold for a nonNewtonian power law lubricant with time independent rheological properties, the apparent viscosity of which decrease with increasing shear rate for constant magnetic field.
the above relations hold for a nonNewtonian power law lubricant with time independent rheological properties, the apparent viscosity of which decrease with increasing shear rate for constant magnetic field.
4. Numerical Discussion and Conclusions
Numerical values for the pressure and temperature distributions from Equations (22) and (23) for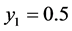 ,
, 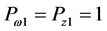 and
and 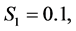
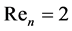 in Figures 2-4 for
in Figures 2-4 for
 (a)
(a)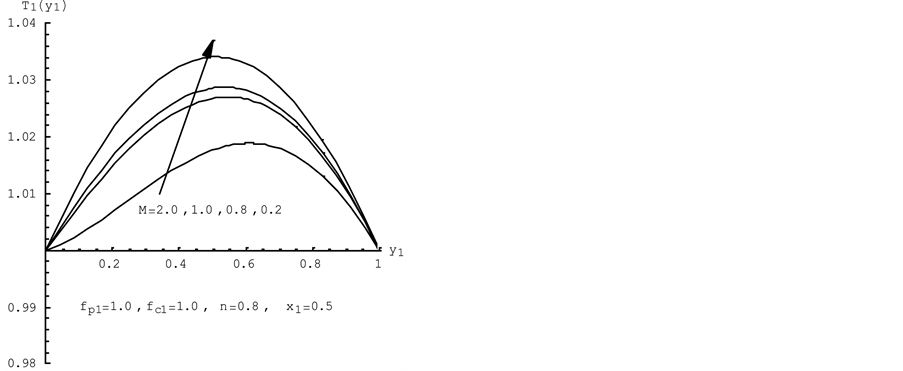 (b)
(b)
Figure 2. Effect of magnetic parameter on (a) the dimensionless pressure profile and (b) the dimensionless temperature profile.
 (a)
(a)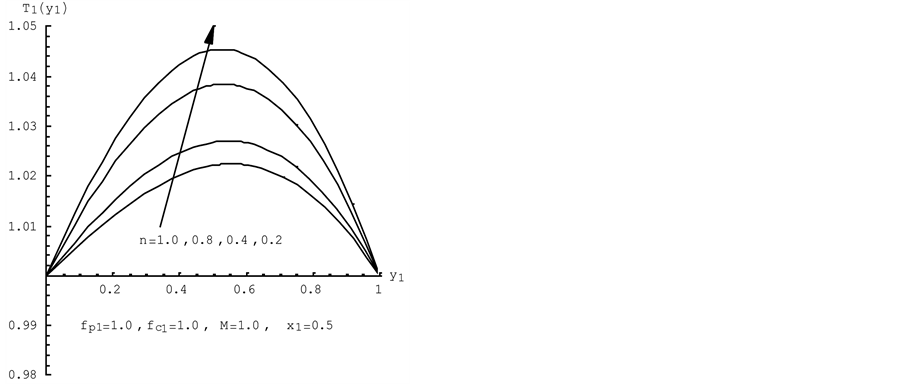 (b)
(b)
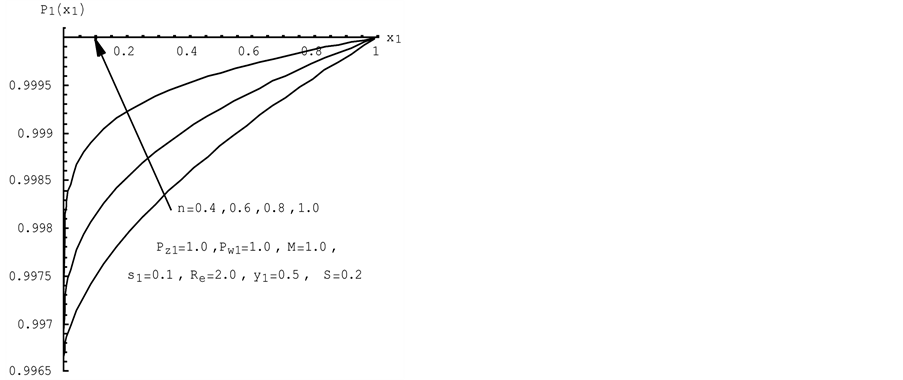
Figure 3. Effect of a non-Newtonian power law lubricant parameter on (a) the dimensionless pressure profile and (b) the dimensionless temperature profile.
some values of the magnetic parameter  the parameter of the non-Newtonian power law lubricant
the parameter of the non-Newtonian power law lubricant 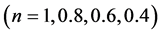 and the parameter of the porous medium
and the parameter of the porous medium  from these results we can state the following:
from these results we can state the following:
Figures 2(a) and (b) display the dimensionless pressure and the dimensionless temperature profiles under the different the magnetic parameter. The pressure and the temperature profiles decrease with increasing the magnetic parameter.
Figures 3(a) and (b), it is clear that the pressure increases with the increase of the non-Newtonian power law lubricant parameter  in comparison to the respective pressure values due to a Newtonian flow
in comparison to the respective pressure values due to a Newtonian flow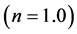 . These decreases are caused by a decreasing apparent viscosity of the non-Newtonian lubricant as compared to the dynamic viscosity of a Newtonian flow,
. These decreases are caused by a decreasing apparent viscosity of the non-Newtonian lubricant as compared to the dynamic viscosity of a Newtonian flow,
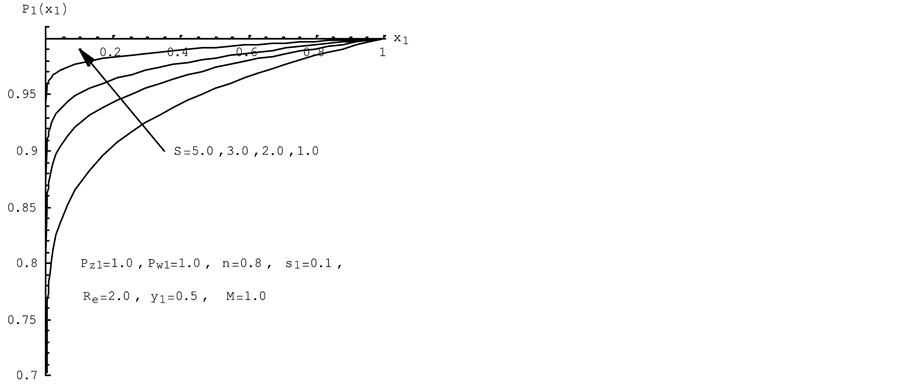
Figure 4. Effect of a porous medium parameter on the dimensionless pressure profile.
and the decreases of the temperature for a non-Newtonian lubricant are distinctly greater than those corresponding to the Newtonian flow. These decreases are due to viscous dissipation arising in the lubricant. The phenomenen discussed may be explained by the fact that for the non-Newtonian lubricant greater values of internal friction forces are generated than for a Newtonian flow. The latter produce, in turn, greater heat quantities during the motion of particles.
Figure 4 displays the dimensionless pressure profile under the different the porous medium parameter. The pressure profile decreases with increasing the porous medium parameter.
The capacity 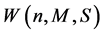 of the conical bearing can be expressed in the following dimensionless from:
of the conical bearing can be expressed in the following dimensionless from:
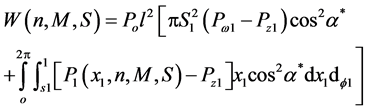 (24)
(24)
substituting the function ![]() into Equation (22), hence, we get
into Equation (22), hence, we get
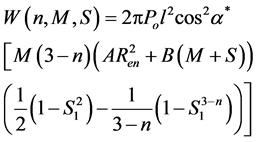 (25)
(25)
where
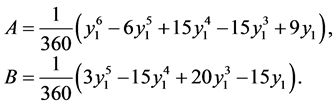
where  is the characteristic pressure value. Provided that
is the characteristic pressure value. Provided that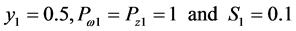 .
.
In Figures 5(a) and (b), it is clear that the capacity 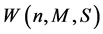 increases with the increase of the nonNewtonian power law lubricant parameter
increases with the increase of the nonNewtonian power law lubricant parameter , while the increases of the capacity
, while the increases of the capacity 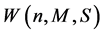 for the porous medium parameter
for the porous medium parameter ![]() decreasing.
decreasing.
Figures 6(a) and (b), the capacity 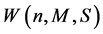 increases with the increase of each of the magnetic parameter
increases with the increase of each of the magnetic parameter 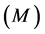 and the porous medium parameter
and the porous medium parameter![]() .
.
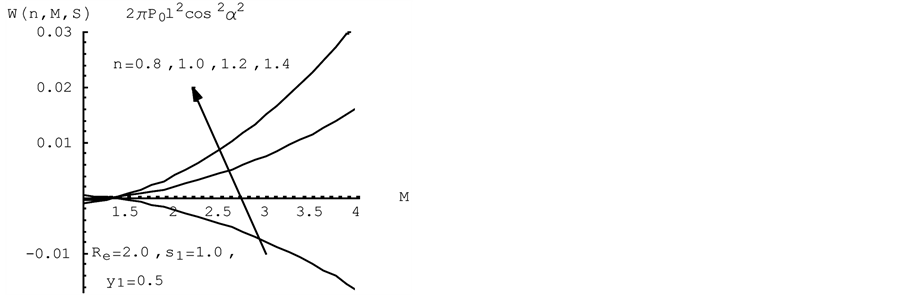
And in Figures 7(a) and (b), it is clear that the capacity 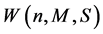 increases with the decrease of the the magnetic parameter
increases with the decrease of the the magnetic parameter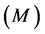 , while the increases of the capacity
, while the increases of the capacity  for the non-Newtonian power law lubricant parameter
for the non-Newtonian power law lubricant parameter 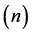 increasing.
increasing.
 (a)
(a) (b)
(b)
Figure 5. (a) The capacity 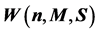 for various
for various 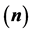 and (b) The capacity
and (b) The capacity 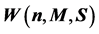 for various
for various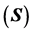 .
.
 (a)
(a)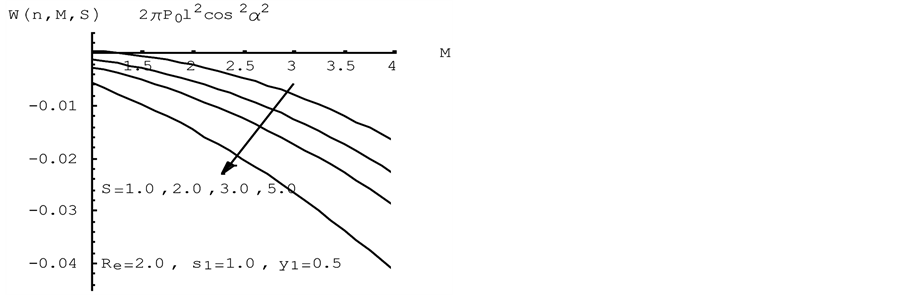 (b)
(b)
Figure 6. (a) The capacity  for various
for various  and (b) The capacity
and (b) The capacity  for various
for various .
.
 (a)
(a) (b)
(b)
Figure 7. (a) The capacity  for various
for various  and (b) The capacity
and (b) The capacity  for various
for various .
.
REFERENCES
- Z. Nowak and K. Wierzcholski, Acta Mechanica, Vol. 50, 1984, pp. 221-230. http://dx.doi.org/10.1007/BF01170962
- J. Teipel and A. Waterstraat, Knostruktion, Vol. 32, 1980, pp. 373-378.
- I. Teipel, Ingenieur-Archiv, Vol. 49, 1980, pp. 137-144.
- K. Wierzcholski, Rev Rom. Sci. Tech. Mech. App., Vol. 25, 1980, pp. 319-339.
- S. T. N. Swamy, B. S. Prabhu and B. V. A. Rao, Wear, Vol. 31, 1975, pp. 277-285. http://dx.doi.org/10.1016/0043-1648(75)90162-3
- R. Janiszewski, Zagadnienia Eksploatacji Maszya, Vol. 37, 1979, pp. 17-24.
- G. M. Abdel-Rahman, Applied Mathematics and Computation, Vol. 159, 2004, pp. 237-246. http://dx.doi.org/10.1016/j.amc.2003.11.041

