Journal of Modern Physics
Vol.05 No.15(2014), Article ID:50144,9 pages
10.4236/jmp.2014.515149
Non-Classical Formulation of Photon Energy for the Degenerate Parametric Oscillator
Solomon G. Belete
Physics Department, Jimma University, Jimma, Ethiopia
Email: solgett@yahoo.com, solgett@gmail.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 18 June 2014; revised 15 July 2014; accepted 9 August 2014
ABSTRACT
We have analyzed photon statistics and quadrature squeezing of the signal mode produced by one-mode subharmonic generator. It is found that the mean photon energy of the signal mode is twice of a twin signal light beam. And the energy fluctuations of the two signal light beams are four times that of one of the signal light beams. We have also shown that the photon energy quadrature squeezing of the output signal mode is exactly equal to that of the cavity signal mode. In light of this, the global quadrature squeezing of the signal mode is independent of the mean photon energy. On the basis of the above results, the quantum analysis of a one-mode sub-harmonic generating system should somehow be modified.
Keywords:
Signal Mode, A Twin Signal Light Beam, Photon Energy, Energy Fluctuations, Energy Quadrature Squeezing

1. Introduction
A one-mode sub-harmonic generator is one of the most interesting and well-studied quantum optical systems. This system consists of a nonlinear crystal which is pumped by coherent light and placed inside a cavity coupled to a vacuum reservoir. This quantum optical process leads to the generation of squeezed light. A theoretical analysis of the quadrature squeezing and photon statistics of a signal mode produced by a one-mode sub-har- monic generator has been made by a number of authors [1] -[9] . It has been established that the signal mode has a maximum of 50% squeezing below the coherent-state level [1] -[4] .
In a one-mode sub-harmonic generator, a pump photon of frequency 2ω is down converted into a pair of signal photons each of frequency (ω). It is to be recalled that the Hamiltonian describing the process of sub-har- monic generation consists of the operators 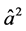 and
and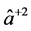 . And the quantum analysis of the signal mode is usually carried out employing the operator’s
. And the quantum analysis of the signal mode is usually carried out employing the operator’s 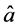 and
and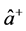 . However, such analysis leads, among others, to one- half of the mean photon number of the signal mode [2] [4] -[8] [10] -[14] . This is surely the mean number of one set of the signal photons (a twin signal light beam), consisting of one photon from each pair [1] . Since the other set of the signal photons is not included in such analysis, we seek to resolve this problem by superposing the Q function of the two set of signal photons (the signal mode), each set consisting of one photon from each pair. The resulting Q function is used to determine the mean photon number, the mean energy, the variance of the photon number, the energy fluctuations, the photon number quadrature variance, the photon energy quadrature fluctuations, the photon number quadrature squeezing and the photon energy quadrature squeezing of the two signal light beams.
. However, such analysis leads, among others, to one- half of the mean photon number of the signal mode [2] [4] -[8] [10] -[14] . This is surely the mean number of one set of the signal photons (a twin signal light beam), consisting of one photon from each pair [1] . Since the other set of the signal photons is not included in such analysis, we seek to resolve this problem by superposing the Q function of the two set of signal photons (the signal mode), each set consisting of one photon from each pair. The resulting Q function is used to determine the mean photon number, the mean energy, the variance of the photon number, the energy fluctuations, the photon number quadrature variance, the photon energy quadrature fluctuations, the photon number quadrature squeezing and the photon energy quadrature squeezing of the two signal light beams.
2. The Q Function
We seek first to determine the Q function for the signal mode produced by one-mode sub-harmonic generator. This can be done by superposing the Q functions of the two sets of signal photons, each set consisting of one signal photon from each pair.
We recall that the Q function for the signal light beam has the form [1]
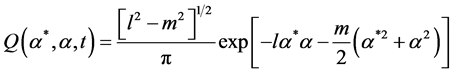 , (1)
, (1)
where
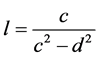 , (2)
, (2)
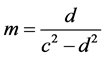 , (3)
, (3)
with
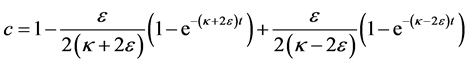 , (4)
, (4)
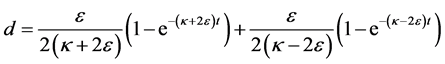 . (5)
. (5)
Here, 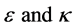 are the amplitude of the driving coherent light and the cavity damping constant, respectively.
are the amplitude of the driving coherent light and the cavity damping constant, respectively.
We now proceed to determine the Q function for the two signal light beams produced by one-mode sub-har- monic generators. The Q function for the superposition of two light beams can be defined by [1]
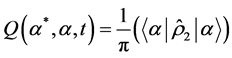 , (6)
, (6)
is the c-number corresponding to normally ordered density operator divided by . Suppose
. Suppose 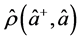 is density operator for a certain light beam. Then upon expanding the density operator in normal order
is density operator for a certain light beam. Then upon expanding the density operator in normal order
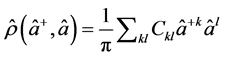 . (7)
. (7)
And employing the completeness relation for coherent state
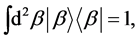 (8)
(8)
one can easily find
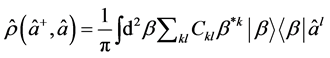 (9)
(9)
and using the identity

there follows

This expression can be put in terms of the displacement operator in the form

We now realize that the density operator for the superposition of the first light beam and another one expressible as [1]

so that in view of (12), we have

in which

and

Now the combination of (6) and (14) give rise the Q function for superposition of two light beams as in the form

Finally, applying the binomial theorem, one can readily establish the Q function for a pair of superposed cavity light beams as [1]

where

and

With the aid of Equation (1), the Q function for one of the signal light beam can be put in the form

And the Q function for the other signal light beam can be written as

Now introducing (21) and (22) into (18), we have

Thus upon carrying out the integration over 


we readily obtain

where

and

One can easily check that the Q function for the two signal light beams given by Equation (25) is normalized to unity.
3. Photon Statistics
In this section, we seek to study the statistical properties of the two signal light beams produced by the one- mode sub-harmonic generators.
3.1. The Mean Energy
Here, we wish to calculate the mean photon number and the mean photon energy of the two signal light beams. The mean photon number, for the cavity light, is defined by

Then the mean photon number can be written in terms of the Q function as

On account of Equation (25), expression (29) can be put in the form

so that upon carrying out the integration, employing the relation given by (24), and performing the differentiation with respect to a and applying the condition a = 0, we readily get

Now in view of (26) and (27) along with (2) and (3), we easily find

so that on account of (4), we have

Hence at steady state, we see that

This is the mean photon number of the two signal light beams which is twice of the mean photon number obtained in Ref. [2] -[8] .
On the other hand, for normally ordered operators and a cavity mode coupled to a vacuum reservoir, the output and cavity operators can be related by [1]

Then combining (28) and (35), we have

This indicates that the mean photon number of the output light is 
Moreover, we note that the quantum Hamiltonian of a single-mode light has the form [1]

where

and

so that the mean photon energy of the two signal light beams can be put as

in which 


where 
3.2. The Energy Fluctuations
We next proceed to obtain the variance of the photon number and the energy fluctuations for the two signal light beams produced by the one-mode sub-harmonic generator. The variance of the photon number, for the cavity light, is defined by

Using the commutation relation

which holds true for a pair of superposed light beams, we find

Thus with the aid of Equation (25), the expectation value of 

so that upon carrying out the integration, employing the relation given by (24), and performing the differentiation with respect to a and applying the condition a = 0, we readily obtain

Therefore, in view of (2) and (3), there follows

Now combination of (32), (44), and (47) yields

Then with the aid of Equations (4) and (5), we obtain

which at steady-state turns out to be

This is the variance of the photon number for the two signal light beams. This variance is four times the variance of the photon number obtained in Ref. [1] -[8] .
On the other hand, substitution of (35) into Equation (44) results in

in which

This shows that the variance of the photon number of the output light is 
Furthermore, the energy fluctuations for the cavity mode, is defined by

then, using the commutation relation

and combination of (44) and (53) along with (38) and (39) results in

This shows that the energy fluctuation is equal to the product of the square of photon energy and the photon number fluctuation.
4. Quadrature Squeezing
We wish here to study the squeezing properties of the two signal light beams produced by one-mode sub- harmonic generator. We define the photon number quadrature variance for a pair of superposed cavity light beams by

where

and

are the plus and minus photon number quadrature operators for the cavity light. The first term on the right hand side of Equation (56) represents the photon number quadrature variance for a pair of superposed coherent light beams. It is also the commutation relation for the photon number annihilation and creation operators repre- senting the superposed light beams. Now employing the Q function described by Equation (25), one can easily verify that

On account of (57), (58), and (59), Equation (56) can be put in the form

Then using Equation (25), the expectation value of 

so that upon carrying out the integration, applying the relation given by (24), and performing the differentiation with respect to a and introducing the condition a = 0, we readily find

Hence in view of (26), (27) along with (2), (3), and (5), there follows

With the aid of (33), (60), and (63), we easily get

This is the photon number quadrature variance of the two signal light beams which is twice of the quadrature variance obtained in Ref. [1] -[8] . In addition we observe that the signal mode is in a squeezed state and the squeezing occurs in the plus quadrature. Moreover, applying (35) in Equation (60), we get

in which

We observe that the photon number quadrature variance of the output light is κ times that of the cavity light.
On the other hand, photon-energy quadrature variance for the cavity light is defined by

where

and

are the plus and minus photon-energy quadrature operators for the cavity light. The first term on the right hand side of Equation (67) represents the photon energy quadrature variance for a pair of superposed coherent light beams. It is also the commutation relation for the photon energy annihilation and creation operators representing the superposed light beams.
Then employing (54), (60), (64), (68), and (69) along with (38) and (39), we put Equation (67) in the form

in which 2ħω being photon-energy quadrature variance of a pair of superposed coherent light beams. This equation can be rewritten, at steady state, as

Hence by comparing Equations (64) and (71), we observe that the photon-energy quadrature variance is equal to the product of the photon energy and the photon number quadrature variance.
Next we seek to obtain the quadrature squeezing of the two signal light beams relative to the quadrature variance of a pair of superposed coherent light beams. We thus define the photon number quadrature squeezing of the cavity signal mode by [1]

so that on account of (64), there follows

Moreover, at steady-state and at threshold, the photon number quadrature squeezing turns out to be

We note that at steady state and at threshold there is a 50% squeezing of the signal mode below the cavity coherent-state level.
On the other hand, we define the photon number quadrature squeezing of the output signal mode by [1]

where 

This indicates that the photon number quadrature squeezing of the output signal mode is exactly equal to that of the cavity signal mode.
Furthermore, we can also define photon-energy quadrature squeezing the cavity signal mode by

Thus in view of (70) and (77), we have

which indicates that photon-energy quadrature squeezing is the same as that of the photon number quadrature squeezing.
5. Conclusions
In this paper, we studied photon statistics and quadrature squeezing of the two signal light beams produced by one-mode sub-harmonic generator. So far we know that the Hamiltonian describing the process of sub-harmonic generation consists of the operators’ a2 and a+2. And the quantum analysis of the signal mode is usually carried out employing the operators 

It is found that the mean photon energy (the mean photon number) of the signal mode is twice of a twin signal light beam. And the energy fluctuations (the variance of the photon number) of the two signal light beams is four times that of one of the signal light beam. We have also shown that the photon energy (the photon number) quadrature squeezing of the output signal mode is exactly equal to that of the cavity signal mode. In light of this, the global quadrature squeezing of the signal mode is independent of the mean values. On the basis of the above results, we come to the conclusion that the quantum analysis of a one-mode sub-harmonic generation should somehow be modified.
References
- Kassahun, F. (2012) The Quantum Analysis of Light. Create Space, South Carolina.
- Anwar, J. and Zubairy, M.S. (1992) Physical Review A, 45, 1804. http://dx.doi.org/10.1103/PhysRevA.45.1804
- Daniel, B. and Fesseha, K. (1998) Optics Communications, 151, 384. http://dx.doi.org/10.1016/S0030-4018(98)00039-X
- Milburn, G.J. and Walls, D.F. (1983) Physical Review A, A27, 392. http://dx.doi.org/10.1103/PhysRevA.27.392
- Kassahun, F. (1998) Optics Communications, 156, 145. http://dx.doi.org/10.1016/S0030-4018(98)00425-8
- Plimark, L.I. and Walls, D.F. (1994) Physical Review A, A50, 2627. http://dx.doi.org/10.1103/PhysRevA.50.2627
- Walls, D.F. and Milburn, G.J. (1995) Quantum Optics. Springer-Verlag, Berlin.
- Scully, M.O. and Zubairy, M.S. (1997) Quantum Optics. Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9780511813993
- Zhan, Y. (2010) Modern Applied Science, 4, 8.
- Agarwal, G.S. and Adam, G. (1989) Physical Review A, A39, 6259. http://dx.doi.org/10.1103/PhysRevA.39.6259
- Collett, M.J. and Gardiner, C.W. (1984) Physical Review A, A30, 1386. http://dx.doi.org/10.1103/PhysRevA.30.1386
- Lugiato, L.A. and Stkini, G. (1982) Optics Communications, 41, 67. http://dx.doi.org/10.1016/0030-4018(82)90215-2
- Walls, D.F. and Barakat, R. (1970) Physical Review A, A1, 446. http://dx.doi.org/10.1103/PhysRevA.1.446
- Milburn, G.J. and Walls, D.F. (1981) Optics Communications, 39, 401.

