Journal of Modern Physics
Vol. 4 No. 9 (2013) , Article ID: 37439 , 8 pages DOI:10.4236/jmp.2013.49164
The Spring of the Earth, the Sun and the Universe
Fisica Laboratorio, TIS, Block K Macau University of Science and Technology, Macau, China
Email: lmtsang05@hotmail.com
Copyright © 2013 Ling Man Tsang. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received May 6, 2013; revised June 11, 2013; accepted July 8, 2013
Keywords: Cosmological Constant; Expanding Universe; Dark Matter
ABSTRACT
A spring term is added into Newton’s law of gravitation. The spring k of the earth is found to be 1.21 × 10−8/sec2. The PPN gamma is a dependence of distance r from the sun. The expanding universe is due to the cosmological constant. The Hubble constant is found to be the square root of the cosmological constant. The query of the missing dark matter in the galaxies is clarified.
1. Introduction
The true nature of the cosmological constant is still unknown, whether it is physical or purely a mathematical conjecture. Secondly, its value is so small that the value 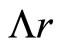 can only be significant in large-scale space. We previously suggested that each source had its own cosmological constant, which hereinafter, to be renamed as the spring constant of the source as we did previously [1,2].
can only be significant in large-scale space. We previously suggested that each source had its own cosmological constant, which hereinafter, to be renamed as the spring constant of the source as we did previously [1,2].
Consider a simple case of the Kottler form
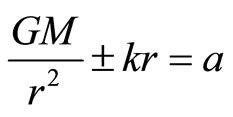 (1)
(1)
where the first term is the usual Newton’s inverse square law while the second term refers to the spring constant k of the source, for instance, the earth. The spring constant k, which can either be extended or compressed, is in fact the cosmological constant if we look at Einstein’s exterior field equations of the form
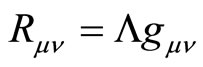 (2)
(2)
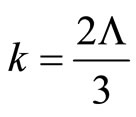
is called the spring constant because it resembles an harmonic oscillator. Obviously, the Kottler solution (1) is the result of (2). Throughout the entire paper, only the 3- dimensional case is to be considered
2. The Spring of the Earth
To be more rigorous when applying to the earth, the centrifugal acceleration  is taken into account and placed onto the left of (1). For θ = 0, the centrifugal acceleration at the equator will be maximum.
is taken into account and placed onto the left of (1). For θ = 0, the centrifugal acceleration at the equator will be maximum.
Taking:
the earth rotation ω = 7.3 × 10−5/sec;
the earth radius r0 = 6.4 × 106 m;
the earth mass = 6 × 1024 kg;
the gravity of earth =  (see Appendix).
(see Appendix).
θ = 42˚, the latitude of Massachusetts where Pound and Rebka performed their experiments at Harvard. Equation (1), including the additional negative term of the centrifugal acceleration
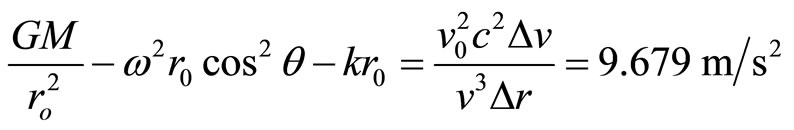 (3)
(3)
The third term is usually referred to the fifth force as suggested by Fischbach et al [3-5] but we have pointed out previously that the Yukawa-like fifth force will yield an unreasonable value of r at the acceleration a = 0. For an escaping object, the spring will have the same direction as gravity
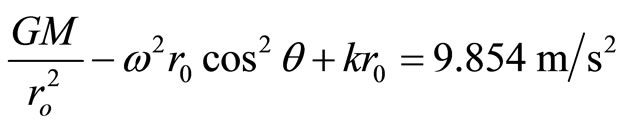 (see Appendix) (3a)
(see Appendix) (3a)
The first two terms of (3) and (3a) give the value of 9.7516 m/s2. Hence,
 (3)
(3)
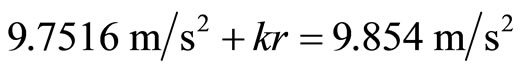 (3a)
(3a)
This is more than a coincidence to have 9.679 m/s2 smaller than 9.7516 m/s2 in (3) and 9.854 m/s2 larger than 9.7516 m/s2 in (3a). Both equations yield the result of k = 1.21 × 10−8/s2.
Of course, one can argue that the percent level of accuracy can also disprove (3) and (3a). Upon substituting the above value of k into (1) and setting a = 0, we have r = R = 32,000 km where such a spherical shell is gravity-free. This R is the maximum extension, and beyond this critical extension, only Newton’s inverse law remains effective. To express mathematically:

The spring force is the type of intermediate range. Springs are the aether that fill up the entire space and attach onto the source. Galaev found aether to be a compressible viscous gas having the kinematic viscosity of 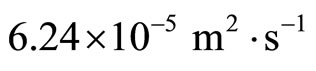 [6]. However, we are not in favor of such a aether wind concept. Axion is not spring since it can be produced in the core of the sun via the Primakoff effect.Then it travels to the earth where by interacting with a transverse magnetic field and detected by an X-ray detector. Similarly, the Poher’s universon particle travelling at the speed of light [7,8] is not our proposed spring. However, the above three particles namely, the Galaev gas, axions and the universons travel through the spring. Our earth carries the spring aether while revolving around the sun, causing the null result of the Michelson-Morley experiments.
[6]. However, we are not in favor of such a aether wind concept. Axion is not spring since it can be produced in the core of the sun via the Primakoff effect.Then it travels to the earth where by interacting with a transverse magnetic field and detected by an X-ray detector. Similarly, the Poher’s universon particle travelling at the speed of light [7,8] is not our proposed spring. However, the above three particles namely, the Galaev gas, axions and the universons travel through the spring. Our earth carries the spring aether while revolving around the sun, causing the null result of the Michelson-Morley experiments.
3. The Spring of the Sun
We had included the spring term in the Binet’s equation but found that the spring constant of the sun varied from 10−16 to 10−21/sec2 (See Table 1). Furthermore, by comparing with some other authors, our obtained spring constant within the inner planets seems to be more reasonable. Later in this paper Section 8, we explain how the spring of the sun being obtained.
We need to point out that by solving the Binet’s equation, the spring of the sun does not affect the perihelion shift of a planet but this spring will affect the light deflection in the form of [1]:

Table 1. Different values of the sun’s spring constant k (sec−2).
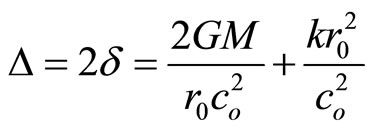 (4)
(4)
where the velocity of light is co (co ≤ c), implying the speed of light runs slower under the influence of gravity. Since the deflection
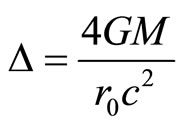 (5)
(5)
is well established in general relativity, we shall add this spring term into (5) to get
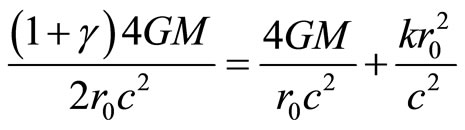 (6)
(6)
where ro = 6.95 × 108 m, k = 10−16/s2. The PPN parameter γ becomes
 (7)
(7)
Although the exact value of γ cannot be determined, most authors agree that it must be a constant near to unity. Froesche [14] pointed out that 1/2(1 + γ) = 1 within 0.1%; Bertotti [15] pointed out that ; Vecchiato [16] pointed out that |1 − γ| lies between 10−5 to 10−7; and Shapiro [17] gave the value γ = 0.9998 ± 0.0004. Nearly all authors concluded that the value of γ is a constant close to unity within the solar system. But from (7), γ depends on the distance r, even though it is not easily to be observed.
; Vecchiato [16] pointed out that |1 − γ| lies between 10−5 to 10−7; and Shapiro [17] gave the value γ = 0.9998 ± 0.0004. Nearly all authors concluded that the value of γ is a constant close to unity within the solar system. But from (7), γ depends on the distance r, even though it is not easily to be observed.
Outside the solar system the sun’s spring becomes weaker and finally breaks at r = 1013 m. From (7), the value γ is close to unity since the second term is very small. The nominal value gamma = 1 applies for pure General Relativity. Modified gravitation theories, also including additional interactions, are expressed in the Parametrised Post-Newtonian formulation with parameter values, which may be different from 1.
The amplitude of the discrepancy from unity depends on the theory. The current experimental verifications (as produced by Gai and Vecchiato’s group) are at the precision level 10−5 with Cassini, and may reach in the near future the 10−6 level with Gaia. Better measurements will constrain the theory.
4. The Spring of the Universe
The spring k of the universe in such a large scale structure can be easily explained without using higher dimensions nor vacuum as some authors suggested [18-21]. The expanding mechanism can be in the form of
 (8)
(8)
 [22]
[22]
where Ω is the negative pressure to separate matter when the spring force is acting against it. Strong evidences show that the accelerating rate is increasing [23-25]. Since none of the observable matter can produce an expanding pressure , the expansion can be due to the cosmological constant
, the expansion can be due to the cosmological constant . Ignoring the first term of (8) and all the numerical factors, from (1) we immediately yield the result of
. Ignoring the first term of (8) and all the numerical factors, from (1) we immediately yield the result of
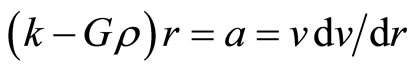 (9)
(9)
or 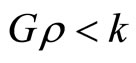
where
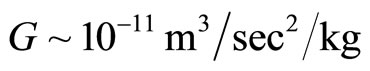
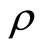 ~ 10−27 kg/m3 = mass density inside the universe.
~ 10−27 kg/m3 = mass density inside the universe.
We are aware that some authors also applied the cosmological constant in the expanding universe similar to our (9) [27]. Differently, they inserted the Hubble law into the equation rather than deduced it consequently. From (9), we immediately obtain the approximate relationship of:
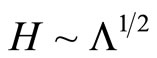 and the Hubble law
and the Hubble law 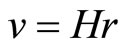
where H = Hubble constant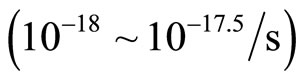 .
.
The value of H agrees with observations [see also 28-32]. We consider only the case of 3-dimensions.
Since expansion is mainly based on the red-shift and the present radius of the universe r = R ~ 10 billion light years ~ 1026 m (from P. Butterworth, NASA), an accelerating rate of R can be very useful in the study of cosmology. Equation (9) shows a non-stop universe until the spring breaks. However, this may not be the case. By choosing the present radius and density of the universe, the mass M is found to be
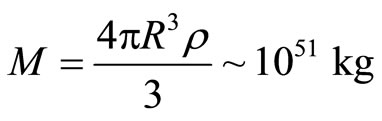
Substituting the above into (1) and set a = 0, we get
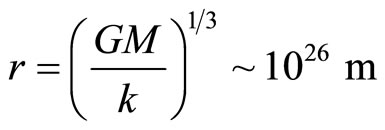
which is more or less the radius at our present time. The velocity

is less than the speed of light. The universe is expected to cease its acceleration at our present time.
5. The Missing Mass in the Rotation Curve of Galaxies
Our initial plan is to evaluate the mass and spring constant of the Coma Cluster without the aids of rotation curve but based on the assumptions that:
• the outer edge radius R of the cluster and the velocity must be known
• there is no change in velocity outside r > R and the spring is assumed to be constant outside R.
Authors including Kraft and van Leeuwer [33,34] pointed out some aberations in the observed velocity v ~ 0(106) m/s and the distance r. Zwicky [35] and Rubin et al [36] provided the first pieces of evidence that large amounts of dark matter do exist outside the visible region of most galaxies. Our present purpose is to clarify the so-called missing mass using spring theory. As a rough estimation,the core radius here can be treated as the outer edge radius of the cluster while the velocities in the following 4 papers are to be used in our calculation. The simplest way is to apply the viral theorem
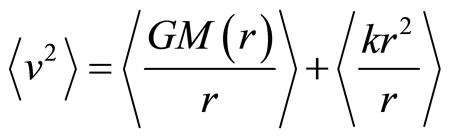 (10)
(10)
Different authors had different values of velocity v and core radius R:
1) from Zwicky [35]: v = 0.78 × 106 m/s, R = 2 × 1020 m 2) from Shao et al [37]: velocity dispersion v = 0.935 × 106 m/s, core radius R = 5.2’ = 0.936 × 1019 m 3) from Omer and Wilson [38]: R = 100’ = 1.8 × 1020 m 4) from Chincarini and Rood [39]: R = 6o = 6 × 1020 m Here, we choose 1 kpc = 3 × 1019 m throughout this paper and take the average from the above to get v = 0.85 × 106 m/s and R = 1.3 × 1020 m. The mass of the Coma Cluster of galaxies is found to be, neglecting the spring term,
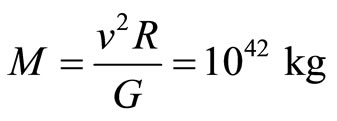 (11)
(11)
Outside the edge radius of the Cluster, the rotation curve is more or less flat, or dv/dr = 0 for r > R. The spring constant can be treated as a constant up to r = 4R even though it must be function of r. Hence we get:
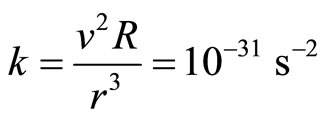 (12)
(12)
We admit our calculation above is too crude without a rotation curve. In spite of this, the existence of a spring term can explain the missing mass. Next, we look at some rotation curves. Figure 1 shows the rotation curves of 4 NGC’s [40]. We select a suitable point before the Keplerian motion on each curve:
For NGC 4594: v = 230 km/s, R = 2.7 kpc. which are obtained from the curve, whereas Zwicky gives v = 4 × 105 m/s, R = 4 × 1029 m [35].
For NGC 2590, 1620 and 7664: v = 200 km/s, R = 7.5 kpc where r = R is the outer edge radius of these NGC’s. All 4 NGC’s are found to have the same mass M ~ 1041 kg using (11). Next, we select 3 points on each curve

Figure 1. Rotation curves of NGC 4594, 2590, 1620, and 7664 [40].
from 8 kpc onwards to the right and use (10) to solve for M and the spring k. The results are
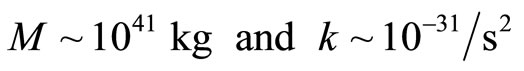 (13)
(13)
We now investigate our Milky Way. From the rotation curve of Figure 2, we select two suitable points between the D and B curves [41]:
200 km/s, r = 8 kpc and 170 km/s, r = 15 kpc To solve for (10). we get:
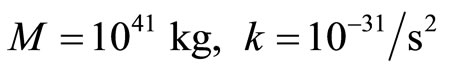 (14)
(14)
Each mass can only have one unique spring constant assigned to it. Comparing (11), (12), (13) and (14), we can deduce that for M = 1041 kg, k = 10−31/s2.
6. On the Rotating Universe
Since Goedel’s proposal of a rotating universe in 1949, numerous authors gave different values of the angular velocity of the universe (ω rad/yr). These values were based on the cosmic microwave background, or on Einstein’s field equations. Some of their values are selected as Table 2.
In spite of the discrepancies among these authors, the limit of the angular velocity can still be estimated. Along the equator of the universe, where the centrifugal acceleration is maximum, we have:
 (15)
(15)
The third term of the above equation can be ignored. Upon integration of the above, we get:
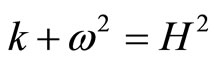
Since the Hubble constant is the square root of the cosmological spring constant, the value of the angular velocity should be limited to:
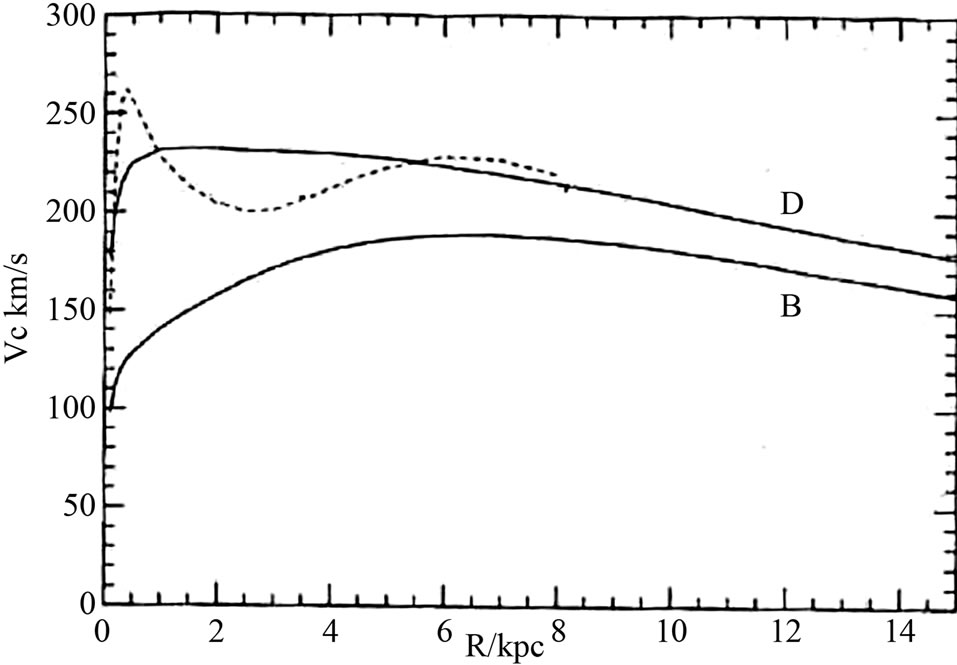
Figure 2. Circular speed versus radius of our galaxy; curve D for de vaucouleurs and Pence; curve B for Bathcall and Soneira (Binnney & Tremaine 1987) [41].
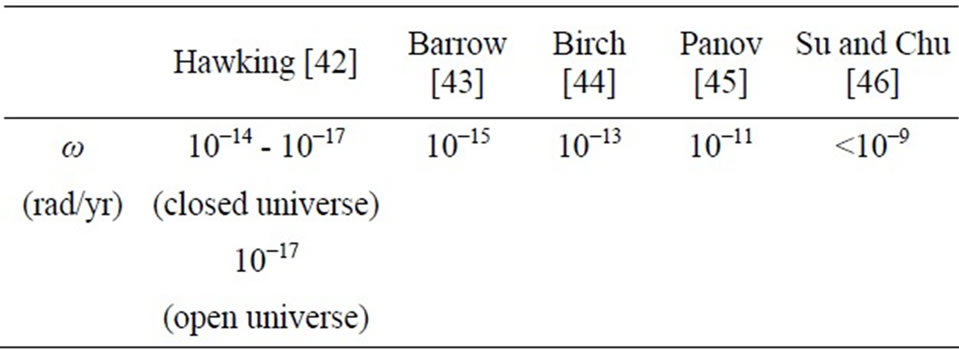
Table 2. Different values of ω from various authors.
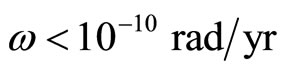
where .
.
Since the radius of out universe from previous Section 4 is ~1026 m, the speed at the outer rim will be <108 m/s, or less than the speed of light. This appears to be reasonable but problem arises: The centrifugal force along the axis of rotation will be zero. (15) can then be reduced to:

Same as (9) which differs from (15) and should be detected. There is a problem to locate the axis of rotation. One finds no difficulty to produce an angular speed. For example, ![]() can be postulated from the total derivative of the position r in the vector form of:
can be postulated from the total derivative of the position r in the vector form of:

which is, of course, meaningless. We suggest an isotropic, homogeneous and non-rotating universe which agrees with the Big Bang and Causality.
7. The Electric Field
The electric field energy density surrounding a charge q is proportional to the square of the field intensity E, or
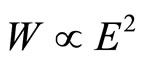 (16)
(16)
Since a charge is always accompanied by its electromagnetic mass δm, the total mass becomes M = mechanical mass + electromagnetic mass δm (17)
The above two masses on the right side of (17) are non-separable from each other. The surrounding electric field energy, according to Gauss law, should be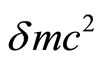 . Equation (16) can be re-written as
. Equation (16) can be re-written as
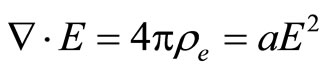 (18)
(18)
where ![]() is a constant to be determined. Upon integration, we have
is a constant to be determined. Upon integration, we have
 (19)
(19)
where A, B are the constants of integration. By setting A be the charge q, (16) becomes
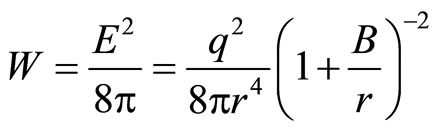 (20)
(20)
The total electric field energy over the whole space is
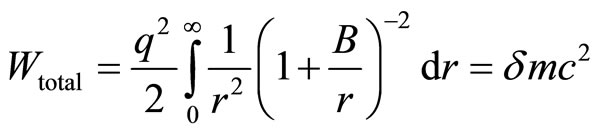 (21)
(21)
which is the Gauss law. Thus,
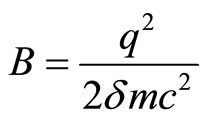 (22)
(22)
The field intensity becomes
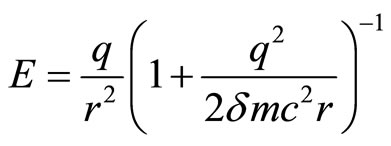 (23)
(23)
The potential can be written as
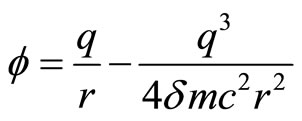 (long range) (24)
(long range) (24)
 (short range) (25)
(short range) (25)
In short range, A, B need to be determined eventhough (25) has the form as (31) of [47]. Obviously, for δm → 0, E → 0, indicating that the electromagnetic mass always accompanies with the charge.
We can use the Bohr model of an atom to find the value of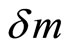 . The force equation, the energy equation and the conservation of angular momentum can be written as, respectively,
. The force equation, the energy equation and the conservation of angular momentum can be written as, respectively,
 (26)
(26)
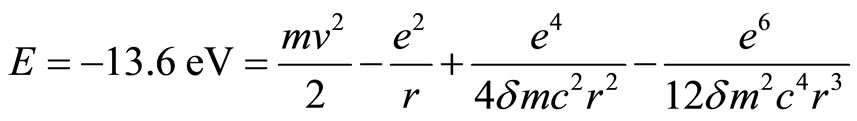 (27)
(27)
and
 (28)
(28)
in which m is the rest mass of the orbiting electron. Combing (26) and (28), we obtain
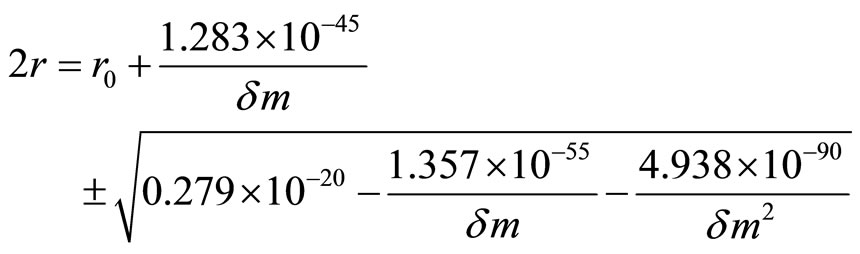 (29)
(29)
where the first term ![]() is the Bohr radius. Upon solving (26) and (27), we have
is the Bohr radius. Upon solving (26) and (27), we have
 (30)
(30)
There are several solutions from (19) and (30) among which we roughly estimate
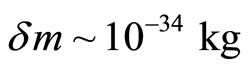
which is more or less the value of an electron neutrino. If this is true, an electron is a composite particle.
8. The Gravitational Field
In analogy to the electric field, the gravitational field energy (21) can be written as
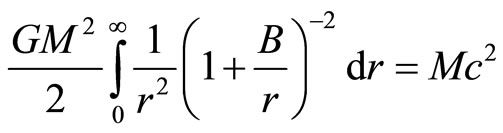 (31)
(31)
where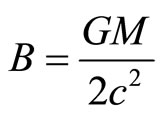 . The field intensity (19) can be written as
. The field intensity (19) can be written as
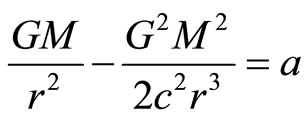 (long range) (32)
(long range) (32)
Again, in short range gravitational field, the value of A, B in (25) need to be determined. The Binet equation of a planet becomes
 (33)
(33)
where h, u are the conservation of angular momentum and the reciprocal of r respectively. By solving (33), we obtain the perihelion shit of
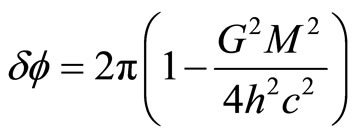
which, of course, is much smaller than the result of general relativity. However, we are able to find the spring of the sun 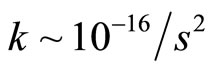 as shown in the table of Section 3.
as shown in the table of Section 3.
9. Short Range Interactions
It is known that once the mass approaches or lesser than the Planck mass of 10−8 kg, gravity becomes strong interaction and the potential energy depends on the distance of the two interacting particles only. Consider the proton-electron electric interaction, the energy level of Bohr’s atom −13.6 eV does not agree with 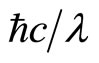 and hence, the term
and hence, the term 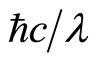 refers to very short distance and most probably, the spring energy
refers to very short distance and most probably, the spring energy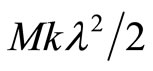 . Equation (25) can be rewritten as
. Equation (25) can be rewritten as
 (34)
(34)
It is not reasonable to set  in very short electric or gravitational interaction since there exists a big amount of energy and there are heavy particles inside the nucleus. Equation (34) belongs to the source of a nucleon, hence the spring energy of a boson oscillating along
in very short electric or gravitational interaction since there exists a big amount of energy and there are heavy particles inside the nucleus. Equation (34) belongs to the source of a nucleon, hence the spring energy of a boson oscillating along ![]() gives
gives
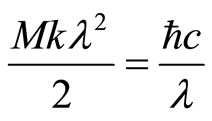 = energy of meson (35)
= energy of meson (35)
where M is tentatively set to be the mass of the testing nucleon.
For λ = 1.5 fm, mass of pi-meson mπ = 132 MeV and 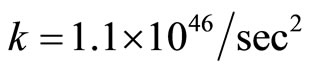 is the spring linking the 2 nucleons. A simple explanation of why larger mass has weaker spring and smaller mass has stronger spring is that: if two particles are connected by N identical springs each of k1, the combined spring constant will become
is the spring linking the 2 nucleons. A simple explanation of why larger mass has weaker spring and smaller mass has stronger spring is that: if two particles are connected by N identical springs each of k1, the combined spring constant will become
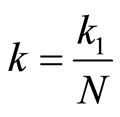 (36)
(36)
where N is greater at longer distance and so the spring is weaker. Equation (36) only refers to a single line of force connecting two interacting bodies. We are not sure whether if a unit spring k1 has the Planck length.
The β decay can be explained 3 dimensionally as that one of the springs is released from compression with its one end attaching to the nucleus while the other free end pushing an electron outwards; a process similar to the expanding universe where the gravitational force cannot hold the matter from flying out. From (35), the spring energy on the left equals to the energy of a W boson. The spring kicked out an electron, exerting an energy of 80 GeV, which is much greater than that of an electron. This excited electron, upon the acceptance of a transfer of momentum from the spring, will release an anti-electron neutrino. Such a mechanism of kicking out an 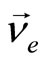 is performed by a spring with its one end attaching onto the electron while the other free end pushing the
is performed by a spring with its one end attaching onto the electron while the other free end pushing the 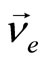 out of the electron. We have no idea why an electron neutrino turns out to be an anti-neutrino after leaving the electron.The energy of such a spring is 90 GeV, which also known as the Z boson.
out of the electron. We have no idea why an electron neutrino turns out to be an anti-neutrino after leaving the electron.The energy of such a spring is 90 GeV, which also known as the Z boson.
Theorem In short range interaction. The spring 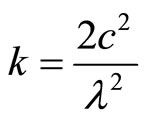 where
where
![]() is the length of the spring.
is the length of the spring.
10. Conclusion
We admit that most of our numerical values in this paper are approximate since our main purpose is to introduce the spring term into the theory. By comparing the spring of the earth, (10−8/s2), the sun (10−16/s2), galaxies of M = 1041 kg (10−31/s2) and the universe (10−35/s2), we show that the larger the mass, the lesser is the value of k. Conversely, the spring between 2 nucleons is found to be 1.1 × 1046/sec2. The myth of the fifth force, aether, the missing mass in the galaxies, dark matter, Hubble constant and the cosmological constant and all these problems can be solved by a simple 3 dimensional “spring”. There are rooms for the spring theory to fit into particle physics. Our present work gives a start.
11. Acknowledgements
The author wishes to thank Professor Mario Gai of The Instituto Nazionale di Astrofisica for his valuable ideas in the PPN gamma.
REFERENCES
- L. M. Tsang, Canadian Journal of Pure and Applied Sciences, Vol. 4, 2010, pp. 1973-1979.
- L. M. Tsang, New Astronomy, Vol. 17, 2012, pp. 18-21. doi:10.1016/j.newast.2011.05.004
- E. Fischbach and C. Talmadge, Nature, Vol. 356, 1992, pp. 207-215.
- E. Fischbach, et al., Physical Review Letters, Vol. 56, 1986, pp. 3-6. doi:10.1103/PhysRevLett.56.3
- R. H. Sanders, Astronomy & Astrophysics, Vol. 136, 1984, pp. 21-23.
- Y. M. Galaev, Spacetime & Substance, Vol. 5, 2002, pp. 207-224.
- C. Poher and D. Poher, Applied Physics Research, Vol. 3, 2011, pp. 51-66. C. Poher and P. Marquet, Applied Physics Research, Vol. 4, 2012, pp. 120-127.
- J. Consiglio, Applied Physics Research, Vol. 4, 2012, pp. 144-158. doi:10.5539/apr.v4n2p144
- P. Jetzer, M. Sereno, Physical Review D, Vol. 73, 2006, Article ID: 044015.
- J. F. Cardona and J. M. Tejeiro, The Astrophysical Journal, Vol. 493, 1998, pp. 52-53. doi:10.1086/305125
- L. Iorio, International Journal of Modern Physics D, Vol. 15, 2006, pp. 473-475.
- G. S. Adkins and J. McDonnell, Physical Review D, Vol. 75, 2007, Article ID: 082001.
- G. S. Adkins, J. McDonnell and R. N. Fell, Physical Review D, Vol. 75, 2007, Article ID: 064011. doi:10.1103/PhysRevD.75.064011
- M. Froesche, F. Mignard and F. Arenau, Proceedings from the Hipparcos Venice 97’ Symposium, ESA, Noordwijk, 1997.
- B. Bertotti, L. Iess and P. Tortora, Nature, Vol. 425, 2003, pp. 374-375. doi:10.1038/nature01997
- A. Vecchiatto, et al., Astronomy & Astrophysics, Vol. 399, 2003, pp. 337-342. doi:10.1051/0004-6361:20021785
- S. S. Shapiro, et al., Physical Review Letters, Vol. 92, 2004, Article ID:121101. doi:10.1103/PhysRevLett.92.121101
- S. Foerste, et al., Journal of Cosmology and Astroparticle Physics, Vol. 7, 2011, pp. 7-23.
- S. D. Bass, Journal of Physics G: Nuclear and Particle Physics, Vol. 38, 2011, Article ID: 043201. doi:10.1088/0954-3899/38/4/043201
- P. S. Wessen, International Journal of Modern Physics D, Vol. 10, 2001, pp. 905-912. doi:10.1142/S0218271801001396
- B. Mashoon and P. S. Wessen, Classical and Quantum Gravity, Vol. 21, 2004, p. 3611. 0doi:10.1088/0264-9381/21/14/020
- M. Tegmark, et al., Physical Review D, Vol. 69, 2004, Article ID: 103501. doi:10.1103/PhysRevD.69.103501
- S. Perlmutter, et al., Astrophy Journal, Vol. 517, 1999, pp. 565-586.
- S. Perlmutter, Physics Today, Vol. 56, 2003, p. 53. doi:10.1063/1.1580050
- A. Riess et al., Astronomical Journal, Vol. 116, 1998, pp. 1009-1038. A. Riess, et al., Astrophysical Journal, Vol. 607, 2004, pp. 665-687. doi:10.1086/383612
- H. Ruchwanger, Applied Physics Research, Vol. 3, 2011, pp. 110-129.
- A. Bonasera, Journal of Modern Physics, Vol. 3, 2012, pp. 1722-1726. doi:10.4236/jmp.2012.311212
- W. L. Freedman, Physics Reports, Vol. 333-334, 2000, pp. 13-31.
- W. L. Freedman, Physics Reports, Vol. 307, 1998, pp. 45- 51. doi:10.1016/S0370-1573(98)00073-8
- H. E. Froehlich, Astronomische Nachrichten, Vol. 308, 1987, pp. 169-171. doi:10.1002/asna.2113080302
- M. Křížek, New Astronomy, Vol. 17, 2012, pp. 1-7. doi:10.1016/j.newast.2011.05.003
- P. Nugent, et al., Physical Review Letters, Vol. 75, 1995, pp. 394-397. doi:10.1103/PhysRevLett.75.394
- R. P. Kraft, The Astrophysical Journal, Vol. 142, 1965, pp. 681-702. doi:10.1086/148330
- F. van Leeuwen and R. S. Le Poole, “Flattening Rotation, Inclination and Mass of Omega Centauri,” Astrophysics ASP Conference Series 265, 2002, pp. 41-50.
- F. Zwicky, The Astrophysical Journal, Vol. 86, 1937, pp. 217-246. doi:10.1086/143864
- V. C. Rubin, et al., The Astrophysical Journal, Vol. 238, 1980, pp. 471-487. doi:10.1086/158003
- Z. Y. Shao, J. L. Zhao and R. S. Pan, Chinese Journal of Astronomy and Astrophysics, Vol. 18, 1994, pp. 168-177. doi:10.1016/0275-1062(94)90098-1
- G. C. Omer and A. G. Wilson, Astronomy Journal, Vol. 70, 1965, pp. 440-445. doi:10.1086/109759
- G. Chincarini and H. J. Rood, Nature, Vol. 257, 1975, pp. 294-295. doi:10.1038/257294a0
- R. C. Bless, “Discovering the Cosmos,” University Science Books, 1996, p. 461.
- J. Binney and S. Tremaine, “Galactic Dynamics,” Princeton University Press, Princeton, 1987, p. 87.
- S. Hawking, “On the Rotating Universe,” MNRAS 142, 1969, pp.129-141.
- J. D. Barrow, et al., “Universal Rotation-How Large Can It Be?” MNRAS 213, 1985, pp. 917-943.
- P. Birch, Nature, Vol. 298,1982, pp. 451-454.
- V. F. Panov, Journal of Theoretical and Applied Physics, Vol. 28, 1985, pp. 18-20.
- S. C. Su, M and C. Chu, Astrophy Journal, Vol. 703, 2009, pp. 354-361.
- J. Hynecek, Applied Physics Research, Vol. 4, 2012, pp. 44-57.
Appendix
The Jefferson Physical Laboratory at Harvard used a 57Fe source being placed at a height of 22.6 m above the detector. Gamma photons dropped to the detector. The original purpose of this Pound-Rebka experiment was to demonstrate the effect of photonic mass under the earth’s gravity. The data can be found in many textbooks (see Gravitation by Misner/Thorne/Wheeler):
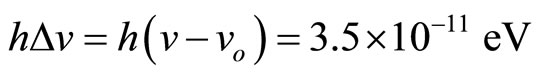
Δr = height dropped 22.6 m E = hvo the source energy 14.4 keV where h = Planck’s constant Like any other particles, a falling photon changes its frequency in the form of
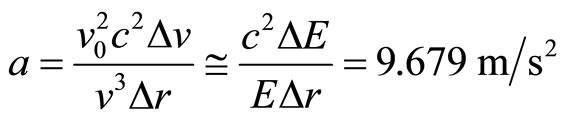
Same as (3) which is only true at Harvard, or likewise the State of Massachusetts.
In 1965 Pound and Snider refined the apparatus so that the energy shifts on the upward and downward path gave a measured difference of
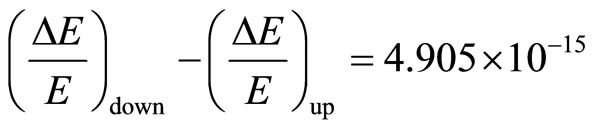 (37)
(37)
Since the first term of (37) is known, the second term will immediately yield the deceleration of 9.854 m/s2 (same as Equation (3a)).

