Journal of Modern Physics
Vol.4 No.8(2013), Article ID:35813,5 pages DOI:10.4236/jmp.2013.48148
Study of 12CC Collisions at 4.5 A GeV to Define Centrality
1Department of Basic Sciences, Riphah International University, Islamabad, Pakistan
2Department of Physics, International Islamic University, Islamabad, Pakistan
Email: *zafar_wazir@yahoo.com
Copyright © 2013 Z. Wazir et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received April 24, 2013; revised May 30, 2013; accepted July 4, 2013
Keywords: Random Matrix Theory; Nearest-Neighbor Energy Spacing Distributions; Spacing Correlations; Central Collisions; Charged Particles Multiplicity
ABSTRACT
Using a statistical method which is based on random matrix theory, the results for the nearest-neighbor energy spacing distributions E(S) obtained from experimental as well as from computational data have been selected for review study. The obtained results confirm that the energy spacing correlation between secondary charged particles depends upon the charged particles multiplicity and central collisions are also associated with charged particles multiplicity.
1. Introduction
The creation of new phases of strongly interacting matter is the most interesting area of research for physicist for last many years. Physicists are interested in studying characteristics of newly formatting matter under extreme conditions [1-7]. One way to create these new phases is the heavy ion collision at relativistic and ultra relativistic energies. We are interested in centrally dependence of hadron—nucleus and nucleus—nucleus collisions. These experiments indicate the regime change at some values of the centrality as some critical phenomena. If the regime change observed in the different experiments takes place unambiguously twice, this would be the most direct experimental evidence to a phase transition from hadronic matter to a phase of deconfined quarks and gluons [1-7]. After point of regime change the saturation is observed. The simple models cannot explain the effect.
To trace anticipated order of the phase evolution, for example, with increase of the baryon density, one analyses various characteristics of particle production at nuclear-nuclear collisions depending on the centrality of collisions [8-13]. However, there is an ongoing discussion about how to define the centrality experimentally [1-13]. For instance, in various experiments the centrality is defined as a number of protons, projectile and target fragments, slow particles, all particles, as the energy flow of the particles with emission angles equal 0˚ or 90˚, etc. [1-10]. Among the most popular approaches, based on geometrical picture, is a Glauber modeling which contains some theoretical approximations [14]. This approach enables one to establish approximately the centrality with the aid of the impact parameter b and the multiplicity of identified secondary charged particles in experiments. Note, in this case, however, there is a model dependent definition of the centrality. Evidently, the absence of an unambiguous criterion for the centrality may significantly affect the interpretation of experimental results and, therefore, hide a true signal on the onset of a new phase of the hadronic matter. In a preliminary report [15] it is suggested that tools from Random Matrix Theory (RMT) [16-22] might be useful in illuminating the presence of correlations in the spectral (momentum) distribution of secondary particles produced in nucleusnucleus collisions at high energy [18-22]. It is noteworthy that during the last twenty years the RMT grew into the powerful new statistical theory of fluctuations in a variety of physical problems [19-22]. In various fields, the Dyson-Mehta statistical measures are most often used to quantify a system’s correlations and to determine what information the fluctuations contain. These measures do not depend on the background of measurements and used in the context of RMT give universal forms depending only on the fundamental symmetries preserved [19-22]. Their only requirement is that local mean densities (or secular behaviors) be understood and their effects be removed. Furthermore, a change of fluctuation properties of a system under consideration, induced by a change of its symmetry properties, can be detected by the RMT tools unambiguously. Therefore these tools could provide a way of detecting the transition between different phases (with different fluctuation properties) of strongly interacting matter. Evidently, that the energy of secondary particles produced in nucleus-nucleus collisions at high energies is given by continuous distributions. Since in each event only a finite number of particles are emitted, the discreteness naturally comes in the analysis of data [19,22]. The average number of particles per unit of energy can change with increase (decrease) the absolute value of the energy and its direction in each event. However; it is always possible to define regions where the mean particle density is approximately a constant. On the other hand, the distance between two successive particles can fluctuate differently in different energy windows. And this characterizes the local fluctuation properties of the system. The astonishing thing is that the fluctuating properties quite different systems are determined only by over-all symmetries of system [17]. This fact provides the basis for application of the RMT tools for analysis of nucleus-nucleus collision data at high energies [15-22].
Indeed, one can find a good agreement between the results obtained in this way and a standard analysis based on the method of effective mass spectra and two-pair correlation function often used in high energy physics [18]. The purpose of the present review is to discuss a novel criterion for the centrality of collision, using a rigorous mathematical framework of the RMT [18-22]. Section 2 briefly reviews how to detect the manifestation of correlations with the aid of nearest-neighbor spacing energy distribution (NND) from the data obtained in light nuclei collisions in Dubna Experiments. Section 3 is devoted to determination of the centrality of the nucleusnucleus collisions with the aid of the NND. The main conclusions are summarized in Section 4.
2. Basic: Nearest-Neighbor Energy Spacing Distribution
The experimental data [23-25] that have been obtained from the 2-m propane bubble chamber of the Laboratory of High Energy, JINR have been used. In this experiment, there are 37792 12CC interaction events at energy of 4.5 A GeV (for greater discussion of the details see [23-26]) containing 7740 events with more than ten tracks of charged particles.
In general [18-22], this procedure does not involve any uncertainty or spurious contributions and deals with a direct processing of physical data.
One can recall that the RMT theory [14-16] deals with the Hamiltonian that belongs to an ensemble of random matrices that are consistent with the fundamental symmetries of the system. In particular [15-22], since the nuclear interaction preserves time-reversal symmetries, the relevant ensemble is the Gaussian Orthogonal Ensemble (GOE). When the time-reversal symmetry is broken one can apply the Gaussian Unitary Ensemble (GUE). The GOE and GUE correspond to ensembles of real symmetric matrices and of Hermitian matrices, respectively. Besides these general symmetry considerations, there is no need in other properties of the system under consideration.
If the “events” [18-22] are independent, i.e., correlations in the system under consideration are absent, the form of the histogram must follow E(S) = exp(−S) known as the Poisson density. The Poisson spectrum corresponds to the dominance of many crossings between different energies. On the other hand, if the levels are repelled, the density is approximately given by the Wigner surmise form E(S) = 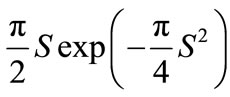 for the GOE. In turn, the crossings are usually observed when there is no mixing between states that are characterized by different good quantum numbers, while the anti crossings signal about a strong mixing due to a perturbation brought about by either external or internal sources[27]. In other words, any correlations that produce the deviation from the regular pattern (Poisson distribution): production of a collective state (resonance), or some structural changes in the system under consideration would be uniquely identified from the change of the histogram shape [27].
for the GOE. In turn, the crossings are usually observed when there is no mixing between states that are characterized by different good quantum numbers, while the anti crossings signal about a strong mixing due to a perturbation brought about by either external or internal sources[27]. In other words, any correlations that produce the deviation from the regular pattern (Poisson distribution): production of a collective state (resonance), or some structural changes in the system under consideration would be uniquely identified from the change of the histogram shape [27].
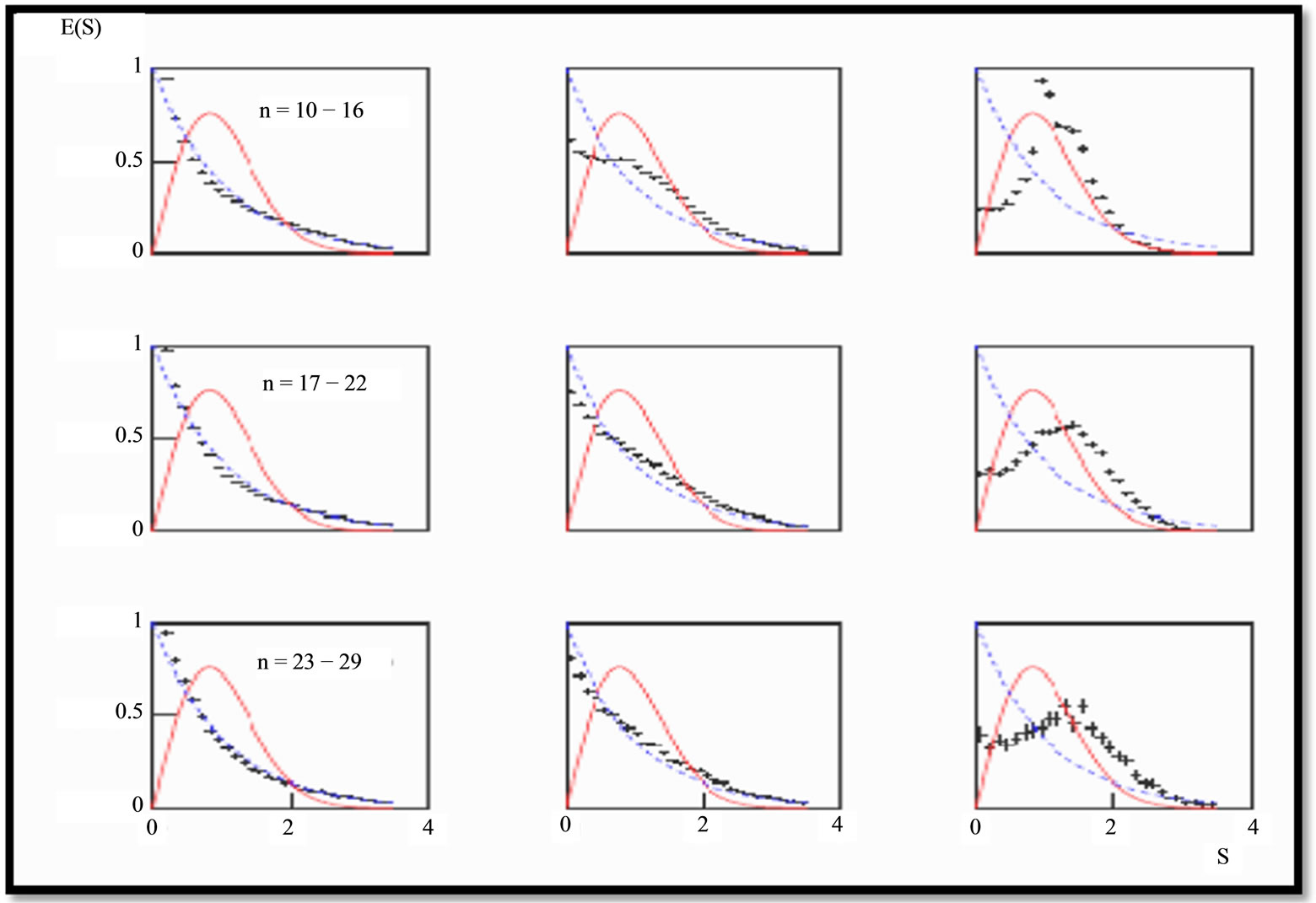
To clearly recognize correlations the total set of spacing’s {Si} has been divided into three sets, in correspondence with three regions of the measured energies: a) 0.1 < |E| < 1.18 GeV(region I); b) 1.18 < |E| < 4.0 GeV (region II); c) 4.0 < |E| < 8.5 GeV (region III) (see Figure 1). The region boundaries were determined with the requirement that the shape of the spacing density E(S) does not change in the region under consideration [19-22]. Therefore, in the present review only the total nearest-neighbor energy spacing distribution, related to all charged secondary particles is considered.
To precede further additionally the events have been separated into three groups: 1) the events with n = 10 − 14 secondary charge particles; 2) the events with n = 15 − 19 secondary charge particles; 3) the events with n = 20 − 22 secondary charge particles. In this case the separation was also done according to the criteria discussed above [19-22].
One evidently recognizes the onset of correlations for n = 10 − 14 secondary charged particles with the increase of the absolute value of the energy distribution (see Figure 1, top row, from left to right). The onset of correlations in the interval 1.18 < |E| < 4.0 GeV (the region II),

Figure 1. (Color online) the experimental (data related to all charged secondary particles) nearest-neighbor energy spacing distribution (histogram) E(S) for different regions of measured energies: the first column corresponds to 0.1 < |E| < 1.18 GeV; the second column corresponds to 1.18 < |E| < 4.0 GeV; the third column correspond to 4.0 < |E| < 8.5 GeV. The NND distribution for different multiplicities n: the top row corresponds to n = 10 − 14; the middle row corresponds to n = 15 − 19: the bottom row corresponds to n = 20 − 22. The Poisson and the Wigner surmise distributions are connected by dashed and solid lines, respectively.
found in virtue of the RMT analysis, owes their origin to the protons produced as a result of decays of well known ∆++—isobars with masses m∆++ = 1.232 and 1.650 (GeV/c2). The presence of the sharp peak in the third interval 4.0 < |E| < 8.5 GeV (the region III) can be attributed to the interaction between stripping protons in the final state, which dominates in the peripheral collisions which have been seen in P(S) distributions[19-22].
Indeed, one can find that strong correlations are brought about by the protons pairs with zero angle in the energy distribution interval 4.0 < |E| < 8.5 GeV. This interpretation becomes even more convincing with the increase of charged particles number (n = 15 − 19 and n = 20 − 22; see Figure 1, right column). With the increase of the multiplicity of secondary charge particles the number of the stripping protons decreases. As a result, the correlations, brought about by these proton pairs, decrease as well. For the multiplicity n = 20 − 22 the distribution is neither the Poisson nor the Wigner surmise. Note, however, that the number of participants is increased, which can be associated with the onset of the central collisions.
3. Determination of the Centrality Windows
To shed light on the production of the secondary charged particles, Dubna Cascade Model [1,21] is used which is the host of models those are proposed to explain the general features of relativistic nucleus-nucleus collisions. Dubna Cascade Model (DCM) is the most popular model. It is an approach based on simulation (Monte-Carlo techniques) and applied to situation where multiple scattering is important. In the simplest approach, it is assumed [21] that due to the interaction of a projectile hadron with one of the target nucleons the creation of a new particle takes place. The participating target nucleon accepts momentum and begins to move in the nucleus. All moving (cascade) particles can interact with other nuclear nucleons to produce new particles or suffer elastic rescattering. Therefore, cascade reproduction of moving particles is assumed. The interactions between cascade particles are omitted as a rule. The process continues until all moving particles either leave the nucleus or are absorbed. In the case of (A + A) collisions, it is assumed that cascade particles can interact with projectile and target nucleons. Due to analysis fast particles and correlations between slow and fast particles DCM [28-33] was recognized as the best model applied in the intermediate energy physics [34,35]. Simulating the secondary charged particles production in 12C + 12C collisions at energy of 4.5A GeV, the same procedure as for the analysis of experimental data was applied. Surprisingly, the results obtained with the aid of the DCM nicely reproduce the tendency observed for the experimental data. The model results as shown in Figure 2 confirm the existing of some peaks in the region II and their transformation to the Wigner distribution in the region III. Evidently, the model results demonstrate the existing of some non-trivial non-kinematic correlations for the secondary charged particles in the regions II and III.
This fact provides a hope that the RMT could be useful for analysis of experimental results obtained in heavy ion reactions at high energies [15-22].
This analysis provides the basis to identify the critical multiplicity that would signal on the onset of central collisions [19-22]. To this aim the DCM code [36], is used which is most suitable for the data obtained in the Dubna experiment.
4. Summary
Using the experimental data on 12CC interaction events at energy of 4.5 A GeV obtained from the 2-m propane bubble chamber of the Laboratory of High Energy, JINR, the energy distribution of the secondary charged particles produced in this reaction is analyzed and compared with the momentum distributions [19-22]. To this aim the NNDs are calculated in three intervals of the energy distributions: 0.1 < |E| < 1.18 GeV; 1.18 < |E| < 4.0 GeV; 4.0 < |E| < 8.5 GeV similarly to momentum distributions in [19-22]. To establish the connection between the NNDs and the onset of region of central collisions employed the DCM code. The results obtained with version of the DCM code evidently demonstrate that the NND enable one to detect the presence of correlations, brought about by various new mechanisms. Based on these results, one can propose novel criteria to define the centrality of the nucleus-nucleus collisions, using the NNDs for different multiplicities. In turn, the centrality of nucleus-nucleus collisions is associated with the absence of correlations.
5. Acknowledgements
We acknowledge Riphah Academy of Research & Education (RARE), Riphah International University Islamabad, Pakistan for financial support.
REFERENCES
- Z. Wazir, M. K. Suleymanov, O. B. Abdinov, E. U. Khan, M. Q. Haseeb, M. Ajaz, K. H. Khan and Sh. Ganbarova, Azerbaijan Journal of Physics (Fizika), Vol. 16, 2010, pp. 75-78.
- Z. Wazir, M. K. Suleymanov, O. B. Abdinov, E. U. Khan, M. Q. Haseeb, M. Ajaz, K. H. Khan and Sh. Ganbarova, Azerbaijan Journal of Physics (Fizika), Vol. 16, 2010, pp. 85-88.
- K. H. Khan, M. K. Suleymanov, O. B. Abdinov, Z. Wazir, E. U. Khan, M. Q. Haseeb, M. M. Ajaz and Sh. Ganbarova, Azerbaijan Journal of Physics (Fizika), Vol. 16, 2010, pp. 474-477.
- B. Z. Belashev, M. K. Suleymanov, S. Vokal, J.Vrlakova, M. Ajaz, A. Zaman, K. H. Khan and Z. Wazir, Chinese Physics C, Vol. 35, 2011, pp. 1095-1099. doi:10.1088/1674-1137/35/12/003
- M. K. Suleymanov, E. U. Khan, K. Ahmed, M. Q. Haseeb, F. Tahir, Y. H. Huseynaliyev, M. Ajaz, K. H. Khan and Z. Wazir, Indian Journal of Physics, Vol. 85, 2011, pp. 1047-1050. doi:10.1007/s12648-011-0128-1
- M. Ajaz, M. K. Suleymanov, O. B. Abdinov, A. Zaman, K. H. Khan, Z. Wazir and Sh. Khalilova, Azerbaijan Journal of Physics (Fizika), Vol. 17, 2011, pp. 17-20.
- M. K. Suleymanov, E. U. Khan, K. Ahmed, M. Q. Haseeb, F. Tahir, Y. H. Huseynaliyev, M. Ajaz, K. H. Khan and Z. Wazir, International Journal of Modern Physics, Vol. A24, 2009, pp. 544-548. doi:10.1142/S0217751X09044036
- J. Aichelin and K. Werner, Physical Review, Vol. C79, 2009, Article ID: 064907. doi:10.1103/PhysRevC.79.064907
- I. C. Arsene, Journal of Physics G: Nuclear and Particle Physics, Vol. 36, 2009, Article ID: 064004.
- H. Masui, The European Physical Journal, Vol. C62, 2009, p. 169.
- R. A. Soltz, R. J. Newby, J. L. Klay, M. Heffner, L. Beaulieu, T. Lefort, K. Kwiatkowski and V. E. Viola, Physical Review, Vol. C79, 2009, Article ID: 034607. doi:10.1103/PhysRevC.79.034607
- T. Gburek, Journal of Physics G: Nuclear and Particle Physics, Vol. 35, 2008, Article ID: 104131.
- H. Masui, Journal of Physics G: Nuclear and Particle Physics, Vol. 36, 2009, Article ID: 064047.
- M. L. Miller, K. Reygers, S. J. Sanders and P. Steinberg, Annual Review of Nuclear and Particle Science, Vol. 57, 2007, p. 205. doi:10.1146/annurev.nucl.57.090506.123020
- E. I. Shahaliev, R. G. Nazmitdinov, A. A. Kuznetsov, M. K. Syleimanov and O. V. Teryaev, Physics of Atomic Nuclei, Vol. 69, 2006, p. 142. doi:10.1134/S1063778806010182
- T. A. Brody, J. Flores, J. B. French, P. A. Mello, A. Pandy and S. S. M. Wong, Reviews of Modern Physics, Vol. 53, 1981, p. 385. doi:10.1103/RevModPhys.53.385
- M. L. Mehta, “Random Matrices,” 3rd Edition, Elsevier, Amsterdam, 2004.
- R. G. Nazmitdinov, E. I. Shahaliev, M. K. Syleimanov, and S. Tomsovic, Physical Review, Vol. C79, 2009, Article ID: 054905. doi:10.1103/PhysRevC.79.054905
- Z. Wazir, Chinese Physics Letters, Vol. 28, 2011, Article ID: 092503. doi:10.1088/0256-307X/28/9/092503
- Z. Wazir, Chinese Physics C, Vol. 34, 2010, pp. 1593- 1597. doi:10.1088/1674-1137/34/10/008
- Z. Wazir, R. G. Nazmitdinov, E. I. Shahaliev and M. K. Suleymanov, Chinese Physics C, Vol. 34, 2010, pp. 1076- 1081. doi:10.1088/1674-1137/34/8/007
- Z. Wazir, et al., Modern Physics Letter A, Vol. 27, 2012, Article ID: 1250090.
- O. Balea, et al., Physical Letters, Vol. B39, 1972, p. 571. doi:10.1016/0370-2693(72)90347-4
- N. Akhababian, et al., JINR Report, No. 1-12114, Dubna, 1979.
- D. D. Armutliiski, et al., Yadernaya Fizika, Vol. 45, 1987, p. 1047.
- H. N. Agakishiyev, et al., Zeitschrift für Physik C Particles and Fields, Vol. 27, 1985, p. 177.
- H. A. Weidenm¨uller and G. E. Mitchell, Reviews of Modern Physics, Vol. 81, 2009, p. 539. doi:10.1103/RevModPhys.81.539
- V. S. Barashenkov and V. D. Toneev, “Interaction of High Energy Particles and Atomic Nuclei with Nuclei,” Atomizadt, Moscow, 1972.
- N. W. Bertini, et al., Physical Review, Vol. C9, 1974, p. 522. doi:10.1103/PhysRevC.9.522
- N. W. Bertini, et al., Physical Review, Vol. C14, 1976, p. 590. doi:10.1103/PhysRevC.14.590
- J. P. Bondorf, et al., Physics Letters, Vol. 65B, 1976, p. 217.
- J. P. Bondorf, et al., Zeitschrift für Physik, Vol. A279, 1976, p. 385.
- V. D. Toneev and K. K. Gudima, Nuclear Physics, Vol. A400, 1983, p. 173. doi:10.1016/0375-9474(83)90433-5
- S. G. Mashnik, “Intermediate Energy Nuclear Data: Odels and Codes,” Proceedings of a Specialists Meeting, Paris, 1994, p. 107.
- M. B. Blann, H. Gruppelaar, P. Nagel and J. Rodens, “International Code Comparison for Intermediate Energy Nuclear Data,” NEA, OECD, Paris, 1994.
- V. S. Barashenkov, F. G. Zheregy and Zh. Musulmanbekov “Preprint JINR P2-83-117,” 1983, Dubna.
NOTES
*Corresponding author.