ABSTRACT

Previous work by Sigalotti in 2006 and recently by Hendi and Sharifzadeh in 2012 showed that all the fundamental equations of special relativity may be derived from a golden mean proportioned classical-Euclidean triangle and confirmed Einstein’s famous equation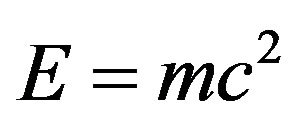. In the present work it is shown that exchanging the Euclidean triangle with a hyperbolic one an extended quantum relativity energy equation, namely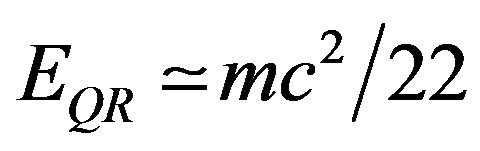, is obtained. 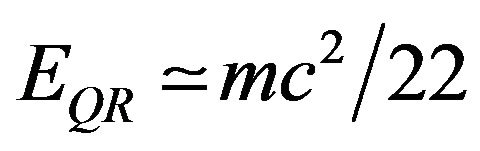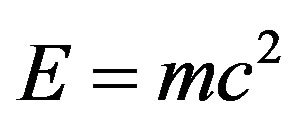The relevance of this result in understanding the true nature of the “missing” so-called dark energy of the cosmos is discussed in the light of the fact that the ratio of to is 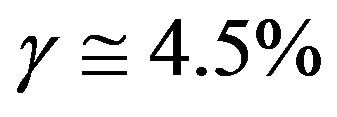which agrees almost completely with the latest supernova and WMAP cosmological measurements. To put it succinctly what is really missing is a quantum mechanical factor equal 1/22 in Einstein’s purely relativistic equation. This factor on the other hand is derivable from the intrinsic hyperbolic Cantor set nature of quantum entanglement.

1. Introduction and Background Information

In a remarkable paper by Hendi and Sharifzadeh [1] the authors used Sigalotti’s insight regarding the connection between Einstein’s special relativity and the golden mean triangle [2] to derive all the fundamental equations of Lorentz and Einstein [2,3]. This beautiful purely geometrical and completely novel derivation of the classical equations of relativity compel one to ask himself if the extended Einstein equation introduced by El Naschie [4]

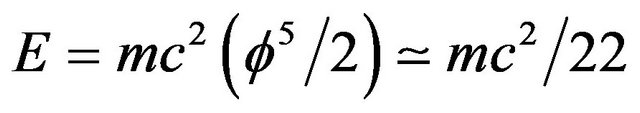(1)

could be derived or at least elucidated geometrically in an analogous way to that of Sigalotti, Hendi and Sharifzadeh [1,2]. Without writing a single equation or making a line of computation we can answer this question affirmatively. The rationale behind our confidence that this is correct is the following. Special relativity is based on the extension of Euclidean 3D spacetime geometry to also a Euclidean but 4D spacetime geometry [1-4]. However quantum relativity which unifies relativity and quantum mechanics requires a more general form of geometry [5]. This geometry is the geometry of compactified Klein’s modular curve 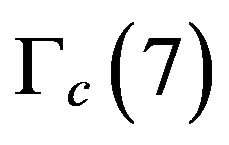[5,6]. This is nothing else but the classical modular curve of F. Klein with its 336 degrees of freedom extended to a curve with infinite but hierarchical dimensions which have a finite weight of almost 339 or more accurately 336 + 16k = 338.8854382 where 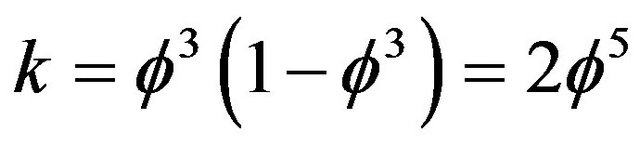and

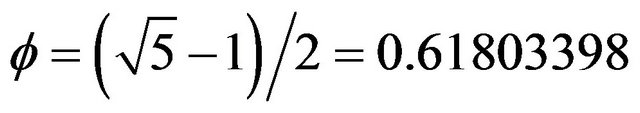is the golden mean [5,6]. This particular form of Klein modular curve is basically a collection of an infinite number of hierarchical hyperbolic triangles [5,6] and here is the deceptively simple connection. It is the geometry of these hyperbolic traingles of the compactified Klein modular curve which in an analogous way leads to the quantum-relativity extension of Einstein’s 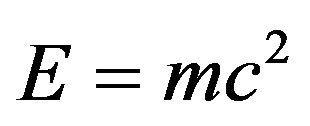to the by now relatively well known result of the ordinary energy of a quantum particle [4]

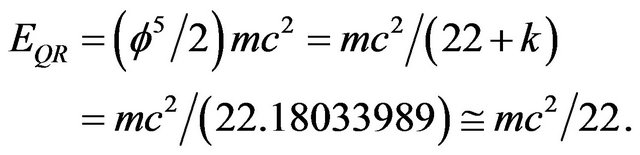(2)

One only needs to remember that the sum of the internal angles of a Euclidean triangle is 180 degrees. However for a hyperbolic triangle it takes all possible values. In particular we have 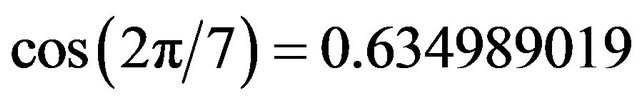which is close to the golden mean 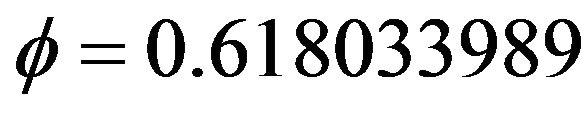and represents the triangles of Klein’s original curve while for n = 5 rather than 7, one finds the exact golden mean from.

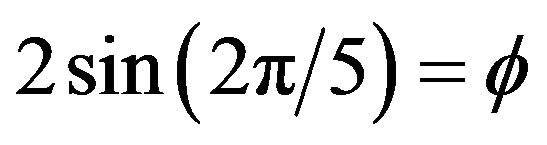2. Analysis-Relativistic Transformation

Next let us show how this result, namely 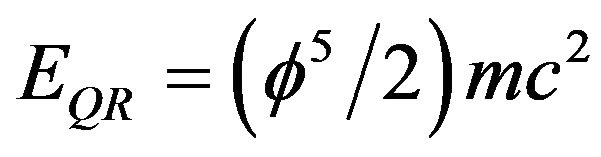, is found in a straight forward manner based on an extremely simple Lorentz-like transformation (see Table 1) with a nontrivial deep meaning. We account for the three well known relativistic effects [1- 4]:

1) Time (t) delineation;

2) Length (x) contraction;

3) Mass (m) increase.

as the velocity v tends to the speed of light c via the following boost 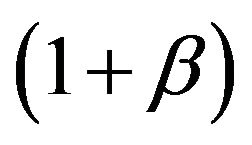and anti-boost:

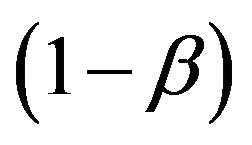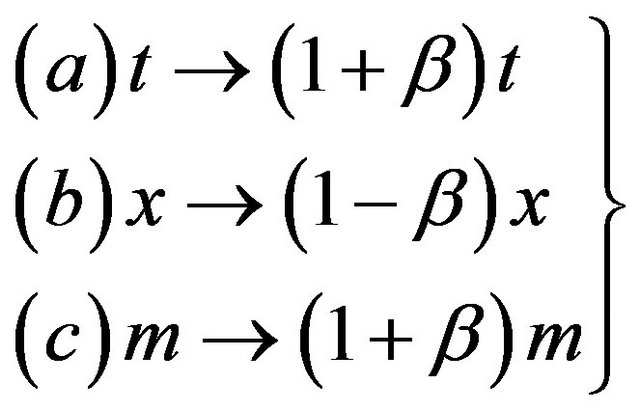(3)

Inserting in Newton’s kinetic energy

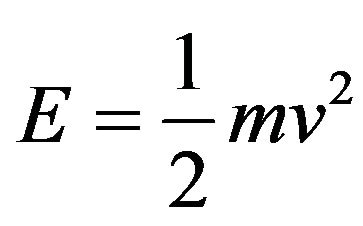(4)

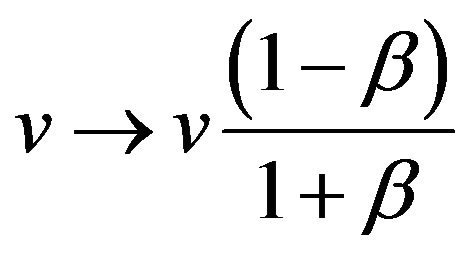and after letting and noting that one finds [4]

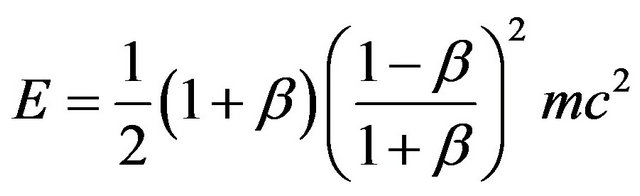. (5)

For the critical value 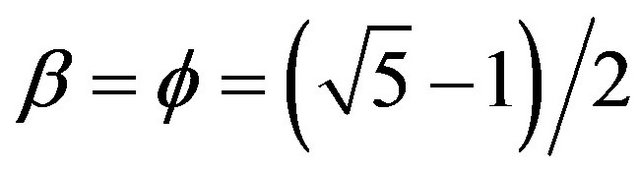which is inert to the compactified Klein modular curve for n = 5 and explicit in Sigalotti, Hendi and Sharifzadeh’s work, one finds [4]

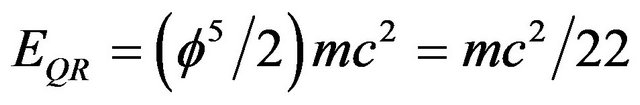(6)

exactly as expected. For an overview see Tables 1 and 2. We mention on passing that for 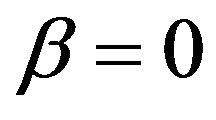we naturally find Newton’s kinetic energy while Einstein’s equation E = mc² is retrieved f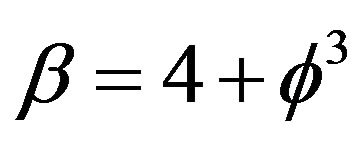or or .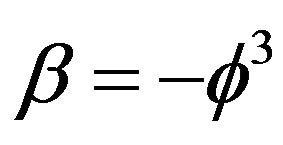

3. Relevance to the Issue of the Missing Dark Energy of the Cosmos

The failure of accurate cosmic measurements to confirm Einstein’s equation’s prediction of the amount of energy in the cosmos presented theoretical physics and cosmology with a serious challenge [7]. At the end scientists were facing two alternatives, namely either Einstein’s equations must be revised or one has to postulate a new unknown force or matter and energy [7]. That is the critical situation under which the hypothesis of missing dark matter or more generally dark energy was introduced [4,7].

The present author noticed before and with considerable satisfaction that 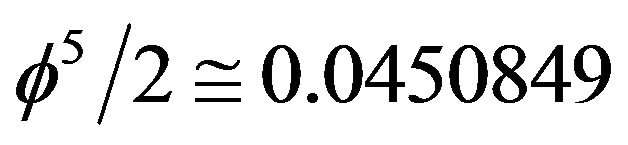makes the energy prediction of the new quantum relativity equation 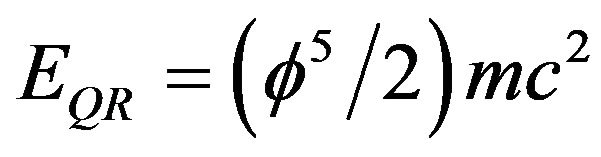a mere 4.508% of the energy prediction of the original Einstein famous energy formula, i.e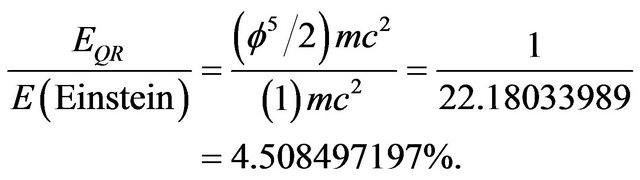. [7]

(7)

This is exactly equal to the measured total ordinary matter and energy in the universe [7] which was the main cause for the conjecture of the as yet hypothetical form of energy (and matter) dubbed dark matter and dark energy and which when taking the above into consideration amounts to the energy of a quantum wave [4,7]

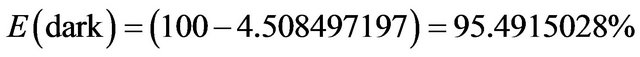(8)

of the total theoretical energy in the universe. Here for convenience we are lumping energy and matter together in E [7].

The above equation alone shows clearly that dark energy is extremely likely to be connected to the fact that Einstein did not include in his derivation the effects of quantum entanglement [4] stemming from the hyperbolic Cantorian fractal geometry of real spacetime as reflected in the topology and geometry of the compactified Klein modular curve [5,6] discussed earlier on in paragraph 2. This of course was not an oversight by Einstein as neither quantum mechanics nor quantum entanglement were known in 1905 when special relativity was conceived. Later on however Einstein was so full of doubt regarding

Table 1. Invariant transformation.

Table 2. The dependence of maximal energy E on spacetime geometry as reflected in the factor.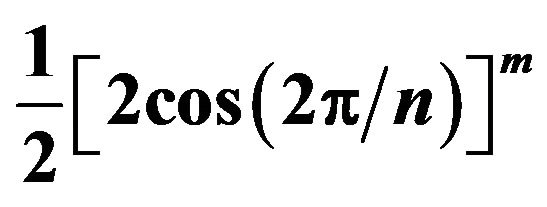

quantum mechanics that it is inconceivable that he would have included it in his theory of relativity. As a result Einstein kept to his purely relativistic formula E = mc² which over estimates the energy by 95.5% and did not consider a quantum relativistic formula like our Equation (6).

In Tables 1 and 2 we summarize our results and give instructive comparisons between the Euclidean and hyperbolic geometry of space as far as it affects the relativistic equations.

4. Discussion

In general we could say that Einstein’s theory of special relativity is based upon 4 dimensional Euclidean spacetime and all the relevant equations may be derived from simple trigonometry of a golden mean proportioned triangle. The famous equation E = mc² could easily be derived in this manner as amply demonstrated by Sigalotti, Hendi and Sharifzadeh [1,2].

In the present work we showed that E = mc² could be elevated from a purely relativistic equation to a quantum relativistic equation 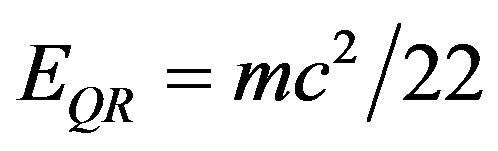which can explain the origins of the hypothetical dark energy believed to make up about 95.5% of all the energy in the cosmos [7]. This modification is obtained by simply changing the classical geometry of a golden mean proportioned traingle to a golden mean hyperbolic triangle. 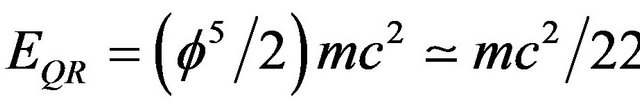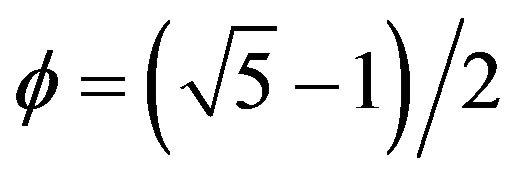This change in geometry is shown to have a deep physical meaning, namely the inclusion of the effect of quantum entanglement in E = mc² and converting it to where and 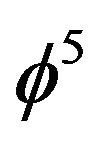is the celebrated Hardy’s probability of quantum entanglement [8,9] while the 22 involved in the approximate solution 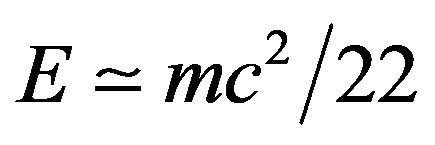may be regarded as the compactified 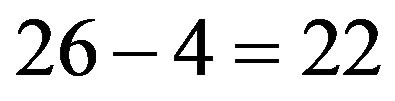dimensions of the bosonic strings of the strong interaction model [4].

5. Conclusion

Sigalotti, Hendi and Sharifzadeh were able to derive all the important results of special relativity and in particular E = mc² from a golden mean proportioned Euclidean triangle [1,2]. In the present work we replace the Euclidean geometry with a hyperbolic golden mean geometry and use the same strategy to derive a corresponding energy equation. This equation turns out to be a quantum version of Einstein’s famous equation but includes the vital quantum mechanical effect of entanglement. In other words, our new energy formula 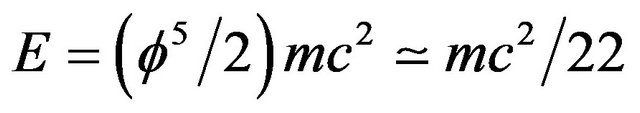is an effective quantum gravity equation which unlike that of the purely relativistic equation of Einstein, predicts the correct amount of energy contained in the universe.

REFERENCES