ABSTRACT

According to the formula of translational motion of vector along an infinitesimal closed curve in gravitational space, this article shows that the space and time both are quantized; the called center singularity of Schwarzschild metric does not exist physically, and Einstein’s theory of gravity is compatible with the traditional quantum theory in essence; the quantized gravitational space is just the spin network which consists of infinite quantized loops linking and intersecting each other, and that whether the particle is in spin eigenstate depends on the translational track of its spin vector in gravitational space.

1. Introduction

The quantization of gravitational space is one of important questions for the world’s physicists in recent decades. String theorists tried to bring Einstein’s theory of gravity and quantum theory into a unified theoretical framework with the method to introduce extra dimensions, but the attempt encountered some real problems. The loop quantum theory of gravity takes the connection rather than the metric as the basic field quantity, hopes for the realization of gravitational space quantization and the unification of Einstein’s theory of gravity and quantum theory with that. But, the metric and connection are not peculiar to gravitational space, any flat or curved space could have own metric and connection, just the specific form is different. Unlike the metric and connection, the curvature is a peculiar physical quantity to curved space besides the artificial curve coordinates embedded in flat space. Could say, the curvature is the core concept of gravitational space. So, the investigation on quantization of gravitational space should perhaps start with studying the relation of the curvature with some measurable physical quantity. We will show the space and time both are quantized via calculation from the formula of translational motion of vector along an infinitesimal closed curve in gravitational space, and Einstein’s theory of gravity is compatible with the traditional quantum theory in essence.

2. The Change of Spin Vector and the Area Enclosed by Closed Curve

According to general relativity, when the vector 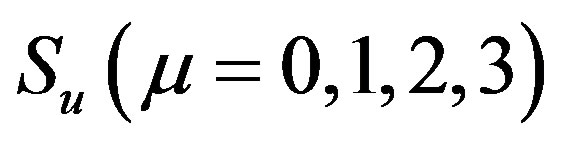has performed a translational motion along an infinitesimal closed curve in gravitational space and gone back to the initial position its change is [1,2]

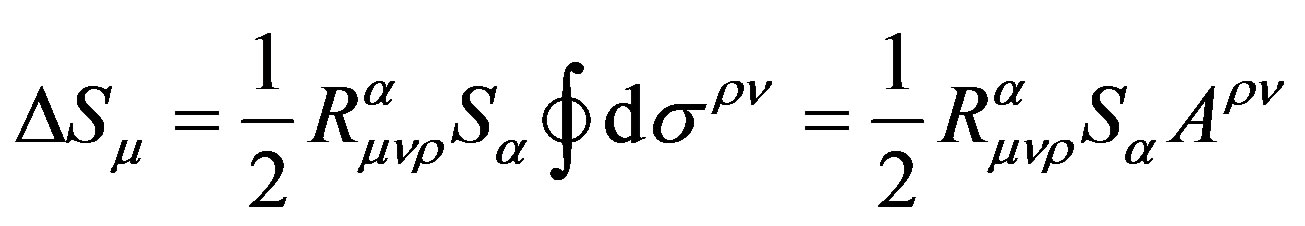, (1)

where

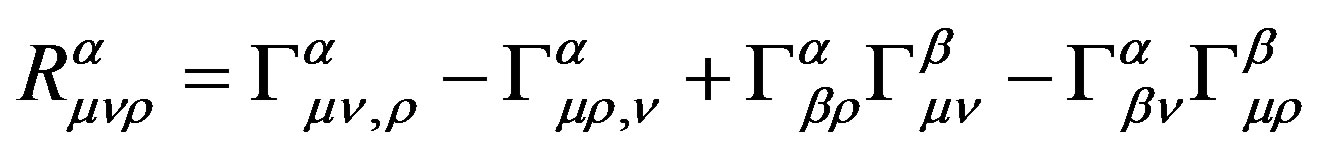(2)

is Riemann-Christophe curvature tensor, and the antisymmetric area tensor

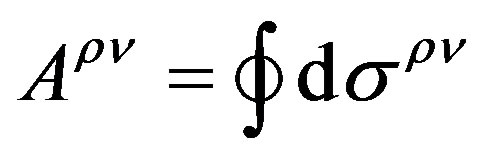(3)

is the projection of the surface enclosed by the infinitesimal closed curve in fourdimensional space-time on the 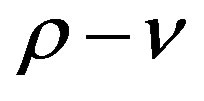coordinate surface, where

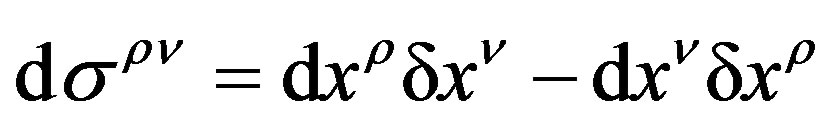(4)

is the antisymmetric area element[3,4].

According to the explanation of general relativity in the literature the Equation (1) shows that the necessarysufficient condition of the vector 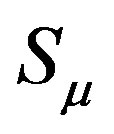does not change is that the curvature tensor equals zero at the point when the vector has translated along an infinitesimal closed curve in gravitational space and gone back to the point 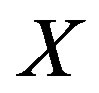[5]. Hence if the change 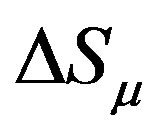of vector and the curvature tensor 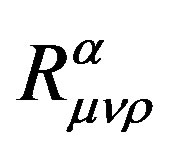are both given at the point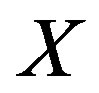, then the area enclosed by the closed curve pass the point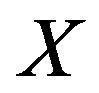could be obtained from Equation (1). It is not difficult to think that the spin is just such a vector. For the most of particles known by now their spin is measurable, but in the gravitational space of Earth, so its change could be determined in principle.

We know that the spin of fermions and bosons is half-integer and integer time of electronic spin respectively, which both could be written into one equation

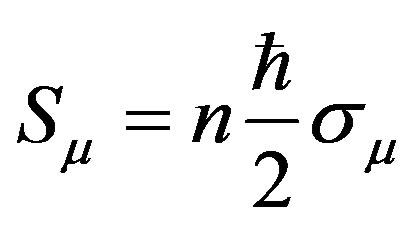, (5)

where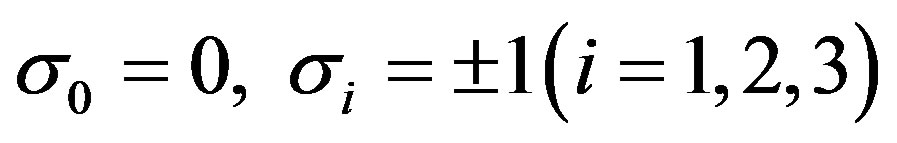. There is 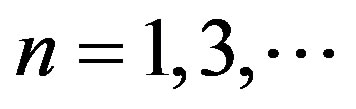for fermions and 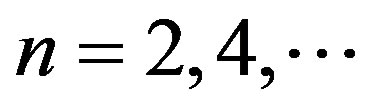for bosons with non-zero spin. Since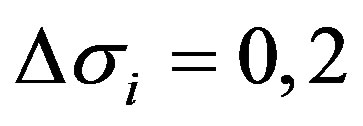, the spin change of particle is

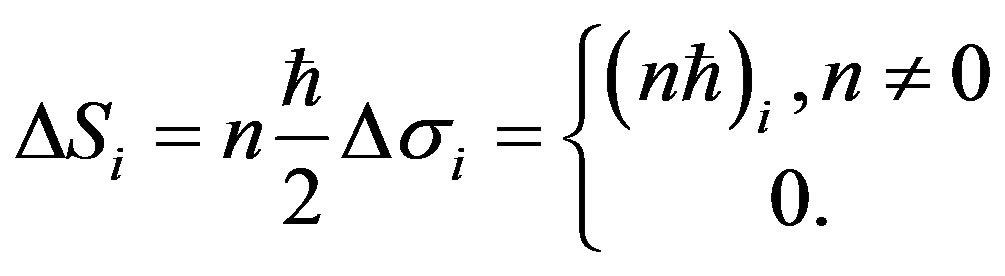(6)

It is self-evident the boson with zero-spin will be not discussed here, because of that the question on spin change does not exist for that particle. We discuss firstly the case of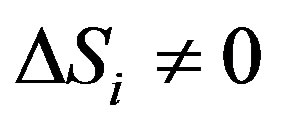, as for the case of 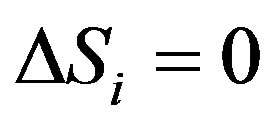will be discussed in the fourth section of this article. For the convenience, imagine a time-orthogonal coordinate system in the static weak gravitational field, i.e. 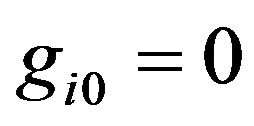, 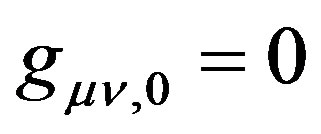and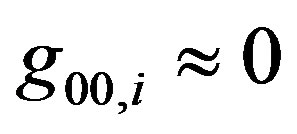, using the relation

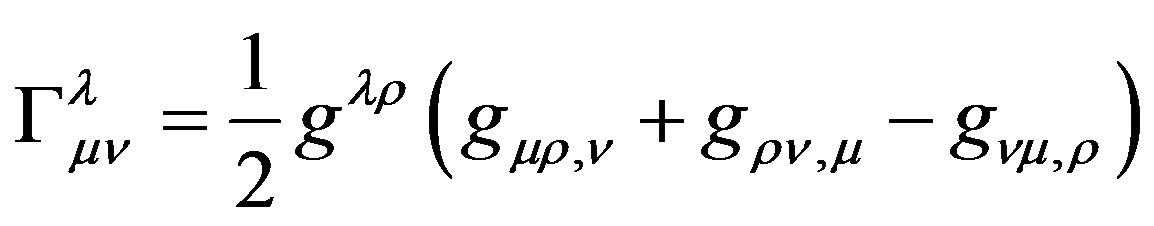(7)

we obtain

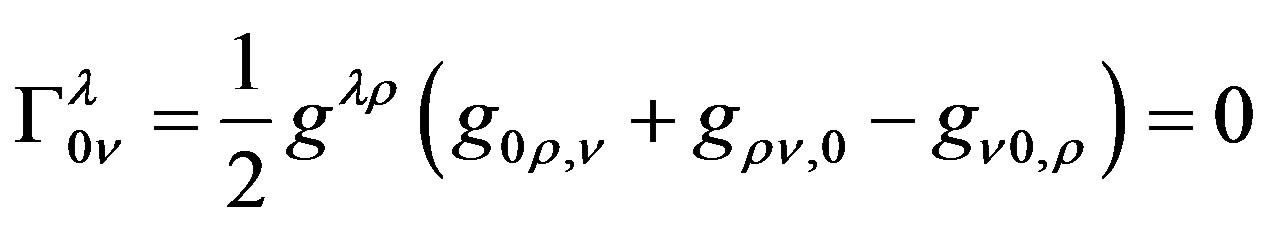then

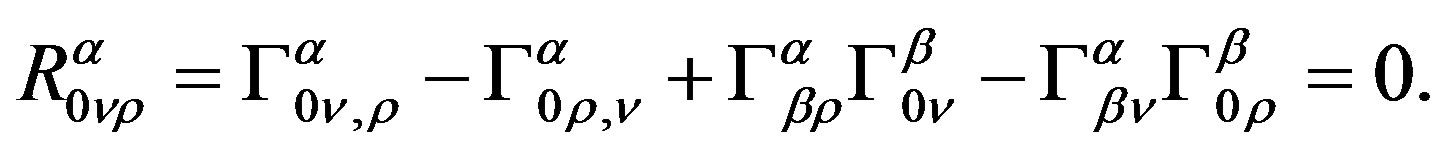
Since the curvature 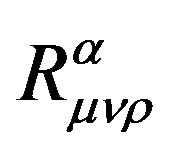is symmetric for front and latter two pairs of indexes but anti-symmetric for each pair of indexes, those curvatures related to time are all zero in Equation (1). So Equation (1) is simplified as

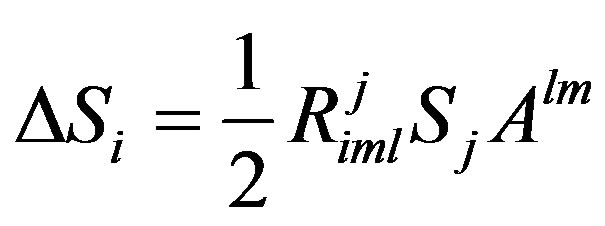. (8)

Substituting 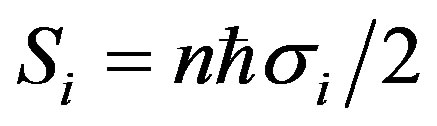and 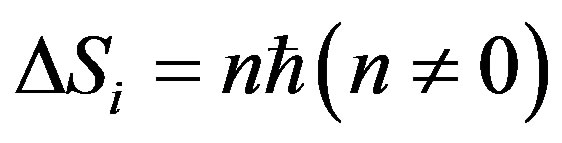into above equation, that is

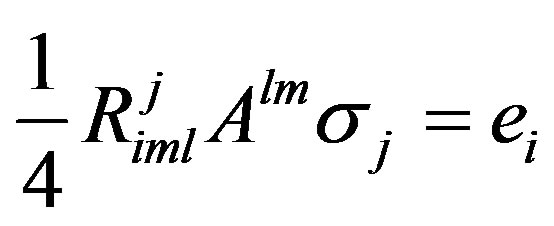, (9)

where 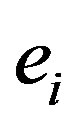is the unit vector in 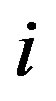direction. Notice 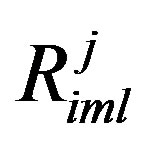is antisymmetric for the front or after pair of indexes, and 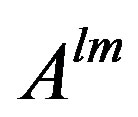is such, too, Equation (9) could be written as

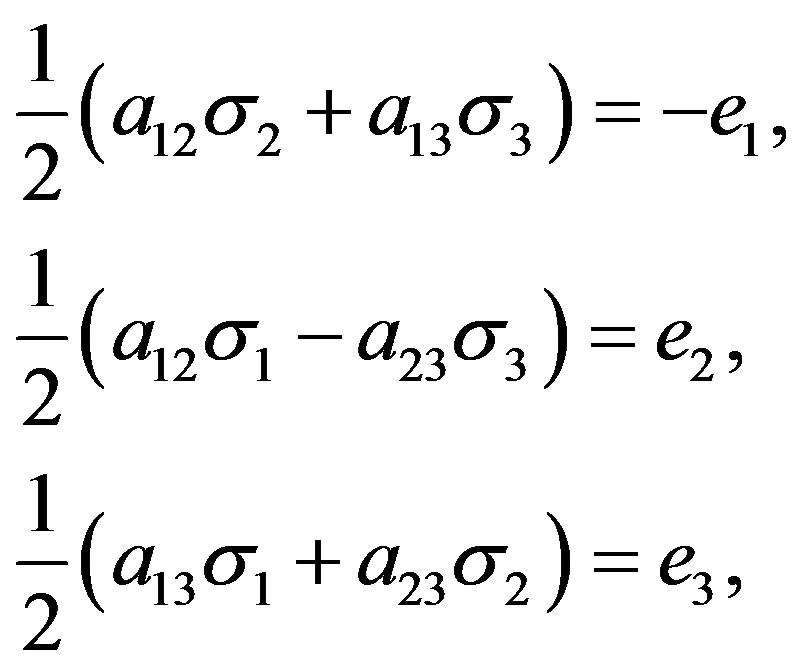(10)

where

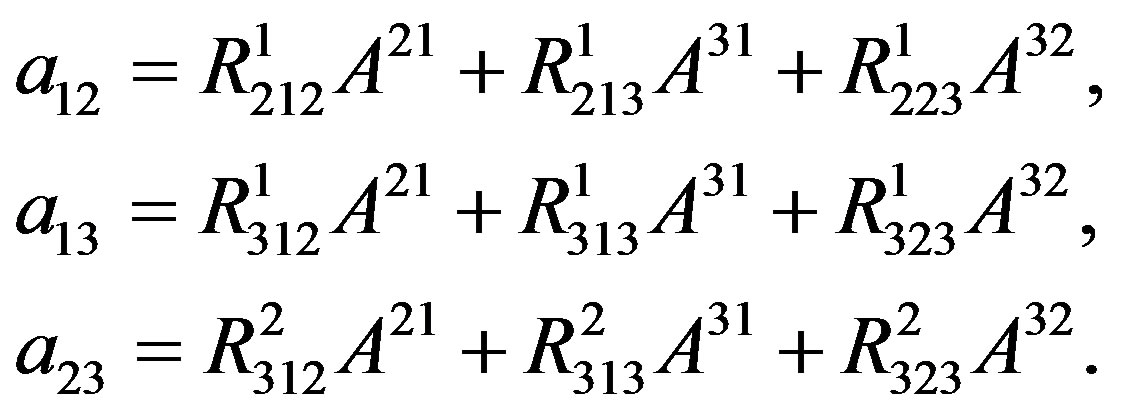(11)

Clearly, equation (10) is a group of linear equations for three unknown 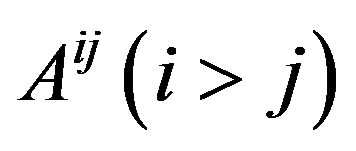when the curvatures and spin operators are given, the 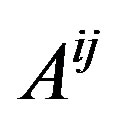should be the linear function of spin operators 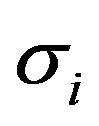and also an operator. Hence the 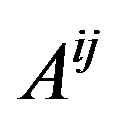is anti-commutative to each other same as the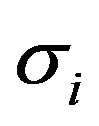. Squaring and then extracting each equation in Equation (10), which could be rewritten into the following matrix equation:

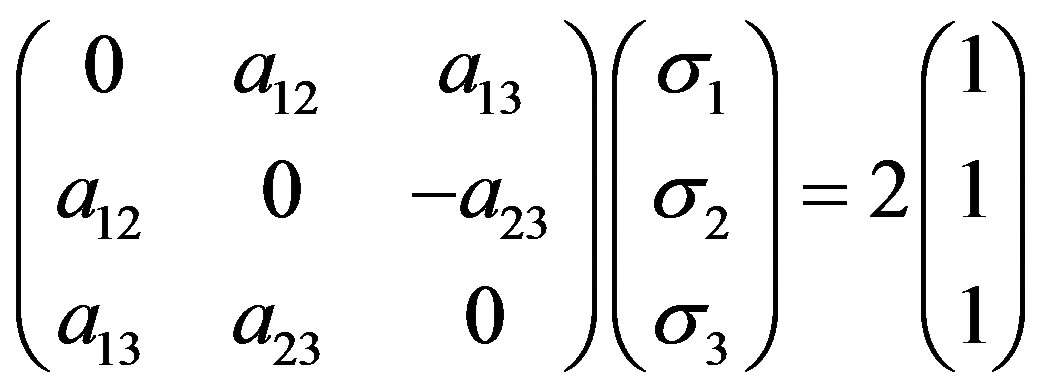. (12)

Because the right side of above equation does not equal zero, the determinant of coefficient matrix in the left side does not, too:

.

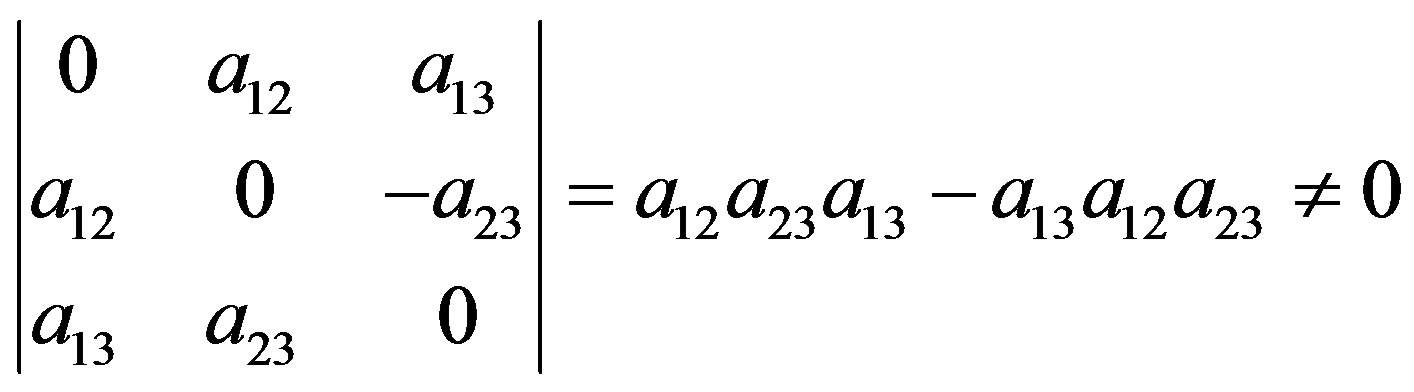Thus 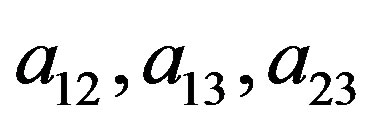are all not zero; otherwise, the equation above is not established. So the solution of Equation (11) according to Cramer formula is

(13)

where

.

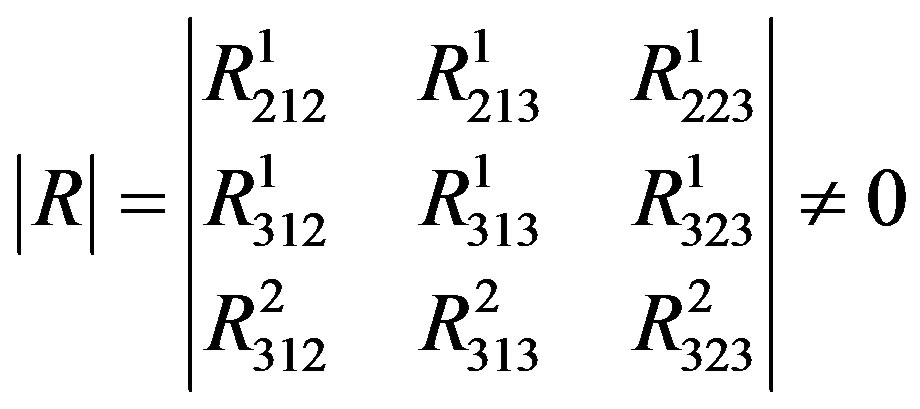The Equation (13) shows the projection of surface enclosed by the closed curve of translational motion of spin does not equal zero on every coordinate surface in third-dimensional space, namely the surface does not equal zero. This implies that the gravitational space is quantized. Next we will solve Equation (1) in the static sphere-symmetric metric—Schwarzschild external metric in order to verify concretely this conclusion and show the time is quantized, too. As said previously, we discuss firstly the case of 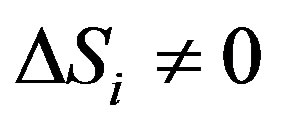and then the case of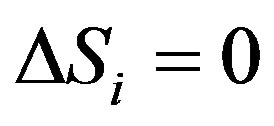. In fact, the spin change could be zero only in one direction in the latter case.

3. The Case in Which the Change of Spin Is Not Zero in Every Direction

We know that Schwarzschild metric is

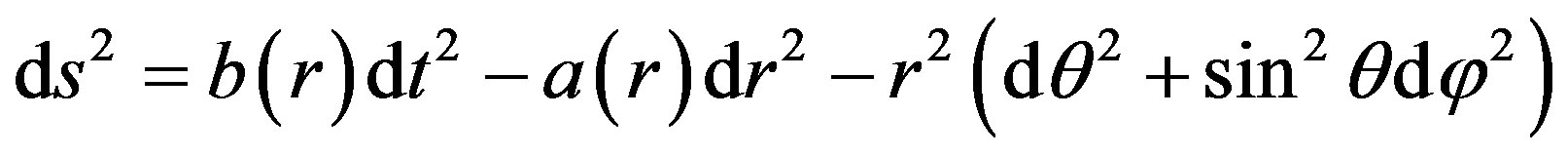where light speed and the metric tensor is

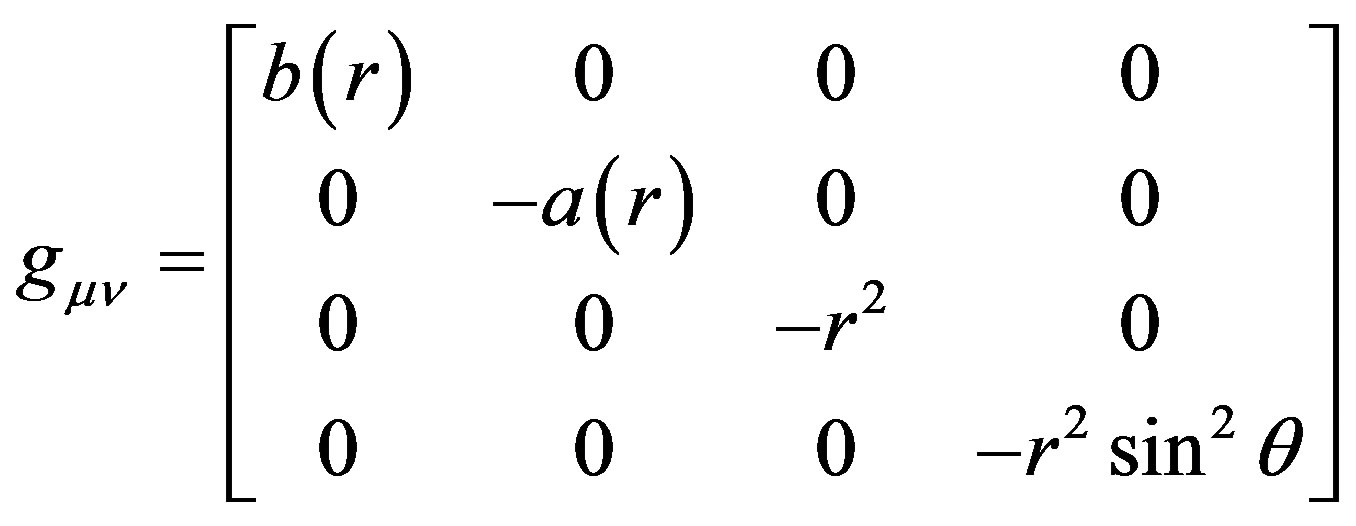, (14)

where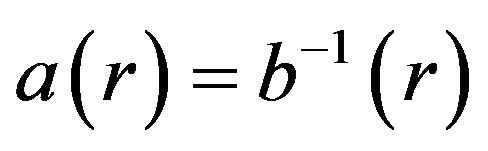, 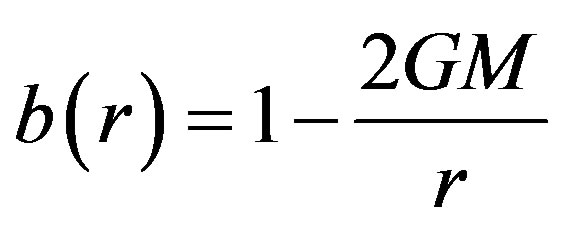[6].

From Equation (14) we obtain the following nonzero connection components using Equation (7):

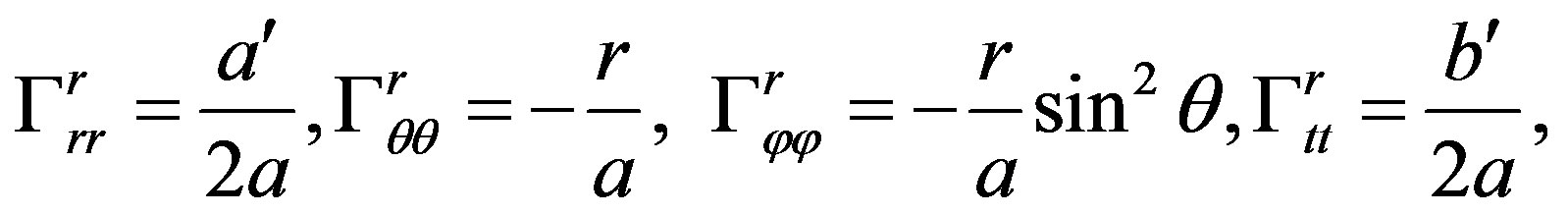
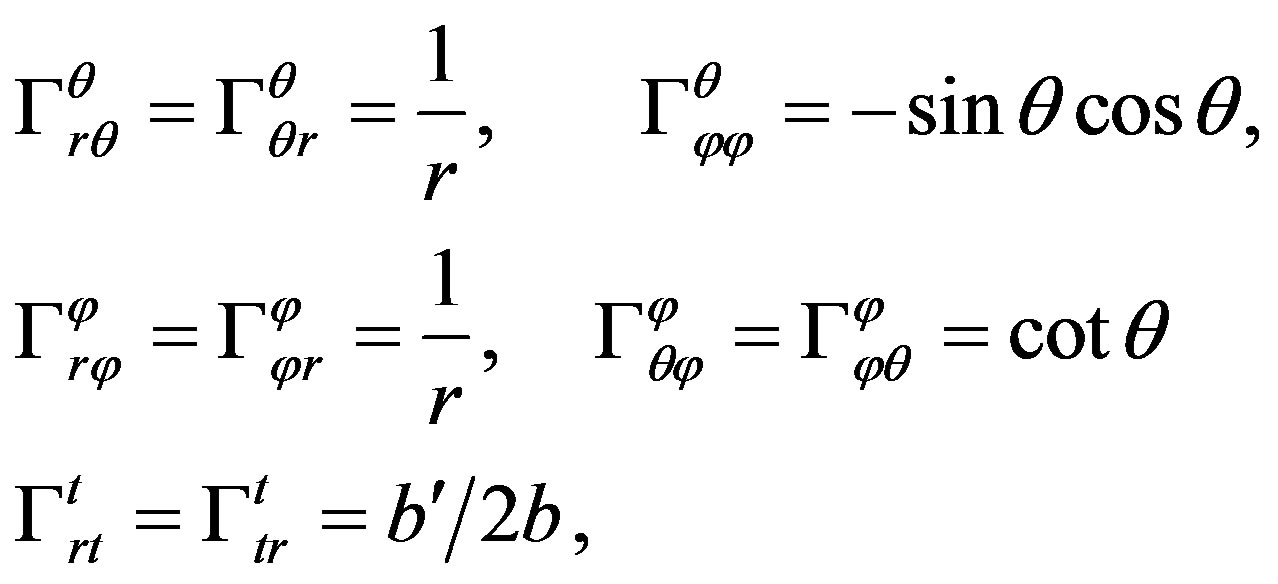(15)

where 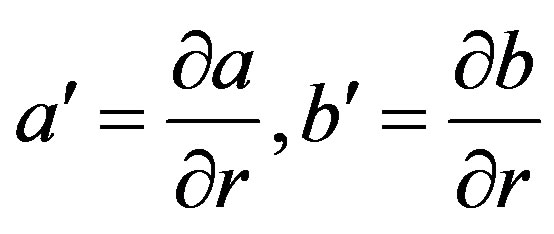[6]. So we have

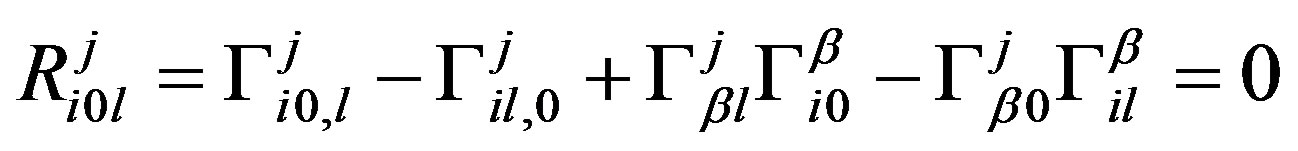, (16)

thereby we obtain similarly Equation (9) for the same reason as said previously after 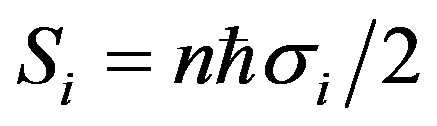and 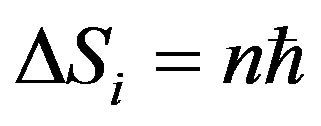(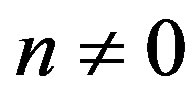) are substituted into Equation (1):

, (17)

where

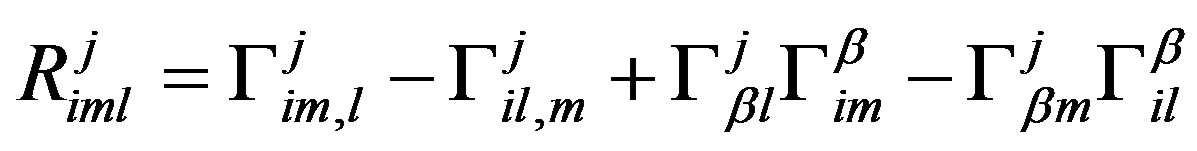. (18)

Notice 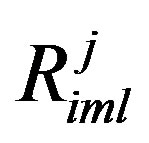and 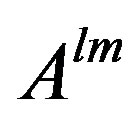are both antisymmetric for indexes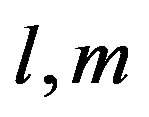, Equation (17) could be written as

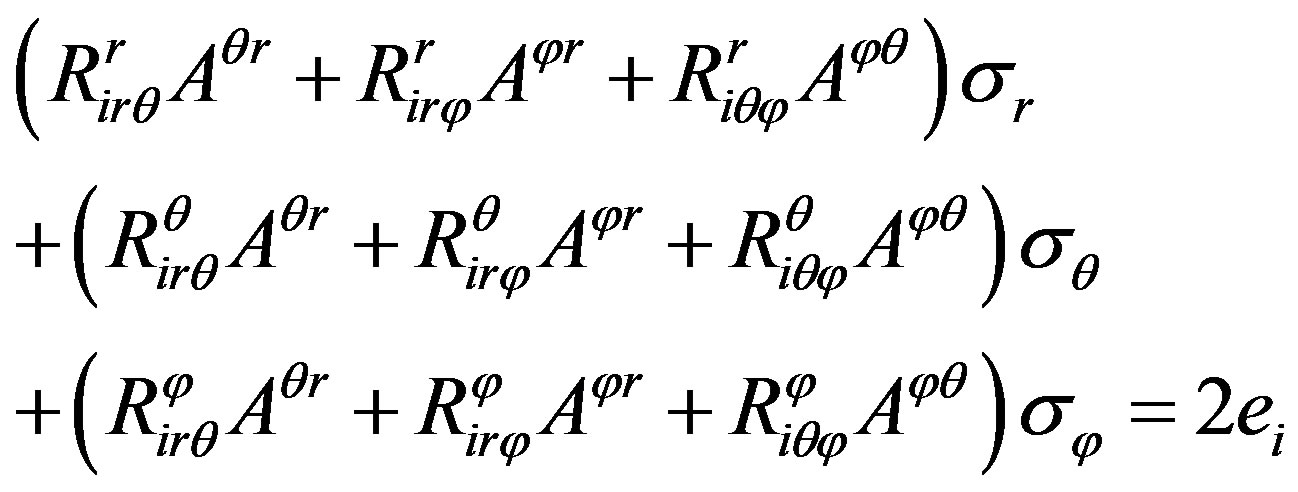(19).

Because 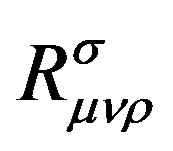is antisymmetric for the two front indexes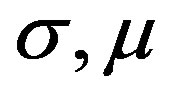, those curvatures are all zero in the first brackets on the left side of above equation when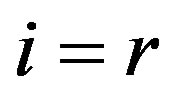, so there is

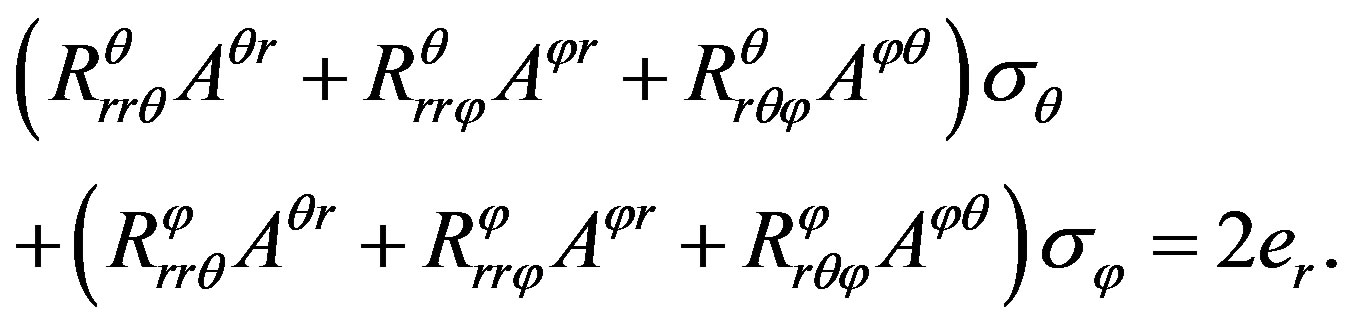(20)

From Equations (15) and (18) we obtain

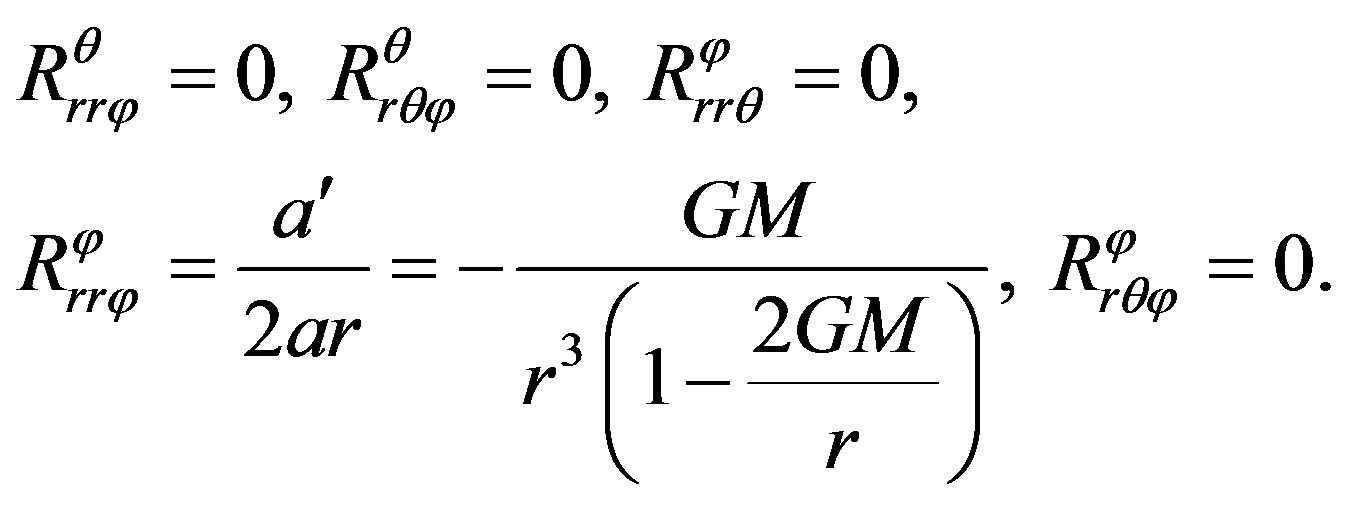
So there are

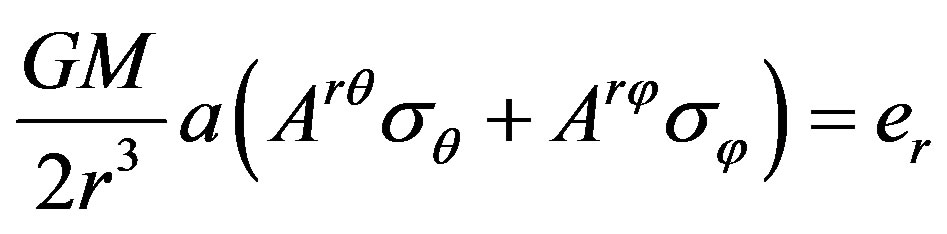, (21)

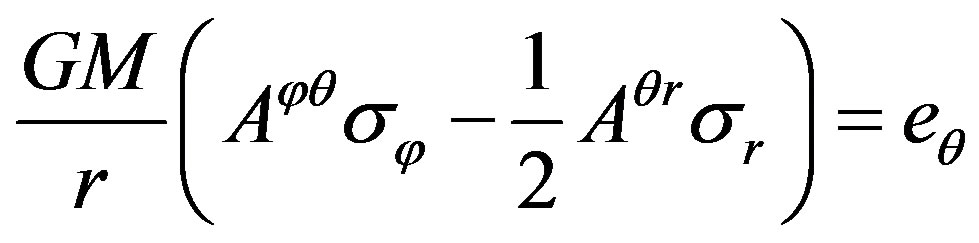, (22)

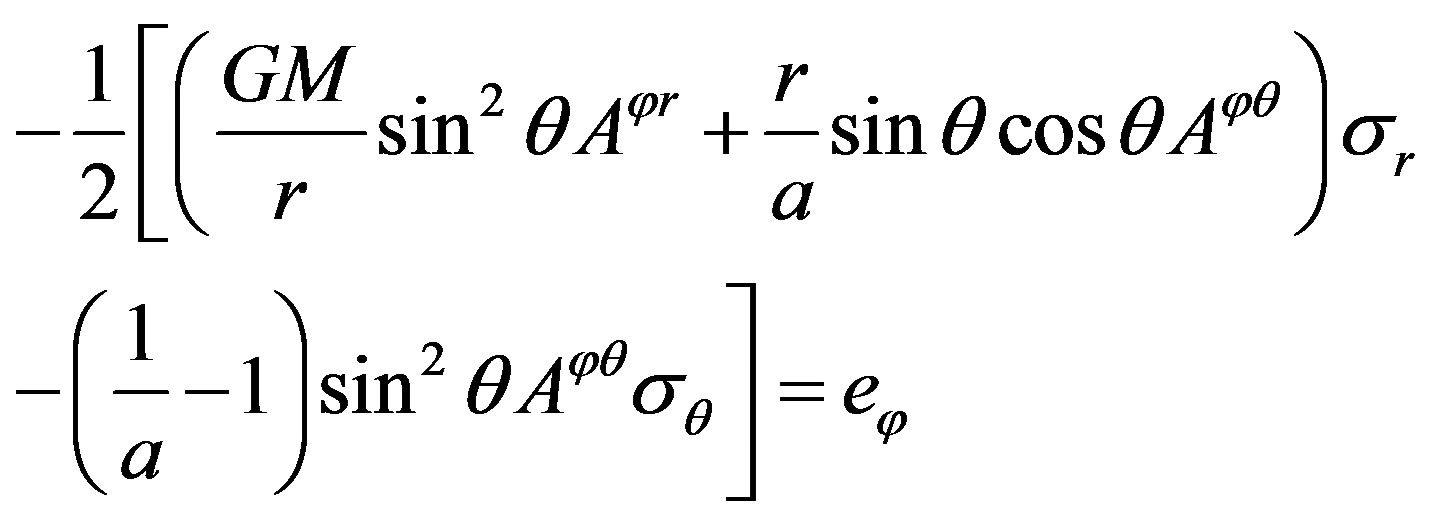(23)

for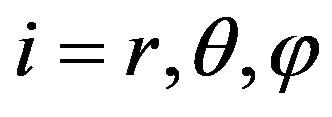, respectively.

We know that a local inertial system could be set at one point in gravitational space according to general relativity. So, set a spherical coordinates with the point 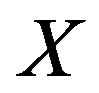as the origin and make its three coordinates parallel with the three coordinates of Schwarzschild metric, respectively, and then substitute the radius distance in the inertial system for the radius distance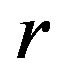. Since Schwarzschild metric is sphere-symmetric, take 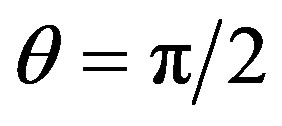and 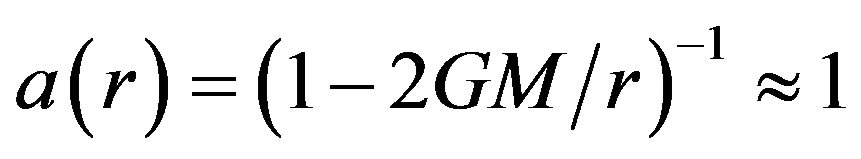for weak field in equation (23). 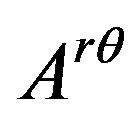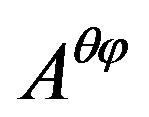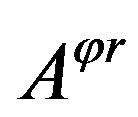Notice the repeated indexes no longer indicate summation in above three equations, and, and are anti-commutative to each other same as the Pauli operators, squaring and then extracting each equation above we have

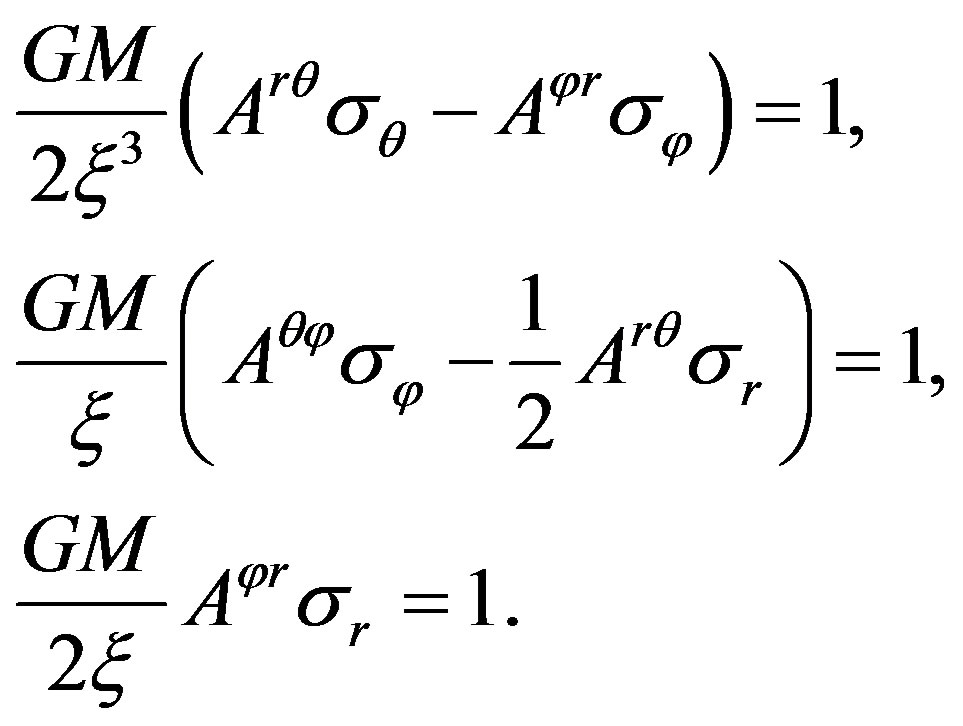(24)

These equations could be rewritten into the following matrix equation:

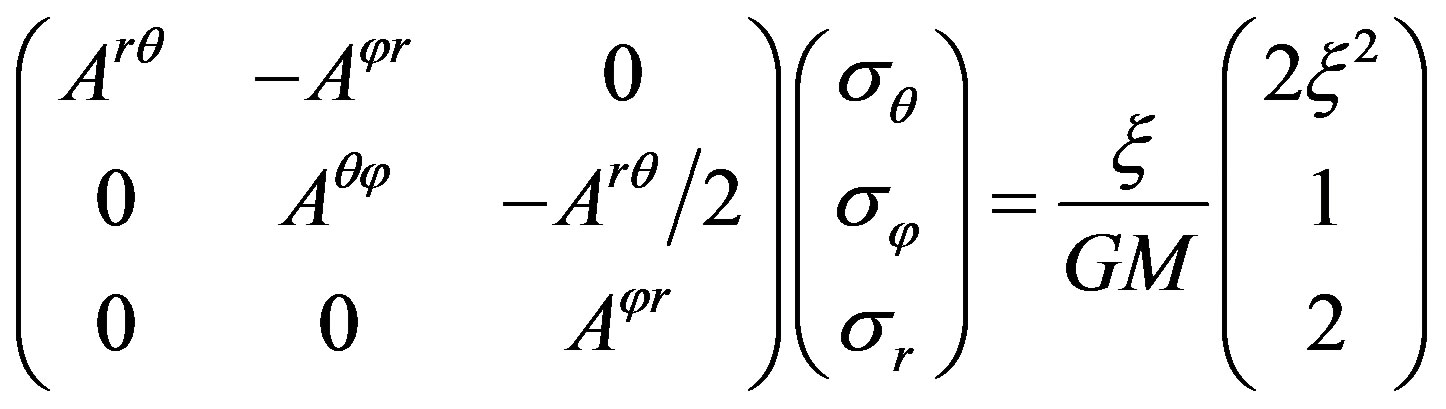. (25)

Because the right side of above equation does not equal zero, the determinant of coefficient matrix in the left side does not, too:

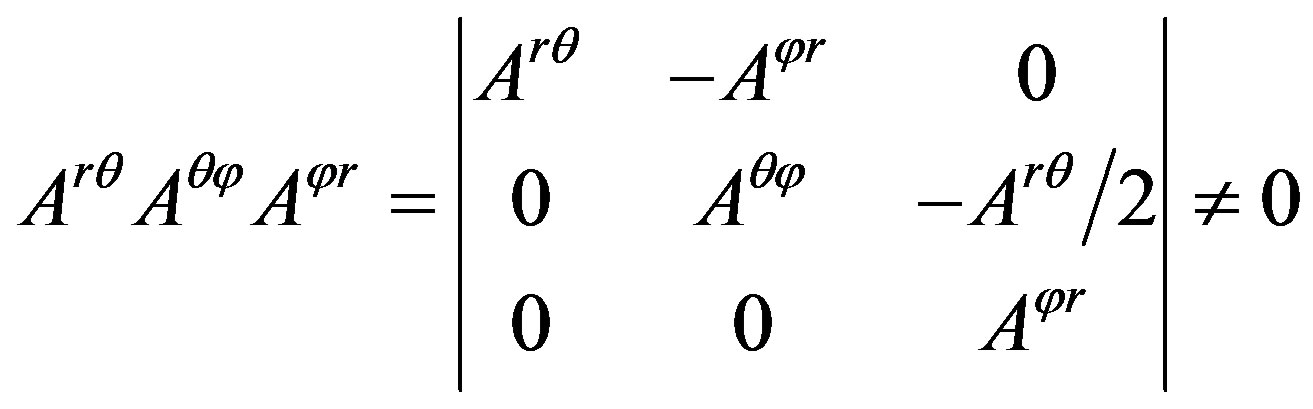. (26)

This shows that the projection of the surface enclosed by the closed curve of translational motion of spin does not equal zero on every coordinate surface in third-dimensional space, namely the surface is not zero.

From Equation (24) we obtain using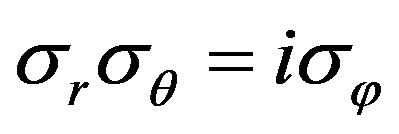, , 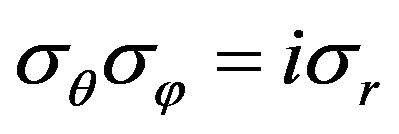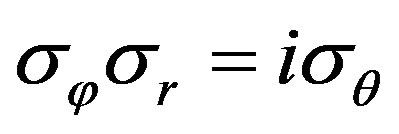and

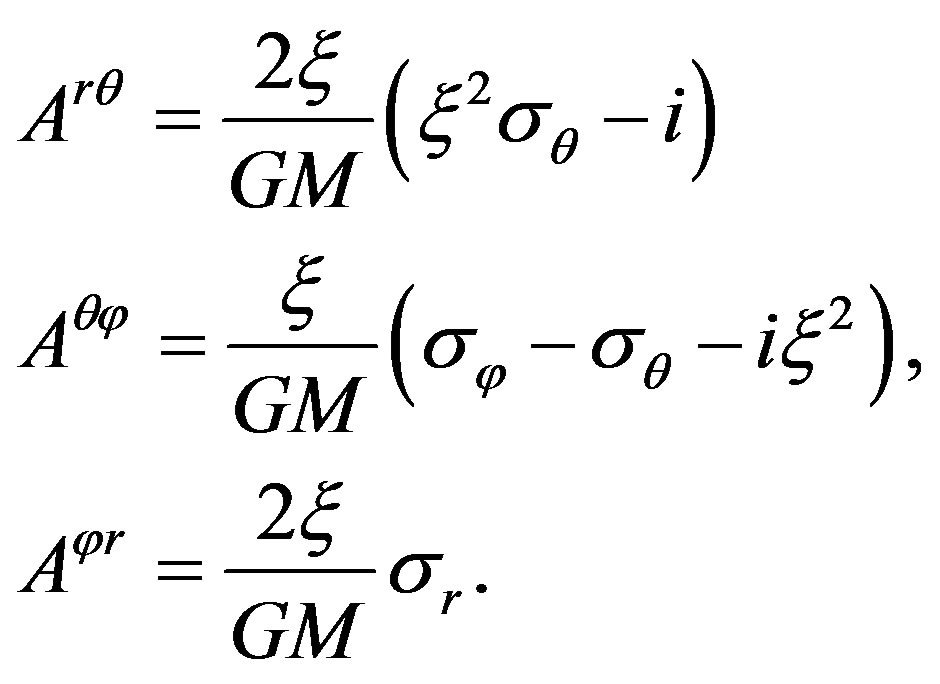(27)

This shows that the area tensor is the linear function of spin operators 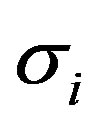and also an operator, as said previously. Neglecting the terms of imaginary number in above equation in order to ensure that the area is real we obtain

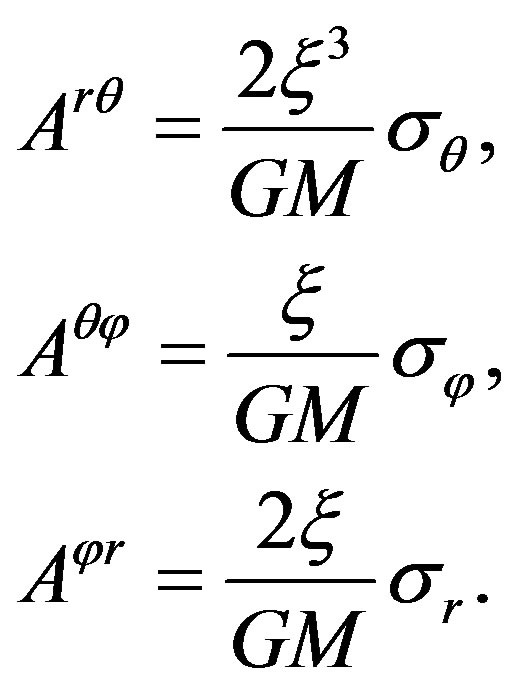(28)

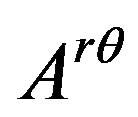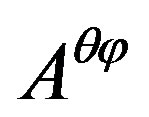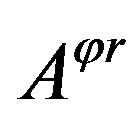Obviously, as said previously, , andare anti-commutative to each other. Notice the eigenvalue of 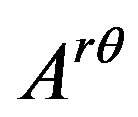has the dimension of area and the eigenvalues of 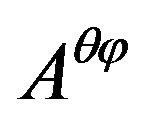and 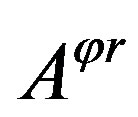without dimension are in the ratio 1:2 we see that the surface enclosed by the closed curve is an infinitesimal parallelogram in the plane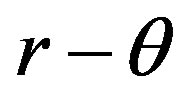, its length and width are in the ratio 2:1, and its area 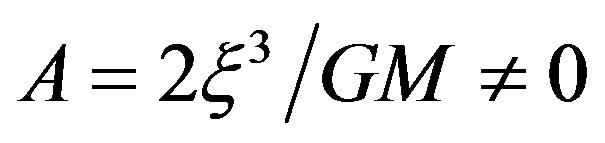. In addition, Equation (28) shows that two area vectors equal in magnitude and opposite in direction are two eigenvalues of the area tensor operator, this is consistent with that the spin operator has two eigenvalues opposite in direction.

Therefore we might as well call these closed curves the quantum loop or Wilson loop according to the discussion above. In this sense the gravitational space is just the often-mentioned spin network, which consists of infinite quantized loops that link and intersect each other [7-15], because the point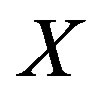to say here is an arbitrary point in gravitational space. It is more important the results above imply that Einstein gravitational theory is compatible with the traditional quantum theory in essence, such is in the case of static weak field at least.

In fact, if we write the two sides of the parallelogram as

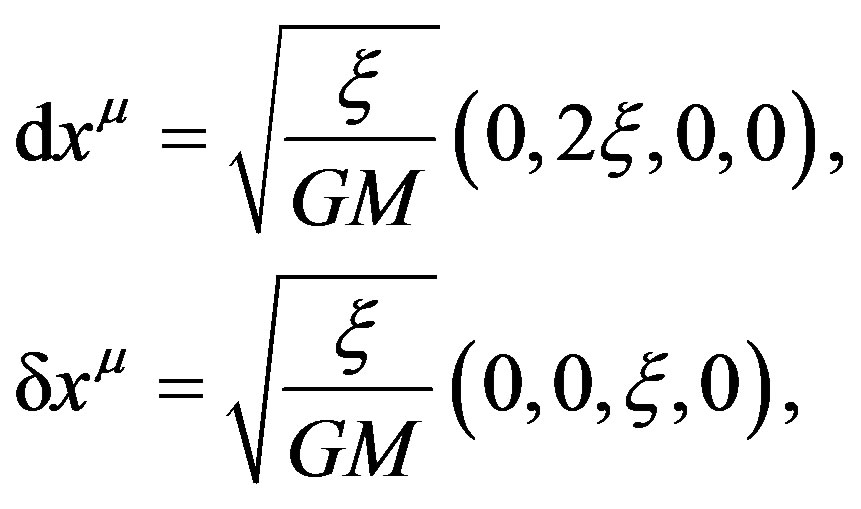(29)

and substitute them into Equation (4) we could obtain 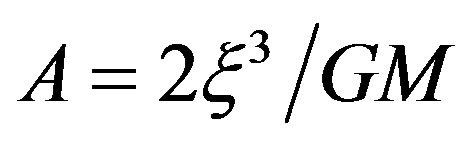immediately.

The reason why the smallness parallelogram is in the plane 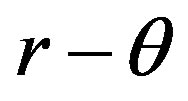is that Schwarzschild metric is a static sphere-symmetric,where the direction of gravity is radial. Thus the moment of gravity on the rigid smallness parallelogram equals zero, namely the particle is in the steady vibration state or known as quantum fluctuation state. Notice the side length of the parallelogram is not zero (refer to Equation (26)), the length 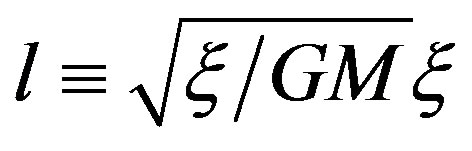should satisfy the following condition on standing wave:

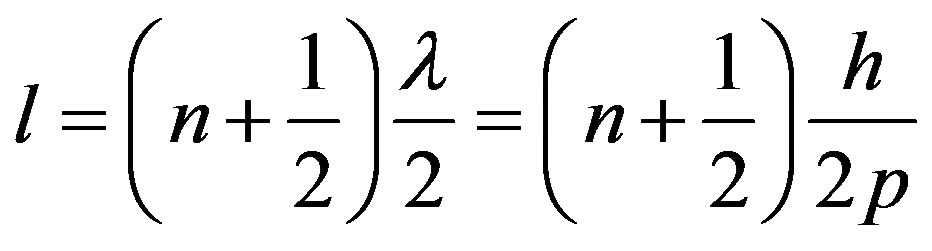, (30)

where 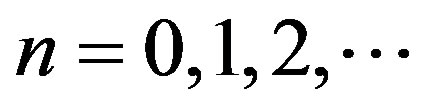is called the quantum fluctuation number, and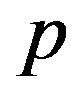is momentum of particle. Since the energy is relative, the energy of particle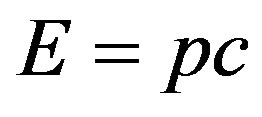, so

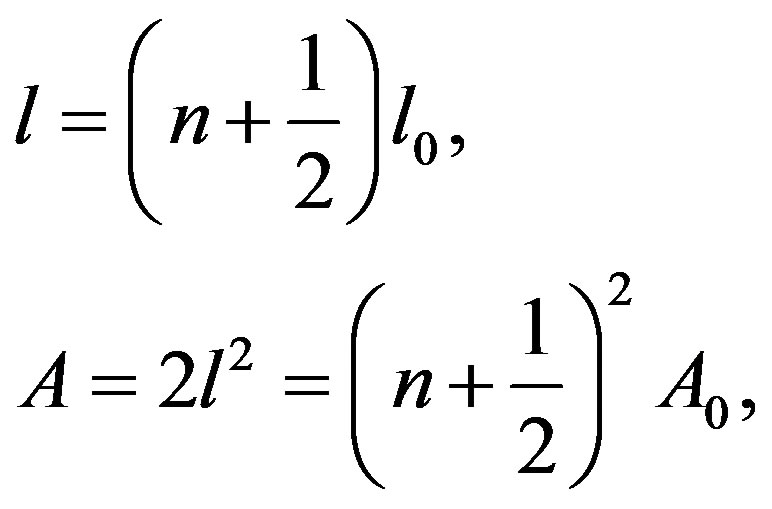(31)

and the time could be defined as

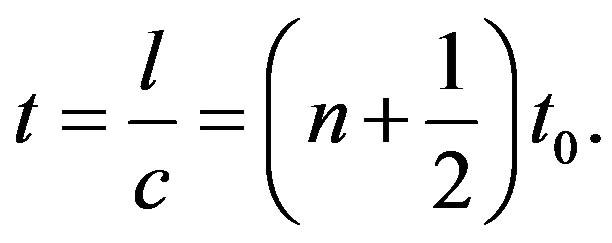(32)

These equations above show the space and time both are quantized, where

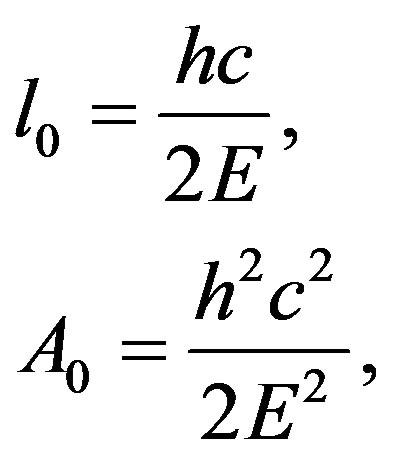(33)

and

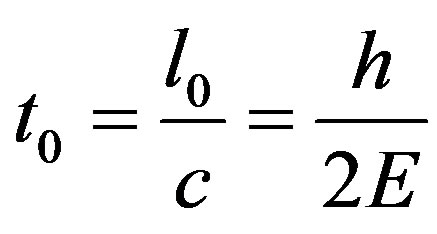(34)

is called the length quantum, the area quantum and the time quantum, respectively.

The results above show that the space or time quantum is related to the energy of particle, but the space or time quantum has the lower limit as long as the energy of particle has the upper limit. In fact, it is meaningless to talk about the space-time out of the material, let alone the quantization of space-time. From the several equations above we see that the space and time both do not equal zero even if the quantum number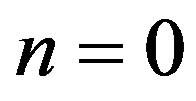, namely the called center singularity of Schwarzschild metric does not exist physically, because its existence implies the space-time is continuous. In other words, Einstein’s theory of gravitation is compatible with the traditional quantum theory in essence, such is in static weak field at least. For instance, if the energy of particle equals the Planck energy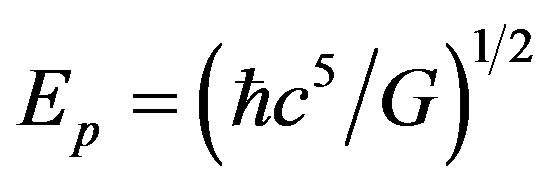, then

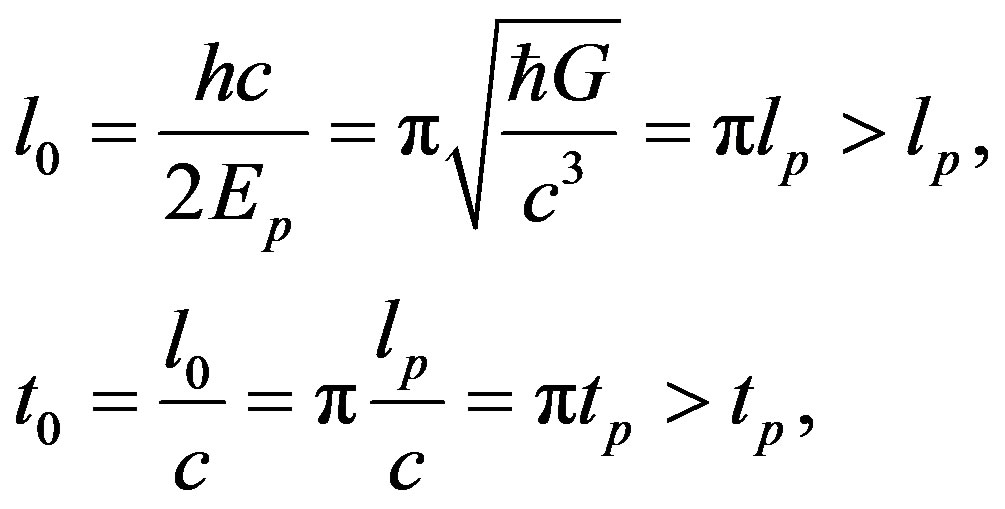(35)

where the Planck length 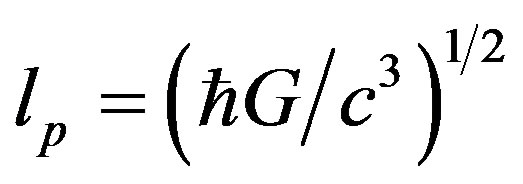and the Planck time.

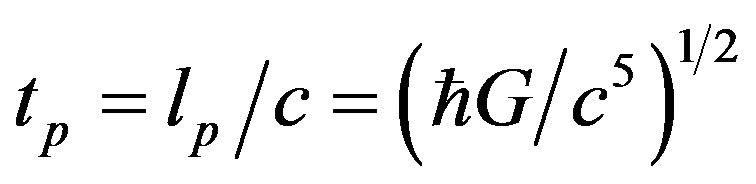4. The Case in Which There Is Zero-Change of Spin Only in One Direction

There 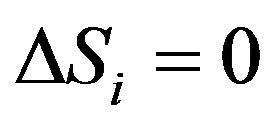means that the particle is in the eigenstate of spin operator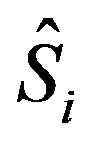. Since the three operators 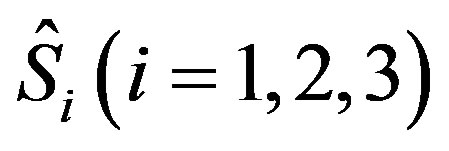are anti-commutable to each other, the spin change is impossibly zero in other two directions when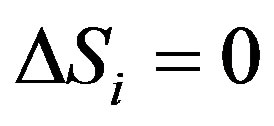. The following three situations are discussed next.

If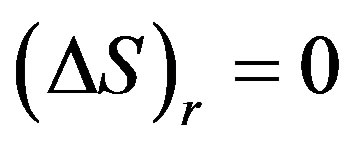, we could obtain the following equations formally similar to Equation (24) from Equation (19):

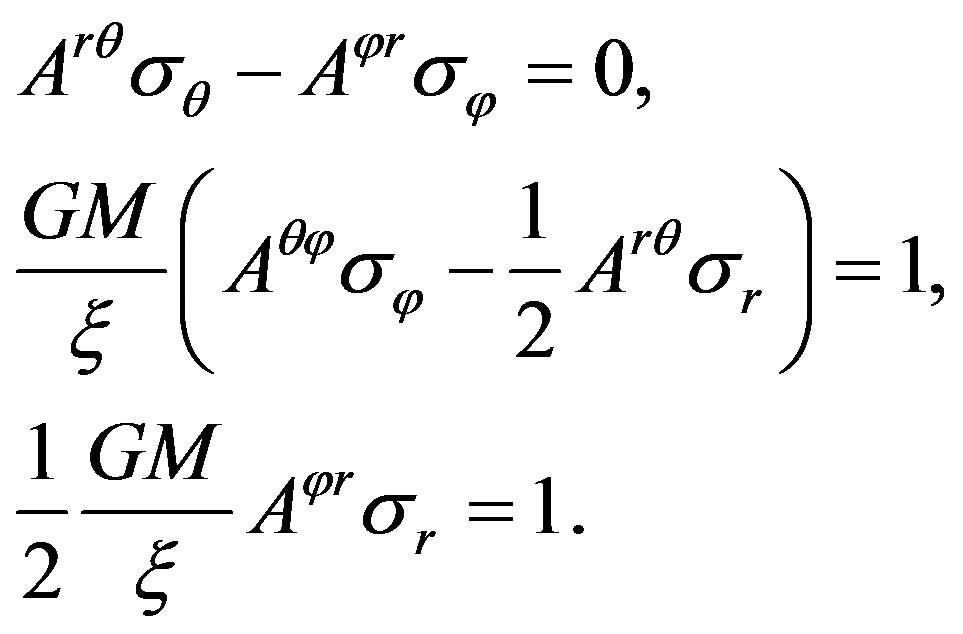(36)

Imitating the method from Equation (24) to Equation (28) we obtain

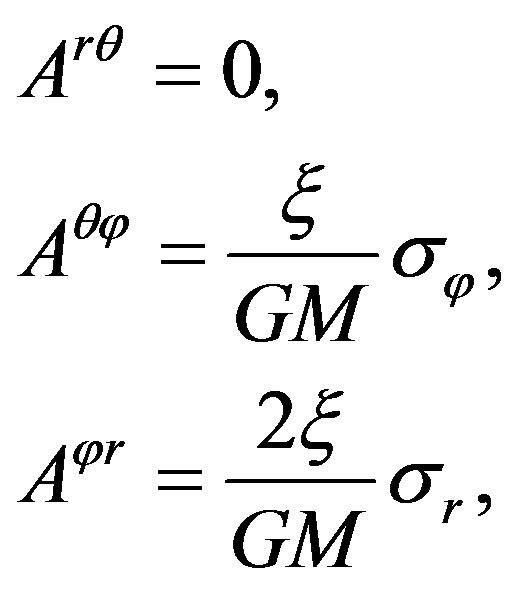(37)

This shows that the spin vector doesn’t move, the socalled area equals zero naturally.

If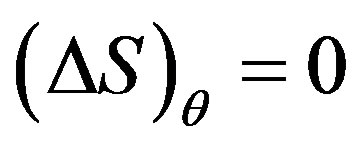, then there are

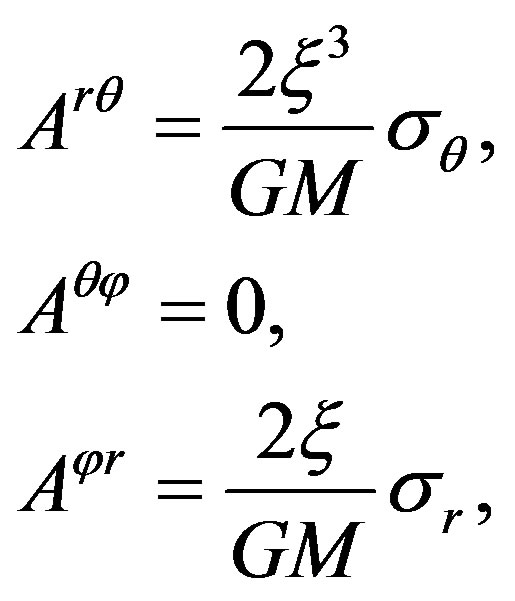(38)

this shows that the translational track of the spin vector is one of long sides of the infinitesimal parallelogram rather than the complete parallelogram.

If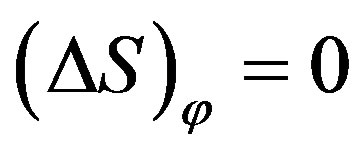, then there are

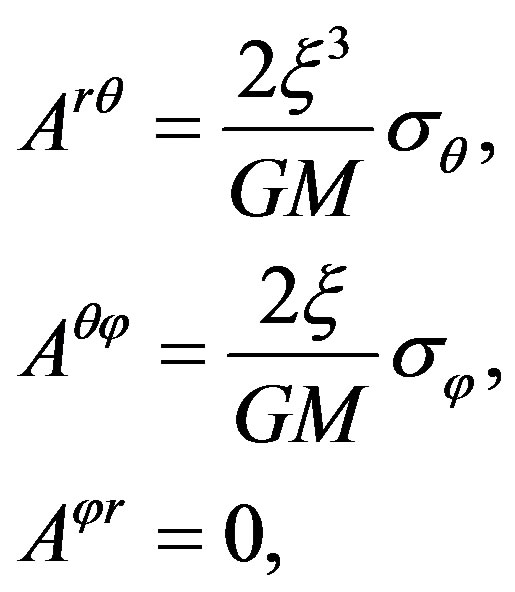(39)

this shows that the translational track of the spin vector is one of short sides of the infinitesimal parallelogram.

Therefore that whether the particle is in spin eigenstate depends on the infinitesimal translational track of its spin vector in gravitational space. The particle is in spin eigenstate if the translational track is zero or an infinitesimal straight line; otherwise, the particle is not in spin eigenstate if the translational track is a curve, specially a closed curve.

5. Conclusion

Summary of the discussion above, our conclusion is that the surface enclosed by closed curve of translational motion of spin vector is not zero, and the space and time both are quantized; the called center singularity of Schwarzschild metric does not exist physically, and Einstein’s theory of gravitation is compatible to the traditional quantum theory in essence, such is in static weak field at least; the quantized gravitational space is just the spin network which consists of infinite quantized loops linking and intersecting each other, and that whether the particle is in spin eigenstate depends on the translational track of its spin vector in gravitational space.

REFERENCES