Applied Mathematics
Vol.07 No.16(2016), Article ID:71677,45 pages
10.4236/am.2016.716165
Rate Constitutive Theories of Orders n and 1n for Internal Polar Non-Classical Thermofluids without Memory
Karan S. Surana1, Stephen W. Long1, J. N. Reddy2
1Department of Mechanical Engineering, University of Kansas, Lawrence, USA
2Department of Mechanical Engineering, Texas A & M University, College Station, USA

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: August 10, 2016; Accepted: October 28, 2016; Published: October 31, 2016
ABSTRACT
In recent papers, Surana et al. presented internal polar non-classical Continuum theory in which velocity gradient tensor in its entirety was incorporated in the conservation and balance laws. Thus, this theory incorporated symmetric part of the velocity gradient tensor (as done in classical theories) as well as skew symmetric part representing varying internal rotation rates between material points which when resisted by deforming continua result in dissipation (and/or storage) of mechanical work. This physics referred as internal polar physics is neglected in classical continuum theories but can be quite significant for some materials. In another recent paper Surana et al. presented ordered rate constitutive theories for internal polar non-classical fluent continua without memory derived using deviatoric Cauchy stress tensor and conjugate strain rate tensors of up to orders n and Cauchy moment tensor and its conjugate symmetric part of the first convected derivative of the rotation gradient tensor. In this constitutive theory higher order convected derivatives of the symmetric part of the rotation gradient tensor are assumed not to contribute to dissipation. Secondly, the skew symmetric part of the velocity gradient tensor is used as rotation rates to determine rate of rotation gradient tensor. This is an approximation to true convected time derivatives of the rotation gradient tensor. The resulting constitutive theory: (1) is incomplete as it neglects the second and higher order convected time derivatives of the symmetric part of the rotation gradient tensor; (2) first convected derivative of the symmetric part of the rotation gradient tensor as used by Surana et al. is only approximate; (3) has inconsistent treatment of dissipation due to Cauchy moment tensor when compared with the dissipation mechanism due to deviatoric part of symmetric Cauchy stress tensor in which convected time derivatives of up to order n are considered in the theory. The purpose of this paper is to present ordered rate constitutive theories for deviatoric Cauchy strain tensor, moment tensor and heat vector for thermofluids without memory in which convected time derivatives of strain tensors up to order n are conjugate with the Cauchy stress tensor and the convected time derivatives of the symmetric part of the rotation gradient tensor up to orders 1n are conjugate with the moment tensor. Conservation and balance laws are used to determine the choice of dependent variables in the constitutive theories: Helmholtz free energy density Φ, entropy density η, Cauchy stress tensor, moment tensor and heat vector. Stress tensor is decomposed into symmetric and skew symmetric parts and the symmetric part of the stress tensor and the moment tensor are further decomposed into equilibrium and deviatoric tensors. It is established through conjugate pairs in entropy inequality that the constitutive theories only need to be derived for symmetric stress tensor, moment tensor and heat vector. Density in the current configuration, convected time derivatives of the strain tensor up to order n, convected time derivatives of the symmetric part of the rotation gradient tensor up to orders 1n, temperature gradient tensor and temperature are considered as argument tensors of all dependent variables in the constitutive theories based on entropy inequality and principle of equipresence. The constitutive theories are derived in contravariant and covariant bases as well as using Jaumann rates. The nth and 1nth order rate constitutive theories for internal polar non-classical thermofluids without memory are specialized for n = 1 and 1n = 1 to demonstrate fundamental differences in the constitutive theories presented here and those used presently for classical thermofluids without memory and those published by Surana et al. for internal polar non-classical incompressible thermofluids.
Keywords:
Rate Constitutive Theories, Non-Classical Thermofluids, Without Memory, Convected Time Derivatives, Internal Rotation Gradient Tensor, Generators and Invariants, Cauchy Moment Tensor

1. Introduction
Conservation and balance laws: conservation of mass, balance of linear momenta, balance of angular momenta, balance of moments of moments (or couples), first law of thermodynamics (energy equation) and second law of thermodynamics (entropy inequality) for internal polar non-classical fluent continua were presented in references [1] [2] . A summary of these was also presented in reference [3] in which Surana et al. also presented constitutive theories for internal polar non-classical thermofluids without memory that incorporated convected time derivatives of strain tensor up to order n, density, rate of the symmetric part of the rotation gradient tensor, temperature gradient tensor and temperature as argument tensors of the dependent variables in the constitutive theories at the onset of the derivation. In references [1] [2] [3] comprehensive literature was presented regarding various aspects of non-classical theories that were pertinent in context with internal polar non-classical continuum theory used here for fluent continua. For the sake of brevity these are not repeated here instead interested readers can see references [1] [2] [3] .
Another significant discussion in references [1] [2] [3] is the discussion of mathematical description for fluent continua. It was established that in fluent continua one monitors the state of the matter at fixed locations, hence mathematical models describing such processes do not contain information regarding displacements therefore these descriptions can neither be Lagrangian nor Eulerian. Nonetheless since the fixed locations are occupied by different material particles during evolution, the fixed location can be viewed as current positions of some material particle during evolution. This thinking persuades one to believe that the mathematical descriptions used for fluent continua are Eulerian descriptions. This thinking is not contested in this paper, but is rather used as this approach is what is used for mathematical descriptions of fluent continua.
The notations used in this paper have been used by the authors in the current literature, nonetheless some description and their use in deriving conservation and balance laws are presented in the following. Over bar is used on quantities to express quantities in the current configuration in Eulerian description, that is, all quantities with over bars are functions of current coordinates  and time t.
and time t. 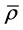 is the density of the fluid in the current configuration and is a function of
is the density of the fluid in the current configuration and is a function of  and
and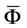 ,
, 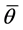 , and
, and 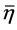 denote the Helmholtz free-energy density, temperature, and entropy density, respectively in the current configuration and are also functions of
denote the Helmholtz free-energy density, temperature, and entropy density, respectively in the current configuration and are also functions of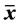 .
. 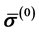 is the Cauchy stress tensor (in Eulerian description in contravariant basis). The superscript “0” is used to signify that it is rate of order zero and the lowercase parenthesis destinguish it from the second Piola-Kirchhoff stress tensor
is the Cauchy stress tensor (in Eulerian description in contravariant basis). The superscript “0” is used to signify that it is rate of order zero and the lowercase parenthesis destinguish it from the second Piola-Kirchhoff stress tensor 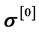 used in Lagrangian description. Dot on any quantity refers to the material derivative. As explained above undeformed and deformed configurations can be used in the derivatives as long as the final equations from the conservation and balance laws contain
used in Lagrangian description. Dot on any quantity refers to the material derivative. As explained above undeformed and deformed configurations can be used in the derivatives as long as the final equations from the conservation and balance laws contain 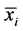 and t and do not have displacements and strains in them as these are not available for fluent continua. In the following a brief explanation of notations is necessary as some of the notations are new.
and t and do not have displacements and strains in them as these are not available for fluent continua. In the following a brief explanation of notations is necessary as some of the notations are new. 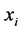 and
and 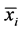 denote the position coordinates of a material point in the reference and current configurations, respectively, in a fixed frame (x-frame)
denote the position coordinates of a material point in the reference and current configurations, respectively, in a fixed frame (x-frame)
 (1)
(1)
or
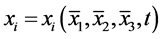 (2)
(2)
If 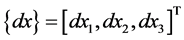 and
and 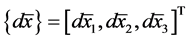 are the components of length
are the components of length  and
and  in the reference and current configurations, and if one neglects the infinitesimals of orders two and higher in both configurations, then one obtains
in the reference and current configurations, and if one neglects the infinitesimals of orders two and higher in both configurations, then one obtains


with

In Murnaghan’s notation

in which the columns of 











where

in which 

tensor, and 





The purpose of this paper is to present ordered rate constitutive theories for deviatoric Cauchy strain tensor, Cauchy moment tensor and heat vector for thermofluids without memory in which convected time derivatives of strain tensors up to order n are conjugate with the Cauchy stress tensor and the convected time derivatives of the symmetric part of the rotation gradient tensor up to orders 1n are conjugate with the Cauchy moment tensor.
2. Rotation Gradients, Their Convected Time Derivatives and Conservation and Balance Laws
In reference [1] [2] conservation and balance laws were derived for internal polar (non- classical) fluent continua. The derivations were presented using contravariant and covariant measures of stress, moment tensors as well as using Jaumann rates. Measures of stress, moment and strain tensors and their convected time derivatives in the respective bases can be considered. Following references [3] [4] for example






gradient tensor. Let 

(

the constitutive theories in contravariant basis, covariant basis and in Jaumann rates can be obtained. In addition to the convected derivatives of the strain tensors one must also consider convected derivatives of the rotation gradient tensor that are also basis dependent. In reference [3] the authors show that Cauchy moment tensor and symmetric part of the gradient of the rate of rotation tensor are conjugate. In reference [3] , the authors considered symmetric part of the gradients of rates of rotation obtained using skew symmetric part of the velocity gradient tensor. One notes that the Cauchy moment tensor is basis dependent: 
(


be the convected time derivatives of the rotation gradient tensors in contravariant basis, covariant basis, and Jaumann rates. With these convected time derivatives, the
conjugate pairs are (

(
laws as well as constitutive theories. Jacobian of deformation 


tors [4] . Thus, quantities derived using 
descriptions. Likewise 

of Jacobian of deformation. Rows of 



In finite deformation, a tetrahedron in the undeformed configuration with its orthogonal edges deforms into one in which the edges are non-orthogonal covariant base vectors and the vectors normal to the faces of the deformed tetrahedron are contravariant non-orthogonal base vectors that are reciprocal to the covariant base vectors. The covariant and contravariant bases are fundamental in the measures of finite deformation, rotations, etc. Consider deformed coordinates 


2.1. Covariant Basis: Internal Rotations, Rotation Matrix, Rotation Gradient Tensor and Their Convected Time Derivatives
(a) Internal rotations and rotation matrix
Consider decomposition of the Jacobian of deformation 



Let 
pressed as rotations about



in which

Alternatively one can also derive (15) as follows.




The sign differences between (15) and (18) are due to clockwise and counterclockwise internal rotations and will only affect sign of 











The stretch tensors 





1) 
2) 
3) Determination of 









4) It suffices to note that internal rotations at a material point present in 






5) The internal rotation angles 




(b) Internal rotation gradient tensor and its rates using
The covariant internal rotation tensor 

Let 

Alternatively (16) can be written as

and then

In (22) the internal rotations 





Then, one defines rotation gradient tensor 





One can also define the velocity gradients as

in which


Likewise if 




Remarks
1) Symmetric rotation gradient tensor in (26) is a covariant measure in Lagrangian description. It describes symmetric part of the gradients in x-frame of rotations about covariant axes expressed about the axes of the x-frame.
2) Since this measure is covariant rotation rate its work conjugate measure will be contravariant.
3) The covariant nature of this measure is intrinsic in its derivation due to


4) Convected time derivatives of 


(c) Second Piola-Kirchhoff covariant rotation gradient tensor
Consider isotropic, homogeneous, compressible matter. Let 











Thus, one obtains


using (36) and (37) in (34) one obtains

using (35) in (38)

hence, one obtains

and

Equations (40) and (41) are Lagrangian and Eulerian descriptions for second Piola- Kirchhoff covariant rotation gradient tensor. These are useful in deriving covariant convected time derivatives of the rotation gradient tensor

(d) Convected time derivatives of the covariant rotation gradient tensor: compressible matter
In this section derivation of convected time derivative of the covariant rotation gradient tensor 

One intentionally chooses Eulerian description for Cauchy and second Piola-Kir- chhoff tensor as this is what is needed in the case of mathematical model for fluent continua. Consider material derivative of

using


in (43), factoring and regrouping, one can write

If one defines


then one obtains the following from (46)





where

In general one can write the following recursive relations that can be used to obtain the convected time derivative of any desired order k of the covariant rotation gradient tensor 

For incompressible case 

2.2. Contravariant Basis: Internal Rotations, Rotation Matrix, Rotation Gradient Tensor and Their Convected Time Derivatives
(a) Internal rotations and rotation matrix
Following the derivations for covariant measures, one can derive the following if one considers Jacobian of deformation 





Let 




in which

Alternatively one can also derive (57) as follows.



The reason for the sign difference in (57) and (60) is exactly same as for covariant measures. One notes that decomposition (53) enables explicit description of stretches (elongation per unit length and change in angles between the pair of orthogonal material lines in the undeformed configuration) and rotation tensor contained in





The stretch tensors 





1) 
2) 
3) One notes that determination of 







4) It suffices to note that internal rotations at a material point present in 






5) The internal rotation angles 




(b) Internal rotation gradient tensor using
The contravariant internal rotation tensor 

Let 

Alternatively (62) can be written as

and then

In (64) the internal rotations 





Then the rotation gradient tensor 





Remarks
1) Symmetric rotation gradient tensor in (67) is a contravariant measure in Eulerian description. It describes symmetric part of the gradients of rotations about contravariant axes expressed about the axes of the x-frame.
2) Since this measure is contravariant its work conjugate moment measure is expected to be covariant (see derivation of first law of thermodynamics).
3) Contravariant nature of this measure is intrinsic in its derivation, hence can not be changed. However by replacing 

4) Convected time derivatives of 


(c) Second Piola-Kirchhoff contravariant rotation gradient tensor
Consider isotropic, homogeneous compressible matter. Consider oblique planes of the deformed and the undeformed tetrahedra with scalar areas 








Let the contravariant Cauchy rotation gradient tensor be 




Substituting (71) and (72) in (70)

using


Hence, one obtains

and

Also 


(d) Convected time derivatives of the contravariant rotation gradient tensor: compressible matter
Consider the material derivative of

using


and regrouping the terms one obtains

If one defines


then one can write

Here 

time derivative of the contravariant Cauchy rotation gradient tensor
material derivative of (84) and follows the same steps as in case of

where

In general one can write the following recursive relation that can be used to obtain the convected time derivative up to any desired order k of the tensor 

For incompressible case 

It is advantageous to introduce basis independent notations so that the derivations of conservation and balance laws could be carried out independent of the basis. These can then be made basis dependent by simply replacing the basis independent quantities. Similar to Cauchy stress tensor and Cauchy moment tensor, introduce 




2.3. Polar Decomposition of Velocity Gradient Tensor and Consideration of Local Rotation Rates
Polar decomposition of the velocity gradient tensor is helpful in decomposing deformation into stretch rate tensor and rotation rate tensor. Whether one uses left stretch rate tensor or right stretch rate tensor, the rotation rate tensor is unique. Thus, at each location with infinitesimal volume surrounding it, the velocity gradient tensor 















Let 



The columns of 




Then (89) holds, hence 


Thus, 


and following a similar procedure one can establish the following


in which 









where

Explicit forms of 














2.4. Conservation and Balance Laws
In reference [1] [2] conservation and balance laws were derived for internal polar fluent continua. These derivations were presented using




























At this stage the Cauchy stress tensor 






2.4.1. First Law of Thermodynamics: Energy Equation
The sum of work and heat added to a deforming volume of matter must result in the increase in energy of the system. Expressing this as a rate statement one can write [4] [9] [10] [11]







where 


placement, and 


tributes additional rate of work due to rates of rotation in (104). Expand each of the integrals in (102)-(104). Following reference [4] , it is straight forward to show that:



Using basis independent Cauchy stress tensor

Likewise using basis independent moment tensor (per unit area)

The first convected time derivative of the rotation gradient tensor,
that is conjugate to the Cauchy moment tensor 

Transferring all terms to left of equality and regrouping

Using (98) (balance of linear momenta) and (99) balance of angular momenta, (110) reduces to

Since 

Equation (113) is the final form of the energy equation in which 


In (114) the following decomposition of 

By appropriate choices of
2.4.2. Second Law of Thermodynamics: Entropy Inequality
If 








Using Cauchy’s postulate for 

Using (117) in (116)

One recalls that [4]

and

Substituting from (119) and (120) in (118) and transferring all terms to the left of inequality

Since volume 

Equation (122) is called the Clausius-Duhem inequality and is the most fundamental form resulting from the second law of thermodynamics. A different form of (122) can be derived if one assumes

where 



Substituting for 



From energy Equation (113) (after inserting 

Substituting from (126) into (125)

or

Let 

Hence

Substituting from (130) into (128)

or





The entropy inequality (132) in contravariant basis, covariant bases and in Jaumann rates can be obtained by replacing

3. Stress Decomposition and Balance Laws
It is instructive to decompose stress tensor 



where

Substituting these in the balance of linear momenta (98), balance of angular momenta (99), energy Equation (113), and entropy inequality (132) and noting that


as

one can write (137) as

Using (136)-(139) in (98), (99), (113), and (132) one can obtain




A simple calculation by expanding the terms shows that

By substituting (144) in (142) and (143) the energy equation and entropy inequality simplify.


Remarks
1) Equations (140), (141), (145), and (146) can also be expressed in contravariant basis, covariant basis and using Jaumann rates.
2) Equations (97), (140), (141), (145), and (146) constitute a complete mathematical model for internal polar fluent media in Eulerian description.
3) From (145) and (146) one can conclude that 









4) This mathematical model has closure once the constitutive theories for



4. Dependent Variables in the Constitutive Theories
The choice of dependent variables in the constitutive theories must be consistent with the axiom of casualty [4] [9] [10] . The self observable quantities and those that can be derived from them by simple differentiation and/or integration can not be considered as dependent variables in the constitutive theories. Thus velocities, temperatures, temperature gradients, etc. are ruled out as choices of dependent variables in the constitutive theories. From the entropy inequality one notes that 











Possible choices of argument tensors of dependent variables are considered, keeping in mind the principle of equipresence [4] [9] [10] , i.e. at the onset all dependent variables in the constitutive theories possibly must contain the same argument tensors. For compressible fluent media, density 














One notes that 






Similarly 






Secondly, since the arguments in (147) are basis dependent the heat vector is no longer



From the entropy inequality one notes that 
are conjugate pairs i.e. 

has no dependence on



5. Entropy Inequality and Constitutive Theories
Consider the entropy inequality (146) with the arguments of 


From the continuity Equation (97) (its alternate from in

Using (151) in (150)

One notes that

Using (153) in (152)

Substituting 

Regrouping terms in (155)

For (156) to hold for arbitrary but admissible








Equations (157)-(161) are fundamental relations from the entropy inequality
Remarks
1) Equation (157) implies that 

2) Equation (158) implies that 

3) Equation (159) implies that 

4) Based on (160), 



5) The last inequality is essential in the form it is stated. For example the following (or any other separation of terms)

are inappropriate due to the fact that these imply that 



In view of these remarks the arguments of the dependent variables in the constitutive
theories in (149) can be modified. One can use 


One notes that there are no mechanisms or conditions that permit eliminating 



5.1. Decomposition of Stress Tensor
In order to remedy the situation discussed in remark (5), one considers decomposition of symmetric Cauchy stress tensor into equilibrium Cauchy stress tensor 


in which one considers the following

That is 


vanishes when 


or

5.1.1. Constitutive Theory for Equilibrium Stress
Since 





in which



as a function of 




assumes the compressive pressure to be positive, then 


Inequality (170) is satisfied if

and

Inequalities (171) imply that the rate of work due to 




Constitutive theories for


5.1.2. Constitutive Theory for Equilibrium Stress
For incompressible matter density is constant, hence




The incompressibility condition must be enforced. Based on (174) one can add

to (167). 

Using 

In the case of incompressible internal polar thermofluids 






Inequality (179) will hold if

and

Conditions (180) and (181) are the same for the compressible case i.e. the rate of work due to 



Constitutive theories for


Remarks
1) Conditions resulting from the entropy inequality require decomposition of 


2) Use of stress decomposition (164) in the conditions resulting from the entropy inequality permits determination of the constitutive theory for equilibrium stress tensor for compressible as well as incompressible internal polar thermofluids in terms of thermodynamic pressure and mechanical pressure.
3) The inequalities (170) or (179) require the rate of work due to 



4) The inequality (172) or (181) can be used (shown later) to derive a simple constitutive theory for 

5) The equilibrium stress 


6) The rate constitutive theories for deviatoric Cauchy stress tensor, Cauchy moment tensor and heat vector are derived using theories of generators and invariants [4] [9] [12] - [27] .
5.2. Rate Constitutive Theories of up to Order n for Deviatoric Symmetric Cauchy Stress Tensor
Consider the following (from (173))

Let 







The coefficients 




To determine material coefficients from (186), one considers Taylor series expansion of each 




One notes that 
tions of






Collecting coefficients (quantities defined in


Using (189), one can write (188) as follows








5.3. Rate Constitutive Theories of up to Order n and 1n for Heat Vector
Consider (from (173))

Let 



Let 



The absence of unit vector in (192) is due to the fact that uniform temperature field does not contribute to












for 

Then, using (193) the resulting form of (192) can be written as









5.4. Constitutive Theory for Cauchy Moment Tensor
Consider the following (from (173))

Let 







The coefficients 



To determine the material coefficients from (197), one considers Taylor series expansion of each 





Then using (198) in (196) can be written as








5.5. Remarks
1) The constitutive theories for 



2) The configuration 


3) An important point to note is that the material coefficients in the final forms of the constitutive theories are defined in a known configuration
4) Using the derivations presented in Sections 5.2-5.4 rate constitutive theories of various orders in desired basis can be derived by choosing values of n and 1n, the orders of the rate theory. As the orders of the rate theory increase, the number of material constants increases significantly. Thus, the higher order rate theories necessitate elaborate experiments to calibrate them.
5) In the following rate theories of orders one (
5.6. Rate Constitutive Theories of Order One (

This is the simplest possible constitutive theory for 



In this case the combined generators of 



and the combined invariants of



Thus, one can write

Following the general derivations in Section 5.2 for N generators and M invariants, for this specific case one can write

The definitions of material coefficients 

remain the same as defined in (189). This constitutive theory requires 46 material coefficients, still too many to determine experimentally.
5.6.1. Simplified Rate Constitutive Theory of Order One (

Consider a constitutive theory in which 


In this case there are only two generators (


and the following constitutive theory (using (190) for 


This constitutive theory requires 14 material coefficients and contains up to fifth degree terms in the components of
5.6.2. Simplified Rate Constitutive Theory of Order One (


Begin with (204) and neglect those terms on the right side of (204) that are of degree higher than two in the components of

This constitutive theory requires 8 material coefficients.
If one further neglects the product terms in 

This constitutive theory requires only six material coefficients. The dependence of the material coefficients on the invariants in (209) can be modified based on the assumptions used here or can be maintained as originally defined in (189).
5.6.3. Simplified Rate Constitutive Theory of Order One (


If one neglects quadratic terms in 
for 


If one denotes 


Material coefficients 





5.7. Remarks on Constitutive Theories for
1) One notes that the arguments of 





2) Some specific remarks can be made for the simplified rate theory of order one given by (211). When one compares (211) with the similar theory for




Equation (211) implies that

Hence, one can write (211) as

That is, the linear constitutive theory of order one in (214) for deviatoric Cauchy stress tensor is basis independent.
3) Since the material coefficients 






5.8. Simplified Constitutive Theories for
The most general constitutive theory for Cauchy moment tensor 

5.8.1. Constitutive Theory for 

In this case

and 



The constitutive theory for 




The material coefficients in (218) are defined by (198).
5.8.2. Constitutive Theory for 


One begins with (218) and neglects those terms on the right side of (218) that are of degree higher than two in the components of

This constitutive theory requires eight material coefficients. If one further neglects the product terms in 

This constitutive theory requires only six material coefficients. The dependence of the material coefficients on the invariants in (220) can be modified based on the assumptions used here or can be maintained as originally defined in (198).
5.8.3. Constitutive Theory for 



If one denotes 


The material coefficients 







5.9. Remarks
In reference [3] instead of

gate of



be basis dependent i.e. it must be the convected time derivative of the rotation gradient tensor i.e. one must replace it with



where

Hence,

as

Thus

This is an approximation as 


Recall that

or

or

Likewise

or

or

Thus for small rates of rotation gradients one can write

Thus, (228) used in reference [3] is an approximation to the symmetric part of the convected time derivative of the rotation gradient tensor. Use of 

6. Summary and Conclusions
In this paper ordered rate constitutive theories of orders n and 1n are presented for internal polar non-classical, isotropic, homogeneous thermofluids in which the varying rates of rotations and conjugate moments in addition to usual thermofluid physics (classical) are considered in the derivations of the conservation and balance laws. The constitutive theories are presented in contravariant basis, covariant basis, and using Jaumann rates, but the derivation of the constitutive theories is carried out using basis independent stress tensor, heat vector, and moment tensor. By choosing these in the desired basis, basis dependent constitutive theories can be obtained. The theory of generators and invariants in conjunction with the conditions resulting from entropy inequality form the basis for the derivation of the constitutive theories.
The dependent variables in the constitutive theories are established by examining conservation and balance laws in conjunction with principle of casualty [4] [9] . By examining the conditions resulting from entropy inequality and after introducing stress decomposition one finally arrives at 

where 











as argument tensors of all dependent variables (based on principle of equipresence [4] [9] ) in the constitutive theories for thermofluids. Using the conjugate pairs in entropy inequality it is straightforward to eliminate 




and deviatoric tensors

thermodynamic pressure 


and
are established using theory of generators ad invariants. General constitutive theories of up to order n for








It is clearly shown in the paper that choice of 









The work presented in this paper removes the restriction of small rotation gradient rates due to use of 



Acknowledgments
The first and third authors are grateful for the support provided by their endowed professorships during the course of this research. The support and resources provided by the Computational Mechanics Laboratory (CML) of the Mechanical Engineering department of the University of Kansas is gratefully acknowledged. The financial support provided to the second author by the Department of Mechanical Engineering of the University of Kansas is greatly appreciated.
Cite this paper
Surana, K.S., Long, S.W. and Reddy, J.N. (2016) Rate Constitutive Theories of Orders n and 1n for Internal Polar Non-Classical Thermofluids without Memory. Applied Mathematics, 7, 2033- 2077. http://dx.doi.org/10.4236/am.2016.716165
References
- 1. Surana, K.S., Reddy, J.N. and Powell, M. (2015) A Polar Continuum Theory for Uent Continua. International Journal of Engineering Research and Industrial Applications, 8, 107-146.
- 2. Surana, K.S., Powell, M. and Reddy, J.N. (2015) A More Complete Thermodynamic Framework for Uent Continua. Journal of Thermal Engineering, 1, 1-16.
- 3. Surana, K.S., Powell, M. and Reddy, J.N. (2015) Ordered Rate Constitutive Theory for Internal Polar Thermouids. International J. of Math. Sci. & Engg. Appls., 9, 51-116.
- 4. Surana, K.S. (2015) Advanced Mechanics of Continua. CRC/Taylor & Francis Group, Boca Raton.
- 5. Steinmann, P. (1994) A Micropolar Theory of Finite Deformation and Finite Rotation Multiplicative Elastoplasticity. International Journal of Solids and Structures, 31, 1063-1084.
http://dx.doi.org/10.1016/0020-7683(94)90164-3 - 6. Srinivasa, A.R. and Reddy, J.N. (2013) A Model for a Constrained, Finitely Deforming, Elastic Solid with Rotation Gradient Dependent Strain Energy, and Its Specialization to von Kármán Plates and Beams. Journal of the Mechanics and Physics of Solids, 61, 873-885.
http://dx.doi.org/10.1016/j.jmps.2012.10.008 - 7. Segerstad, P.H., Toll, S. and Larsson, R. (2009) A Micropolar Theory for the Finite Elasticity of Open-Cell Cellular Solids. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Science, 465, 843-865.
- 8. Shield, R.T. (1973) The Rotation Associated with Large Strains. SIAM Journal on Applied Mathematics, 25, 483-491.
http://dx.doi.org/10.1137/0125048 - 9. Eringen, A.C. (1967) Mechanics of Continua. John Wiley and Sons, Hoboken.
- 10. Eringen, A.C. (1962) Nonlinear Theory of Continuous Media. McGraw-Hill, Boston.
- 11. Reddy, J.N. (2013) An Introduction to Continuum Mechanics. Cambridge University Press, Cambridge.
- 12. Smith, G.F. (1960) On the Minimality of Integrity Bases for Symmetric 3 × 3 Matrices. Archive for Rational Mechanics and Analysis, 5, 382-389.
http://dx.doi.org/10.1007/BF00252916 - 13. Smith, G.F. (1965) On Isotropic Integrity Bases. Archive for Rational Mechanics and Analysis, 18, 282-292.
http://dx.doi.org/10.1007/BF00251667 - 14. Smith, G.F. (1970) On a Fundamental Error in Two Papers of CC Wang on Representations for Isotropic Functions, Part I and II. Arch. Ratl. Mech. Anal, 36.
- 15. Smith, G.F. (1971) On Isotropic Functions of Symmetric Tensors, Skew-Symmetric Tensors and Vectors. International Journal of Engineering Science, 9, 899-916.
http://dx.doi.org/10.1016/0020-7225(71)90023-1 - 16. Spencer, A.J.M. (1961) The Invariants of Six Symmetric 3 × 3 Matrices. Archive for Rational Mechanics and Analysis, 7, 64-77.
http://dx.doi.org/10.1007/BF00250750 - 17. Spencer, A.J.M. (1965) Isotropic Integrity Bases for Vectors and Second-Order Tensors. Archive for Rational Mechanics and Analysis, 18, 51-82.
http://dx.doi.org/10.1007/BF00253982 - 18. Spencer, A.J.M. and Rivlin, R.S. (1958) Finite Integrity Bases for Five or Fewer Symmetric 3 × 3 Matrices. Archive for Rational Mechanics and Analysis, 2, 435-446.
http://dx.doi.org/10.1007/BF00277941 - 19. Spencer, A.J.M. and Rivlin, R.S. (1958) The Theory of Matrix Polynomials and Its Application to the Mechanics of Isotropic Continua. Archive for Rational Mechanics and Analysis, 2, 309-336.
http://dx.doi.org/10.1007/BF00277933 - 20. Spencer, A.J.M. and Rivlin, R.S. (1959) Further Results in the Theory of Matrix Polynomials. Archive for Rational Mechanics and Analysis, 4, 214-230.
http://dx.doi.org/10.1007/BF00281388 - 21. Spencer, A.J.M. and Rivlin, R.S. (1962) Isotropic Integrity Bases for Vectors and Second-Order Tensors. Archive for Rational Mechanics and Analysis, 9, 45-63.
http://dx.doi.org/10.1007/BF00253332 - 22. Wang, C.C. (1969) On Representations for Isotropic Functions. Archive for Rational Mechanics and Analysis, 33, 249-267.
http://dx.doi.org/10.1007/BF00281278 - 23. Wang, C.C. (1969) On Representations for Isotropic Functions. Archive for Rational Mechanics and Analysis, 33, 268-287.
http://dx.doi.org/10.1007/BF00281279 - 24. Wang, C.C. (1970) A New Representation Theorem for Isotropic Functions: An Answer to Professor GF Smith’s Criticism of My Papers on Representations for Isotropic Functions. Archive for Rational Mechanics and Analysis, 36, 166-197.
http://dx.doi.org/10.1007/BF00272241 - 25. Wang, C.C. (1970) A New Representation Theorem for Isotropic Functions: An Answer to Professor G. F. Smith’s Criticism of My Papers on Representations for Isotropic Functions. Archive for Rational Mechanics and Analysis, 36, 198-223.
http://dx.doi.org/10.1007/BF00272242 - 26. Wang, C.C. (1971) Corrigendum to My Recent Papers on Representations for Isotropic Functions. Archive for Rational Mechanics and Analysis, 43, 392-395.
http://dx.doi.org/10.1007/BF00252004 - 27. Pennisi, S. and Trovato, M. (1987) On the Irreducibility of Professor GF Smith’s Representations for Isotropic Functions. International Journal of Engineering Science, 25, 1059-1065.
http://dx.doi.org/10.1016/0020-7225(87)90097-8 - 28. White, F.M. (1991) Viscous Fluid Flow. McGraw-Hill, Inc., Boston.














