Applied Mathematics
Vol.07 No.17(2016), Article ID:72191,17 pages
10.4236/am.2016.717175
Analysis of SDEs Applied to SEIR Epidemic Models by Extended Kalman Filter Method
D. Ndanguza1, I. S. Mbalawata2, J. P. Nsabimana1
1Department of Mathematics, University of Rwanda, Kigali, Rwanda
2Department of Mathematics, University of Dar-es-Salaam, Dar-es-Salaam, Tanzania

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: April 14, 2016; Accepted: November 20, 2016; Published: November 23, 2016
ABSTRACT
A disease transmission model of SEIR type is discussed in a stochastic point of view. We start by formulating the SEIR epidemic model in form of a system of nonlinear differential equations and then change it to a system of nonlinear stochastic differential equations (SDEs). The numerical simulation of the resulting SDEs is done by Euler-Maruyama scheme and the parameters are estimated by adaptive Markov chain Monte Carlo and extended Kalman filter methods. The stochastic results are discussed and it is observed that with the SDE type of modeling, the parameters are also identifiable.
Keywords:
Epidemic Model, Estimation of Parameters, Extended Kalman Filter, Markov Chain Monte Carlo

1. Introduction
The mathematical modeling of different diseases continues to be an area of active research. The aim of epidemic modeling is to understand and, if possible, to control the spread of the disease. To do this, epidemic modeling tries to relate disease dynamics at the population level to basic properties of the host and pathogen populations and of the infection process. In order to model the progress of an epidemic in a large population, comprising many different individuals in various fields, the population diversity must be reduced to a few key characteristics which are relevant to the infection under consideration. For example, for most common childhood diseases that confer long-lasting immunity it makes sense to divide the population into those who are susceptible to the disease, those who are infected and those who have recovered and are immune (SIR epidemic model). These subdivisions of the population are called compartments. This idea has been extended to SEIR epidemic model where the population can be partitioned into four compartments: susceptible (S), latent or exposed (E), infectious (I), and recovered (R).
The mathematical modeling of SEIR diseases is largely done deterministically [1] [2] [3] [4] . For instance, dynamical biological processes are better modeled by means of systems of deterministic ordinary differential equations (ODE), partial differential equation (PDE), or delay differential equation (DDE) [5] . The ODEs explain how a system changes or evolves, when the change occurs and the effect of the starting point to the initial solution and so forth. However, such modeling does not take into consideration some of uncertainties. It is this reason that has forced us to model the SEIR with Ito stochastic differential equation. Our main concern is to incorporate uncertainties into a mathematical model which are modeled using probabilities.
The main advantage of deterministic modeling over stochastic modeling lay on the simplicity to analyze. Generally, the deterministic models are simple to analyze. However, stochastic models are to be used if their analysis is possible. As pointed out in [6] the stochastic modeling should be preferred over deterministic modeling because:
・ Most natural way of studying the spread of disease is stochastic because it defines the probability of transmission of disease between individuals. Stochastic modeling converges to deterministic modeling when the population size becomes large [7] .
・ Some phenomena are genuinely stochastic and do not satisfy the law of large number [8] .
・ The deterministic models are not the most relevant for modeling the start of an epidemic because the number of infectious individuals is small [5] .
・ Extinction of endemic diseases can only be analyzed by stochastic model because the extinction occurs when the epidemic process deviates from expected level [9] .
・ Estimation of parameters and states require the knowledge about uncertainty in estimates. Stochastic modeling enables estimation of parameters from disease outbreak data to be equipped with standard errors [10] .
・ Stochastic models are, in general, more realistic since the spread of diseases is stochastic in nature [11] .
One of the advantages, over some of the other stochastic formulations, of modeling using the SDEs is that the SDEs can be derived directly from the deterministic system of ordinary differential equations and have a relatively simple form [9] [12] [13] . However, sometimes the results from SDEs are similar to those corresponding to discrete and continuous-time Markov chain models [5] [8] .
As mentioned above, to use stochastic modeling we need to be able to analyze the phenomena stochastically, otherwise deterministic modeling should be used. In this paper, we model by Itȏ SDEs which are relatively simple and they can be easily derived directly from the deterministic system of ODEs [14] . In short, we convert the given deterministic model into SDE and then use the Bayesian sampling technique to analyze the resulting SDE. The conversion to SDEs for epidemic models has been discussed in [7] - [12] [14] .
In this paper, we provide a brief introduction to the Itô SDEs in Section 2 and the conversion of SEIR ODE to SDE is done in Section 3. In Section 4, the adaptive Markov chain Monte Carlo (MCMC) with the likelihood function computed by extended Kal- man filter is discussed. The numerical simulation and conclusion are found in Sections 5 and 6 respectively.
2. Itô Stochastic Differential Equation
The inclusion of random effects in differential equations can lead to either random differential equation whose solutions have differentiable sample paths or stochastic differential equations whose solutions have non-differentiable [5] . The stochastic differential equations (SDEs) are attracting much attention due to physical processes in real life systems experience random forcing and stochastic inputs that cannot be captured by ordinary differential equations. Therefore, our concern in this article is the SDEs which can be expressed in terms of It or Stratonovich SDE [5] [13] . The Ito SDE, where global Lipschitz and growth conditions are satisfied to ensure the existence and uniqueness of strong solutions, can be written as [5] [13] [15] .
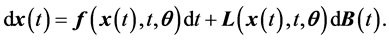 (1)
(1)
Here, is the set of SDE, is the drift vector function, 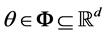 is the vector of parameters to be estimated,
is the vector of parameters to be estimated, 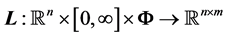 is a diffusion function, and is m-dimension Brownian motion with diffusion matrix
is a diffusion function, and is m-dimension Brownian motion with diffusion matrix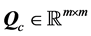 . If
. If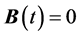 , the SDE becomes the normal ordinary differential equation.
, the SDE becomes the normal ordinary differential equation.
The analysis of stochastic differential equations including their numerical treatment is nowadays of crucial importance for applications in finance, modeling of particle systems for solving non-linear kinetic equations, epidemiology and other areas in applied mathematics. However due to non-differentiability character of realizations of the Brownian processes, it is difficult to simulate the SDEs. There exist numerical schemes for approximating the solution of SDE (1) [5] . In this paper, we use Euler-Maruyama scheme. The Euler-Maruyama discretization scheme is the simplest numerical scheme where the solution of the SDE (1) is approximated as [5] [16] [17]
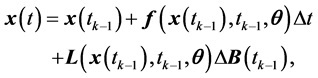 (2)
(2)
where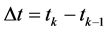 . For detail treatment of stochastic calculus and SDE theories a reader is referred to [5] [13] [18] .
. For detail treatment of stochastic calculus and SDE theories a reader is referred to [5] [13] [18] .
3. Model Framework
In this section, there is a description of a simple SEIR epidemic model for the transmission of infectious diseases where the population is assumed to be closed (the population does not contain the demographic changes) [4] . Hence, the assumption is that during the outbreak of the epidemic no births or natural deaths occur.
3.1. A SEIR Deterministic Model
Suppose the total effective population size N is divided in four compartments namely Susceptible individuals in class S, after being contacted with the virus enter the exposed class E at the per-capita rate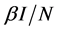 , where
, where 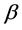 is the transmission rate per person per day,
is the transmission rate per person per day, 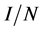 is the probability that a contact is made with an infectious individual. Exposed individuals undergo an average incubation period of
is the probability that a contact is made with an infectious individual. Exposed individuals undergo an average incubation period of 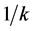 days before progressing to the infectious class I. Infectious individuals move to the R class (death or recovered) at the per-capita rate
days before progressing to the infectious class I. Infectious individuals move to the R class (death or recovered) at the per-capita rate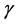 . This can be explained by the following transfer diagram in Figure 1.
. This can be explained by the following transfer diagram in Figure 1.
The transition process in modeled by the following system of nonlinear ordinary differential equations
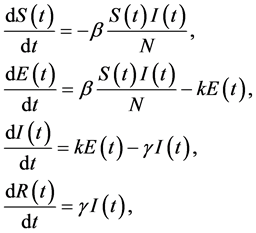 (3)
(3)
where 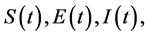 and
and 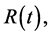 denote the number of susceptible, exposed, infected and removed at time t, respectively. It is seen that
denote the number of susceptible, exposed, infected and removed at time t, respectively. It is seen that 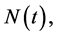 the population size
the population size
is constant because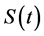 , and
, and 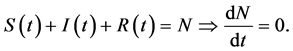 From (3) it is possible
From (3) it is possible
to express R in other variables 

Hence, (3) becomes
We solve the system (3), using Runge-Kutta numerical method and get the results represented by the two plots in Figure 2.
Since the population is closed, no recruitment to susceptible population but there is recruitment on other compartments. An individual reaching the compartment R will never come back to the system. According to the Figure 2, it is seen that the variable S is decreasing exponentially, whereas E and I are increasing and decreasing after a period of time. This is due to recruitment and migrations from those compartments. The compartment R is increasing exponentially because all individuals reaching this state are supposed to remain within it. The system of nonlinear ODE equations (4) will be used for all further studies and analysis. For numerical solutions of nonlinear ODEs see [19] for further information.
Figure 1. SEIR transfer diagram: recruitment and immigration among compartments.
Figure 2. SEIR epidemic model numerical simulation. The susceptible variable is decreasing since some of its candidates are immigrating to E. By this time, E and I are increasing and decrease after a given period. R is increasing exponentially. SEIR epidemic model numerical solutions are also fitted to simulated daily data. With these synthetic data we see that the model really fit them.
The deterministic dynamical processes in physics, engineering and epidemiology among other applications, changes in the system are studied over a small time interval and a differential equation is obtained as the time interval approaches zero. The dynamical system is carefully studied to determine all of the different independent random changes that occur in the system. Appropriate terms are determined for these changes in developing a discrete-time stochastic model which is then approximated by a system of stochastic differential equations [20] .
As it has been mentioned above, noises have crucial effects in epidemic models which motivates researchers to change the system of SEIR ODEs into a system of SEIR SDEs.
3.2. Equivalent SEIR Stochastic Model
SDEs of the Ito type are derived from a system of ordinary differential Equation (3). This will be done using method found in [9] [10] [11] . Let 


The transition probabilities are represented by the following equation:
Note that i, j, l and m are integers defined in [1] [2] [4] . To form the SDE model (5) using the procedure developed by [9] , 

The ODE system (4) will be converted into the SDE in the form [11]

where 


Let u compute the covariance matrix as follows
Table 1. Compartment changes in a small time period
It follows that the SDE model for this problem has the form:

4. Parameters Estimation of Stochastic Differential Equation
It is easy to form the stochastic differential equation (SDE), however, in practice the parameters of the resulting SDE model remain uncertain or completely unknown. There are many methods for estimating such parameters; generalized moment methods, the efficient moment methods, exact likelihood inference methods, pseudo likelihood methods, simulated likelihood methods indirect inference methods, filtering based methods, least square methods sequential Monte Carlo, maximum likelihood, quasi maximum likelihood, kernel density method, local linearization, least squares, gene- ralized method of moments, minimum 
Recently [26] developed a new method of estimating parameters of SDEs using non- linear Kalman filter and Markov chain Monte Carlo (MCMC). In their method, [26] compute the energy and energy derivative functions using linear Kalman filter and extended Kalman filter for linear and nonlinear SDEs respectively. Having energy function and its derivative, once can estimate SDE parameters using gradient free and gradient based methods. For our case, we use the filtering method developed in [26] to estimate the unknown parameters


4.1. Continuous-Discrete Extended Kalman Filter
In filtering based approximation methods, the idea is to use measurement model (8) in a recursive way to estimate the states and compute sufficient statistics of the dynamic model (7). For linear SDE, one can use Kalman filter [27] to compute the posterior distribution of states, where the predictive differential equations are analytically solved by matrix fraction decomposition [26] . This idea of computing sufficient statistics using Kalman filter cannot be used in our nonlinear SDE (6) because Kalman filter is only for linear dynamic model [28] [29] .
For the case of nonlinear SDE, [26] uses extended Kalman filter (EKF) to compute the (unnormalized) negative logarithm-posterior function and it’s derivative used in MCMC samplers. The continuous-discrete EKF is a Taylor series expansion based approximation of the general Bayesian continuous-discrete filter [28] . In our resulting SDE (6) numerical simulations, we choose measurement noises which are additive hence the non-linear continuous discrete filtering problem can be stated as


where 
















In continuous-discrete EKF approach there are two steps; prediction and update steps [26] :
1. Prediction step:


where 






2. Update step:





where 

Using the Gaussian approximation of the posterior distribution computed from the continuous-discrete EKF, the negative logarithm posterior function can be approximated as follows [26] :

4.2. Markov Chain Monte Carlo
Markov chain Monte Carlo (CMC) methods (see, e.g., [30] ) are numerical methods for computing multidimensional integrals of the above form by using Monte Carlo. The idea is to draw samples 


One difficult in drawing samples from the posterior distribution is that even for the evaluation of the posterior probability density; we would need to be able to evaluate the normalization constant integral. MCMC methods are a class of Monte Carlo methods, which can draw the samples without the knowledge of the normalization constant. These methods are based on simulating a multidimensional Markov chain, which has been constructed such that it has the posterior distribution as its stationary distribution. In the simulation of the Markov chain we only need to evaluate the ratios posterior probability densities and thus the evaluation of the normalization constant is not required.
The most well-known MCMC methods are the Metropolis, Metropolis-Hastings and Gibbs sampler algorithms [30] . The Metropolis-Hastings MH algorithm works by sampling a candidate point 

1. Draw a candidate point, 

2. For
・ Sample a candidate point 

・ Accept the candidate point and set 

・ Generate 
・ Accept 

If the proposal distribution is symmetric we have Metropolis algorithm whose acceptance probability (18) reduces to

In general, the proposal distribution used in MCMC algorithm should result in well mixing of chains and in a suitable acceptance rate. Determining which proposal distribution is the best one for a particular target distribution is a very important, but also a difficult task, because it involves much trial-and-error. The most used proposal distribution is the Gaussian distribution; however, we do not know how to obtain a suitable covariance matrix. One way to overcome this problem is to use adaptive MCMC where the proposal distribution is automatically adapted during the MCMC run [31] [32] [33] [34] . We present below the adaptive MCMC developed by [13] .
i. Initialization: start with the initial values 





ii. At each step, propose a new 

iii. Accept/reject 
iv. For 

where 




iv. Iterate from ii. Above until you get enough samples.
5. Numerical Simulations
In this section, we employ the continuous-discrete extended Kalman filter to estimate the parameters of our resulting SDE (6). For the case of measurement model, the measurement function is assumed to be linear with measurement covariance 


Running EKF result into state estimate and other sufficient statistics. Figure 3 shows the EKF estimates of the compartments with their corresponding true states. The Susceptible population is decreasing while the Exposed and Infected ones are increasing from the beginning till a certain time t where it starts decreasing to be zero. This means that the disease is controlled and is being eradicated to die out from the population. This numerical solution is in agreement with deterministic SEIR ODE equations.
Figure 3. Simulated compartments and EKF estimates: from the figure Sx, and Ix represent simulated data for susceptible, exposure and infected while Sekf, and Iekf represent estimated compartments data for susceptible, exposure and infected.
To test if the extended Kalman filter likelihood based computation works, we use a grid based method where each parameter is estimated separately. For instance, if we want to identify 






The trend of generated samples can be studied using the trace plots Figure 5. It is seen that the contact rate 

The basic reproduction number

mission intensity and establishes threshold criteria [35] . It is known that if the basic reproduction number 


The autocorrelation functions measure how well the MCMC sampler is performing by measuring the autocorrelation between 

Figure 4. Grid based estimation methods: The y axis shows the log-posterior values while the x axis shows the range of corresponding parameter values. The first plot shows the log-posterior distribution for β, keeping other parameters fixed. The same explanation applied to the second and third plots but this time for k and γ respectively. Generally, the method shows that the parameters of SEIR can be identifiable using any likelihood based methods.
Figure 5. Trace plots.
from Figure 7 are decreasing and stabilizing around zero, this indicates that the parameters are identifiable.
The marginal distributions of parameters for HMC and MH samples, together with mean, median and MAP estimate, are shown in Figure 8. The distributions are not
Figure 6. The histogram and probability density function of the basic reproductive number.
Figure 7. Autocorrelation functions.
symmetric distributed as the right tails elongate more than left tails, though the mean, median and MAP estimates are around the center of the distribution. For all samples, the coefficient of skewness is greater than 0, hence the marginal distributions are skewed to the right. For the case of kurtosis coefficients values, the values are greater than 3 for 

Figure 8. Marginal distribution of samples.
the normal distribution. The kurtosis value for k samples was found to be less than 3, which indicates that the marginal distribution is not more peaked than normal distribution.
6. Conclusions
SEIR epidemic model has been studied by many scholars but in different approaches where all are almost focusing to the same results. The S-E-I-R model discussed in this paper assumes a closed community. In other words, all the n individuals in the community do not leave the system, and eventually all will be infected if no means of stopping such outbreak are set out. Even in more sophisticated models, such an assumption is sometimes necessary in order to reach a solution. The question is not how many susceptible individuals will become infectious (since, according to the model, all will be infected), but perhaps how quickly the epidemic is spreading and when the spread will slow down. Many methods of the parameter estimation of systems of ODE models have been developed and are now being applied in different areas of research. Although these are useful instruments, they are essentially deterministic in nature, and are not capable of capturing uncertainties or noise into the model. Stochastic models are to be preferred when their analysis is possible; otherwise deterministic models should be used. Deterministic models can also serve as introductory models when studying new phenomena. We see that there is no conflict between the two approaches and believe that both types of models play an important role in better understanding the mechanisms of disease spread.
On the side of SDEs epidemic models few approaches of estimating parameters have been developed. In this paper, we have used the adaptive Markov chain Monte Carlo with extended Kalman filter to estimate the parameters of nonlinear SDE. One can use other nonlinear filtering methods like Gaussian filter, or particle filters. The motivation of this research was to investigate if model parameters are also affected by random fluctuations after changing the deterministic ODEs to stochastic differential equations. The numerical simulations of epidemic SDEs are in agreement with deterministic SEIR epidemic model. It is not the intention of this paper to construct an accurate stochastic model for any disease outbreak but instead, through simulation runs of the MATLAB software programs, it serves to provide a way for readers to experiment with SDEs using a simple case of a disease outbreak.
Last but not least, it will be unfair to not mention that there is a wide range of models, both stochastic and deterministic, for the spread of an epidemic. Usually, when the population is constituted of a large number of individuals, a deterministic model is useful as a first approximation, and random variations can be neglected. As an alternative, a stochastic model could be more appropriate for describing the epidemic, but it is less tractable and its mathematical analysis is usually possible only when the population size is very small.
Acknowledgements
The authors acknowledge the contributions of many people to this work, in particular, Prof. Heikki Haario, for his encouragements and reviewers for their valuable comments. We also acknowledge the funding support provided by Eastern Africa Universities Mathematics Programme (EAUMP)-University of Rwanda node.
Cite this paper
Ndanguza, D., Mbalawata, I.S. and Nsabimana, J.P. (2016) Analysis of SDEs Applied to SEIR Epidemic Models by Extended Kalman Filter Method. Applied Mathematics, 7, 2195-2211. http://dx.doi.org/10.4236/am.2016.717175
References
- 1. Hethcote, H.W. (1989) Three Basic Epidemiological Models. In: Applied Mathematical Ecology, Springer, Berlin, 119-144.
https:/doi.org/10.1007/978-3-642-61317-3_5 - 2. Hethcote, H.W. and Levin, S.A. (1989) Periodicity in Epidemiological Models. In: Applied Mathematical Ecology, Springer, Berlin, 193-211.
https:/doi.org/10.1007/978-3-642-61317-3_8 - 3. Li, G. and Jin, Z. (2005) Global Stability of a Seir Epidemic Model with Infectious Force Inlatent, Infected and Immune Period. Chaos, Solitons & Fractals, 25, 1177-1184.
https:/doi.org/10.1016/j.chaos.2004.11.062 - 4. Ndanguza, D., Tchuenche, J.M. and Haario, H. (2013) Statistical Data Analysis of the 1995 Ebola Outbreak in the Democratic Republic of Congo. Afrika Matematika, 24, 55-68.
https:/doi.org/10.1007/s13370-011-0039-5 - 5. Kloeden, P.E. and Platen, E. (1999) Numerical Solution to Stochastic Differential Equations. Springer, Berlin.
- 6. Andersson, H. and Britton, T. (2000) Stochastic Epidemic Models and Their Statistical Analysis. Volume 151. Springer, New York.
https:/doi.org/10.1007/978-1-4612-1158-7 - 7. Allen, L.J.S. and Driessche, P.V. (2006) Stochastic Epidemic Models with a Backward Bifurcation. Mathematical Biosciences and Engineering: MBE, 3, 445-458.
https:/doi.org/10.3934/mbe.2006.3.445 - 8. Allen, E.J. and Victory, H.D. (2003) Modelling and Simulation of a Schistosomiasis Infection with Biological Control. Acta Tropica, 87, 251-267.
https:/doi.org/10.1016/S0001-706X(03)00065-2 - 9. Allen, E.J. (2007) Modeling with It? Stochastic Differential Equations. Springer, Dordrecht, The Netherlands.
- 10. Allen, L.J.S. and Allen, E.J. (2003) A Comparison of Three Different Stochastic Population Models with Regard to Persistence Time. Theoretical Population Biology, 64, 439-449.
https:/doi.org/10.1016/S0040-5809(03)00104-7 - 11. Allen, E.J., Allen, L.J.S., Arciniega, A. and Greenwood, P.E. (2008) Construction of Equivalent Stochastic Differential Equation Models. Stochastic Analysis and Applications, 26, 274-297.
https:/doi.org/10.1080/07362990701857129 - 12. McCormack, R.K. and Allen, L.J.S. (2004) Stochastic Sis and Sir Multihost Epidemicmodels. Conference on Differential Equations and Applications, 32, 775-785.
- 13. Øksendal, B. (2003) Stochastic Differential Equations: An Introduction with Applications. 6th Edition, Springer, Berlin.
https:/doi.org/10.1007/978-3-642-14394-6 - 14. Kirupaharan, N. and Allen, L.J.S. (2004) Coexistence of Multiple Pathogen Strains Instochastic Epidemic Models with Density-Dependent Mortality. Bulletin of Mathematical Biology, 66, 841-864.
https:/doi.org/10.1016/j.bulm.2003.11.007 - 15. Evans, L.C. (2012) An Introduction to Stochastic Differential Equations, Volume 82. American Mathematical Society, Providence, RI.
- 16. Burrage, K., Burrage, P. and Mitsui, T. (2000) Numerical Solutions of Stochastic Differential Equations-Implementation and Stability Issues. Journal of Computational and Applied Mathematics, 125, 171-182.
https:/doi.org/10.1016/S0377-0427(00)00467-2 - 17. Fard, O. (2007) A Numerical Scheme to Solve Nonlinear Stochastic Differential Equation. International Journal of Computational & Applied Mathematics, 2, 101-113.
- 18. Karatzas, I. (1991) Brownian Motion and Stochastic Calculus. Volume 113. Springer, Berlin.
- 19. Butcher, J.C. (2003) Numerical Methods for Ordinary Differential Equations. John Wiley & Sons, Hoboken.
https:/doi.org/10.1002/0470868279 - 20. Malyutin, V. (2005) Approximation to the Solution of the System of Nonlinear Stochastic Differential Equations. Computational Methods in Applied Mathematics, 5, 410-421.
- 21. Nielsen, J.N., Madsen, H. and Young, P.C. (2000) Parameter Estimation in Stochastic Differential Equations: An Overview. SIAM Journal on Numerical Analysis, 24, 83-94.
- 22. Shoji, I. and Ozaki, T. (1998) Estimation for Nonlinear Stochastic Differential Equations by a Local Linearization Method. Stochastic Analysis and Applications, 16, 733-752.
https:/doi.org/10.1080/07362999808809559 - 23. Singer, H. (2004) A Survey of Estimation Methods for Stochastic Differential Equations. Proceedings of 6th International Conference on Social Science Methodology, Amsterdam, 1-12.
- 24. Sørensen, H. (2004) Parametric Inference for Diffusion Processes Observed at Discrete Points in Time: A Survey. International Statistical Review, 72, 337-354.
https:/doi.org/10.1111/j.1751-5823.2004.tb00241.x - 25. Young, P. (1980) Parameter Estimation for Continuous-Time Models: A Survey. Automatica, 17, 23-39.
https:/doi.org/10.1016/0005-1098(81)90082-0 - 26. Mbalawata, I.S., Särkkä, S. and Haario, H. (2013) Parameter Estimation in Stochastic Differential Equations with Markov Chain Montecarlo and Non-Linear Kalman Filtering. Computational Statistics, 28, 1195-1223.
https:/doi.org/10.1007/s00180-012-0352-y - 27. Kalman, R.E. (1960) A New Approach to Linear Filtering and Prediction Problems. Transactions of the ASME, 82, 35-45.
https:/doi.org/10.1115/1.3662552 - 28. Jazwinski, A.H. (1970) Stochastic Processes and Filtering Theory. Academic Press, Pittsburgh.
- 29. Särkkä, S. (2013) Bayesian Filtering and Smoothing. Cambridge University Press, Cambridge.
https:/doi.org/10.1017/CBO9781139344203 - 30. Gilks, W.R., Richardson, S. and Spiegelhalter, D.J. (1996) Markov Chain Monte Carloin Practice. Chapman and Hall/CRC, Boca Raton.
- 31. Andrieu, C. and Thoms, J. (2008) A Tutorial on Adaptive MCMC. Statistics and Computing, 18, 343-373.
https:/doi.org/10.1007/s11222-008-9110-y - 32. Haario, H., Laine, M., Mira, A. and Saksman, E. (2006) DRAM: Efficient Adaptive MCMC. Statistics and Computing, 16, 339-354.
https:/doi.org/10.1007/s11222-006-9438-0 - 33. Haario, H., Saksman, E. and Tamminen, J. (2001) An Adaptive Metropolis Algorithm. Bernoulli, 7, 223-242.
https:/doi.org/10.2307/3318737 - 34. Liang, F., Liu, C. and Carroll, R.J. (2010) Advanced Markov Chain Monte Carlo Methods: Learning from Past Samples. John Wiley & Sons Ltd., Chichester.
https:/doi.org/10.1002/9780470669723 - 35. Diekmann, O., Heesterbeek, J.A.P. and Metz, J.A.J. (1990) On the Definition and the Computation of the Basic Reproduction Ratio R0 in Models for Infectious Diseases in Heterogeneous Populations. Journal of Mathematical Biology, 28, 365-382.
https:/doi.org/10.1007/BF00178324





















