Received 7 March 2016; accepted 25 April 2016; published 28 April 2016

ABSTRACT

In a polluted environment, considering the biological population infected with a kind of disease and hunted by human beings, we formulate a nonautonomous SIR population-epidemic model with time-varying impulsive release and general nonlinear incidence rate and investigate dynamical behaviors of the model. Under the reasonable assumptions, the sufficient conditions which guarantee the globally attractive of the disease-free periodic solution and the permanence of the infected fish are established, that is, the infected fish dies out if, whereas the disease persists if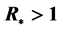. To substantiate our theoretical results, extensive numerical simulations are performed for a hypothetical set of parameter values.

Keywords:

Nonautonomous SIR Model, Varying Pulses, General Nonlinear Incidence Rate, Global Attractivity

1. Introduction

It is well known that Poyang Lake located in the middle and lower reaches of the Yangtze River is the current largest freshwater lake in China. Its wetland ecosystem has a significant impact on the change of China’s environment. The sufficient water resource and the superior natural environment nurture the abundant aquatic living resources of Poyang Lake. There are 136 kinds of fishes, 87 kinds of shells, 102 kinds of aquatic vascular plants and 266 kinds of identified plankton in Poyang Lake. The fishes in Poyang Lake take up 16.39% of the fresh water fish varieties in China, and 36.76% of the fish varieties of Yangtze River system. There are also first-level and second-level national protected precious rare aquatic animals such as white-flag dolphin, cowfish, chinese sturgeon, hilsa herring and so on in Poyang Lake, making it known as the treasury of fishery resources and the fish species genetic base with a significant position in the ecology system of the fish industry of Yangtze River reaches [1] .

At present, the grand development of Poyang Lake ecological economy is under way in a large scale in province, which promotes the establishment of the ecological economy zone [2] . However, the rapid economic development of Poyang Lake will have a negative influence on the living circumstances of fishes in the area. For the past few years, with the rapid development of modern industry and agriculture, a great quantity of toxicant and contaminants enter into Poyang Lake wetland ecosystem one after another. In order to use and regulate toxic substances wisely, we must assess the risk of the populations exposed to toxicant. Therefore, it is very important to investigate the effects of toxicants on populations and to find a theoretical threshold value, which determines permanence or extinction of fish population or community.

In recent years, many scholars have been conducted to investigate the effect of toxicant emitted into the environment from industrial, agricultural and household sources on biological species [3] - [19] by using mathe- matical models. For instance, Wang and Ma [18] investigated a nonautonomous SIS epidemic model with toxicant influence. They showed the existence and global attractiveness of periodic solutions and obtained the threshold between extinction and weak persistence of the infected class. Liu and Duan [19] considering the biological population infected with some kinds of diseases and hunted by human beings, and they formulate two SI pollution-epidemic models with continuous and impulsive external effects, respectively, and investigate the dynamics of such systems. But these previous models have invariably assumed that the exogenous input of toxicant is continuous or emitted in regular pulses. However, in the real life, it is often the case that toxicant is emitted in irregular pulses. In this paper, according to the above biological background, we investigate a nonautonomous SIR population-epidemic model with time-varying impulsive release and general nonlinear incidence rate and study dynamical behaviors of the model.

The organization of this paper is as follows. In the next section, we give some useful notations, definitions and preliminary lemmas which will be used to proof our main results. In Section 3, we mainly investigate a nonautonomous mathematical model with general nonlinear incidence rate and time-varying impulsive release, under some assumptions and the biological interpretation. In Section 4, we show that global attractivity of the disease-free periodic solution is determined by the threshold parameter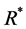. In Section 5, we give another expression of threshold parameter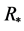, and show that if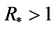, the disease is permanent. In the last section, we give a brief discussion and some numerical simulation results which conform the theoretical conclusions.

2. Notations, Definitions and Preliminary Lemmas

In this section, we introduce some notations, definitions and state some lemmas which will be useful in the subsequent sections. Let C denote the space of all bounded continuous functions. Given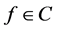, we let

If f is w-periodic, then the average value of f on a time interval 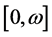can be defined as

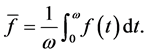
Before demonstrating the global attractivity of disease-free periodic solution of system (7), we need to intro- duce an important lemma.

Lemma 1. (see [20] ) Consider the following nonautonomous linear differential equation:

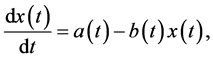
where 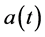and 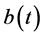are continuous and positive w-periodic functions. Then the system has a unique posi- tive w-periodic solution which is globally asymptotically stable.

3. Model Formulation and Preliminary

First of all, the total freshwater fish is divided into three groups: Susceptible fish (S), Infected fish (I) and Re- moved fish (R). Motivated by the above works and these literatures [21] - [29] , now we investigate the properties of fish’s dynamical behaviour of the model and human intervention in the polluted environment. The system is modeled by the following equations:

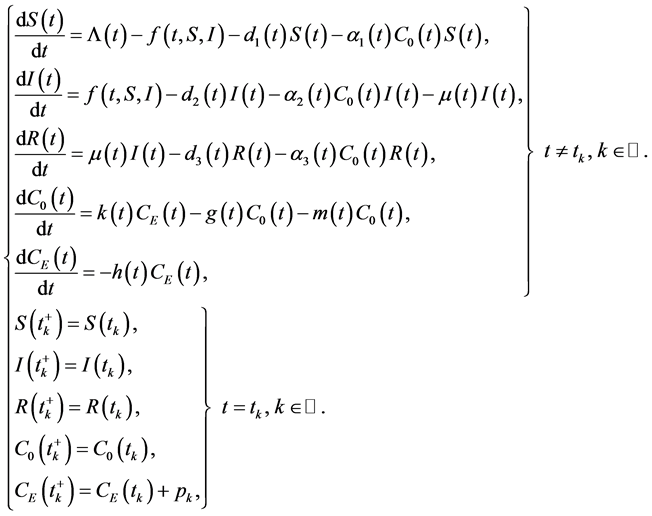(1)

The model is derived with the following assumptions.

・ , and represent the density of susceptible fish, infected fish and removed fish at time, respectively. The initial conditions are, and.

・ , and are left continuous for, that is, , and.

・ , are the instantaneous recruitment rate, death rate at time t, respectively. is the dose response parameter of the susceptible, infected and removed populations.

・ and represent the concentration of population in the organism and in the environment at time t, respectively. represents the organisms net uptake of population from the environment. and represent the egestion and depuration rates of population int the organism, respectively. represents the loss of population in the environment due to natural degradation.

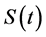・ The coefficients, , , , , , and are assumed

to be nonnegative, continuous and bounded w-periodic functions in the interval.

・ There exists a positive integer q such that for all. The exogenous quantity of impul- sive input of toxin into the environment is represented by at each fix time, and for

・ The general nonlinear incidence rate is a piecewise continuous, nonnegative, periodic function with period. The form of is as follows:

for all integer, and, for.

In the following, we give some basic properties of the following subsystem of model (1), which are very im- portant for deriving our main results.

(2)

where,.

Lemma 2. System (2) has a unique positive w-periodic solution which is globally asymptotically stable, where

(3)

(4)

for, ,

Proof. Integrating and solving the first equation of system (2) between pulses for, , ,

where

and be the initial value at time.

It follows from above equation and using the third equation of system (2), we get

and

Obviously, , using the inductive method, we have

(5)

Set. From (5) and, we have

(6)

f is the stroboscopic map. It is easy to see that system (6) has a unique positive equilibrium:

Since is a straight line with slope less than 1, we obtain that is globally asymptotically stable. It implies that the corresponding periodic solution of system (2) is globally asymptotically stable. Furthermore, according to Lemma 1, we can obtain that the system (2) has a unique positive -periodic solu- tion which is globally asymptotically stable. Therefore, the limit system of (1) is as follows:

(7)

By Lemma 1, it is easy to see that system (7) has a unique disease-free periodic solution

4. Global Attractivity of the Disease-Free Periodic Solution

To discuss the attractivity of the disease-free periodic solution of system (7), we firstly give the following hypothesis:

(A) There exist positive, continuous, periodic functions with period, such that , for all, and.

Theorem 1. If and system (7) satisfies the Hypothesis (A), then the disease-free solution is globally attractive, where

(8)

Proof. Let be any solution of system (7). Since, we can choose a sufficiently small number such that

From the second equation of system (7), we obtain that

By the comparison theorem, we can get that there exists a constant such that

(9)

for all.

It follows from (9) and the second equation of system (7) that, for

,

Then, we obtain that

(10)

By using the similar method, we can infer that for

Especially, when, we have

Therefore, we have for any positive integer. It follows from (9) that

(11)

From the (10) and (11), we get

(12)

Therefore, for above mentioned, there exist, we have

(13)

for all. From the first and third equation of system (6) and (12), we have for,

and

where is a sufficiently small number. Thus, we get

(14)

By using the similar method, we can see that

and

where is an arbitrary small. Therefore, we also obtain that

(15)

From (14) and (15), we can see that the disease-free periodic solution is global attractive.

5. Permanence of the Disease

In this section, we mainly obtain the sufficient conditions for the permanence of system (7). Therefore, we give the following hypotheses at first.

(B) There exist positive, continuous, periodic functions with the periodic, such that , for and. Denote be the solution of the following system:

According to Lemma 1, we can obtain that the system has a unique positive w-periodic solution which is globally asymptotically stable.

Theorem 2. If and system (7) satisfies the Hypotheses (A) and (B), then system (7) is permanent, where

(16)

Proof. Since, we can easily see that there exists a sufficiently small such that

In order to illustrate the conclusion, we firstly obtain the disease is uniformly weakly persistent, that is, there

exists a positive constant, such that. By contradiction, we have that, for all given

, there exists a such that for all.

In view of the Hypothesis (A) and the first equation of system (7), we get

By comparison theorem, we have and as, where is the solu- tion of the following comparison system:

Therefore, for above mentioned, there exists a, such that

(17)

for all.

For above mentioned, we have know that there exists a positive integer n₁ such that. Then for all , by (17) and the second equation of system (6), we have

Then we obtain that

By using the similar method, we can get that for

Furthermore, when, we have

(18)

Therefore, for any positive integer, we have. It follows from (18) that

From above, we obtain that, which is a contradiction to. Thus the claim is proved, that is, there exists a such that.

Therefore, the claim is proved.

By the claim, we are left to consider the following two possibilities:

Case 1. for t large enough;

Case 2. oscillates about for t large enough.

Define and. We hope to show that for t

large enough. The conclusion is evident in the first case. For the second case, let and satisfy

and for, where is large enough, such that

for. is uniformly continuous. Hence, there is a (, and is independent of

the choice of) such that for. If, there is nothing to prove. Let us consider

the case, there are two possible cases for.

(1) If, then from system (7), we have

(19)

It follows from (19) and, we get

Let, then for all.

(2) If, then from the discussion in subcase (1), we have for all. Next, we show that for all. Otherwise, there exists a constant such that

On the other hand, similar to discussion in subcase (1), it is easy to know that we can choose a proper, such that

Since is a continuous function, that is

for hold. Then for, we have

Then, , for, which is a contraction. Therefore, for

.

Since this kind of interval is chosen in an arbitrary way (we only need to be large enough).

Thus, we see that for any. We conclude that for t large enough.

According to our above discussion, the choice of is independent of the positive solution of system (7), and we have proved that any solution of system (7) satisfies for sufficiently large t, that is,

. It is easy to obtain that, there exist positive constants such that. There-

fore, system (7) is permanent.

6. Numerical Simulation and Conclusion

In this paper, we have constructed an impulsive equation to model the process of periodic release of toxicant at time-varying and studied the effect of toxicant on the fish population. From a biological point of view, the most interesting results are the following. On the basis of Theorems 1 and 2, we can see that and are the threshold condition under the species and become permanent or not. Under the reasonable assumptions, we have showed that if, the infected fish population dies out, and the disease-free periodic solution is globally asymptotically attractive. That is, if and the Hypotheses (A) and (B) hold, the infected fish population persists.

In the following, we will give some numerical simulations to illustrate the usefulness of the results and study the impact of impulsive release strength on the basic reproductive number. Numerical values of parameters of system (1) are given in Table 1. For the simulations that follows, we apply this set of parameters unless other- wise stated.

We let, , , , , , and (see Table 1), then. According to Theorem 1, we know that the disease will disappear. From Figure 1, we can also observe the disease will die out. If we choose q = 4, , , , , , and (see Table 1), then. According to Theorem 2, we get that the disease will be permanent (see Figure 2). Our results cannot solve the basic reproduction number of system (8). This, of course, shows that our results have a lot of room to improve.

Acknowledgements

The research has been supported by the Natural Science Foundation of China (11261004, 11561004), the Natural Science Foundation of Jiangxi Province (20151BAB201016), and the Science and Technology Plan Pro- jects of Jiangxi Provincial Education Department (GJJ14673, GJJ150984, GJJ150995). The Supporting the Development for Local Colleges and Universities Foundation of China-Applied Mathematics Innovative Team Building.

Cite this paper

Fumin Zhang,Shujing Gao,Yujiang Liu,Yan Zhang, (2016) Dynamics of a Nonautonomous SIR Model with Time-Varying Impulsive Release and General Nonlinear Incidence Rate in a Polluted Environment. Applied Mathematics,07,681-693. doi: 10.4236/am.2016.77062

References