Received 28 September 2015; accepted 22 November 2015; published 25 November 2015

ABSTRACT

In the Inverse Set relative to a Semivalue, we are looking for a new game for which the Semivalue of the original game is coalitional rational. The problem is solved by means of the Power Game of the given game. The procedures of building the new game, as well as the case of the Banzhaf Value are illustrated by means of some examples.

Keywords:

Semivalues, Power Game, Power Core, Coalitional Rationality

1. Introduction

In an earlier work of the author [1] , the Inverse Problem for the Shapley Value has been introduced and solved: for whatever n-vector, find out the set of all TU games for which the Shapley Value equals that a priori given vector. In a more recent work [2] , the Inverse Problem was solved for Semivalues, including the Banzhaf Value. Like in the first case, the solution was called the Inverse Set, relative to the Semivalue, and was given by an explicit formula expressing all games associated with that Semivalue, defined by a fixed weight vector. In a recent work [3] , it was also reminded that the Shapley Value, may not be coalitional rational, that is, in general, it does not belong to the Core of the game. In [3] , another problem was introduced and solved: given a TU game, for which we know the Shapley Value, or some other efficient value, find out a game with the same Shapley Value, or the alternative efficient value, but in which the considered value is coalitional rational. For the Shapley Value, in technical words, in the Inverse Set relative to the given Shapley Value, find out a TU game for which this Shapley Value is coalitional rational.

In the present paper, the similar problem is now considered for the Banzhaf Value and the Semivalues, (values introduced in [4] [5] , respectively). These values are usually non-efficient, so that they will not be in the Core; therefore we have to define now what it is a coalitional rational Banzhaf Value, and more general a Semivalue. The main idea will be that of going on the path met in a previous joint work [6] .

Precisely, for each game, we associate a Power Game, relative to the Semivalue, and the value of the original game, efficient in the Power Game, is coalitional rational, if it belongs to the Core of the Power Game, called the Power Core. If the Semivalue happens also to be an efficient one, for the original game, then the Power Game is the game itself, so that the new definition of the coalitional rationality should be extending the definition given above for the efficient values. Note that, on the other hand, the Semivalue of the original game is always efficient in the Power Game, hence in the general case we should discuss only the coalitional rationality. An example with some details will be given for a Banzhaf Value, which is efficient for a particular game.

In the following, the concept of Semivalue as well as the solution of the Inverse Problem for Semivalues, will be sketched in the second section. The concept of Power Game and the solution of the above new problem connected to coalitional rationality will be shown in the third section, where several three person games will also illustrate the results, for some non-efficient Semivalues, defined by a priori given weight vectors.

More remarks, about the efficient values, and the computational means for finding solutions of the problem, will be shown in the last section.

2. The Inverse Set for Semivalues

The set of all cooperative TU games, on a finite set of player N, with two operations, addition and scalar multiplication, is a linear vector space, to be denoted by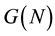, with a dimension of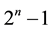. In this space of games, the Semivalue of a game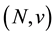, denoted by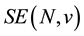, will be defined by a weight vector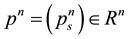, satisfying some condition of normalization, precisely

(1)

The Semivalue may be extended to the sets of games in that contain among others the subgames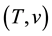, of the game, obtained by restricting this game to the player sets 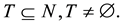For the games in such spaces, one defines the restrictions of the weight vector 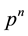to the weight vectors 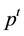obtained by means of what we call the inverse Pascal triangle property: starting from the given weight vector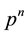, let the weight vectors 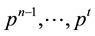be already defined by the formulas

(2)

for and use (2) to define, up to. We see that all weight vectors satisfy normalization conditions similar to (1). The union of all spaces is denoted by. On this set, including the subgames of, the Semivalue defined by the given weight vectors and those derived in (2) is expressed as

(3)

Among the Semivalues, we have the popular particular cases of the Banzhaf Value, obtained for the weight vectors, where we have the components and the Shapley Value where the components of the weight vectors are

(4)

together with the weight vectors derived by means of (2).

The first is usually non-efficient, while the second is always efficient. We mean that the Banzhaf Value may be efficient for some games and non-efficient for others, while the Shapley Value is efficient for all games. An example showing the first situation follows.

Example 1: a) Consider the game

(5)

By computing the Banzhaf Value via formula (3), with the weight vector, and the Shapley Value with the weight vector, we get so that we may check that both are efficient and coalitional rational.

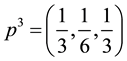
It happened that the two values are equal, a fact discussed in [7] .

For those Semivalues which are efficient, only in the case of some games, there is no need to define again the coalitional rationality.

b) The fact that this may not happen is shown by the game

(6)

for the Banzhaf Value, which is a particular Semivalue. With the same weight vector, we find

, and this is not efficient, because the sum makes, while the coalitional ratio-

nality conditions are satisfied. Clearly, we have to discuss also the coalitional rationality for non-efficient Semivalues.

c) The most general case is the one when for some game and some value, both the efficiency and the coalitional rationality conditions do not hold. For example, if we take for the same game (6) the Semivalue defined

by the weight vector, which satisfies the condition (1), then from formula (3), we obtain

Now, neither the efficiency, nor the coalitional rationality conditions are holding, because the sum of payoffs

makes, and

does not hold; in other words, the last situation is the general case.

Note that in (6) the Shapley Value is which is efficient and coalitional rational. Note the fourth situation, the well known fact that efficient Semivalues equal the Shapley Value, but this may be, or not, coalitional rational; the first case was met above.

Return to the set of games, the union of the vector spaces Consider a game, and compute the Semivalue, by formula (3), for a weight vector, satisfying the normalization condition (1). Let us have. where.

The Inverse Problem for Semivalues, discussed in [2] , can be stated as follows: find out all TU games in the space for which the Semivalue associated with the weight vector, equals L. This problem has already been solved in the above mentioned work of the author, and we shall sketch the solution, before going to the related problem of coalitional rationality. In the space, denote a basis

(7)

defined by means of the formulas

(8)

and otherwise. Note, that the denominators are obtained from the weight vector via the inverse Pascal triangle relationships (2). It is easy to see that these are linearly independent vectors and the set W has the cardinality, hence this is a basis of the space. Thus, any TU game has an expansion

(9)

for some values of the constant coefficients. In the earlier work, it has been shown the following auxiliary results:

(10)

These equalities, as well as the linearity of the Semivalues, shown by formula (3), give so that from (9) we obtain

(11)

In [2] , it has been proved that this is the general solution of the Inverse Problem for the considered Semivalue, that is it is offering an explicit expression for the games in the Inverse Set. Note also from (10) that the parenthesis in (11) has a null Semivalue, hence a basis of the null subspace is also shown in (11), namely

(12)

with dimension Now, a new problem to be discussed in this paper will be introduced, starting with the concept of Power Game, to be used in connection with the coalitional rationality.

3. The Power Game of the Inverse Set and the Coalitional Rationality

For any game, and any value defined on,the Power Game of is the game, derived from the given game by

(13)

Formula (13) shows a nice interpretation of the Power Game: for each coalition in the original game, the worth of the coalition in the Power Game equals the total win of its members, when they use the value. Thus, for a Semivalue, that is if then, by (13), the Semivalue of the original game is efficient in any subgame of the Power Game. The Core of the Power Game is called the Power Core. Now, the natural approach in discussing how to share fairly the total win of the grand coalition in the given game is that of following the ideas introduced in the earlier paper [6] : we shall consider the Semivalue of the given game as efficient and coalitional rational, if it belongs to the Power Core. Hence, to check whether, or not, this happens, we should compute the Power Core.

However, it will be easier to use a computational formula for the Power Core proved also in the same paper [2] ; this will be done next, because we shall compute only the worth of coalitions of size. The problem similar to the one discussed above may be stated as: for a given game, find out a game, with the Semivalue, but in which the Semivalue of the given game is also efficient and coalitional rational. Now, there are two cases: either the Semivalue is in the Core of the Power Game for the given game, or not. In the first case, the Semivalue is considered coalitional rational; in the other case, from we build a new game in the Inverse Set, where this happens. In the following, we shall confine ourselves to a solution in the subfamily of the Inverse Set, to be called the null subfamily. In other words, if the Semivalue is not in the Core of the Power Game of the initial game, then for this game, we want the Semivalue of this given game to belong to the Core of the new game, from the almost null subfamily.

Now, an arbitrary game in the almost null subfamily of the Inverse Set, relative to the Semivalue, is given by

(14)

and depends on the parameter. From (14) and (8), as all the characteristic functions of the basic games are null when, we get For, from (14) and (8),we get

(15)’

Similarly we obtain

(15)”

As noticed above, this game belongs to the almost null subfamily of Inverse Set, for any value of the parameter, and we may check that the Semivalue of any game in this family equals the Semivalue of the original game. From (15), based upon the definition (13), we can compute the Power Game of, denoted, and its Core.

Instead, the Power Game of may be easier computed by using the formula from the previous work mentioned above, precisely

(16)

For,from (8) and (16) we get

(17)

and the efficiency is holding, because we have also

(18)

In this way, we almost proved the following main result:

Theorem: Suppose that the Semivalue, associated with a given weight vector, is. Then, in a game belonging to the subfamily of the Inverse Set relative to the Semivalue, defined by

(19)

the Semivalue is in the Power Core, if and only if the parameter satisfies the inequality

(20)

where the minimum is taken over the index.

Proof: Taking into account the above formulas (17), (18), for the Power Game, the Power Core is given by, and

(21)

from which the result (20) follows, as the efficiency is obvious. ■

Note that the inequality (20) does not depend on the weight vector and it is the same as in [2] , the case of the Shapley Value and other efficient values. This is not surprising, because this theorem is also applicable to the Shapley Value, as the Shapley Value is a particular Semivalue. Other remarks will be discussed later, for the moment let us illustrate the results contained in the theorem.

Example 2: Consider the same three person game of Example 1a, shown in (5). Compute the Semivalue asso-

ciated with the weight vector. From formula (3), we get

(22)

Obviously, the conditions hold, but the Semivalue is not efficient, because this sum

makes 1000; hence, it does not belong to the Core, even though the coaltional rationality conditions hold. Compute the characteristic function for all the coalitions of size two in an arbitrary game belonging to the almost null subfamily of the Inverse Set, relative to the Semivalue and to the vector shown in formula (22), by using the formulas (15). We get

(23)

We may check that the Semivalue of this game is the same as the one in the original game, for whatever value of the parameter The inequality which gives the coalitional rationality, that is (20), is

(24)

where the Semivalue denoted by L, is provided by (22). We have

(25)

By taking for example in formulas (23), we get the game

(26)

where the null worth of the singletons have been omitted. We may check that the Semivalue equals L, and it belongs to the Core of the Power Game for, which is, with

(27)

It follows that the Semivalue of the original game and of the game in the almost null family (26) are coalitional rational as it is in the Core of (27), Hence, the game (26) is a solution for our problem, that is the Semivalue of the original game is coalitional rational, in the above introduced sense. In the next section we shall consider a Semivalue, corresponding to another weight vector, for which neither the efficiency, nor the coalitional rationality will hold, in the original game.

4. Discussion

The following remarks are appropriate:

a) Note that the Semivalue of the Power Game (27) is

(28)

not the same as the Semivalue (22), as the Power Game is not in the almost null subfamily of the Inverse Set. Moreover, it does not belong to the Power Core, as it is not efficient, to be easily checked.

b) It is well known that the Semivalues are efficient if and only if they are Shapley Values. Hence, the above theory applies also to the Shapley Value. However, due to the efficiency the Power Game is the game itself, so that after getting the game belonging to the almost null family, we should get the coalitional rationality condi-

tion from this game. Indeed, looking at the games (15), and using the fact that, from (15) we get

(17), and from here we obtain (20), which gives the same coalitional rationality condition as in the study of coalitional rationality for efficient values (see [3] ).

c) The above results may be applied to the Banzhaf Value, which is a Semivalue defined by the weights The game from the almost null inverse set relative to the Banzhaf Value, with these weight vectors and the value L, is derived from formulas (15) by an easy computation:

(29)

Returning to the game in our example 1, where the Banzhaf Value is

(30)

that happens to be efficient, and if the parameter is chosen to satisfy (20) with equal sign, , we get and

(31)

The Power Game for (31) is

(32)

derived from (15), the Banzhaf Value of original game and the value of the parameter, chosen to satisfy the coalitional rationality. We may check that the Banzhaf Value of the original game belongs to the Core of (32), hence it is coalitional rational.

Example 3. Consider the game (6) of example 1c, and the Semivalue with the weight vector, given by. As already noticed, this is neither efficient, nor coalitional rational. Let us apply the

result of the above Theorem. We may check that this Semivalue is neither efficient, nor coalitional rational.

From formula (20) we see that the Semivalue will be coalitional rational if we have; we may compute from (11) the value of, which means that the Semivalue is not coalitional rational, as it does not

satisfy the above inequality. Now, find out a game in the almost null subset of the Inverse Set, from formula (15),

where we take.

This game is

(33)

From formulas (17), (18), we compute the Power Game and we obtain the game

(34)

We see that the Semivalue is efficient in the Power Game (34) of the Game (33) and we check easily that it is also coalitional rational; hence (33) is the solution of our problem.

d) An interesting case is the case of the Binomial Semivalues, a class of Semivalues introduced in [8] , and discussed in [9] .

5. Conclusion

The present work is a continuation of our earlier work [2] , on the Inverse Problem of Semivalues. By discussing the new problem of the game with the same value, but coalitional rational, we believe that we give also a motivation for the concept of Inverse Set. We introduced this new problem and we offered an explicit numerical procedure for solving the problem, as seen in the examples that are following the theory given above. A nice introduction is the case of efficient values considered in [3] , as well as the application to the case of Binomial Semivalues shown in [9] .

Cite this paper

IrinelDragan, (2015) On the Coalitional Rationality of the Banzhaf Value and Other Non-Efficient Semivalues. Applied Mathematics,06,2069-2076. doi: 10.4236/am.2015.612182

References