Received 6 September 2015; accepted 26 October 2015; published 29 October 2015

ABSTRACT

Nowadays, identification, ranking criteria and location of services are important in the planning and designing of city. In fact, it helps the authorities and managers make better decisions in selecting the best locations to establish urban service centers. The issue of access to urban services is kind of important issue that affects various dimensions of the city. Laboratory service is an example of this kind that the necessity of access to them is crucial for everyone. Decision making to locate the lab is not only necessary in terms of services and costs to users but also, it is essential in the development of city and the spatial distribution pattern of demand. In this paper, the goal was to determine laboratories location using Euclidean square and fuzzy logic, by two different methods to examine and desirable locations for future planning. Also, selected locations for laboratories are significant considering the improvement of service and reducing the cost and time of access to public.

Keywords:

Location Allocation, Fuzzy Logic, Triangular Fuzzy Numbers, Euclidean Square

1. Introduction

Facility location-allocation (FLA), which has been proved to be a valuable method in siting service facility, is widely used in real life, such as emergency service systems, telecommunication net works, public services, etc. Many researchers have studied the FLA problem in a deterministic, stochastic or fuzzy environment [1] . Location of the facilities providing public health service is very crucial in ensuring that the chosen location network serves the purpose of minimizing social cost or equivalently maximizing the benefits of the people. Similarly the demand allocation to these facilities has a direct impact on the whole system’s efficiency [2] .

The strategic planning of a hospital and laboratories network involves long term decisions like facility location and capacity relocation, with these decisions needing to be robust so as to face future changes in demand and supply patterns. In particular, decisions related to the location of new hospitals are especially sensitive since they are hardly reversible (due to the high investments involved) and commonly have political impacts. Furthermore, long term decisions need to consider an evolving environment where uncertainty increases as the planning horizon moves forward. On one hand, the most important decisions are made in the near future, and these decisions need to be made without completely foreseeing the future conditions of the system. On the other hand, decisions made in the distant future can be postponed and revaluated when more information is available (Daskin, Hopp, and Medina 1992). Therefore, the use of a planning horizon is a model feature not only relevant to assist hospital planning, but also to ensure that decisions account for future prospects and do not restrict upcoming choices. Additionally, when planning health systems, decision makers need to take into account different policy objectives that typically include improving access and minimizing costs. These objectives can often be conflicting since improved geographical access may require smaller hospital facilities closer to the populations, which can lead to higher inefficiencies and costs. Thus, alternative solutions which balance these two, often conflicting, objectives are relevant in hospital network planning, especially in the context of systems based on a National Health Service (NHS) structure. Location-allocation models have been used to assist hospital planning, as they allow the simultaneous analysis of decisions as the opening, closing or resizing of facilities, considering the pursuit of multiple objectives.

This study aimed to investigate two models to locate laboratories for hospitals whose goal is to help hospital network planning under uncertainty that come to exist in many real-world applications.

In the first model, we considered some hospitals as available facilities. Two laboratories were considered as new facilities, the goal of which was choosing a proper location to establish two laboratories due to fuzzy relations between the location of available facilities and new facilities. Finally, the resulting system of equations is solved via α-cut and optimized spots of locations with peak performance are selected. In the second state, the model was defined as a model in which the candidate locations are selected and some of them are chosen as the location of establishing new facilities (among the available facilities). The selected spots are triangular fuzzy for solving equations. Then, squared Euclidean distance is considered and solved.

It is also noteworthy that we ignore parameters such as availability, utility, and other criteria that lead the study to MSMD. Therefore, we only considered the parameter of minimizing cost for distance.

2. Literature Review

Fuzzy set theory was initialized by [3] and has been widely applied in many real problems. It has been proved to be a useful tool to solve problems with uncertainty. [1] considers the FLA problem under random fuzzy environment using (α, β)-cost minimization model under the Hurwicz criterion.

[4] present a new model named a-cost model under the Hurwicz criterion with fuzzy demands. [5] defined the facility layout problem as the determination of the relative locations for, and allocation of, the available space among a given number of facilities.

[6] present a model for locating multiple new facilities in convex sets with respect to multiple existing facilities and demand points, then present a linear programming model for this problem with block norms [7] . An approach for computing the positive solution of a fully fuzzy linear system where the coefficient matrix is a fuzzy n × n matrix.

[8] discusses fully fuzzy linear systems with triangular fuzzy numbers. A matrix inversion method is proposed for solving Fully Fuzzy Linear System (FFLS) of equations. [9] devoted to fuzzy linear programming and a model to locate some new facilities among the existing set of facilities. It also gives a convex solution and formulates the model for fuzzy data by an integer linear programming.

The purpose of location-allocation models is to concurrently determine optimal facility locations and the assignment of customers to open facilities (Siddhartha S. Syama, Murray J. Côtéb, 2012). In 1979, England’s Department of Health and Social Security considered strategic development of health care centers. From then on studies in this field started and these studies were followed in Austria during 1980-1982 (Ebrahimzadeh et al., 2009). Location-allocation models have been used as decision support tools for health planning as described by [10] .

Location models have been used as tools to support health planning, with different authors focusing on different systems aspects. Among others, (Narula and Ogbu 1979), (Ruth 1981), (Galvao, Espejo, and Boffey 2002), (Smith et al. 2009), and (Mestre, Oliveira, and Barbosa-Póvoa 2012) have proposed hierarchical models for planning health facilities. Typically, uncertainty in health systems has been essentially addressed with simulation models or queuing theory (see the comprehensive reviews of simulation in healthcare context by (Kat- saliaki and Mustafee 2011) and (Jahangirian et al. 2012); and simulation models for planning health systems by [11] and [12] .

3. Preliminaries

3.1. Fuzzy Logic

A mathematical logic that attempts to solve problems by assigning values to an imprecise spectrum of data in order to arrive at the most accurate conclusion possible. Fuzzy logic is designed to solve problems in the same way that humans do: by considering all available information and making the best possible decision given the input. Logic reflects how people think. It attempts to model our sense of words, our decision making and our common sense [13] .

3.2. Fuzzy Location

Fuzzy locating is a rough but reliable method based on appropriate measuring technology for estimating a location of an object. The concept of precise or crisp locating is replaced with respect to the operational requirements and the economic viability. In most cases the knowledge of exact coordinates does not contribute to operations, but the spatial or planar relation between entities is relevant. Hence fuzzy locating determines the radial distances between entities involved in an operational process and reduces the required accuracy of measurement to basic qualities of close, near or far and to relations simple as in or out. However such segregation shall be achieved with high reliability and sound repetition.

3.3. Triangular Fuzzy Number

Among the various shapes of fuzzy number, triangular fuzzy number (TFN) is the most popular one. Definition (Triangular fuzzy number) it is a fuzzy number represented with three points as follows:

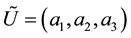
4. Assumptions

1) Coordinate of the existing facilities is definitive.

2) There is a fuzzy relations between the new facilities and existing.

3) In the first case, there is a fuzzy relations between the new facilities.

4) In the second case, there is no relation between the new facilities.

5) Coordinate of the new facilities is definitive.

5. Parameters

i: existing facility index.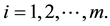

j, k: new facility index. j &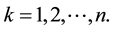

m: the number of the existing facilities.

n: the number of the new facilities.

q: the number of the candidate places.

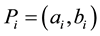: the coordinate of the location of existing facilities.

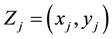: the coordinate of the location of new facilities.

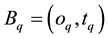: the coordinate of the candidate places.

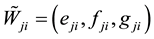: relation weight of transportation between j^th new facility and i^th existing facility.

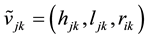: relation weight of transportation between j^th new facility and k^th new facility.

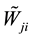and 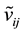are triangular fuzzy number.

C_ji: Annual cost of transportation per unit traveled distance between.

j^th: new facility and i^th existing facility.

S_jk: Annual cost of transportation per unit traveled distance between.

j^th new facility and k^th new facility.

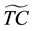: total cost (after calculating the optimal coordinates).

5.1. Decision Variables

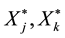: optimum points on the horizontal axis.

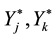: optimum points on the vertical axis.

5.2. Objective Function

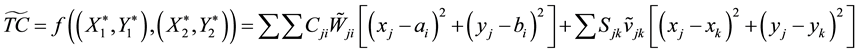
6. Model

Minimize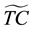

S.t:

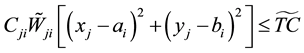
6.1. Case One

In the first model, we consider some hospitals as the existing facilities and two laboratories as the new facilities. The goal of case one is choosing a proper location to establish two laboratories due to fuzzy relations between the location of existing and new facilities. Optimized coordinates will be obtained by using Euclidean square method [14] .

So, the resulting system of equations is solved via α-cut and optimized spots of locations with peak performance which are selected. After placement of the optimal solution in the objective function, the total cost will be obtained.

Solving Matrix Equations

In order to solve the matrix elements of the triangular fuzzy numbers (Ã), α-Cut is used. Then, each component of the matrix turns into interval.

Now if you get crisp interval by α-cut operation, interval A_α shall be obtained as follows ∀α ∈ [0, 1] [3] .

(1.1)

α = 1 in the first stage and second stage put α = 0. Three matrix is solved individually. Finally, we have three amount.

So, using the following equation turns into deterministic value (D):

(1.2)

6.2. Case Two

In this case, the model is defined as a model in which the candidate locations are selected and some of them are chosen as the location of establishing new facilities (among the existing facilities), but there is not a relation between new facilities. The selected spots are triangular fuzzy for solving equations. Then, squared Euclidean distance is considered and solved.

New facilities are independent and equivalent.

We must choose some of these positions.

Three steps are considered in this case:

Step 1: The objective function is calculated for each of the candidate places.

Step 2: The values obtained in Step 1, is sorted in ascending.

Step 3: The results of step 2 have priority in placement of new facilities in candidate places.

7. A Numerical Example

Assume that in a city, there are four hospital. The coordinate of the hospital is given in the Table 1. Due to lack of laboratory near the hospitals, we need to build two labs. This issue is studied in two cases.

7.1. Case One

In order to solve the first case, the values are given in Table 1 and Table 2. So, optimal coordinates are obtained using (1.1). Then, by using the (1.2) they turns into deterministic value.

In this case, fuzzy relation between new facilities is:

After solving the problem, the optimal solution is obtained as follows:

After obtaining coordinates to calculate (=to get on) the objective function the cost of transport between facilities in Table 3 and Table 4, should be multiply to optimized coordinate, finally the total cost is calculated.

After placement of the optimal solution in the objective function, the total cost is obtained as follows:

The cost is obtained due to the lack of candidate locations, which according to the fuzzy relations and methods of Euclidean square is obtained, and in the latter case candidates will be considered.

7.2. Case Two

The objective function will be calculated and the cost will be obtained by using the values given in Tables 5-7. So, the results have priority in placement of new facilities in candidate places.

The cost is calculated for each candidate places. In the end prioritize based on costs obtained.

Priority candidate places are as follows:

8. Result

According to the investigated cases in this article and consideration of future work, it could be concluded that, if the relations between existing facilities and new facilities define as fuzzy relation, possible location for the new facility will be in the different modes as follows:

1) There shouldn’t be candidate places for the new facility, (the choosing the places is optional) and new facilities should be independent of each other (Case one,).

2) There shouldn’t be Candidate places for the new facilities, new facilities shouldn’t be independent of each other and there should be a fuzzy relations between them (Case one,).

3) There should be distinct candidate places for the placement of new facilities and they should be also independent of each other (Case two,).

4) There should be distinct candidate places for the placement of new facilities, they shouldn’t be independent of each other and they should have fuzzy relations (Future work,).

Considering that in most articles, the relation between the new facilities and the existing facilities are considered definitive, the relation between the facilities, in this article, is considered fuzzy, due to be closer to reality. Also in the real world, if you evaluate the extent of the relation between facilities in the location, in the survey of experts, in the end result obtained from the survey, will be as fuzzy.

9. Conclusions and Future Extensions

In this article, Allocation of places to new facilities between existing facilities is studied and the relation between them is a triangular fuzzy relation. In this regard, two views are considered:

In the first case, taking into account that the new facilities are not similar, they have fuzzy relations and their coordinate positions are determined. In the second case for placement of new facilities, the coordinates of the candidate locations are considered and it is assumed that the new facilities are similar to each other. In both cases, the distances between the facilities are calculated by using Euclidean square. An extension to this study is that:

In the second case, the coordinates of the candidate places of the new facility can be considered different (not similar) and dependent. And the new facility can be dissimilar fuzzy relation.

Cite this paper

NasimRad,MohammadrezaRazdar,RoghayyehHeidarizadeh,AbolfazlMirzazadeh, (2015) Location-Allocation in the Two Conditions of Candidate and Non-Candidate Places with Fuzzy Relations between Facilities Using Euclidean Square Method. Applied Mathematics,06,1918-1925. doi: 10.4236/am.2015.611169

References