Received 8 August 2015; accepted 21 September 2015; published 24 September 2015

ABSTRACT

Totally equistable, totally f₀-equistable, practically equistable, and practically f₀-equistable of system of differential equations are studied. Cone valued perturbing Liapunov functions method and comparison methods are used. Some results of these properties are given.

Keywords:

Totally Equistable, Totally f₀-Equistable, Practically Equistable, Practically f₀-Equistable

1. Introduction

Consider the non linear system of ordinary differential equations

(1.1)

and the perturbed system

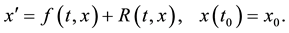(1.2)

Let Rⁿ be Euclidean n-dimensional real space with any convenient norm, and scalar product. Let for some

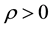
where denotes the space of continuous mappings 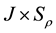into.

Consider the scalar differential equations with an initial condition

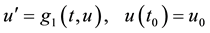, (1.3)

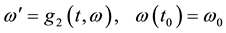(1.4)

and the perturbing equations

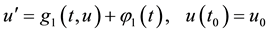(1.5)

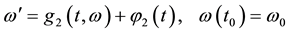(1.6)

where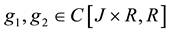, 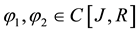respectively.

Other mathematicians have been interested in properties of qualitative theory of nonlinear systems of differential equations. In last decade, in [1] , some different concepts of stability of system of ordinary differential Equations (1.1) are considered namely, say totally stability, practically stability of (1.1), and (1.2); and in [2] , methods of perturbing Liapunov function are used to discuss stability of (1.1). The authors in [3] discussed some stability of system of ordinary differential equations, and in [4] [5] the authors discussed totally and totally φ₀-stability of system of ordinary differential Equations (1.1) using Liapunov function method that was played essential role for determine stability of system of differential equations. In [6] the authors discussed practically stability for system of functional differential equations.

In [7] , and [8] , the authors discussed new concept namely, φ₀-equitable of the zero solution of system of ordinary differential equations using cone-valued Liapunov function method. In [4] , the author discussed and improved some concepts stability and discussed concept mix between totally stability from one side and φ₀- stability on the other side.

In this paper, we will discuss and improve the concept of totally stability, practically stability of the system of ordinary differential Equations (1.1) with Liapunov function method, and comparison technique. Furthermore, we will discuss and improve the concept of totally φ₀-stability, and practically φ₀-stability of the system of ordinary differential Equations (1.1). These concepts are mix and lie somewhere between totally stability and practically stability from one side and φ₀-stability on the other side. Our technique depends on cone-valued Liapunov function method, and comparison technique. Also we give some results of these concepts of the zero solution of differential equations.

The following definitions [8] will be needed in the sequal.

Definition 1.1. A proper subset of is called a cone if

where and denote the closure and interior of K respectively and denotes the boundary of

Definition 1.2. The set is called the adjoint cone if it satisfies the properties of the definition 3.1.

Definition 1.3. A function is called quasimonotone relative to the cone K if

then there exists such that

Definition 1.4. A function is said to belong to the class if and is strictly monotone increasing in r.

2. Totally Equistable

In this section we discuss the concept of totally equistable of the zero solution of (1.1) using perturbing Liapuniv functions method and Comparison principle method.

We define for, the function by

The following definition [1] will be needed in the sequal.

Definition 2.1. The zero solution of the system (1.1) is said to be -totally equistable (stable with respect to permanent perturbations), if for every there exist two positive numbers and such that for every solution of perturbed Equation (1.2), the inequality

holds, provided that and.

Definition 2.2. The zero solution of the Equation (1.3) is said to be -totally equistable (stable with respect to permanent perturbations), if for every, there exist two positive numbers and such that for every solution of perturbed Equation (1.5). The inequality

holds, provided that and.

Theorem 2.1. Suppose that there exist two functions

with

and there exist two Liapunov functions

and with

where for and denotes the complement of satisfying the following con- ditions:

(H₁) is locally Lipschitzian in x.

(H₂) is locally Lipschitzian in x.

where are increasing functions.

(H₃)

(H₄) If the zero solution of (1.3) is equistable, and the zero solution of (1.4) is totally equistable.

Then the zero solution of (1.1) is totally equistable.

Proof. Since the zero solution of the system (1.4) is totally equistable, given, there exist two positive numbers and such that for every solution of perturbed equation (1.6) the inequality

(2.1)

holds, provided that and.

Since the zero solution of (1.3) is equistable given and, there exists such that

(2.2)

holds, provided that

From the condition (H₂) we can find such that

(2.3)

To show that the zero solution of (1.1) is -totally equistable, it must show that for every there exist two positive numbers and such that for every solution of perturbed Equation (1.2). The inequality

holds, provided that and.

Suppose that this is false, then there exists a solution of (1.2) with such that

(2.4)

Let and setting

Since and are Lipschitzian in x for constants and respectively.

Then

where From the condition (H₃) we obtain the differential inequality

for Then we have

Let

Applying the comparison Theorem (1.4.1) of [1] , it yields

where is the maximal solution of the perturbed Equation (1.6).

Define

To prove that

It must be show that

and.

Choose. From the condition (H₁) and applying the comparison Theorem of [1] , it yields

where is the maximal solution of (1.3).

From (2.2) at

(2.5)

From the condition (H₂) and (2.4), at

(2.6)

From (2.3), we get

Since

From (2.1), we get

(2.7)

Then from the condition (H₂), (2.4) and (2.7) we get

This is a contradiction, then it must be

holds, provided that and.

Therefore the zero solution of (1.1) is totally equistable.

3. Totally f₀-Equistable

In this section we discuss the concept of Totally f₀-equistable of the zero solution of (1.1) using cone valued perturbing Liapunov functions method and Comparison principle method.

The following definition [4] will be needed in the sequal.

Definition 3.1. The zero solution of the system (1.1) is said to be totally f₀-equistable (f₀-equistable with respect to permanent perturbations), if for every, and, there exist two positive numbers and such that the inequality

holds, provided that and where is the maximal solution of perturbed Equation (1.2).

Let for some

Theorem 3.1. Suppose that there exist two functions

with

and let there exist two cone valued Liapunov functions

and with

where for and denotes the complement of satisfying the following conditions:

(h₁) is locally Lipschitzian in and

(h₂) is locally Lipschitzian in and

where are increasing functions.

(h₃)

(h₄) If the zero solution of (1.3) is f₀-equistable, and the zero solution of (1.4) is totally f₀-equistable. Then the zero solution of (1.1) is totally f₀-equistable.

Proof. Since the zero solution of (1.4) is totally f₀-equistable, given, given there exist two positive numbers and such that the inequality

(3.1)

holds, provided that and. where is the maximal solution of perturbed Equation (1.6).

Since the zero solution of the system (1.3) is f₀-equistable, given and there exists

such that

(3.2)

holds, provided that where is the maximal solution of (1.3).

From the condition (h₂) we can choose such that

(3.3)

To show that the zero solution of (1.1) is T₁-totally f₀-equistable, it must be prove that for every and there exist two positive numbers and such that the inequality

holds, provided that and where is the maximal solution of perturbed Equation (1.2).

Suppose that is false, then there exists a solution of (1.2) with such that

(3.4)

Let and setting

Since and are Lipschitzian in x for constants and respectively.

Then

where From the condition (h₃) we obtain the differential inequality

for Then we have

Let. Applying the comparison Theorem of [1] , yields

Define

To prove that

It must be shown that

Choose. From the condition (h₁) and applying the comparison Theorem [1] , it yields

From (3.2) at

(3.5)

From the condition (h₂) and (3.4), at

(3.6)

From (3.3), we get

Since

From (3.1), we get

(3.7)

Then from the condition (h₂), (3.4) and (3.7) we get at

This is a contradiction, then

provided that and where is the maximal solution of perturbed equation (1.2). Therefore the zero solution of (1.1) is totally f₀-equistable.

4. Practically Equistable

In this section, we discuss the concept of practically equistable of the zero solution of (1.1) using perturbing Liapunov functions method and Comparison principle method.

The following definition [8] will be needed in the sequal.

Definition 4.1. Let be given. The system (1.1) is said to be practically equistable if for such that the inequality

(4.1)

holds, provided that where is any solution of (1.1).

In case of uniformly practically equistable, the inequality (4.1) holds for any.

We define

.

Theorem 4.1. Suppose that there exist two functions

with

and there exist two Liapunov functions

and with

where and denotes the complement of satisfying the following conditions:

(I) is locally Lipschitzian in x.

(II) is locally Lipschitzian in x.

where are increasing functions.

(III)

(IV) If the zero solution of (1.3) is equistable, and the zero solution of (1.4) is uniformly practically equistable.

Then the zero solution of (1.1) is practically equistable.

Proof. Since the zero solution of (1.4) is uniformly practically equistable, given such that for every solution of (1.4) the inequality

holds provided.

Since the zero solution of the system (1.3) is equistable, given and there exist

such that for every solution of (1.3)

holds provided that.

From the condition (II) we can find such that

To show that the zero solution of (1.1) practically equistable, it must be exist such that for any solution of (1.1) the inequality

holds, provided that.

Suppose that this is false, then there exists a solution of (1.1) with such that

(4.5)

Let and setting

From the condition (III) we obtain the differential inequality for

Let

Applying the comparison Theorem [8] , yields

where is the maximal solution of (1.4).

To prove that

It must be show that.

Choose, from the condition (II) and applying the comparison Theorem of [1] , yields

where is the maximal solution of (1.3).

From (4.3) at

(4.6)

From the condition (II) and (4.5), at

(4.7)

From (4.4), (4.6) and (4.7), we get

From (4.2), we get

(4.8)

Then from the condition (II), (4.5) and (4.8), we get at

This is a contradiction, then

provided that.

Therefore the zero solution of (1.1) is practically equistable.

5. Practically f₀-Equistable

In this section we discuss the concept of practically f₀-equistable of the zero solution of (1.1) using cone valued perturbing Liapunov functions method and comparison principle method.

The following definitions [6] will be needed in the sequal.

Definition 5.1. Let be given. The system (1.1) is said to be practically f₀-equistable, if for and such that the inequality

(5.1)

holds, provided that where is the maximal solution of (1.1).

In case of uniformly practically f₀-equistable, the inequality (5.1) holds for any.

We define

Theorem 5.1. Suppose that there exist two functions

with

and let there exist two cone valued Liapunov functions

and with

where and denotes the complement of satisfying the following conditions:

(i) is locally Lipschitzian in x relative to K.

(ii) is locally Lipschitzian in x relative to K.

where are increasing functions.

(iii)

(iv) If the zero solution of (1.3) is f₀-equistable, and the zero solution of (1.4) is uniformly practically f₀- equistable.

Then the zero solution of (1.1) is practically f₀-equistable.

Proof. Since the zero solution of the system (1.4) is uniformly practically f₀-equistable, given for such that the inequality

(5.2)

holds provided, where is the maximal solution of (1.4).

Since the zero solution of the system (1.3) is f₀-equistable, given and there exist

such that the inequality

(5.3)

From the condition (ii), assume that

(5.4)

also we can choose such that

(5.5)

To show that the zero solution of (1.1) is practically f₀-equistable. It must be show that for and such that the inequality

holds, provided that where is the maximal solution of (1.1).

Suppose that is false, then there exists a solution of (1.1) with such that for where

(5.6)

Let and setting

From the condition (iii) we obtain the differential inequality

Let

Applying the comparison Theorem of [1] , yields

To prove that

It must be show that

Choose From the condition (i) and applying the comparison Theorem of [1] , yield

From (5.3) at

(5.8)

From the condition (ii) and (5.6), at

(5.9)

From (5.5), (5.8) and (5.9), we get

From (5.2), we get

(5.10)

Then from the condition (ii), (5.4), (5.6) and (5.10), we get at

which leads to a contradiction, then it must be

holds, provided that Therefore the zero solution of (1.1) is practically f₀-equistable.

Acknowledgements

The authors would thank referees the manuscript for a valuable corrections of it.

Cite this paper

A. A.Soliman,W. F.Seyam, (2015) On Stability of Nonlinear Differential System via Cone-Perturbing Liapunov Function Method. Applied Mathematics,06,1769-1780. doi: 10.4236/am.2015.610157

References