Applied Mathematics
Vol.06 No.08(2015), Article ID:57977,8 pages
10.4236/am.2015.68117
Application of Hyperbola Function Method to the Family of Third Order Korteweg-de Vries Equations
Luwai Wazzan
Department of Mathematics, King Abdulaziz University, Jeddah, Saudi Arabia
Email: lwazzan@hotmail.com
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 26 May 2015; accepted 12 July 2015; published 16 July 2015
ABSTRACT
In this work, we apply a hyperbola function method to solve the nonlinear family of third order Korteweg-de Vries equations. Exact travelling wave solutions are obtained and expressed in terms of hyperbolic functions and trigonometric functions. The method used is a promising method to solve other nonlinear evaluation equations.
Keywords:
Nonlinear Family of Third Order Korteeweg-de Vries, The Hyperbola Function Method, Ordinary Differential Equations, Hyperbolic Polynomial, Travelling Wave Solutions

1. Introduction
Nonlinear partial differential equations (NLPDEs) have a significant role in several scientific and engineering fields. Since the discovery of soliton in 1965 by Zabusky and Kruskal [1] , many NLPDEs have been derived and extensively applied in different branches of physics and applied mathematics. These equations appear in con- densed matter, solid state physics, fluid mechanics, chemical kinetics, plasma physics, nonlinear optics, propagation of fluxions in Josephson junctions, theory of turbulence, ocean dynamics, biophysics and star formation and many others. In order to understand the different nonlinear phenomena, various methods for obtaining exact solutions to NLPDEs have been proposed. Among these are the inverse scattering method [2] , Hirota’s method [3] , Backlund transformation [4] , F-expansion method [5] , homogeneous balance method [6] , tanh-function method [7] , Jacobi elliptic function method [8] , and many others.
In this project, we consider the nonlinear family of third order Korteweg-de Vries (KdV) equations in [9] of the form
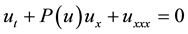 (1)
(1)
where  is a function of space x and time t. The nonlinear term
is a function of space x and time t. The nonlinear term 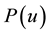 takes the forms
takes the forms
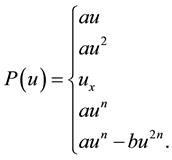 (2)
(2)
For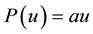 , Equation (1) becomes the standard KdV equation. When
, Equation (1) becomes the standard KdV equation. When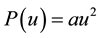 , Equation (1) is called the modified KdV (mKdV) equation [10] . For
, Equation (1) is called the modified KdV (mKdV) equation [10] . For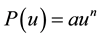 , Equation (1) is called the generalized KdV (gKdV) equation [11] . If
, Equation (1) is called the generalized KdV (gKdV) equation [11] . If  , then Equation (1) is called potential KdV equation. When
, then Equation (1) is called potential KdV equation. When , we get the generalized KdV equation with two power nonlinearities [12] . The KdV equation is used to model the disturbance of the surface of shallow water in the presence of solitary waves. It is a generic model for the study of weakly nonlinear long waves, incorporating leading order nonlinearity and dispersion [13] . The mKdV equation appears in electric circuits and multi-component plasmas [14] . The generalized KdV equation serves as an approximate model for the description of week dispersive effects on the propagation of nonlinear waves characteristic direction [14] . The nonlinear family of third order Korteweg-de Vries equation and other related equations were solved by many methods. For single soliton solutions, the tanh-function method [15] , the tanh- coth method [16] , the modified tanh-coth method [17] -[20] , the sine-cosine method [21] , the inverse scattering method [22] , were used. For the concept of multiple solitons solutions, the Hirota bilinear formalism [23] and a simplified version of this method [24] were used. Our intention in this work is to find new solitary-wave solutions for the nonlinear family of third order Korteeweg-de Vries. Since there is no unified method that can be used to handle all types of nonlinear problems, we will use a hyperbola function method [25] .
, we get the generalized KdV equation with two power nonlinearities [12] . The KdV equation is used to model the disturbance of the surface of shallow water in the presence of solitary waves. It is a generic model for the study of weakly nonlinear long waves, incorporating leading order nonlinearity and dispersion [13] . The mKdV equation appears in electric circuits and multi-component plasmas [14] . The generalized KdV equation serves as an approximate model for the description of week dispersive effects on the propagation of nonlinear waves characteristic direction [14] . The nonlinear family of third order Korteweg-de Vries equation and other related equations were solved by many methods. For single soliton solutions, the tanh-function method [15] , the tanh- coth method [16] , the modified tanh-coth method [17] -[20] , the sine-cosine method [21] , the inverse scattering method [22] , were used. For the concept of multiple solitons solutions, the Hirota bilinear formalism [23] and a simplified version of this method [24] were used. Our intention in this work is to find new solitary-wave solutions for the nonlinear family of third order Korteeweg-de Vries. Since there is no unified method that can be used to handle all types of nonlinear problems, we will use a hyperbola function method [25] .
2. Hyperbola Function Method
We describe this method, for a given nonlinear partial differential equation, say, in two variables,
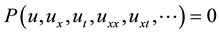 (3)
(3)
Let 
 then Equation (3) reduces to a nonlinear ordinary differential equation (ODE)
then Equation (3) reduces to a nonlinear ordinary differential equation (ODE)
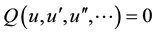 (4)
(4)
We suppose that the solution of the ODE (4) is of the form
 (5)
(5)
where the coefficients 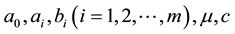 are constants to be determined and
are constants to be determined and 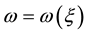 satisfies a nonlinear ordinary differential equation
satisfies a nonlinear ordinary differential equation

Note that, 

and 

The parameter m will be found by balancing the highest-order nonlinear terms with the highest-order partial derivative term in the given equation and then give the formal solution. Substituting the formal solution (5) and transformation (6) into the ordinary differential equation (4) and the change it into hyperbolic polynomial iden- tities for the intermediate variable

the coefficients of the each order of 


to zero, we obtain a set of nonlinear algebraic equations for

2.1. Applications of the Hyperbola Function Method
2.1.1. The KdV Equation

Here we choose 



Balancing the order of the nonlinear term 




Substituting (11) in (10) and using

・
・
・
・
・
・
For 
For

2.1.2. The mKdV Equation

Here we choose 



Balancing the order of the nonlinear term 




Substituting (14) in (13) and using

・
・
・
・
・
・
For 
For
For

2.1.3. The pKdV Equation

Here we choose 



Balancing the order of the nonlinear term 




Substituting (17) in (16) and using

・
・
・
・
・
・
For 
For


2.1.4. The gKdV Equation

Here we choose 



Balancing the order of the nonlinear term 


gives 

Substituting (20) in (19) we get

Balancing the order of 




Substituting (22) in (21) and using

・
・
・
For 
For


3. Conclusion
In this article, the hyperbola function method has been successfully implemented to find new traveling wave solutions for the nonlinear family of third order Korteweg-de Vries. The results show that this method is a powerful Mathematical tool for obtaining exact solutions for the nonlinear family of third KdV. It is also a promising method to solve other nonlinear partial differential equations.
Acknowledgements
This project was founded by the Deanship of Scientific Research (DSR), King Abdualaziz University, Jeddah, under grant No. (429/091-3). The authors, therefore, acknowledge with thanks DSR technical and financial support.
Cite this paper
LuwaiWazzan, (2015) Application of Hyperbola Function Method to the Family of Third Order Korteweg-de Vries Equations. Applied Mathematics,06,1241-1249. doi: 10.4236/am.2015.68117
References
- 1. Zabusky, N.J. and Kruskal, M.D. (1965) Interaction of “Solitons” in a Collisionless Plasma and the Recurrence of Initial States. Physical Review Letters, 15, 240.
http://dx.doi.org/10.1103/PhysRevLett.15.240 - 2. Ablowitz, M.J. and Clarkson, P.A. (1992) Solitons, Nonlinear Evolution Equations and Inverse Scattering. Cambridge University Press, Cambridge.
- 3. Hirota, R. (1973) Exact N-Soliton Solutions of the Wave Equation of Long Waves in Shallow-Water and in Nonlinear Lattices. Journal of Mathematical Physics, 14, 810.
http://dx.doi.org/10.1063/1.1666400 - 4. Wadati, M. (1975) Wave Propagation in Nonlinear Lattice. II. Journal of the Physical Society of Japan, 38, 681.
http://dx.doi.org/10.1143/JPSJ.38.681 - 5. Wang, M. and Li, X. (2005) Extended F-Expansion Method and Periodic Wave Solutions for the Generalized Zakharov Equations. Physics Letters A, 343, 48.
http://dx.doi.org/10.1016/j.physleta.2005.05.085 - 6. Fan, F. (2000) Two New Applications of the Homogeneous Balance Method. Physics Letters A, 265, 353.
http://dx.doi.org/10.1016/S0375-9601(00)00010-4 - 7. Lan, H. and Wang, K. (1990) Exact Solutions for Two Nonlinear Equations I. Journal of Physics A: Mathematical and General, 23, 3923.
http://dx.doi.org/10.1088/0305-4470/23/17/021 - 8. Yan, Z. (2003) Symbolic Computation and Weierstrass Elliptic Function Solution of The Davey—Stewartson (DS) System. International Journal of Modern Physics C, 14, 1127.
http://dx.doi.org/10.1142/S0129183103005224 - 9. Korteweg, D.J. and de Vries, G. (1895) On the Change of Form of Long Waves Advancing in a Rectangular Canal and on a New Type of Long Stationary Waves. Philosophical Magazine, 36, 422-443.
http://dx.doi.org/10.1080/14786449508620739 - 10. Schamel, H. (1973) A Modified Korteweg-de Vries Equation for Ion Acoustic Wavess Due to Resonant Electrons. Journal of Plasma Physics, 9, 377-387.
http://dx.doi.org/10.1017/S002237780000756X - 11. Drazin, P.G. and Johnson, R.S. (1996) Solitons: An Introduction. Cambridge University Press, Cambridge.
- 12. Whitham, G.B. (1999) Linear and Nonlinear Waves. Wiley-Interscience, New York.
http://dx.doi.org/10.1002/9781118032954 - 13. Marchant, T.R. and Smyth, N.F. (1996) Soliton Interaction for the Extended Korteweg-De Vries Equation. IMA Journal of Applied Mathematics, 56, 157-176.
http://dx.doi.org/10.1093/imamat/56.2.157 - 14. Wazwaz, A.-M. (2008) Chapter 9: The KdV Equation. In: Dafermos, C.M. and Pokorny, M., Eds., Handbook of Differential Equations: Evolutionary Equations, Volume 4, Elsevier, Amsterdam, 485-568.
- 15. Malfliet, W. (1992) Solitary Wave Solutions of Nonlinear Wave Equations. American Journal of Physics, 60, 650-654.
http://dx.doi.org/10.1119/1.17120 - 16. Wazwaz, A.M. (2007) The Extended Tanh Method for New Solitons Solutions for Many Forms of the Fifth-Order KdV Equations. Applied Mathematics and Computation, 184, 1002-1014.
http://dx.doi.org/10.1016/j.amc.2006.07.002 - 17. El-Wakil, S.A., El-labany, S.K., Zahran, M.A. and Sabry, R. (2005) Modified Extended Tanh-Function Method and Its Applications to Nonlinear Equations. Applied Mathematics and Computation, 161, 403-412.
http://dx.doi.org/10.1016/j.amc.2003.12.035 - 18. El-Wakil, S.A., El-labany, S.K., Zahran, M.A. and Sabry, R. (2002) Modified Extended Tanh-Function Method for Solving Nonlinear Partial Differential Equations. Physics Letters A, 299, 179-188.
http://dx.doi.org/10.1016/S0375-9601(02)00669-2 - 19. Wazzan, L. (2009) A Modified Tanh—Coth Method for Solving the KdV and the KdV—Burgers’ Equations. Communications in Nonlinear Science and Numerical Simulation, 14, 443-450.
http://dx.doi.org/10.1016/j.cnsns.2007.06.011 - 20. Wazzan, L. (2009) A Modified Tanh—Coth Method for Solving the General Burgers—Fisher and the Kuramoto— Sivashinsky Equations. Communications in Nonlinear Science and Numerical Simulation, 14, 2642-2652.
http://dx.doi.org/10.1016/j.cnsns.2008.08.004 - 21. Wazwaz, A.M. (2002) Partial Differential Equations: Methods and Applications. Balkema Publishers, Leiden.
- 22. Ablowitz, M.J. and Clarkson, P.A. (1991) Solitons, Nonlinear Evolution Equations and Inverse Scattering. Cambridge University Press, Cambridge.
http://dx.doi.org/10.1017/CBO9780511623998 - 23. Hirota, R. (2004) The Direct Method in Soliton Theory. Cambridge University Press, Cambridge.
http://dx.doi.org/10.1017/CBO9780511543043 - 24. Hereman, W. and Zhuang, W. (1980) Symbolic Software for Soliton Theory. Acta Applicandae Mathematica, 39, 361-378.
- 25. Bai, C.-L. (2001) Exact Solutions for Nonlinear Partial Differential Equation: A New Approach. Physics Letters A, 288, 191-195.
http://dx.doi.org/10.1016/S0375-9601(01)00522-9










































































