Applied Mathematics
Vol.06 No.05(2015), Article ID:56415,9 pages
10.4236/am.2015.65078
Approximate Technique for Solving Class of Fractional Variational Problems
Emad M. Solouma1,2, Mohamed M. Khader1,3
1Department of Mathematics and Statistics, College of Science, Al-Imam Mohammad Ibn Saud Islamic, University (IMSIU), Riyadh, Saudi Arabia
2Department of Mathematics, College of Science, Beni-Suef University, Beni-Suef, Egypt
3Department of Mathematics, Faculty of Science, Benha University, Benha, Egypt
Email: emadms74@gmail.com, mohamedmbd@yahoo.com, mohamed.khader@fsc.bu.edu.eg
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 20 April 2015; accepted 16 May 2015; published 19 May 2015
ABSTRACT
This paper is devoted to implementing the Legendre spectral collocation method to introduce numerical solutions of a certain class of fractional variational problems (FVPs). The properties of the Legendre polynomials and Rayleigh-Ritz method are used to reduce the FVPs to the solution of system of algebraic equations. Also, we study the convergence analysis. The obtained numerical results show the simplicity and the efficiency of the proposed method.
Keywords:
Fractional Variational Problems, Caputo Fractional Derivatives, Legendre Spectral Collocation Method, Rayleigh-Ritz Method, Convergence Analysis

1. Introduction
Fractional derivatives have recently played a significant role in many areas of sciences, engineering, fluid mechanics, biology, physics and economies. Fractional variational problem is a variational problem in which the performance index or the objective functional contains at least one Caputo fractional derivative. The fractional Euler-Lagrange equation has been used to formulate fractional variational problems [1] . The calculus of variations has a long history and it has been used almost in every field where energy principles are applicable [2] [3] . In a large number of problems arising in analysis, mechanics, geometry, and so forth, it is necessary to determine the maximal and minimal of a certain functional. Because of the important role of this subject in science and engineering, considerable attention has been received on this kind of problems. There are some problems that have an important role in the development of the calculus of variations [4] .
Agrawal [5] presented a heuristic approach to obtain differential equations of fractionally damped systems. Later, Agrawal combined the calculus of variations and the concept of fractional derivatives to develop Euler- Lagrange equations for FVPs [1] . Also, a general finite element formulation for a class of FVPs is presented in [2] , where the fractional derivative is defined in the Riemann-Liouville sense. Finally, Lotfi and Yousefi [6] introduced a numerical method for solving a class of FVPs with multiple dependent variables, and multi order fractional derivatives. They reduced the given optimization problem to a system of algebraic equations using polynomial basis functions. For more details about the historical comments for the variational problems, see [7] [8] .
Spectral collocation methods are efficient and highly accurate techniques for numerical solution of non-linear fractional differential equations (FDEs). The basic idea of the spectral collocation methods is to assume that the unknown solution  can be approximated by a linear combination of some basis functions, called the trial functions, such as orthogonal polynomials. Legendre polynomials are well known family of orthogonal poly- nomials on the interval
can be approximated by a linear combination of some basis functions, called the trial functions, such as orthogonal polynomials. Legendre polynomials are well known family of orthogonal poly- nomials on the interval  that have many applications [9] - [15] . They are widely used because of their good properties in the approximation of functions. We use the Legendre collocation method to discretize FDEs to get linear or non-linear system of algebraic equations, thus greatly simplifying the proposed problem. Recently, the shifted Legendre polynomials have been used as basis functions of numerical techniques for solving types of fractional optimal control problems, see [16] [17] . Legendre expansion method for solving fractional-order de- lay differential equations is given in [18] . Also, many numerical algorithms for calculating the fractional integral and the Caputo derivative are presented in [19] .
that have many applications [9] - [15] . They are widely used because of their good properties in the approximation of functions. We use the Legendre collocation method to discretize FDEs to get linear or non-linear system of algebraic equations, thus greatly simplifying the proposed problem. Recently, the shifted Legendre polynomials have been used as basis functions of numerical techniques for solving types of fractional optimal control problems, see [16] [17] . Legendre expansion method for solving fractional-order de- lay differential equations is given in [18] . Also, many numerical algorithms for calculating the fractional integral and the Caputo derivative are presented in [19] .
In general, we know that it is difficult to find the exact solution of FDEs, so, approximate and numerical methods are used to obtain the numerical solution [20] - [27] . The main aim of the presented paper is concerned with extension of the application of Legendre spectral method to obtain the numerical solution of FVPs. Also, we give and prove an error upper bound of the approximate formula of the fractional derivative and study the convergence analysis.
This paper is organized as follows. We present few preliminaries for Caputo fractional derivatives and some facts about shifted Legendre polynomials in Section 2. In Section 3, we study the error analysis of the introduced approximate formula. In Section 4, we give the procedure of the solution using the proposed method. In Section 5, we introduce some numerical examples. Finally, some concluding remarks are given in the last section.
2. Preliminaries
In this section, we present some necessary definitions and mathematical preliminaries of the fractional calculus theory that will be required in the present paper.
Definition 1
The Caputo fractional derivative operator 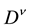 of order
of order 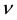 is defined in the following form [28]
is defined in the following form [28]
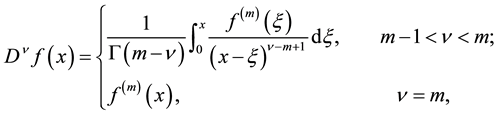
where 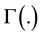 is Gamma function,
is Gamma function, 
For the Caputo’s derivative we have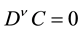 , C is a constant, and
, C is a constant, and
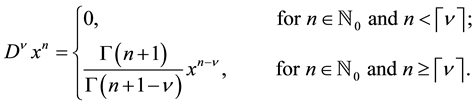 (1)
(1)
We use the ceiling function 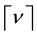 to denote the smallest integer greater than or equal to v and
to denote the smallest integer greater than or equal to v and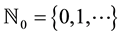 . Recall that for
. Recall that for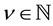 , the Caputo differential operator coincides with the usual differential operator of integer order. For more details on fractional derivatives definitions and its properties see [28] [29] .
, the Caputo differential operator coincides with the usual differential operator of integer order. For more details on fractional derivatives definitions and its properties see [28] [29] .
The well known Legendre polynomials are defined on the interval 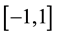 and can be determined with the aid of the following recurrence formula [14]
and can be determined with the aid of the following recurrence formula [14]
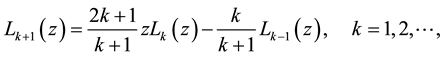
where 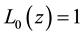 and
and . In order to use these polynomials on the interval
. In order to use these polynomials on the interval 




The analytic form of the shifted Legendre polynomials 

The function


where the coefficients 
In practice, only the first 

The main approximate formula of the fractional derivative is given in the following theorem.
Theorem 1 [23]
Let 


3. Error Analysis
In this section, special attention is given to study the convergence analysis and evaluate an upper bound of the error for the proposed approximate formula.
Theorem 2 [23]
The Caputo fractional derivative of order 

where

Lemma 1 [23]
For any continuous function 




Theorem 3
For a function
1) 

2) 


Then its shifted Legendre approximation 

Proof. Using the properties of the shifted Legendre polynomials, the orthogonal condition and the proved formula (8), we can get
this implies and proves the required relation (9).
Theorem 4 [23]
The error 



4. Procedure Solution for FVPs
In this section, we give a numerical algorithm using Legendre spectral collocation method for obtaining the extremal values of functionals of the general form

subject to boundary conditions

To develop the formulation for the general form (11), we follow the following steps:
1) Approximate the function 


where 
2) Use the trapezoidal integration technique to compute the integral term in Equation (13) as in the following approximated formula

where

3) The extremal values of functionals of the general form (14), according to Rayleigh-Ritz method gives
which represent 



4) Solve the algebraic system to obtain

5. Numerical Examples
In this section, to demonstrate the performance of the computational procedure developed above, we present numerical results of three different examples.
Problem 1 [2]
Consider the following FVP: Find the extremum of the functional

under the following boundary conditions

In order to use the Legendre collocation method, we approximate 


To obtain the numerical solution of the proposed problem (15) we follow the following steps:
1) Substitute the approximation of the function 


where 
2) Use the trapezoidal integration technique to compute the integral term in Equation (18) as in the following approximated formula

where

3) The extremal values of functionals of the general form (19), according to Rayleigh-Ritz method gives

also, using the boundary conditions (16) with respect to (17) and using 


So, from Equations (20) and (21), we obtain a system of 4 algebraic equations in the unknowns c0, c1, c2 and c3.
4) Solve the resulting algebraic system to obtain c0, c1, c2 and c3, then the function 
The behavior of the numerical solutions of this problem with different values of N and 






From these figures, we can conclude that the numerical results obtained by using the proposed method are in excellent agreement with the exact solution and the numerical results obtained using the general finite element formulation [2] .
Problem 2 [2]
Consider the following FVP: Find the extremum of the functional

under the following boundary conditions
The behavior of the numerical solution of this problem with different values of N and 





From Figure 3 and Figure 4, we can conclude that the numerical results obtained by using the proposed method are in excellent agreement with the exact solution and the numerical results obtained using the general finite element formulation [2] .
Problem 3 [6]
Consider the following system of FVPs: Find the extremum of the functional

where
Figure 1. The behavior of 


Figure 2. The behavior of 


Figure 3. The behavior of 


Figure 4. The behavior of 

under the following boundary conditions

For the given problem we have 


The behavior of the numerical and exact solutions of this problem with different values of 

6. Conclusion and Remarks
In the presented study, Legendre spectral method has been successfully used to obtain the numerical solutions of fractional variational problems. In these equations, the fractional derivative is considered in the Caputo form. The fractional derivative is approximated by means of the same formula derived in [18] . The properties of the Legendre polynomials and Rayleigh-Ritz method are used to reduce the proposed problem to the solution of system of algebraic equations. Also, the additional contribution in this paper is given to study the convergence analysis and deduce an error upper bound of the proposed method. One can easily conclude from the presented results that the proposed method is a highly good one to obtain numerical solutions of this kind of fractional variational equations. It is evident that the overall errors can be made smaller by adding new terms from the series (17). Comparison is made between the obtained approximate solution and the exact solution with other methods to illustrate the validity and the great potential of the proposed technique. All computations in this paper are done using Matlab 8.
Figure 5. The behavior of 


Acknowledgements
We thank the Editor and the referee for their comments.
References
- Agrawal, O.P. (2002) Formulation of Euler-Lagrange Equations for Fractional Variational Problems. Journal of Mathematical Analysis and Application, 272, 368-379. http://dx.doi.org/10.1016/S0022-247X(02)00180-4
- Agrawal, O.P. (2008) A General Finite Element Formulation for Fractional Variational Problems. Journal of Mathematical Analysis and Application, 337, 1-12. http://dx.doi.org/10.1016/j.jmaa.2007.03.105
- Dehghan, M. and Tatari, M. (2006) The Use of Adomian Decomposition Method for Solving Problems in Calculus of Variations. Mathematical Problems in Engineering, 2006, 12 p. http://dx.doi.org/10.1155/MPE/2006/65379
- Elsgolts, L. (1977) Differential Equations and the Calculus of Variations. Translated from the Russian by G. Yankovsky, Mir, Moscow.
- Agrawal, O.P. (2001) A New Lagrangian and a New Lagrange Equation of Motion for Fractionally Damped Systems. Journal of Applied Mechanics, 68, 339-341. http://dx.doi.org/10.1115/1.1352017
- Lotfi, A. and Yousefi, S.A. (2013) A Numerical Technique for Solving a Class of Fractional Variational Problems. Journal of Computational and Applied Mathematics, 237, 633-643. http://dx.doi.org/10.1016/j.cam.2012.08.005
- Atanackovi
, T.M., Konjik, S., Pilipovi
, T.M., Konjik, S., Pilipovi
, S. and Simi
, S. and Simi
, S. (2009) Variational Problems with Fractional Derivatives: Invariance Conditions and Nöther’s Theorem. Nonlinear Analysis: Theory, Methods & Applications, 71, 1504-1517. >http://html.scirp.org/file/10-7402723x140.png" class="200" />, S. (2009) Variational Problems with Fractional Derivatives: Invariance Conditions and Nöther’s Theorem. Nonlinear Analysis: Theory, Methods & Applications, 71, 1504-1517. http://dx.doi.org/10.1016/j.na.2008.12.043
- Gelfand, I.M. and Fomin, S.V. (1963) Calculus of Variations. Revised English Edition Translated and Edited by R. A. Silverman, Prentice-Hall, New Jersey.
- Doha, E.H., Bhrawy, A.H. and Ezz-Eldien, S.S. (2011) Efficient Chebyshev Spectral Methods for Solving Multi-Term Fractional Orders Differential Equations. Applied Mathematical Modelling, 35, 5662-5672. http://dx.doi.org/10.1016/j.apm.2011.05.011
- Doha, E.H., Bhrawy, A.H. and Ezz-Eldien, S.S. (2015) An Efficient Legendre Spectral Tau Matrix Formulation for Solving Fractional Sub-Diffusion and Reaction Sub-Diffusion Equations. Journal of Computational and Nonlinear Dynamics, 10, Article ID: 021019. http://dx.doi.org/10.1115/1.4027944
- Bhrawy, A.H., Doha, E.H., Ezz-Eldien, S.S. and Abdelkawy, M.A. (2015) A Numerical Technique Based on the Shift- ed Legendre Polynomials for Solving the Time-Fractional Coupled KdV Equation. Calcolo, in press. http://dx.doi.org/10.1007/s10092-014-0132-x
- Bhrawy, A.H. and Abdelkawy, M.A. (2015) A Fully Spectral Collocation Approximation for Multi-Dimensional Fractional Schrödinger Equations. Journal of Computational Physics, 294, 462-483. http://dx.doi.org/10.1016/j.jcp.2015.03.063
- Bhrawy, A.H. and Zaky, M.A. (2015) A Method Based on the Jacobi Tau Approximation for Solving Multi-Term Time-Space Fractional Partial Differential Equations. Journal of Comptuational Physics, 281, 876-895. http://dx.doi.org/10.1016/j.jcp.2014.10.060
- Bell, W.W. (1968) Special Functions for Scientists and Engineers. Butler and Tanner Ltd., Frome.
- Khader, M.M. (2011) On the Numerical Solutions for the Fractional Diffusion Equation. Communications in Nonlinear Science and Numerical Simulation, 16, 2535-2542. http://dx.doi.org/10.1016/j.cnsns.2010.09.007
- Bhrawy, A.H., Doha, E.H., Tenreiro Machado, J.A. and Ezz-Eldien, S.S. (2015) An Efficient Numerical Scheme for Solving Multi-Dimensional Fractional Optimal Control Problems with a Quadratic Performance Index. Asian Journal of Control, in press. http://dx.doi.org/10.1002/asjc.1109
- Bhrawy, A.H., Doha, E.H., Baleanu, D., Ezz-Eldien, S.S. and Abdelkawy, M.A. (2015) An Accurate Numerical Technique for Solving Fractional Optimal Control Problems. Proceedings of the Romanian Academy Series A, 16, 47-54.
- Khader, M.M. and Hendy, A.S. (2012) The Approximate and Exact Solutions of the Fractional-Order Delay Differential Equations Using Legendre Pseudo-Spectral Method. International Journal of Pure and Applied Mathematics, 74, 287-297.
- Li, C.P., Zeng, F.H. and Liu, F.W. (2012) Spectral Approximations to the Fractional Integral and Derivative. Fractional Calculus and Applied Analysis, 15, 383-406. http://dx.doi.org/10.2478/s13540-012-0028-x
- Khader, M.M. (2013) Numerical Treatment for Solving the Perturbed Fractional PDEs Using Hybrid Techniques. Journal of Computational Physics, 250, 565-573. http://dx.doi.org/10.1016/j.jcp.2013.05.032
- Funaro, D. (1992) Polynomial Approximation of Differential Equations. Springer Verlag, New York.
- Khader, M.M. (2013) Numerical Treatment for Solving Fractional Riccati Differential Equation. Journal of the Egyptian Mathematical Society, 21, 32-37. http://dx.doi.org/10.1016/j.joems.2012.09.005
- Khader, M.M. (2014) On the Numerical Solution and Convergence Study for System of Non-Linear Fractional Diffusion Equations. Canadian Journal of Physics, 92, 1658-1666. http://dx.doi.org/10.1139/cjp-2013-0464
- Khader, M.M., Sweilam, N.H. and Mahdy, A.M.S. (2013) Numerical Study for the Fractional Differential Equations Generated by Optimization Problem Using Chebyshev Collocation Method and FDM. Applied Mathematics and Information Science, 7, 2011-2018. http://dx.doi.org/10.12785/amis/070541
- Khader, M.M., El Danaf, T.S. and Hendy, A.S. (2013) A Computational Matrix Method for Solving Systems of High Order Fractional Differential Equations. Applied Mathematical Modelling, 37, 4035-4050. http://dx.doi.org/10.1016/j.apm.2012.08.009
- Sweilam, N.H. and Khader, M.M. (2010) A Chebyshev Pseudo-Spectral Method for Solving Fractional Order Integro- Differential Equations. ANZIAM Journal, 51, 464-475. http://dx.doi.org/10.1017/S1446181110000830
- Sweilam, N.H., Khader, M.M. and Mahdy, A.M.S. (2012) Numerical Studies for Fractional-Order Logistic Differential Equation with Two Different Delays. Journal of Applied Mathematics, 2012, Article ID: 764894.
- Podlubny, I. (1999) Fractional Differential Equations. Academic Press, New York.
- Miller, K.S. and Ross, B. (1993) An Introduction to the Fractional Calculus and Fractional Differential Equations. John Wily and Sons Inc., New York.
















 , T.M., Konjik, S., Pilipovi
, T.M., Konjik, S., Pilipovi , T.M., Konjik, S., Pilipovi
, T.M., Konjik, S., Pilipovi , S. and Simi
, S. and Simi , S. and Simi
, S. and Simi , S. (2009) Variational Problems with Fractional Derivatives: Invariance Conditions and Nöther’s Theorem. Nonlinear Analysis: Theory, Methods & Applications, 71, 1504-1517. >http://html.scirp.org/file/10-7402723x140.png" class="200" />, S. (2009) Variational Problems with Fractional Derivatives: Invariance Conditions and Nöther’s Theorem. Nonlinear Analysis: Theory, Methods & Applications, 71, 1504-1517.
, S. (2009) Variational Problems with Fractional Derivatives: Invariance Conditions and Nöther’s Theorem. Nonlinear Analysis: Theory, Methods & Applications, 71, 1504-1517. >http://html.scirp.org/file/10-7402723x140.png" class="200" />, S. (2009) Variational Problems with Fractional Derivatives: Invariance Conditions and Nöther’s Theorem. Nonlinear Analysis: Theory, Methods & Applications, 71, 1504-1517.