Applied Mathematics
Vol.05 No.19(2014), Article ID:51234,6 pages
10.4236/am.2014.519286
The Power of Change-Point Test for Two-Phase Regression
To Van Ban, Nguyen Thi Quyen
Department of Mathematics, Haiphong University, Haiphong, Vietnam
Email: quyentthp@yahoo.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 3 September 2014; revised 28 September 2014; accepted 12 October 2014
ABSTRACT
In this paper, the roughness of the model function to the basis functions and its properties have been considered. We also consider some conditions to take the limit of the roughness when the observations are i.i.d. An explicit formula to calculate the power of change-point test for the two phases regression through the roughness was obtained.
Keywords:
Change-Point Test, The Power, The Roughness, Random Design

1. Introduction
Many authors have used the likelihood ratio to study the change-point problem (see [1] [2] ). Worsley, K.J. [3] gave exact approximate bounds for the null distributions of likelihood ratio statistics in two case of known and unknown variance. Simulation study results indicated that the approximation of his upper bound is very good for the small sample size, but the study does not support the case of large one. Koul and H.L, Qian. L. [4] studied the change-point by the maximum likelihood and random design. In the case of known variance, Jaruskova, D. [5] derived an asymptotic distribution of log-likelihood type ratio to detect a change-point from a known (or unknown) constant state to a trend state. Aue A., Horvath, L., Huskova, M. and Kokoszka, P. [1] studied the limit distribution of the trimmed version of the likelihood ratio, from which they received the test statistic to detect a change-point for the polynomial regressions. Researchers have used to take simulation studies on the various scenarios of the parameters of alternative hypothesis to find the power of a test. They have found that it depends on the sample size, variance of error and the behavior of the model function under alternative. For two phases’ regression, Lehmann, E.L. and Romano, J.P. [6] gave a formula to calculate the power of change-point through the noncentral F-distribution.
In this paper, the behavior of the model function under alternative is quantified by the roughness that is used to calculate the power of tests. The present paper is organized in the following way. In Section 2, we give a definition of the roughness of the model function and show some its properties; it is possible to take the limit of the roughness when the sequence of designs converges weakly to a limit design as well as designs are random. In Section 3, we present an explicit formula to calculate the noncentrality parameter of F-test in [6] through the roughness, and then the power of change-point test and some of its limits are considered.
2. The Roughness of the Model Function
To approximate the function 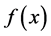 by a given system of functions
by a given system of functions 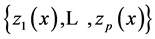 at the given points
at the given points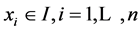 , we consider the model
, we consider the model
 (1)
(1)
 . (2)
. (2)
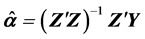 (3)
(3)
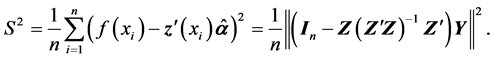 (4)
(4)
We call this value the roughness of the function 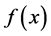 to the system of functions
to the system of functions 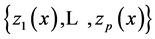 based on the design
based on the design 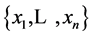 and denote it by
and denote it by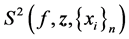 . In the case of a linear trend where
. In the case of a linear trend where 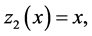
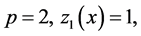
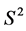 shows the nonlinearity of the curve
shows the nonlinearity of the curve 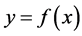 based on observations at
based on observations at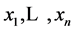 .
.
To study limits cases as well as other purposes, we call a distribution function 






To continue, we will establish some assumptions:
(A2) Trend functions 
Now suppose that (A1) and (A2) hold, we approximate the function 


The estimate for the parameter vector 


where

We also call this value the roughness of the function 



According to [2] , to evaluate the roughness of the model function based on polynomial trend functions

interval 
The following theorem in [7] shows the conditions for occurring the convergence of the estimated parameters and the roughness.
1)
2)
Now, we consider the model (1) where the observations 





where
Theorem 2. Suppose that (A1) and (A2) hold for 
1) 


2)
3) The roughness 
Then
Let 


Because 
Then, according to the assumption 2),
which follows that elements of the matrix 
Similar arguments yield
Consequently, we obtain the limit

Note that 
where
Because 

Inasmuch as 
Again, according to the central limit theorem and (9),
Combining the above with the fact that 
This completes the proof of the theorem.
3. Applications to the Change-Point Test
Suppose that the model function is defined as:

where 







where 


Let
Using matrix notations, the Equation (12) is written as

We are interested in testing the hypothesis of structural stability against the alternative of a regime switch at a sometime 

Let 










The least-squares estimate of 











We already know that (see Lehmann, E.L. and Romano, J.P. [6] ): Under 

will be distributed 


where 



and 

are orthogonal projections of 






We note that 

Now, we call 



Theorem 3. If assumptions (A2), (A3) hold then the power of test (16) is defined by

Remark. Theorem 3 shows an explicit formula of the power of change-point test. In the case of 






To increase signal-to-noise ratio, we can decrease the noise or increase the roughness of the model function. When the variance 
With the sample size 







Corollary 1. If the assumptions in Theorem 3 are satisfied then the following limits hold:
1)
2)
Limits of the powers are obtained by the following corollary.
Corollary 2. 1) With the same conditions as in Theorem 3, assume that 


2) Furthermore, if the model function 


Proof. First of all, it is easy to see that
where

Because 
Moreover, 

Now, according to Theorem 1,
then 2) is implied straight from 1).
References
- Aue, A., Horvath, L., Huskova, M. and Kokoszka, P. (2008) Testing for Changes in Polynomial Regression. Bernoulli, 14, 637-660. http://dx.doi.org/10.3150/08-BEJ122
- Berkes, I., Horvath, L. and Schauer, J. (2011) Asymptotics of Trimmed CUSUM Statistics. Bernoulli, 17, 1344-1367. http://dx.doi.org/10.3150/10-BEJ318
- Worsley, K.J. (1983) Testing for a Two-Phase Multiple Regression. Technometrics, 25, 35-42. http://dx.doi.org/10.1080/00401706.1983.10487817
- Koul, H.L. and Qian, L. (2002) Asymptotics of Maximum Likelihood Estimator in a Two-Phase Linear Regression Model. Journal of Statistical Planning and Inference, 108, 99-119. http://dx.doi.org/10.1016/S0378-3758(02)00273-2
- Jaruskova, D. (1998) Testing Appearance of Linear Trend. Journal of Statistical Planning and Inference, 70, 263-276. http://dx.doi.org/10.1016/S0378-3758(97)00184-5
- Lehmann, E.L. and Romano, J.P. (2005) Testing Statistical Hypotheses. 3th Edition, Springer, New York, USA, 277- 282.
- Ban, T.V., Quyen, N.T. and Ha, P.T. (2013) The Roughness of the Model Function to the Basis Functions. Journal of Mathematics and System Science, 3, 385-390.
- Bischoff, W. and Miller, F. (2000) Asymptotically Optimal Test and Optimal Designs for Testing the Mean in Regression Models with Applications to Change-Point Problems. Annals of the Institute of Statistical Mathematics, 52, 658- 679. http://dx.doi.org/10.1023/A:1017521225616






































