Applied Mathematics
Vol.05 No.21(2014), Article ID:52123,8 pages
10.4236/am.2014.521316
Finding Gaussian Curvature of Lifespan Distribution
William W. S. Chen
Department of Statistics, The George Washington University, Washington DC, USA
Email: Williamwschen@gmail.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 24 September 2014; revised 20 October 2014; accepted 2 November 2014
ABSTRACT
The objective of this paper is to review the lifespan model. This paper will also suggest four additional general alternative computational methods not mentioned in Kass, R.E. and Vos, P.W. [1] [2] . It is not intended to compare the four formulas to be used in computing the Gaussian curvature. Four different formulas adopted from Struik, D.J. [3] are used and labeled here as (A), (B), (C), and (D). It has been found that all four of these formulas can compute the Gaussian curvature effectively and successfully. To avoid repetition, we only presented results from formulas (B) and (D). One can more easily check other results from formulas (A) and (C).
Keywords:
Christoffel Symbols, Gamma, Gaussian Curvature, Inverse Gaussian, Metric Tensor, Mixed Riemann Curvature Tensor, Weibull

1. Introduction
The exponential, Weibull, gamma, lognormal, inverse Gaussian, and generalized gamma distributions are the most frequently used parametric lifespan models. Among the most commonly used lifespan models, the author has chosen three that he has studied since he was a graduate student. Lawless, J.F. [4] has suggested at least six different categories in applications. In the early 1980s, Chen, W. [5] -[8] pursued this area of study for two basic reasons. First, there was industrial interest. Engineering, medicine and biological sciences used the lifespan model to predict the best future values of their censored samples. Secondly, the author wanted to expand on his dissertation. If we summarized the last forty years of statistical research, the scientific community has had two fundamental topics to study. The first fundamental topic: suppose we are given a set of lifetime data, how do we decide which lifespan model best describes the data? A second interesting topic for researchers is data sets that can be “censored data”, where experiments in the sample only provide a lower or upper bound of lifetime. For example, Gupta, A. [9] presented results of a life-test on ten laboratory mice following inoculation with a uniform culture of human tuberculosis. The test was terminated with the death of the seventh specimen. Thus, the sample in this case was Type-II single right censored. Gupta then assumed that log lifespan was distributed normally with mean 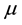 and variance
and variance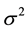 , and then carried out the analysis as described in reference [10] . Chen, W. and Balakrishnan, N. [10] [11] have computed over one hundred thousand numerical integrations to find the moments of inverse Gaussian model and lognormal model, and then standardized these moments to find the best linear unbiased predicted sequences (EBLUP). Using these computed sequences it will give us the best prediction of the missing observations. However, in this paper we switch our attention to the geometrical property of lifespan model. To make it easier to follow what we have accomplished in this paper, we summarized our approach into four systematic steps to compute the Gaussian curvature: Step 1―compute the coefficients of the expected Fisher Information Matrix or coefficients of the first fundamental form, namely, E, F and G; Step 2―compute the needed first or second derivative of E, F and G, and thus the six Christoffel symbols; Step 3―apply formula (B) or (D), which necessitates in the computation of the mixed Riemann curvature tensors
, and then carried out the analysis as described in reference [10] . Chen, W. and Balakrishnan, N. [10] [11] have computed over one hundred thousand numerical integrations to find the moments of inverse Gaussian model and lognormal model, and then standardized these moments to find the best linear unbiased predicted sequences (EBLUP). Using these computed sequences it will give us the best prediction of the missing observations. However, in this paper we switch our attention to the geometrical property of lifespan model. To make it easier to follow what we have accomplished in this paper, we summarized our approach into four systematic steps to compute the Gaussian curvature: Step 1―compute the coefficients of the expected Fisher Information Matrix or coefficients of the first fundamental form, namely, E, F and G; Step 2―compute the needed first or second derivative of E, F and G, and thus the six Christoffel symbols; Step 3―apply formula (B) or (D), which necessitates in the computation of the mixed Riemann curvature tensors 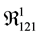 and
and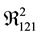 , then subsequent computation of the inner product of this tensor with the metric tensor, F or G, results in the covariant Riemann curvature tensor
, then subsequent computation of the inner product of this tensor with the metric tensor, F or G, results in the covariant Riemann curvature tensor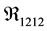 , and Step 4―observe that the Gaussian curvature has a very simple relation to Riemann symbols of the second kind. By adhering to this procedure, the correct Gaussian curvature will be calculated. In the case where
, and Step 4―observe that the Gaussian curvature has a very simple relation to Riemann symbols of the second kind. By adhering to this procedure, the correct Gaussian curvature will be calculated. In the case where 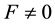 or the parametric lines on the surface are not orthogonal, the computational procedure can be extremely tedious such as our model 2. It is always prudent to find a proper transformation to form an orthogonal system of parametric lines in order to simplify the computational procedures.
or the parametric lines on the surface are not orthogonal, the computational procedure can be extremely tedious such as our model 2. It is always prudent to find a proper transformation to form an orthogonal system of parametric lines in order to simplify the computational procedures.
2. Formulas
In this section, we suggest four formulas that can be used to compute the Gaussian curvature.
(A) 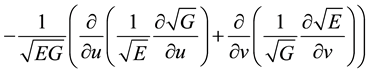
(B) 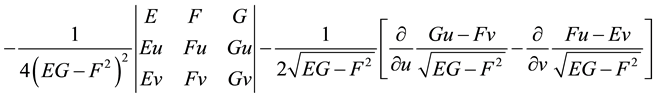
(C)  where
where 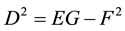
(D) 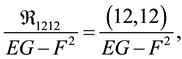 where
where 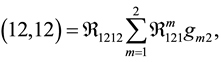

sum on m, where the quantities of  are components of a tensor of the fourth order. This tensor is called the mixed Riemann curvature tensor. Notice that g11, g12 and g22 are simply tensor notation for E, F and G. Formula (B) was developed by G. Frobenius while formula (C) was derived by J. Liouville. Clearly, formula (A) is a special case that is valid only when the parametric lines are orthogonal. Formula (D) is a general form represented in Riemann symbols of the first and second kind, respectively. In formula (D),
are components of a tensor of the fourth order. This tensor is called the mixed Riemann curvature tensor. Notice that g11, g12 and g22 are simply tensor notation for E, F and G. Formula (B) was developed by G. Frobenius while formula (C) was derived by J. Liouville. Clearly, formula (A) is a special case that is valid only when the parametric lines are orthogonal. Formula (D) is a general form represented in Riemann symbols of the first and second kind, respectively. In formula (D), 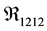 , the inner product of the mixed Riemann curvature tensor and the metric tensor, is called the covariant Riemann curvature tensor; it is a covariant tensor of the fourth order. The components
, the inner product of the mixed Riemann curvature tensor and the metric tensor, is called the covariant Riemann curvature tensor; it is a covariant tensor of the fourth order. The components  and
and 

We can immediately calculate the same results as found from formula (A) while formula (D) results in a Riemann representation. In this way, we have supplied some more general alternative methods to compute the Gaussian curvature, including the case when
3. Curvature of Three Life Span Model
In this section, we give the needed result of derivation by applying formula (B) and (D) for computing our Gaussian curvature. The process and formulas (B) and (D) are complicated, so we decided to tabulate formulas by units, which yields some advantages. It turns out that it is much easier to check partial results than to check the whole equation. It is also much easier to understand why and how we obtain the final results, or in the event of an error it should be much easier to correct it. In model 1, we will deal with Gamma Families. In model 2, we discuss the Weibull Families. In model 3, density function is of form of Inverse Gaussian families.
Model 1: A random variable X has a gamma distribution if its probability density function is of form
Now, the information unit needed to apply the formula (B) has been available. In Table 1, we tabulate the most important coefficient of the first fundamental form and their derivatives. It should be aware that F, Fu and Fv are equal zero. Using one of the fundamental properties of determinants we know that three by three’s determinant is zero. This will greatly improve the efficiency of our computation process.
In Table 2, we tabulate what is needed of partial results in formula (B). Also due to the fact that

Notice that the detailed results of six Christoffel symbols are given in summary Table 3. Finally, we list that the formula (D) required results of symbol of Riemann and Gaussian curvature in Table 4. Be awe that
Table 1. List computing results of coefficient of the first fundamental form and their derivatives.
Table 2. List important partial results of computing formula.
Where
Table 3. List the computed results of the six Christoffel symbols.
Table 4. List the computed results of symbol of Riemann and Gaussian curvature.

Model 2: A random variable X has a Weibull Distribution if its probability density function is of form
We are ready to apply the formula (B). The first term involves the 3 × 3 determinant expansion. From the previous computation we aware that two terms of expansion are zero, i.e.

This means the first term of the determinant can be ignored. Also due to the fact that


Using the formula (D) to find the Weibull Distribution Gaussian curvature is our next mission. This is a somewhat messy one, as no short cut can be utilized, since two of the components of Riemann symbols have nonzero values. We show the computation as follows.

Model 3: A random variable X has an Inverse Gaussian Distribution if its probability density function is of form
Again, the information unit needed to apply the formula (B) has been available. Again, we aware that F, Fu and Fv are all equal zero. Hence the first term of determinant is zero. Also due to the fact that 

Notice that the detailed results of six Christoffel symbols are given in summary table. Next, we apply the formula (D) to compute the curvature as below.

To summarize and compare the Gaussian curvature computed in Equations (3.1), (3.2), (3.3), (3.4), (3.5), and (3.6), it is obvious that formula (B) and (D) give us the identical results.
4. Concluding Remark
It is also a well-known fact that two surfaces which have the same Gaussian curvature are always isometric and bending invariant. For instance, Struik, D.J. on p. 120 provided an excellent example that demonstrated a correspondence between the points of a catenoid and that of a right helicoid, such that at corresponding points, the coefficients of the first fundamental form and the Gaussian curvatures are dentical. In fact, one surface can pass into the other by a continuous bending. This has been demonstrated by the deformation of six different stages. However, if the Gaussian curvature is different, the two surfaces will not be isometric. For example, a sphere and plane are not locally isometric because the Gaussian curvature of a sphere is nonzero while the Gaussian curvature of a plane is zero. This is why any map of a portion of the earth must distort distances. One of the most important theorems of the 19th century is “Theorema Egregium”. Many mathematicians at the end of the 18th century, including Euler and Monge, had used the Gaussian curvature, but only when defined as the product of the principal curvatures. Since each principal curvature of a surface depends on the particular way where the surface is defined in R3, there is no obvious reason for the product of the principal curvatures to be intrinsic to that particular surface. Gauss published in 1827 that the product of the principal curvatures depends only on the intrinsic geometry of the surface revolutionized differential geometry. Gauss wrote “‘The Gaussian curvature of a surface is a bending invariant’, ‘a most excellent theorem’, ‘This is a Theorema egregium’”. In this theorem, Gauss proved that the Gaussian curvature, K, of a surface, depends only on the coefficient of the first fundamental form and their first and second derivatives. This important geometric fact will link the concepts of bending and isometric mapping.
References
- Kass, R.E. and Vos, P.W. (1997) Geometrical Foundations of Asymptotic Inference. John Wiley & Sons, Inc., New York. http://dx.doi.org/10.1002/9781118165980
- Kass, R.E. (1989) The Geometry of Asymptotic Inference (with Discussion). Statistical Science, 4, 188-234.
- Struik, D.J. (1961) Lectures on Classical Differential Geometry. 2nd Edition, Dover Publications, Inc., New York.
- Lawless, J.F. (1982) Statistical Models and Methods for Lifetime Data. John Wiley & Sons, Hoboken.
- Chen, W.W.S. (1980) On the Tests of Separate Families of Hypotheses with Small Sample Size. Journal of Statistical Computation and Simulation, 2, 183-187. http://dx.doi.org/10.1080/00949658008810406
- Chen, W.W.S. (1982) Simulation on Probability Points for Testing of Lognormal or Weibull Distribution with a Small Sample. Journal of Statistical Computation and Simulation, 15, 201-210. http://dx.doi.org/10.1080/00949658208810583
- Chen, W.W.S. (1987) Testing Gamma and Weibull Distribution: A Comparative Study. Estadistica, 39, 1-26.
- Chen, W.W.S. (1983) Testing Lognormal and Exponential Distributions: Estimation of Percentile Points. American Journal of Mathematical and Management Sciences, 3, 165-196. http://dx.doi.org/10.1080/01966324.1983.10737123
- Gupta, A.K. (1952) Estimation of the Mean and Standard Deviation of a Normal Population from a Censored Sample. Biometrika, 39, 260-273. http://dx.doi.org/10.1093/biomet/39.3-4.260
- Balakrishnan, N. and Chen, W.W.S. (1999) Handbook of Tables for Order Statistics from Lognormal Distributions with Applications. Kluwer Academic Publishers, Norwell. http://dx.doi.org/10.1007/978-1-4615-5309-0
- Balakrishnan, N. and Chen, W.W.S. (1997) CRC Handbook of Tables for Order Statistics from Inverse Gaussian Distributions with Applications. CRC Press, Boca Raton.
- Gray, A. (1993) Modern Differential Geometry of Curves and Surfaces. CRC Press, Inc., Boca Raton.
Appendix
Next, we define the six well known Christoffel symbols see Struik, D.J. or Gray A. [12]
we applied the following integral results
we define the nth derivative of the gamma function:
















