Received 14 January 2015; accepted 2 February 2015; published 5 February 2015

ABSTRACT

In this paper we study estimator of mean residual life function in fixed design regression model when life times are subjected to informative random censoring from both sides. We prove an asymptotic normality of estimators.

Keywords:

Informative Censoring, Power Estimator, Regression, Mean Residual Lifetime

1. Introduction

In survival data analysis, response random variable (r.v.) Z, the survival time of a individual (in medical study) or failure time of a machine (in industrial study) that usually can be influenced by r.v. X, is often called prognostic factor (or covariate). X represents e.g. the dose of a drug for individual or some environmental conditions of a machine (temperature, pressure,…). Moreover, in such practical situations it often occurs that not all of survival times 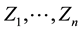of n identical objects are complete observed, that they can be censored by other r.v.-s.

In this article we consider a regression model in which the response r.v.-s are subjected to random censoring from both sides.

We first introduce some notations. Let the support of covariate is the interval [0,1] and we describe our regression results in the situation of fixed design points at which we consider nonnegative independent responses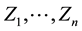. Suppose that these responses are censored from the left and right by nonnegative r.v.-s 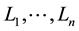and 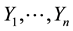and the observed r.v.-s at design points x_i are in fact

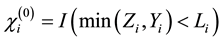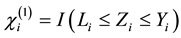with, , and

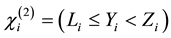, where denote the indicator of event A. Hence the observed data is consist of n vectors:

.

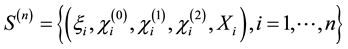Assume that components of vectors 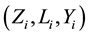are independent for a given covariate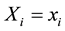. In sample 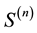the r.v.-s of interest Z_i’s are observable only when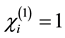. Denote by F_x, K_x and G_x the conditional distribution functions (d.f.-s) of r.v.-s Z_x, L_x and Y_x respectively, given that and suppose that they are continuous.

Let H_x and N_x are conditional d.f.-s of and for. Then it’s easy to see that with,. In particular, if for all, , then we obtain the interval random censoring model.

The main problem in considered fixed design regression model is consist on estimation the conditional d.f. F_x of lifetimes and its functionals from the samples under nuisance d.f.-s K_x and G_x. The first product-limit type estimators for F_x in the case of no censoring from the left (that is or) proposed by Beran [1] and has been investigated by many authors (see, for example [2] [3] ). In this article supposing that the random censoring from both sides is informative we use twice power type estimator of F_x from [4] [5] for estimation the mean conditional residual life function. Suppose that d.f.-s K_x and G_x are expressed from F_x by following parametric relationships for all:

(1.1)

where and are positive unknown nuisance parameters, depending on the covariate value x. Informative model (1.1) include the well-known conditional proportional hazards model (PHM) of Koziol-Green, which follows under absence of left random censorship (that is). Estimation of F_x in conditional PHM is considered in [6] . Model (1.1) one can considered as an extended two sided conditional PHM. In the case of no covariates, model (1.1) first is proposed in [7] [8] .

It is not difficult to verify that from (1.1) one can obtain following expression of d.f. F_x:

(1.2)

where, and, , 1, 2, with

. Then estimator of F_x one can constructed by natural plugging method as follows:

(1.3)

Here, ,

and

,

are smoothed estimators of and, used Gasser-Müllers weights:

,

, is a known probability density function (kernel), and is a sequence of positive constants tending to 0 as, called the bandwidth sequence. Note that in the case of no censoring from the left the estimator (1.3) is coincides with estimator in conditional Koziol-Green model in [6] . Note also that a class of power type estimators for conditional d.f.-s for several models authors have considered in book [9] . Estimator (1.3) was presented in [4] and its asymptotic properties have been investigated in [5] . Now we demonstrate some of these results.

2. Asymptotic Results for Estimator of Conditional Distribution Function

For asymptotic properties of estimator (1.3) we need some notations. For the design points and kernel π we denote

,

.

Let and are lower and upper bounds of support of d.f. F_x. Then by (1.1):

.

In [4] authors have proved the following property of two sided conditional PHM (1.1).

Theorem 2.1 [5] . For a given covariate x, the model (1.1) holds if and only if r.v. and the vector are independent.

This characterization of submodel (1.1) plays an important role for investigation the properties of estimator (1.3).

Let’s introduce some conditions:

(C1) As, , ,.

(C2) π is a probability density function with compact support for some, with and, where is some constant.

(C3) and exist and are continuous for and, with.

(C4) and exist and are continuous for.

Let’s also denote:,

Note that existence of all these derivatives follows from conditions (C3) and (C4). Now we state some asymptotic results for estimator (1.3), which have proved in [5] .

Theorem 2.2 [5] (uniform strong consistency with rate). Assume (C1)-(C4),. If,

, as, then

Theorem 2.3 [5] (almost sure asymptotic representation with weighted sums). Under the conditions of Theorem 2.2 with, we have for:

where

and as,

Corollary. Under the conditions of Theorem 2.3, and as, for:

.

Theorem 2.4 [5] (asymptotic normality). Assume (C1)-(C4)..

(A) If and, then for, as,

(B) If for some, then for, as,

where

,

with

It is necessary to note that Theorems 2.1-2.4 are extended the corresponding theorems in conditional PHM of Koziol-Green from [6] .

In the next Section 3 we use these theorems for investigation the properties of the estimator of mean conditional residual life function.

3. Asymptotic Normality of Estimator of Mean Conditional Residual Life Function

The conditional residual lifetime distribution defined as

,

i.e. the d.f. of residual lifetime, conditional on survival upon a given time t and at a given value of the covariate x. Then for,

. (3.1)

One of main characteristics of d.f. (3.1) is its mean, i.e. mean conditional residual life function

. (3.2)

We estimate functional by plugging in estimator (1.3) instead of F_x in (3.2). But from section 2 we know that estimator (1.3) have consistent properties in some interval with. Therefore, we will consider the following truncated version of (3.2):

. (3.3)

Now we estimate (3.3) by statistics

. (3.4)

We have following asymptotic normality result.

Theorem 3.1. Assume (C1)-(C3) in with,.

(A) If and, as, then

(B) If for some, then as,

Here

,

,

and from Theorem 2.4.

Proof of theorem 3.1. By standard manipulations and Theorem 2.3 we have that

,

where

For and we use Theorem 2.3, for and, Theorem 2.2. Then we see that all these re-

mainder terms uniformly on almost surely have order.

Now statements (A) and (B) of theorem follows from corresponding statements of the theorem 2.4 by standard arguments.

Theorem 3.1 is proved.

Acknowledgements

This work is supported by Grant F4-01 of Fundamental Research Found of Uzbekistan.

References