Applied Mathematics
Vol.05 No.16(2014), Article ID:49431,12 pages
10.4236/am.2014.516242
Multiple Endemic Solutions in an Epidemic Hepatitis B Model without Vertical Transmission*
Nelson Owuor Onyango
School of Mathematics, CBPS, University of Nairobi, Nairobi, Kenya
Email: nelsonowuor@gmail.com, onyango@uonbi.ac.ke
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 12 July 2014; revised 13 August 2014; accepted 23 August 2014
ABSTRACT
This paper examines the dynamics of Hepatitis B via a Susceptible Exposed Infectious Recovered (SEIR) type epidemic model. Previous studies have shown that Hepatitis B is characterized by multiple endemic solutions, a matter which may be of concern in developing control strategies. We identify the possible causes of multiple endemic solutions in a Hepatitis B model and conclude that the dependance of the probability of carriage development
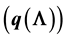 on the force of infection
on the force of infection
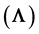 is the main reason for multiple endemicity. Other factors such as a large proportion of infants that are not vaccinated
is the main reason for multiple endemicity. Other factors such as a large proportion of infants that are not vaccinated
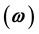 may also enhance the possibility of multiple endemicity. The role of carriers may also play a key role in the possibility of such complex dynamics, i.e., when infectiousness of carriers-
may also enhance the possibility of multiple endemicity. The role of carriers may also play a key role in the possibility of such complex dynamics, i.e., when infectiousness of carriers- is high, the probability of existence of multiple endemic equilibrium solutions is increased. In our arguments, the traditional reproduction number
is high, the probability of existence of multiple endemic equilibrium solutions is increased. In our arguments, the traditional reproduction number
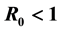 which we define here by a function
which we define here by a function
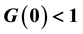 does not imply stability of disease-free equilibrium.
does not imply stability of disease-free equilibrium.
Keywords:
SEIR Epidemic Models, Endemic Equilibriums, Hepatitis B

1. Introduction
Multiple endemicity (often arising from a backward bifurcation) refers to a situation where a dynamic system (ODE or PDE) converges in its asymptotic dynamics to two different equilibrium states, under the same set of parameter values. The theory of attractors and mutation of such attractors with change in parameter values is studied extensively under the field of Bifurcation Theory [1] [2] .
The dynamics of Hepatitis B (HepB) virus can be classified into three major world prevalence regions [3] :
・ Sub-Sahara Africa where horizontal infection among lower age groups is the dominant form of transmission, together with perinatal transmission (mother to child transmission within the first year of the infant). The region is hyper-endemic (over 10% carrier prevalence) since more infection among children leads to higher carrier prevalence.
・ South East Asia where vertical transmission is reportedly more significant. Then other forms of childhood infection also contribute. This region is hyper-endemic as well.
・ Europe and North America where only transmission among adults contributes to infection. Sexual contact and intra-venous drug use are the key contact pathways. The region is low-endemic as very few adults deve- lop to carrier state after acute infection.
We model a scenario that captures the Sub-Saharan prevalence zone: where vertical transmission could play a role in transmission; immunization largely done at child birth without screening and mainly heterosexual be- havior is assumed in the population. Although HepB can be effectively vaccinated against, there are public- health concerns we wish to address that may affect the optimal vaccination against the disease and global control strategies. Recent developments in the dynamics of HepB virus indicate existence of complex dynamics such as multiple endemicity, heterogenous prevalence among population groups, among others, which may be of great concern to vaccination efforts.
This paper aims to investigate the following scenarios in the context of a developing country (Sub-Sahara Africa scenario):
・ Causes for existence of multiple endemic scenario in an age-structured model. This phenomenon has been observed in a model without age structure [4] . Multiple endemicity may offer a great challenge to vaccina- tion campaign, since even in cases when vaccination is effective, the possibility of coexistence of higher and lower disease endemic states may complicate a vaccination effort aimed at disease control.
・ The threshold conditions for HepB endemicity. The reproduction number G0 < 1 does not imply the stability of disease-free equilibrium in this case.
The paper is organized into the following sections: Section 1 offers an introduction and justification for modeling HepB. In Section 2, we describe the model structure and the equations for the population dynamics. In Section 3, we consider the model of proportions which is also referred to as the projected model due to the fact that it captures equilibrium dynamics in terms of the vital (birth and death) parameters. In Section 4, we derive a fixed-point equation using the equation for the force of infection and characterize the equilibrium solutions via this fixed-point equation. Section 5, the multiple endemicity conditions are obtained for this case of a HepB model without vertical transmission.
2. Model Structure
We develop an age-structured compartmental model with the following compartments: S(a,t) are susceptible individuals; L(a,t) are latently infected individuals who are infected but not yet infectious; I(a,t) are acute infected individuals who are quite infectious. But they move on quickly to the next state, the chronic carriage state, so they do not contribute strongly to new infections; C(a,t) are carriers who in some literature (see e.g. [5] ) are referred to as chronic infectious individuals. They stay in this state for a long time and contribute more to new infections than the acute infectious group; and R(a,t) are the immune or else referred to as recovered in- dividuals.
A better view of the model structure is displayed using the Figure 1 and Figure 2.
The following parameters define movement between the compartments:
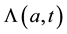 is the force of infection which varies with age and time;
is the force of infection which varies with age and time;
 defines the rate of movement from latent state to infectious state;
defines the rate of movement from latent state to infectious state;
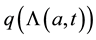 is the probability that an individual who is infectious becomes a carrier, so
is the probability that an individual who is infectious becomes a carrier, so
 is the probability that such a person becomes immune;
is the probability that such a person becomes immune;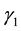 ,
,
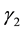 are recovery rates from infectious and carrier states, respectively;
are recovery rates from infectious and carrier states, respectively;
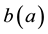 is the age-dependent birth rate, only used in the boundary conditions into
is the age-dependent birth rate, only used in the boundary conditions into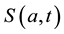 ,
,
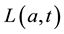 and
and
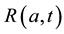 states;
states;

Define the total population for an age group by
Figure 1. The figure show proportions of new births into population compartments, where







Figure 2. Flow chart of HepB virus transmission.

and


while

Therefore

Given




We therefore have the following increments into


New births into the susceptible class are given by
into the latent class by
and into the immune class by
We use the notation
Under the assumptions above, we describe the full model for the spread of HepB by the system of PDEs below,

which we denote in matrix form by



where

and
The total population has an exponential decay and is obtained by summing the variables in (1.4)



System (2) is known as the stable population model and has a unique persistent age distribution profile (see e.g., [6] - [8] )
3. Projected Model
The projected model represents the situation when the population dynamics are at their equilibrium. This state can be achieved by transforming the state variables into proportions, i.e., modify system (1.4) into a model of proportions. This transformation eliminates the vital dynamics (birth and death) from the model and hence the reason why we refer to the resultant model as the projected model.
Consider the proportions of the population in each compartment in the model at age

and
where

lation is thus obtained next. Applying the quotient rule on the derivative
Define

Then the boundary condition for the susceptible class reads:
Proceeding the same way for all the state variables, we obtain the projected system (1.8), which is in- dependent of population dynamics, except for birth rate that appears in the model within the boundary con- ditions. The projected system now reads:

which can be expressed in matrix form as



where

4. Force of Infection
The force of infection

In this case, we have an additional infection from carriers, where the parameter

of carriers relative to acute infected group and




We similarly obtain the force of infection for the projected model at equilibrium:

In the ensuing discussions, we analyse a reduced model, i.e., the model without vertical transmission. Vertical transmission characterizes a situation where a fraction of newborns are born with the disease, having been infected before or at birth. In this setting, the parameter


vertical transmission. Recall that


The model without vertical transmission is thus,



For this subcase


We obtain expressions for i(b) and c(b) and insert in Equation (1.11).
Consider system (1.12) at its equilibrium such that,

Define


and

where
Inserting these expressions in Equation (1.11), we obtain

By the definition of the force of infection, one observes that


Definition 1. The Basic Reproduction Number is defined as the spectral radius of the operator

the m-th generation of new infective individuals coming from an initial density of infective individuals.
The Basic Reproduction number


Theorem 1. Assume that the force of infection


where
Proof. We make the following transformations on Equation (1.13):




We seek solutions





The solutions



and

Hence

The endemic solutions (non-trivial solutions) satisfy

and we define the Basic Reproduction Number of the system (1.4) by [9]

Remark 1. The equation
is thus the main determinant for dynamics of the system (1.12). Solutions to system (1.12) correspond to solu- tions to the fixed-point equation.



Remark 2. Proposition (1) has been applied in studies of equilibrium dynamics, stability and bifurcation in epidemic models (see e.g. [6] [9] [13] . In particular, it has been applied to study the question of backward bifurcation in [16] - [18] .
5. Multiple Endemicity
We seek to establish conditions under which exactly two endemic solutions may occur.
Lemma 1.
Proof.
Since










Theorem 2. Assume





(i)
(ii) there exists
(iii)
Corollary 1. If conditions in Theorem (2) hold, then the Equation (1.12) has exactly two endemic solutions if
(i)
(ii) there exists one
Proof. Since
then

If there exists


Making


Remark 3. We make the following two useful remarks:
1.







2. One also observes the following relationships between

(i)
(ii)
To make this observation, we re-write Equation (1.22) in the two forms below:


where








3. The model with vertical transmission shall be considered in further work. The model is illustrated below. Consider Equation (1.8) at its equilibrium, i.e., no time dependance. We also assume that vertical transmission occurs at birth, i.e.,



6. Conclusions
Multiple endemicity, arising from a backward bifurcation is a phenomenon that has been studied in a number of epidemic models [19] [20] . Studies have also shown similar dynamics with HepB for some set of realistic parameter values [4] . Multiple endemicity has been observed mainly in models of HepB especially when the carrier prevalence is high. Besides, HepB has also been shown to be characterized by heterogenous dynamics such as heterogenous prevalence (1% to 90%) [4] . Such complex dynamics may affect the ability to design a global control strategy to deal with HepB. Generally speaking, HepB is one of the most significant STIs especially in the South East Asia and Africa. Global figures show that viral Hepatitis is 10 times more common than HIV infection despite the fact that a global viral hepatitis treatment program is still a long way from becoming a reality [21] . Vaccination and antiviral treatments are available but rare especially in developing countries.
We studied the solutions of an SEIR HepB model and their stability via the force of infection. This approach has been used to determine equilibrium solutions and their stability in age-structured models, (see e.g., [9] ). We make use of this approach to characterize the conditions for multiple endemic states from a fixed-point equation derived from an equation for the force of infection.
We investigated the role of the following parameters in determining the dynamics of the disease, in line with results of [4] :
・

・

・

・

In further work, we shall incorporate the parameter

Acknowledgements
This work was done at the Institute of Biometry and Biomathematics, Helmholtz Centre-Munich, Germany, under the German DAAD support grant. The work was partly done during a postdoctoral visit at SLU in Uppsala, courtesy of a grant by the International Science Program (ISP)-Uppsala, Sweden. I wish to thank the University of Nairobi for granting me leave to finish the work.
Funding
Funding was partly from German DAAD postgraduate support grant and Swedish ISP Program (Uppsala University).
Cite this paper
Nelson OwuorOnyango, (2014) Multiple Endemic Solutions in an Epidemic Hepatitis B Model without Vertical Transmission. Applied Mathematics,05,2518-2529. doi: 10.4236/am.2014.516242
References
- 1. Kuznetsov, A.Y. (2004) Elements of Applied Bifurcation Theory. 3rd Edition, Springer, Berlin.
http://dx.doi.org/10.1007/978-1-4757-3978-7 - 2. Guckenheimer, J. and Holmes, P. (1983) Nonlinear Oscillations, Dynamical Systems and Bifurcations of Vector Fields. Springer, Berlin.
http://dx.doi.org/10.1007/978-1-4612-1140-2 - 3. Edmunds, W.J., Medley, G.F. and Nokes, D.J. (1996) The Transmission Dynamics and Control of Hepatitis-B Virus in the Gambia. Statistics in Medicine, 15, 2215-2233.
http://dx.doi.org/10.1002/(SICI)1097-0258(19961030)15:20<2215::AID-SIM369>3.0.CO;2-2 - 4. Medley, G.F., Lindop, N.A., Edmunds, W.J. and Nokes, D.J. (1996) Hepatitis-B Virus Endemicity: Heterogeneity, Catastrophic Dynamics and Control. Nature Medicine, 7, 916-624.
- 5. Zhao, S., Xu, Z. and Lu, Y. (2000) A Mathematical Model of Hepatitis B Virus Transmission and Its Application for Vaccination Strategy in China. International Journal of Epidemiology, 29, 744-752.
http://dx.doi.org/10.1093/ije/29.4.744 - 6. Inaba, H. (2006) Mathematical Analysis of an Age Structured SIR Epidemic Model with Vertical Transmission. Discrete and Continuous Dynamical Systems, Series B, 6, 69-96.
http://dx.doi.org/10.3934/dcdsb.2006.6.69 - 7. Webb, G.F. (1985) Theory of Non-Linear Age Dependent Population Dynamics. Marcel Dekker Inc., New York.
- 8. Pruess, J. and Schappacher, W. (1984) Semigroup Methods for Age-Structured Population Dynamics. In: Chatterji, S., Fuchstainer, B., Kulisch, U. and Liedl, R., Eds., Jarbuch überblicke Mathematik, Viewing Verlag.
- 9. Thieme, H.R. (2003) Mathematics in Population Biology. Princeton University Press, New Jersey.
- 10. Dietz, K. and Schlenze, D. (1985) Mathematical Models for Infectious Disease Statistics, a Celebration of Statistics. In: Atkinson, A.C. and Fienberg, S.E., Eds., The ISI Centenary Volume, Springer-Verlag, New York.
- 11. Müller, J. (1998) Optimal Vaccination Patterns in Age-Structured Populations. SIAM Journal on Applied Mathematics, 59, 222-241.
http://dx.doi.org/10.1137/S0036139995293270 - 12. Grippenberg, G. (1983) On a Non-Linear Intergral Equation Modeling an Epidemic in an Age-Structured Population. Journal for Pure and Applied Mathematics, 341, 56-67.
- 13. Inaba, H. (1990) Threshold and Stability Results for an Age-Structured Epidemic Model. Journal of Mathematical Biology, 28, 411-434.
http://dx.doi.org/10.1007/BF00178326 - 14. Diekmann, O., Heesterbeek, J.A.P. and Metz, J.A.J. (1990) On the Definition and the Computation of the Basic Reproduction Ratio R0 in Models for Infectious Diseases in Heterogeneous Populations. Journal of Mathematical Biology, 28, 365-382.
http://dx.doi.org/10.1007/BF00178324 - 15. Li, J., Blakeley, D. and Smith, R.J. (2011) The Failure of R0. Computational and Mathematical Methods in Medicine, 2011, Article ID: 527610.
- 16. Chavez, C.C. and Song, B. (2004) Dynamical Models of Tuberculosis and Their Applications. Mathematical Bioscience and Engineering, 1, 361-404.
http://dx.doi.org/10.3934/mbe.2004.1.361 - 17. Hadeler, K.P. and Van den Driessche, P. (1997) Backward Bifurcation in Epidemic Control. Mathematical Biosciences, 146, 15-35.
http://dx.doi.org/10.1016/S0025-5564(97)00027-8 - 18. Sharomi, O., Podder, C.N., Gumel, A.B., Elbasha, E.H. and Watmough, J. (2000) Role of Incidence Function in Vaccine-Induced Backward Bifurcation in Some HIV Models. Mathematical Biosciences, 210, 436-463.
http://dx.doi.org/10.1016/j.mbs.2007.05.012 - 19. Garba, S.M., Gumel, A.B. and Bakar, M.R.A. (2008) Backward Bifurcations in Dengue Transmission Dynamics. Mathematical Biosciences, 215, 11-25.
http://dx.doi.org/10.1016/j.mbs.2008.05.002 - 20. Reluga, T.C., Medlock, J. and Perelson, A.S. (2008) Backward Bifurcations and Multiple Equilibria in Epidemic Models with Structured Immunity. Journal of Theoretical Biology, 252, 155-165.
http://dx.doi.org/10.1016/j.jtbi.2008.01.014 - 21. Robotin, M.C. (2011) Hepatitis B Prevention and Control: Lessons from the East and the West. World Journal of Hepatology, 3, 31-37.
http://dx.doi.org/10.4254/wjh.v3.i2.31
NOTES
*Modeling multiple endemicity in Hepatistis B: This research work was motivated by a result of a previous work published by Medley G. in 2001, showing simulated results of multiple endemicity for Hepatitis B.





































