Applied Mathematics
Vol.06 No.06(2015), Article ID:56887,5 pages
10.4236/am.2015.66091
Introduce a Novel PCA Method for Intuitionistic Fuzzy Sets Based on Cross Entropy
Sonia Darvishi1, Adel Fatemi2, Pouya Faroughi2*
1Department of Statistics, North Tehran Branch, Islamic Azad University, Tehran, Iran
2Department of Statistics, Sanandaj Branch, Islamic Azad University, Sanandaj, Iran
Email: soniadarvishi@yahoo.com, fatemi@iausdj.ac.ir, *pouyafaroughi@iausdj.ac.ir
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 5 April 2015; accepted 1 June 2015; published 4 June 2015
ABSTRACT
In this paper, a new method for Principal Component Analysis in intuitionistic fuzzy situations has been proposed. This approach is based on cross entropy as an information index. This new method is a useful method for data reduction for situations in which data are not exact. The inexactness in the situations assumed here is due to fuzziness and missing data information, so that we have two functions (membership and non-membership). Thus, method proposed here is suitable for Atanasov’s Intuitionistic Fuzzy Sets (A-IFSs) in which we have an uncertainty due to a mixture of fuzziness and missing data information. For the demonstration of the application of the method, we have used an example and have presented a conclusion.
Keywords:
PCA, Cross Entropy, Intuitionistic Fuzzy Sets, Discrimination Information Measure, A-IFSs

1. Introduction
This study can be very significant for statistical analyzes, since in many situations of data collection not only the data are recorded inexactly, but also they might be incomplete due to data missing. In other words, since this study applies to intuistionistic fuzzy situation, which is a generalized form of the fuzzy situation, it will have significant implications for all fuzzy situations. Intuitionistic fuzzy set [1] is a generalization of fuzzy sets [2] . Due to the significance of intuistionistic fuzzy sets as a generalized fuzzy situation, many scholars have devoted attention to the subject and have applied the results of their studies to different fields, especially statistical analysis ( [3] - [6] ).
Principal Component Analysis (PCA) is a favorite statistical method for classification and data reduction. This method is very useful in other sciences too. Szmidt and Kacprzyk introduced a PCA based on Pearson correlation for intuitionistic fuzzy sets [7] . Unlike Szmidt and Kacprzyk who used Pearson correlation, in this paper, we use cross entropy as correlation index. Since cross entropy is a correlation index as well as an information index, it can provide more information on the data that Pearson correlation. Therefore, as explained before, in the situation where there are missing data and the existing data are inexact, we need a more comprehensive index such as cross entropy. Otherwise, the results of the data analysis may be extremely removed from reality due to the simultaneous working of missing data and inexactness of data. Moreover, in researches conducted in social sciences, a respondent’s decision to leave a question unanswered is itself part of the data, but these data are usually disregarded in data analysis. In this proposed method, we use cross entropy of intuitionistic fuzzy sets in order to take into account such pieces of information and other forms of missing data. The ability to take into account those data which is usually disregarded in other methods is the main merit of this new method. Fengetal introduced a new method for PCA based on Mutual Information [8] . Their method, however, applies to crisp sets. Although they too have proved that information index is better that Pearson correlation in PCA method, their method cannot be generalized to intuitionistic fuzzy sets. Fatemi introduced a stochastic form of cross entropy for intuitionistic fuzzy sets [9] . Since PCA for intuitionistic fuzzy set based on Pearson correlation does not use all information, we can use information index instead and propose a new method as an alternative to Szmidt and Kacprzyk method.
The paper is divided into 5 main sections. In Section 2, we provide an overview of some of the basic concepts of intuitionistic fuzzy sets which are required for the present study. In Section 3, the definition of cross entropy and its characteristics will be provided. In Section 4, our novel method will be explained and demonstrated through Szmidt and Kacprzyk’s example [7] . In Section 5, the results of the study and the derived conclusion will be presented in brief.
2. Intuitionistic Fuzzy Sets
In this section, we will present those aspects of intuitionistic fuzzy sets that are necessary for our discussions. As a generalized form of fuzzy sets, intuitionistic fuzzy sets have two functions: membership function and non- membership function, so that their sum is less that 1, which means that intuitionistic fuzzy sets, unlike fuzzy sets, keeps room for hesitancy such as unanswered items in a questionnaire in social sciences. As shown here, we will use such blank spaces in questionnaires as information in our classification.
An intuitionistic fuzzy set A in reference set X is given by:
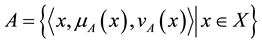 (1)
(1)
where
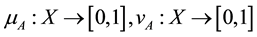 (2)
(2)
with the condition that
 (3)
(3)
and
 (4)
(4)
Denote the degree of membership and non-membership of X to A, respectively.
Obviously, each fuzzy set 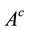 in X may be presented as the following intuitionistic fuzzy set:
in X may be presented as the following intuitionistic fuzzy set:
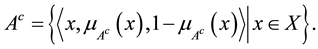 (5)
(5)
For each intuitionistic fuzzy set in X, we will call
 (6)
(6)
the intuitionistic index of x in A. It is the hesitancy degree of x to A. It is obvious that
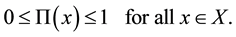 (7)
(7)
For each fuzzy set 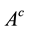 in X, evidently, we have
in X, evidently, we have
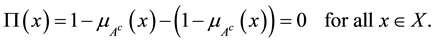 (8)
(8)
As shown above the hesitancy of the index for the intuitionistic fuzzy sets is meaningful whereas it is null for the fuzzy sets. It is for this reason that it is argued that intuitionistic fuzzy sets is more information-sensitive that fuzzy sets.
3. Cross Entropy of Intuitionistic Fuzzy Sets
In this section, we discus cross entropy for two probability distributions and in the second part we present a complete form of cross entropy for intuitionistic fuzzy sets. Information indices, such as cross entropy and mutual information, are not only information measures but also correlation measures, since they contain the characteristic of distance. The reason we preferred cross entropy over mutual information is that the latter is based on probability functions. For the same reason, mutual information has been used, by other researches, for random variables. Therefore in the next subsection we will focus on cross entropy for probability functions and, then, we will discuss it in regard to fuzzy and intuitionistic fuzzy sets.
3.1. The Cross Entropy
In information theory, the cross entropy between two probability distributions measures the average number of bits needed to identity an event from a set of possibilities if a coding is used based on a given probability distribution q rather than the “true” distribution p. Cross entropy is a measure of the divergence of two probability plans based on entropy structure.
The cross entropy for two distributions p and q over the same probability space is defined as follows:
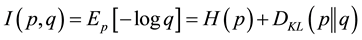 (9)
(9)
where H(p) is the entropy of p which is defined as
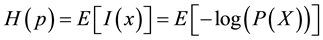 (10)
(10)
with the possible values of X being 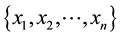 with twoprobability functions p(x) and q(x), and
with twoprobability functions p(x) and q(x), and 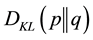 being the Kullback-Leibler divergence of q from p.
being the Kullback-Leibler divergence of q from p.
For discrete probability distributions p and q the k-l divergence of q from p is defined as
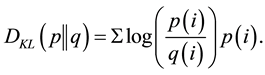 (11)
(11)
3.2. Fuzzy Cross Entropy
Regarding the similarities that exist between fuzzy membership function and probability function, Shang and Jiang defined the cross entropy for two fuzzy sets in the same reference set [10] .
Let A and B be two FSs defined on X. Then
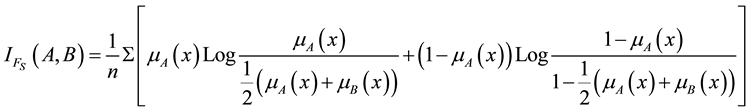 (12)
(12)
is called fuzzy cross entropy, where n is the cardinality of the finite reference set X.
3.3. Intuitionistic Fuzzy Cross Entropy
10 years after Shang and Jiang offered the first definition of fuzzy cross entropy; Valachos and Sergiadis modified and generalized the concept of fuzzy cross entropy for intuitionistic fuzzy situations.
Let A and B be two IFSs defined on X. Then

is called intuitionistic fuzzy cross entropy, where n is the cardinality of the finite reference set X.
That Formula is the degree of discrimination and divergence of A from B. However, it is not symmetric [11] .
For two IFSs A and B,

is called a symmetric discrimination information measure for IFSs. It is obviously seen that the three conditions below is satisfied. It should be noted that the definition of discrimination information measure for IFSs is due to the third condition, i.e. the condition of being symmetrical.

4. PCA for Intuitionistic Fuzzy Data Based on Cross Entropy
After the text edit has been completed, the paper is ready for the template. Duplicate the template file by using the Save As command, and use the naming convention prescribed by your journal for the name of your paper. In this newly created file, highlight all of the contents and import your prepared text file. You are now ready to style your paper.
In this section we solve an example presented in Szmidt and Kacprzyk’s paper through ours new method [7] . This well-known example which has come to be called “Saturday Morning” was first considered by Quinland [12] . We have chosen Quinland’s example since its attributes are nominal which means that we have intuitionistic fuzzy sets. We have intuitionistic fuzzy sets because we have uncertainty due to membership measures and hesitancy due to non-membership measures. This example has been used by many researches since, despite its brevity, it is illustrative and it contains all aspects of Atanasov’s Intuitionistic Fuzzy Sets (A-IFSs) (Table 1). We could have used an example from social sciences including questionnaires with unanswered items, but we preferred this example for the above reasons.
Szmidt and Kacprzyk solved it with correlation matrices [7] . At first, they computed the correlation matrices between the attributes. Then they calculated their eigenvectors and eigenvalues. In that approach to PCA Pearson correlation could measure only a linear correlation.
We recall the cross entropy to solve this problem. We begin by computing the 1-D. The results are given in Table 2. We calculate their eigenvectors and eigenvalues. Eigenvectors (Table 3) are: 0.009, 0.0002, 0.1054, 3.9028, so that the first eigenvalue explains 97% of the overall variation.
The eigenvectors for eigenvalue are given in Tables 3-5.
5. Conclusion
As we saw, based on the four attributes that were four Atanassov’s intuitionistic fuzzy sets, we managed to obtain the symmetrical form of their cross entropy that formed a matrix showing the divergence of the four A-IFSs. Then we used 1-enteries of the matrix, because we were interested in correlation not divergence. Based on the matrix we obtained the eigenvectors and eigenvalues, with the eigenvectors forming the components of the matrix. And, based on the eigenvalues we obtained the amount of the variation of the data and through that we sorted the components. As you see in Table 5, which is the final result of our research, the first (the main) component controls 97% of the variation. Since for data collection we used A-IFSs and for the demonstration of the correlation we used cross entropy, our analysis can be more detailed and exact. Finally, based on our data and our approach, we presented a new method to PCA for intuitionistic fuzzy sets based on cross entropy. Since IFSs also cover all forms of FSs, introducing the new PCA method for IFSs is a valuable work. In this paper,
Table 1. The “Saturday Morning” data in terms of the A-IFSs).
Table 2. Symmetric discrimination information measure of the “Saturday Morning” data.
Table 3. Eigenvalues of the 1-symmetric discrimination information.
Table 4. Eigenvectors for eigenvalues.
Table 5. Principle components and their eigenvalue percentages.
we have replaced cross entropy as an information index for Pearson correlation, and we have tried to improve the method.
References
- Atanassov, K.T. (1983) Intuitionistic Fuzzy Sets. Fuzzy Sets and Systems, 20, 87-96. http://dx.doi.org/10.1016/S0165-0114(86)80034-3
- Zadeh, L.A. (1965) Fuzzy Sets. Information and Control, 8, 338-353. http://dx.doi.org/10.1016/S0019-9958(65)90241-X
- Li, D.-F. (2014) Multiattribute Decision-Making Methods with Intuitionistic Fuzzy Sets. In: Decision and Game Theory in Management with Intuitionistic Fuzzy Sets, 308, 75-151. http://dx.doi.org/10.1007/978-3-642-40712-3_3
- Li, D.-F. (2014) Multiattribute Group Decision-Making Methods with Intuitionistic Fuzzy Sets. In: Decision and Game Theory in Management with Intuitionistic Fuzzy Sets, 308, 251-288. http://dx.doi.org/10.1007/978-3-642-40712-3_6
- Szmidt, E., Kacprzyk, J. and Bujnowski, P. (2013) The Kendall Rank Correlation between Intuitionistic Fuzzy Sets: An Extended Analysis. Soft Computing: State of the Art Theory and Novel Applications, 291, 39-54. http://dx.doi.org/10.1007/978-3-642-34922-5_4
- Zhang, X., Deng, Y., Chan, F.T.S., Xu, P., Mahadevan, S. and Hu, Y. (2013) IFSJSP: A Novel Methodology for the Job-Shop Scheduling Problem Based on Intuitionistic Fuzzy Sets. International Journal of Production Research, 51, 5100-5119. http://dx.doi.org/10.1080/00207543.2013.793425
- Szmidt, E. and Kacprzyk, J. (2012) A New Approach to Principal Component Analysis for Intuitionistic Fuzzy Data Sets. Advances in Computational Intelligence. Communications in Computer and Information Science, 298, 529-538.
- Feng, H., Yuan, M. and Fan, X. (2012) PCA Based on Mutual Information for Acoustic Environment Classification. Paper Presented at the International Conference on Audio, Language and Image Processing (ICALIP), Shanghai Ac- oustics Laboratory, Shanghai, 16-18.
- Fatemi, A. (2011) Entropy of Stochastic Intuitionistic Fuzzy Sets. Journal of Applied Sciences, 11, 748-751. http://dx.doi.org/10.3923/jas.2011.748.751
- Shang, X.G. and Jiang, W.S. (1997) A Note on Fuzzy Information Measures. Pattern Recognition Letters, 18, 425-432. http://dx.doi.org/10.1016/S0167-8655(97)00028-7
- Valchos, I.K. and Sergiadis, G.D. (2007) Intuitionistic Fuzzy Information―Applications to Pattern Recognition. Pattern Recognition Letters, 28, 197-206. http://dx.doi.org/10.1016/j.patrec.2006.07.004
- Quinland, J.R. (1986) Induction of Decisions Trees. Machine Learning, 1, 81-106. http://dx.doi.org/10.1007/BF00116251
NOTES
*Corresponding author.





